Bio-Info每日一题:Rosalind-07-Mendel‘s First Law(孟德尔第一定律 python实现)
🎉 进入生物信息学的世界,与Rosalind一起探索吧!🧬
Rosalind是一个在线平台,专为学习和实践生物信息学而设计。该平台提供了一系列循序渐进的编程挑战,帮助用户从基础到高级掌握生物信息学知识。无论你是初学者还是专业人士,Rosalind都能为你提供适合的学习资源和实践机会。网址:https://rosalind.info
你是否想像专业人士一样分析DNA序列?这里有一个简单的任务来帮助你入门。
📝 任务说明:

这个题目是要你计算在一群具有不同基因型的个体中,两两随机交配后,后代中表现显性性状的概率。题目给出了三种基因型的个体数量:
- k: 纯合显性个体的数量(homozygous dominant, AA)
- m: 杂合个体的数量(heterozygous, Aa)
- n: 纯合隐性个体的数量(homozygous recessive, aa)
需要计算两两随机选取个体交配后,后代表现显性性状(具有显性等位基因)的概率。
解答
可能的配对及其概率:
-
AA×AA:总是产生 AA(100% 显性)
-
AA×Aa(或 Aa×AA):产生 50% AA 和 50% Aa(100% 显性)
-
AA×aa(或 aa×AA):总是产生 Aa(100% 显性)
-
Aa×Aa:产生 25% AA、50% Aa 和 25% aa(75% 显性)
-
Aa×aa(或 aa×Aa):产生 50% Aa 和 50% aa(50% 显性)
-
aa×aa:总是产生 aa(0% 显性)
每种配对的概率计算

-
计算最终的概率:
- 最终的概率是上述每种配对概率与其产生显性表型概率的乘积之和。
def dominant_phenotype_probability(k, m, n):# 总个体数total = k + m + n# 各种配对产生显性表型的概率prob_AA_AA = (k / total) * ((k - 1) / (total - 1))prob_AA_Aa = 2 * (k / total) * (m / (total - 1))prob_AA_aa = 2 * (k / total) * (n / (total - 1))prob_Aa_Aa = (m / total) * ((m - 1) / (total - 1))prob_Aa_aa = 2 * (m / total) * (n / (total - 1))prob_aa_aa = (n / total) * ((n - 1) / (total - 1))# 显性表型的总概率probability = (prob_AA_AA * 1 +prob_AA_Aa * 1 +prob_AA_aa * 1 +prob_Aa_Aa * 0.75 +prob_Aa_aa * 0.5 +prob_aa_aa * 0)return probabilitydef main():# 从输入读取数据k = int(input("请输入显性纯合体(AA)的个体数: "))m = int(input("请输入杂合体(Aa)的个体数: "))n = int(input("请输入隐性纯合体(aa)的个体数: "))# 计算并打印概率result = dominant_phenotype_probability(k, m, n)print(f"产生显性表型后代的概率: {result:.5f}")if __name__ == "__main__":main()补充
孟德尔第一定律,也称为分离律(Law of Segregation),是孟德尔在研究豌豆遗传实验时发现的基本遗传定律之一。该定律描述了在生殖细胞形成过程中,等位基因如何分离并在后代中重新组合的现象。具体内容如下:
-
等位基因分离:每个个体有一对等位基因控制某一特定性状(例如豌豆的颜色),这些等位基因在生殖细胞(配子)形成时会分离。每个配子只会携带其中一个等位基因。
-
随机组合:受精时,来自父本和母本的配子随机结合,从而形成新的基因型。这意味着后代的基因型是随机组合的,具有不同的等位基因组合。
孟德尔通过研究豌豆的性状,如花的颜色和种子的形状,发现了这种分离现象。具体来说,他注意到当他交配纯合显性个体和纯合隐性个体时,第一代子代(F1代)全部表现出显性性状,而第二代子代(F2代)则按3:1的比例分离出显性和隐性性状。
以下是对孟德尔第一定律的简要总结:
- 每个性状由一对等位基因控制。
- 在形成配子时,等位基因分离,每个配子只包含一个等位基因。
- 受精时,来自父母双方的等位基因随机结合,决定后代的基因型和表现型。
相关文章:

Bio-Info每日一题:Rosalind-07-Mendel‘s First Law(孟德尔第一定律 python实现)
🎉 进入生物信息学的世界,与Rosalind一起探索吧!🧬 Rosalind是一个在线平台,专为学习和实践生物信息学而设计。该平台提供了一系列循序渐进的编程挑战,帮助用户从基础到高级掌握生物信息学知识。无论你是初…...

C++ 47 之 函数调用运算符重载
#include <iostream> #include <string> using namespace std;class MyPrint{ public:// 重载小括号() 重载谁operator后就紧跟谁的符号void operator()(string txt){cout << txt << endl;} };class MyAdd{ public:int operator()(int a, int b){retur…...
[Qt的学习日常]--常用控件1
前言 作者:小蜗牛向前冲 名言:我可以接受失败,但我不能接受放弃 如果觉的博主的文章还不错的话,还请点赞,收藏,关注👀支持博主。如果发现有问题的地方欢迎❀大家在评论区指正 目录 一、什么是控…...
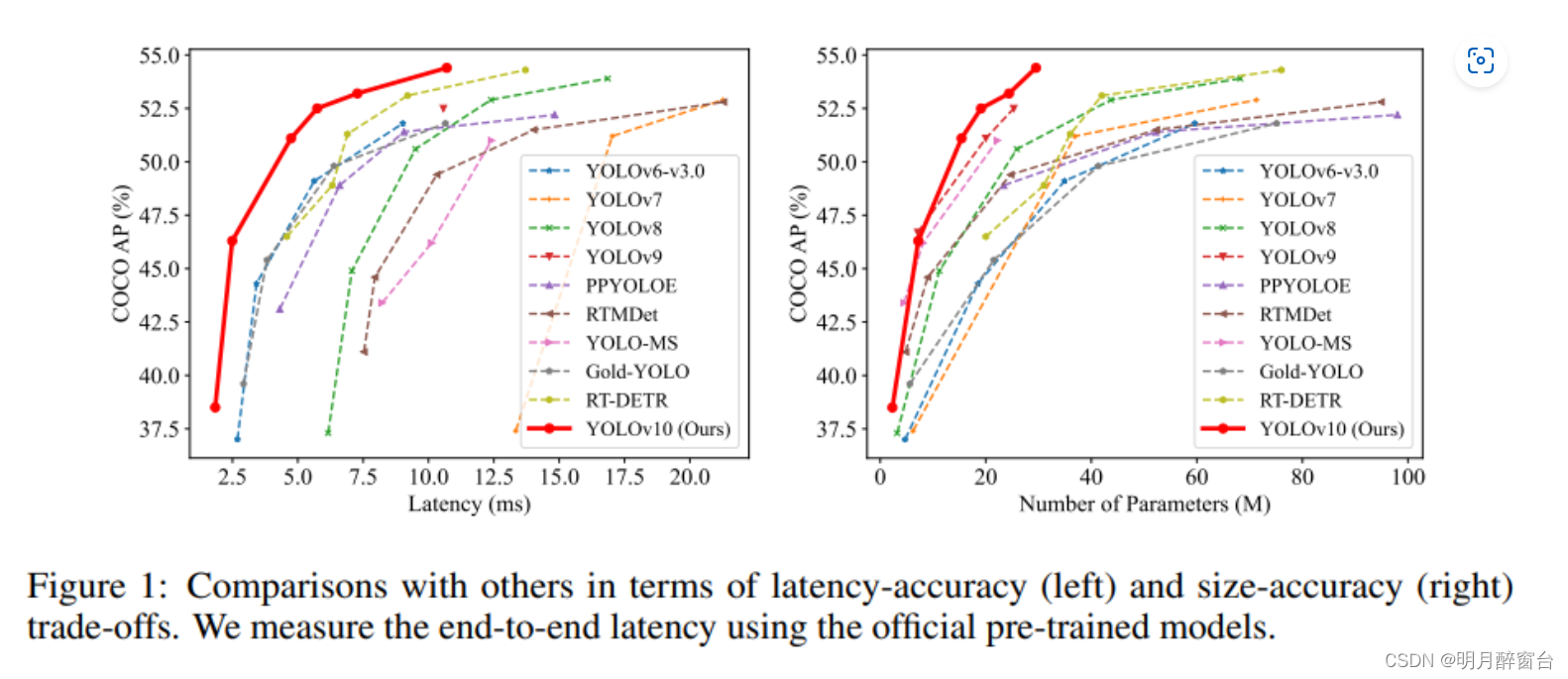
模型实战(23)之 yolov10 使用总结及训练自己的数据集
yolov10 使用总结及训练自己的数据集 0. yolov10 原理分析 此处参考:https://blog.csdn.net/CVHub/article/details/139204248论文:https://arxiv.org/pdf/2405.14458源码:https://github.com/THU-MIG/yolov10 论文原理分析: 创新: 双标签分配策略 众所周知,标签分配策略…...
AIRNet模型使用与代码分析(All-In-One Image Restoration Network)
AIRNet提出了一种较为简易的pipeline,以单一网络结构应对多种任务需求(不同类型,不同程度)。但在效果上看,ALL-In-One是不如One-By-One的,且本文方法的亮点是batch内选择patch进行对比学习。在与sota对比上…...

欧洲杯“球迷狂欢趴”开启,容声带来“健康养鲜”新理念
6月15日,容声冰箱在深圳举行了异彩纷呈的“欧洲杯养鲜补给站 球迷狂欢趴”系列活动。 容声国内营销总经理韩栋现场发布“以品质领先 为健康养鲜”的主题内容,强调容声将以健康养鲜技术产品的升级迭代,满足用户品质生活需求。 作为有着41年发…...

人工智能对零售业的影响
机器人、人工智能相关领域 news/events (专栏目录) 本文目录 一、人工智能如何改变零售格局二、利用人工智能实现购物体验自动化三、利用人工智能改善库存管理四、通过人工智能解决方案增强客户服务五、利用人工智能分析消费者行为六、利用 AI 打造个性化…...
Spring Boot + EasyExcel + SqlServer 进行批量处理数据
前言 在日常开发和工作中,我们可能要根据用户上传的文件做一系列的处理,本篇文章就以Excel表格文件为例,模拟用户上传Excel文件,讲述后端如何高效的进行数据的处理。 一.引入 EasyExcel 依赖 <!-- https://mvnrepository.com/…...
深入理解指针(四)
目录 1. 回调函数是什么? 2. qsort使用举例 2.1冒泡排序 2.2使用qsort函数排序整型数据 2.3 使用qsort排序结构数据(名字) 2.4 使用qsort排序结构数据(年龄) 3. qsort函数的模拟实现 1. 回调函数是什么? 回调函数就是⼀个通过函数指针调⽤的函数。 如果你把函数…...

k-means聚类模型的优缺点
一、k-means聚类模型的优点 1. 简单高效:k-means算法思想简单直观,易于实现。它通过迭代计算样本点与聚类中心之间的距离,并不断调整聚类中心的位置,直至满足终止条件。由于其计算过程相对直接,所以具有较高的执行效率…...
我的创作纪念日(1825天)
Ⅰ、机缘 1. 记得是大一、大二的时候就听学校的大牛说,可以通过写 CSDN 博客,来提升自己的代码和逻辑能力,虽然即将到了写作的第六个年头,但感觉这句话依旧受用; 2、今年一整年的创作都没有停止,本年度几乎是每周都来…...
Studio One 6.6.2 for Mac怎么激活,有Studio One 6激活码吗?
如果您是一名音乐制作人,您是否曾经为了寻找一个合适的音频工作站而苦恼过?Studio One 6 for Mac是一款非常适合您的MacBook的音频工作站。它可以帮助您轻松地录制、编辑、混音和发布您的音乐作品。 Studio One 6.6.2 for Mac具有直观的界面和强大的功能…...
Windows搭建nacos集群
Nacos是阿里巴巴的产品,现在是SpringCloud中的一个组件。相比Eureka功能更加丰富,在国内受欢迎程度较高。 下载地址:Tags alibaba/nacos GitHub 链接:百度网盘 请输入提取码 提取码:8888 解压文件夹 目录说明&am…...

kotlin 中的字符
一、字符类型 1、kotlin中,字符用Char类型表示,值使用单引号 括起来。 fun main() {val a: Char 1println(a) // 1println("a类型为:${a.javaClass.simpleName}") // a类型为:char } 2、特殊字符的表示。 \t——制…...

yocto根文件系统如何配置静态IP地址
在Yocto根文件系统中配置静态IP地址,你可以参考以下步骤。请注意,这些步骤可能会因Yocto版本和具体硬件平台的不同而略有差异。 1. 获取网络配置信息 首先,你需要从网络运维方获取分配的IP地址、子网掩码、默认网关和DNS信息。 2. 确定配置文…...

【博客720】时序数据库基石:LSM Tree的辅助优化
时序数据库基石:LSM Tree的辅助优化 场景: LSM Tree其实本质是一种思想,而具体是否需要WAL,内存表用什么有序数据结构来组织,磁盘上的SSTable用什么结构来存放,是否需要布隆过滤器来加快不存在数据的判断等…...
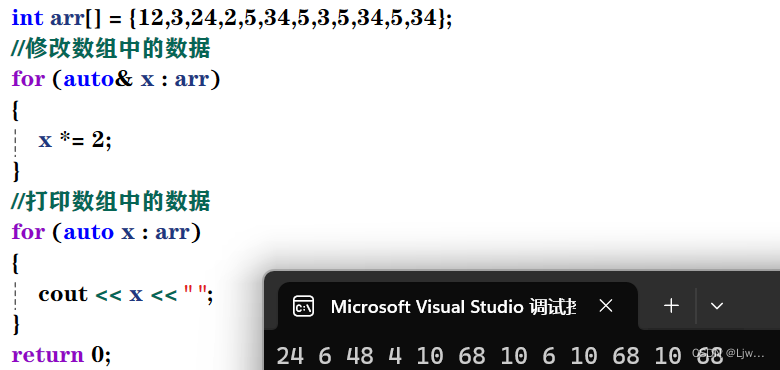
C++前期概念(重)
目录 命名空间 命名空间定义 1. 正常的命名空间定义 2. 命名空间可以嵌套 3.头文件中的合并 命名空间使用 命名空间的使用有三种方式: 1:加命名空间名称及作用域限定符(::) 2:用using将命名空间中某个成员引入 3:使用using namespa…...

Java字符串加密HMAC-SHA1密钥,转换成Base64编码
新建一个maven测试项目,直接把代码复制过去就行,把data和secretKey的值替换成想加密的值。 package test;import javax.crypto.Mac; import javax.crypto.spec.SecretKeySpec; import java.security.InvalidKeyException; import java.security.NoSuchA…...
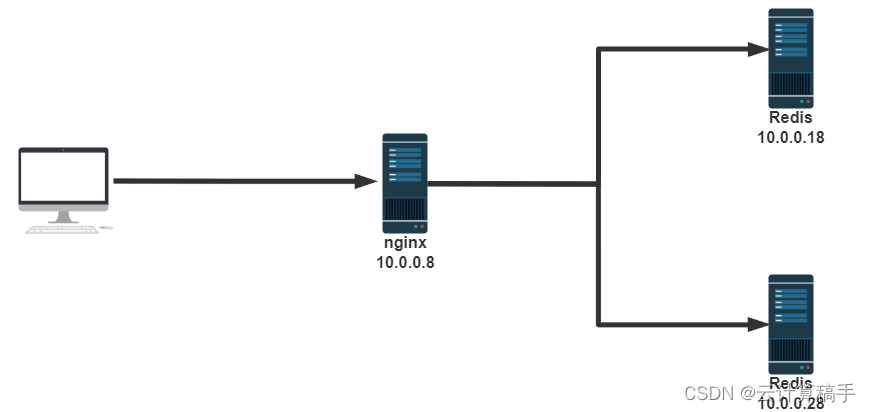
【网络架构】Nginx
目录 一、I/O模型 1.1 Linux 的 I/O 1.2 零拷贝技术 1.3 网络IO模型 1.3.1 阻塞型 I/O 模型(blocking IO)编辑 1.3.2非阻塞型 I/O 模型 (nonblocking IO)编辑 1.3.3 多路复用 I/O 型 ( I/O multiplexing )编辑 1.3.4 信号驱动式 I/O 模型 …...

C# OpenCvSharp 逻辑运算-bitwise_and、bitwise_or、bitwise_not、bitwise_xor
bitwise_and 函数 🤝 作用或原理: 将两幅图像进行与运算,通过逻辑与运算可以单独提取图像中的某些感兴趣区域。如果有掩码参数,则只计算掩码覆盖的图像区域。 示例: 在实际应用中,可以用 bitwise_and 来提取图像中的某些部分。例如,我们可以从图像中提取出一个特定的颜…...

地震勘探——干扰波识别、井中地震时距曲线特点
目录 干扰波识别反射波地震勘探的干扰波 井中地震时距曲线特点 干扰波识别 有效波:可以用来解决所提出的地质任务的波;干扰波:所有妨碍辨认、追踪有效波的其他波。 地震勘探中,有效波和干扰波是相对的。例如,在反射波…...

SkyWalking 10.2.0 SWCK 配置过程
SkyWalking 10.2.0 & SWCK 配置过程 skywalking oap-server & ui 使用Docker安装在K8S集群以外,K8S集群中的微服务使用initContainer按命名空间将skywalking-java-agent注入到业务容器中。 SWCK有整套的解决方案,全安装在K8S群集中。 具体可参…...

安宝特方案丨XRSOP人员作业标准化管理平台:AR智慧点检验收套件
在选煤厂、化工厂、钢铁厂等过程生产型企业,其生产设备的运行效率和非计划停机对工业制造效益有较大影响。 随着企业自动化和智能化建设的推进,需提前预防假检、错检、漏检,推动智慧生产运维系统数据的流动和现场赋能应用。同时,…...

1.3 VSCode安装与环境配置
进入网址Visual Studio Code - Code Editing. Redefined下载.deb文件,然后打开终端,进入下载文件夹,键入命令 sudo dpkg -i code_1.100.3-1748872405_amd64.deb 在终端键入命令code即启动vscode 需要安装插件列表 1.Chinese简化 2.ros …...

JDK 17 新特性
#JDK 17 新特性 /**************** 文本块 *****************/ python/scala中早就支持,不稀奇 String json “”" { “name”: “Java”, “version”: 17 } “”"; /**************** Switch 语句 -> 表达式 *****************/ 挺好的ÿ…...

Spring AI与Spring Modulith核心技术解析
Spring AI核心架构解析 Spring AI(https://spring.io/projects/spring-ai)作为Spring生态中的AI集成框架,其核心设计理念是通过模块化架构降低AI应用的开发复杂度。与Python生态中的LangChain/LlamaIndex等工具类似,但特别为多语…...

基于Springboot+Vue的办公管理系统
角色: 管理员、员工 技术: 后端: SpringBoot, Vue2, MySQL, Mybatis-Plus 前端: Vue2, Element-UI, Axios, Echarts, Vue-Router 核心功能: 该办公管理系统是一个综合性的企业内部管理平台,旨在提升企业运营效率和员工管理水…...

Spring AI Chat Memory 实战指南:Local 与 JDBC 存储集成
一个面向 Java 开发者的 Sring-Ai 示例工程项目,该项目是一个 Spring AI 快速入门的样例工程项目,旨在通过一些小的案例展示 Spring AI 框架的核心功能和使用方法。 项目采用模块化设计,每个模块都专注于特定的功能领域,便于学习和…...

中科院1区顶刊|IF14+:多组学MR联合单细胞时空分析,锁定心血管代谢疾病的免疫治疗新靶点
中科院1区顶刊|IF14:多组学MR联合单细胞时空分析,锁定心血管代谢疾病的免疫治疗新靶点 当下,免疫与代谢性疾病的关联研究已成为生命科学领域的前沿热点。随着研究的深入,我们愈发清晰地认识到免疫系统与代谢系统之间存在着极为复…...

十二、【ESP32全栈开发指南: IDF开发环境下cJSON使用】
一、JSON简介 JSON(JavaScript Object Notation)是一种轻量级的数据交换格式,具有以下核心特性: 完全独立于编程语言的文本格式易于人阅读和编写易于机器解析和生成基于ECMAScript标准子集 1.1 JSON语法规则 {"name"…...
