稀疏矩阵是什么 如何求
稀疏矩阵是一种特殊类型的矩阵,其中大多数元素都是零。由于稀疏矩阵中非零元素的数量远少于零元素,因此可以使用特定的数据结构和算法来高效地存储和处理它们,从而节省存储空间和计算时间。

RowPtr 数组中的每个元素表示对应行的第一个非零元素在 Values 数组中的位置。最后一个元素表示整个 Values 数组的长度,用来标识矩阵的结束位置。
这个矩阵中非零元素只有 5 个,其余元素都是零,因此这个矩阵可以被认为是稀疏矩阵。
存储方法:
为了节省空间,稀疏矩阵常用以下几种常见的存储方法:
-
压缩行存储(Compressed Row Storage, CRS):
用三个一维数组来存储稀疏矩阵:
Values:存储非零元素的值。Column:存储对应非零元素的列索引。RowPtr:存储每一行的起始位置在Values数组中的索引。
例如,对于上面的矩阵 A:
Values存储所有的非零元素[3, 22, 17, 8, 6]。Column存储每个非零元素所在的列[2, 0, 4, 2, 1]。RowPtr存储每行第一个非零元素在Values中的索引[0, 1, 3, 3, 4, 5]。其中最后一个值 5 是用来标识最后一行的结束位置。
-
压缩列存储(Compressed Column Storage, CCS):
这个方法类似于 CRS,但按列存储:
Values:存储非零元素的值。Row:存储对应非零元素的行索引。ColPtr:存储每一列的起始位置在Values数组中的索引。
应用场景:
稀疏矩阵广泛应用于以下领域:
- 科学计算:如有限元分析、计算流体力学等。
- 机器学习:如推荐系统中的用户-物品矩阵。
- 图论:如图的邻接矩阵表示。
使用稀疏矩阵的特定存储方法和算法可以大大提高计算的效率和节省存储空间。
如何构建稀疏矩阵存储
Step 1: Values 和 Column 数组
先确定 Values 和 Column 数组:
-
第一行:非零元素是 3,位置在第 3 列
Values = [3]Column = [2]
-
第二行:非零元素是 22 和 17,位置分别在第 1 列和第 5 列
Values = [3, 22, 17]Column = [2, 0, 4]
-
第三行:没有非零元素
Values和Column数组保持不变Values = [3, 22, 17]Column = [2, 0, 4]
-
第四行:非零元素是 8,位置在第 3 列
Values = [3, 22, 17, 8]Column = [2, 0, 4, 2]
-
第五行:非零元素是 6,位置在第 2 列
Values = [3, 22, 17, 8, 6]Column = [2, 0, 4, 2, 1]
Step 2: RowPtr 数组
计算每行的起始位置:
- 第一行:第一个非零元素在
Values的位置是 0,因此RowPtr[0] = 0 - 第二行:第一个非零元素在
Values的位置是 1,因此RowPtr[1] = 1 - 第三行:没有非零元素,
RowPtr[2]应该和前一行的结束位置相同(第二行的结束位置是RowPtr[1] + 第二行的非零元素个数 = 1 + 2 = 3) - 第四行:第一个非零元素在
Values的位置是 3,因此RowPtr[3] = 3 - 第五行:第一个非零元素在
Values的位置是 4,因此RowPtr[4] = 4 - 结束位置:
Values数组的长度是 5,所以RowPtr[5] = 5
最终的存储数组
Values = [3, 22, 17, 8, 6]Column = [2, 0, 4, 2, 1]RowPtr = [0, 1, 3, 3, 4, 5]
解释每个值
RowPtr[0] = 0:第一行第一个非零元素在Values中的位置是 0RowPtr[1] = 1:第二行第一个非零元素在Values中的位置是 1RowPtr[2] = 3:第三行没有非零元素,起始位置和前一行的结束位置相同RowPtr[3] = 3:第四行第一个非零元素在Values中的位置是 3RowPtr[4] = 4:第五行第一个非零元素在Values中的位置是 4RowPtr[5] = 5:表示整个矩阵的非零元素结束的位置(即Values数组的长度)
通过这种方式,RowPtr 数组帮助我们快速定位每一行在 Values 数组中的起始和结束位置,从而方便对稀疏矩阵进行高效操作。希望这样解释能帮助你更好地理解 RowPtr 数组的构建方法。
相关文章:

稀疏矩阵是什么 如何求
稀疏矩阵是一种特殊类型的矩阵,其中大多数元素都是零。由于稀疏矩阵中非零元素的数量远少于零元素,因此可以使用特定的数据结构和算法来高效地存储和处理它们,从而节省存储空间和计算时间。 RowPtr 数组中的每个元素表示对应行的第一个非零元…...
 -- SOCKET : Unix domain)
57.Linux/Unix 系统编程手册(下) -- SOCKET : Unix domain
https://blog.51cto.com/u_15567199/5204540 【linux网络编程】容错处理文件 wrap.h、wrap.c_wx623c6c9. // 容错处理 wrap.h #ifndef _WRAP_H_ #define _WRAP_H_#include <stdio.h> #include <stdlib.h> #include <unistd.h> #include <error.h> #i…...
Hvv--知攻善防应急响应靶机--Linux1
HW–应急响应靶机–Linux1 所有靶机均来自 知攻善防实验室 靶机整理: 夸克网盘:https://pan.quark.cn/s/4b6dffd0c51a#/list/share百度云盘:https://pan.baidu.com/s/1NnrS5asrS1Pw6LUbexewuA?pwdtxmy 官方WP:https://mp.weixin.…...

Solus Linux: 有自己的软件包管理器
Solus Linux 是一个独立的 Linux 发行版,它以简单易用和现代化的用户体验而著称。Solus Linux 使用的包管理器是 eopkg,它具有以下优势和特点: 用户友好的界面:eopkg 提供了一个简洁直观的命令行界面,使得用户可以轻松…...

Java GUI编程
引言 图形用户界面(GUI)编程是使应用程序与用户进行交互的重要部分。Java提供了多种用于GUI开发的工具和库,最常用的是Swing和AWT。本文将详细介绍Java GUI编程的基础知识,包括Swing和AWT框架、事件处理以及高级GUI组件的使用&…...

ROS机器人小车建模仿真与SLAM
文章目录 一、URDF二、创建小车模型1.创建功能包2.导入依赖3.创建urdf,launch文件:4.可视化 三、添加雷达1.xacro文件2.集成和修改launch3.添加摄像头和雷达 三.GAZEBO仿真四、orbslam2kitti1.下载2.安装编译ORB_SLAM23.运行Kitee数据集 一、URDF URDFÿ…...
Windows10安装Docker Desktop(实操步骤版)
1,下载Docker Desktop 官网下载地址: https://desktop.docker.com/win/stable/amd64/Docker%20Desktop%20Installer.exe 国内镜像下载地址(本人下载这个): https://smartidedl.blob.core.chinacloudapi.cn/docker/2…...
)
Leetcode 45. 跳跃游戏 II(DP 双指针)
Leetcode 45. 跳跃游戏 II 动态规划 使用dp [ ] 记录每个位置可达的最小步数,每到达一个点时,更新该点所能跳跃区间内的所有点的dp值 时间复杂度较高 class Solution {public int jump(int[] nums) {int n nums.length;int dp[] new int [n];int N …...
(实时更新))
Codeforces Round 952 (Div. 4)(实时更新)
A - Creating Words 题意:略 代码: #include<bits/stdc.h> #define ios ios::sync_with_stdio(0),cin.tie(0),cout.tie(0)//不能使用scanf了 #define int long long #define loop(n) for(int i0;i<n;i) #define rloop(n) for(int in-1;i>…...
【AI实践】Dify开发应用和对接微信
自定义应用 创建应用有2种, 从应用模板创建 空白应用,也就是自定义应用 选择翻译助手 Translation assistant模板创建一个应用 自定义应用,创建一个child_accompany_bot自定的应用,用来支持家长,如何解决低龄儿童的…...

精准定位,智慧提纯:高级数据提取策略
在数据驱动的时代,高级数据提取策略成为企业决策、科学研究以及各类项目成功的关键。数据提取,不仅仅是简单地收集信息,而是需要精准定位目标数据,并通过智慧提纯方法,从海量数据中提取出有价值、有深度的信息。本文将…...

USB转I2C转SPI芯片CH341与CH347比较
1. 芯片中文资料: USB转I2C转SPI芯片CH341 高速USB转接芯片CH347转9M双串口转I2C转SPI转JTAG转SWD USB2.0高速转接芯片CH347应用开发手册 2. CH341与CH347比较: 类别CH341CH347备注串口速度2M9MCH347的串口速度更快设置CH341的I2C或SPI不能与串口同…...
举例以及期权无套利定价公式)
期权无风险套利(Risk-Free Arbitrage)举例以及期权无套利定价公式
期权市场的无风险套利 中文版 期权市场中的套利实例 为了清楚地说明,让我们通过一个现实的例子来展示套利。 期权市场中的套利实例 假设市场上有以下价格: 标的股票价格:100美元欧式看涨期权(行权价100美元,3个月…...
)
Java基础知识巩固自测(上)
前言 该文章适用于已初步了解Java基础知识的入门学习者,便于快速回顾知识点,查漏补缺。 内容包括:Java面向对象相关知识、SQL基础语法 复习建议技巧 实用3W思维法(What、Why、How) 1. What(什么&#x…...
通过 Python+Nacos实现微服务,细解微服务架构
shigen坚持更新文章的博客写手,擅长Java、python、vue、shell等编程语言和各种应用程序、脚本的开发。记录成长,分享认知,留住感动。 个人IP:shigen 背景 一直以来的想法比较多,然后就用Python编写各种代码脚本。很多…...

如何使用new和delete操作符进行动态内存分配和释放?
在C中,new 和 delete 操作符用于在堆(heap)上动态地分配和释放内存。这是管理内存的一种重要方式,特别是在需要创建可变数量或生命周期与程序执行流程不一致的对象时。 使用 new 进行动态内存分配 当你使用 new 操作符时&#x…...

【SCAU数据挖掘】数据挖掘期末总复习题库选择题及解析
1.将原始数据进行集成、变换、维度规约、数值规约是在以下哪个步骤的任务?( C ) A.频繁模式挖掘 B.分类和预测 C.数据预处理 D.数据流挖掘 解析:数据预处理是数据分析和数据挖掘的重要步骤之一,包括数据清洗、集成、变换、规约(如维度规约、数值规约)等。这…...
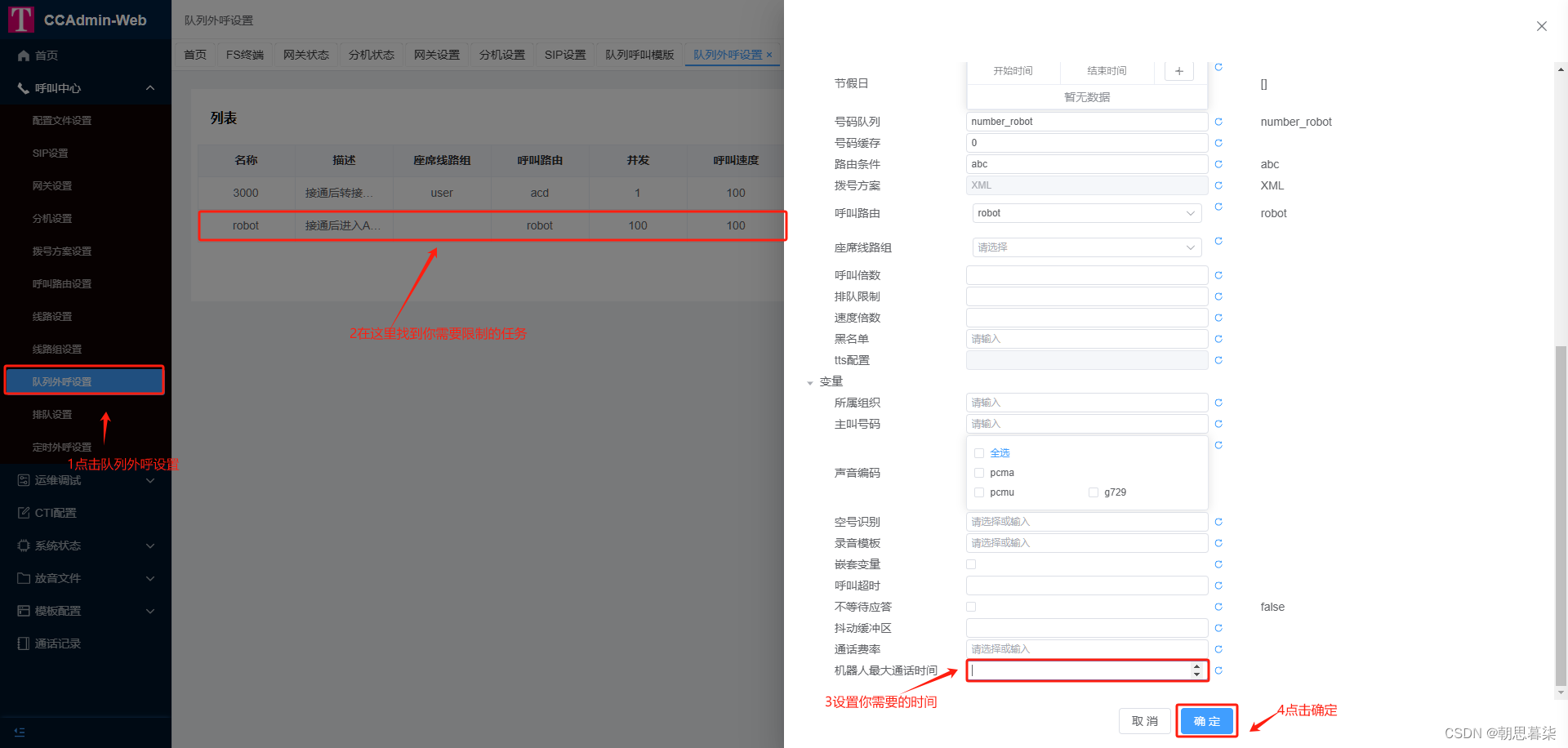
顶顶通呼叫中心中间件-限制最大通话时间(mod_cti基于FreeSWITCH)
顶顶通呼叫中心中间件-限制最大通话时间(mod_cti基于FreeSWITCH) 一、最大通话时间 1、配置拨号方案 1、点击拨号方案 ->2、在框中输入通话最大时长->3、点击添加->4、根据图中配置->5、勾选continue。修改拨号方案需要等待一分钟即可生效 action"sched…...

深度学习:使用argparse 模块
在深度学习中,结合 Bash 脚本和 argparse 模块,可以实现高效的任务自动化和参数管理。Bash 脚本可以用来调度任务和管理环境,而 argparse 模块可以用来解析命令行参数,控制深度学习模型的训练和评估过程。 1.argparse 模块 argp…...

unity text根据文本内容自动设置高度
我们经常会遇到需要根据文字数量动态修改文本框高度的需求,我们可以使用文本的行数*每行的高度来计算文本框的高度,伪代码如下: int oneLineHight 50;// 每行的像素高度 private void ResetTextHight(string str) {//设置文字内容ShowText.…...

网络编程(Modbus进阶)
思维导图 Modbus RTU(先学一点理论) 概念 Modbus RTU 是工业自动化领域 最广泛应用的串行通信协议,由 Modicon 公司(现施耐德电气)于 1979 年推出。它以 高效率、强健性、易实现的特点成为工业控制系统的通信标准。 包…...

Android Wi-Fi 连接失败日志分析
1. Android wifi 关键日志总结 (1) Wi-Fi 断开 (CTRL-EVENT-DISCONNECTED reason3) 日志相关部分: 06-05 10:48:40.987 943 943 I wpa_supplicant: wlan0: CTRL-EVENT-DISCONNECTED bssid44:9b:c1:57:a8:90 reason3 locally_generated1解析: CTR…...

多模态2025:技术路线“神仙打架”,视频生成冲上云霄
文|魏琳华 编|王一粟 一场大会,聚集了中国多模态大模型的“半壁江山”。 智源大会2025为期两天的论坛中,汇集了学界、创业公司和大厂等三方的热门选手,关于多模态的集中讨论达到了前所未有的热度。其中,…...

【Java学习笔记】Arrays类
Arrays 类 1. 导入包:import java.util.Arrays 2. 常用方法一览表 方法描述Arrays.toString()返回数组的字符串形式Arrays.sort()排序(自然排序和定制排序)Arrays.binarySearch()通过二分搜索法进行查找(前提:数组是…...

华为云Flexus+DeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建
华为云FlexusDeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建 前言 如今大模型其性能出色,华为云 ModelArts Studio_MaaS大模型即服务平台华为云内置了大模型,能助力我们轻松驾驭 DeepSeek-V3/R1,本文中将分享如何…...

大学生职业发展与就业创业指导教学评价
这里是引用 作为软工2203/2204班的学生,我们非常感谢您在《大学生职业发展与就业创业指导》课程中的悉心教导。这门课程对我们即将面临实习和就业的工科学生来说至关重要,而您认真负责的教学态度,让课程的每一部分都充满了实用价值。 尤其让我…...

基于matlab策略迭代和值迭代法的动态规划
经典的基于策略迭代和值迭代法的动态规划matlab代码,实现机器人的最优运输 Dynamic-Programming-master/Environment.pdf , 104724 Dynamic-Programming-master/README.md , 506 Dynamic-Programming-master/generalizedPolicyIteration.m , 1970 Dynamic-Programm…...

USB Over IP专用硬件的5个特点
USB over IP技术通过将USB协议数据封装在标准TCP/IP网络数据包中,从根本上改变了USB连接。这允许客户端通过局域网或广域网远程访问和控制物理连接到服务器的USB设备(如专用硬件设备),从而消除了直接物理连接的需要。USB over IP的…...

Spring是如何解决Bean的循环依赖:三级缓存机制
1、什么是 Bean 的循环依赖 在 Spring框架中,Bean 的循环依赖是指多个 Bean 之间互相持有对方引用,形成闭环依赖关系的现象。 多个 Bean 的依赖关系构成环形链路,例如: 双向依赖:Bean A 依赖 Bean B,同时 Bean B 也依赖 Bean A(A↔B)。链条循环: Bean A → Bean…...

基于TurtleBot3在Gazebo地图实现机器人远程控制
1. TurtleBot3环境配置 # 下载TurtleBot3核心包 mkdir -p ~/catkin_ws/src cd ~/catkin_ws/src git clone -b noetic-devel https://github.com/ROBOTIS-GIT/turtlebot3.git git clone -b noetic https://github.com/ROBOTIS-GIT/turtlebot3_msgs.git git clone -b noetic-dev…...
