Java数据结构与算法(0/1背包问题)
前言:
背包问题(Knapsack Problem)是组合优化问题中的一个经典问题,有多个变种。这里我们讨论的是 0/1 背包问题,这是最基本的一种形式。问题的描述如下:
给定 n 件物品,每件物品有一个重量 wi 和一个价值 vi,以及一个背包,它能够承载的最大重量为 W。我们需要确定应该将哪些物品放入背包,以使得背包内物品的总价值最大。
背包问题分类:
- 0-1背包问题
- 完全背包问题
- 多重背包问题
- 混合背包问题
- 二维背包问题
- 分组背包问题
- 有依赖的背包问题 (困难)
解题思路:
使用动态规划可以有效地解决 0/1 背包问题。动态规划的思想是将问题分解成子问题,并利用子问题的解来构建原问题的解。
- 定义状态:用 dp[i][j]表示前 i件物品恰好放入一个容量为 j的背包时所能获得的最大价值。
- 状态转移方程:
- 如果不选第 i件物品:dp[i][j]=dp[i−1][j]
- 如果选第 i件物品:dp[i][j]=dp[i−1][j−wi]+vi
- 综上:dp[i][j]=max(dp[i−1][j],dp[i−1][j−wi]+vi)
- 初始条件:dp[0][j]=0对于所有的 j,即没有物品时的最大价值为 0。
实现代码
public class Knapsack {public static int knapsack(int W, int[] weights, int[] values, int n) {int[][] dp = new int[n + 1][W + 1];for (int i = 1; i <= n; i++) {for (int w = 0; w <= W; w++) {if (weights[i - 1] <= w) {dp[i][w] = Math.max(dp[i - 1][w], dp[i - 1][w - weights[i - 1]] + values[i - 1]);} else {dp[i][w] = dp[i - 1][w];}}}return dp[n][W];}public static void main(String[] args) {int W = 50; // 背包容量int[] weights = {10, 20, 30}; // 物品重量int[] values = {60, 100, 120}; // 物品价值int n = values.length;System.out.println("最大价值: " + knapsack(W, weights, values, n));}
}
QA1:
相关文章:
)
Java数据结构与算法(0/1背包问题)
前言: 背包问题(Knapsack Problem)是组合优化问题中的一个经典问题,有多个变种。这里我们讨论的是 0/1 背包问题,这是最基本的一种形式。问题的描述如下: 给定 n 件物品,每件物品有一个重量 wi 和一个价值…...
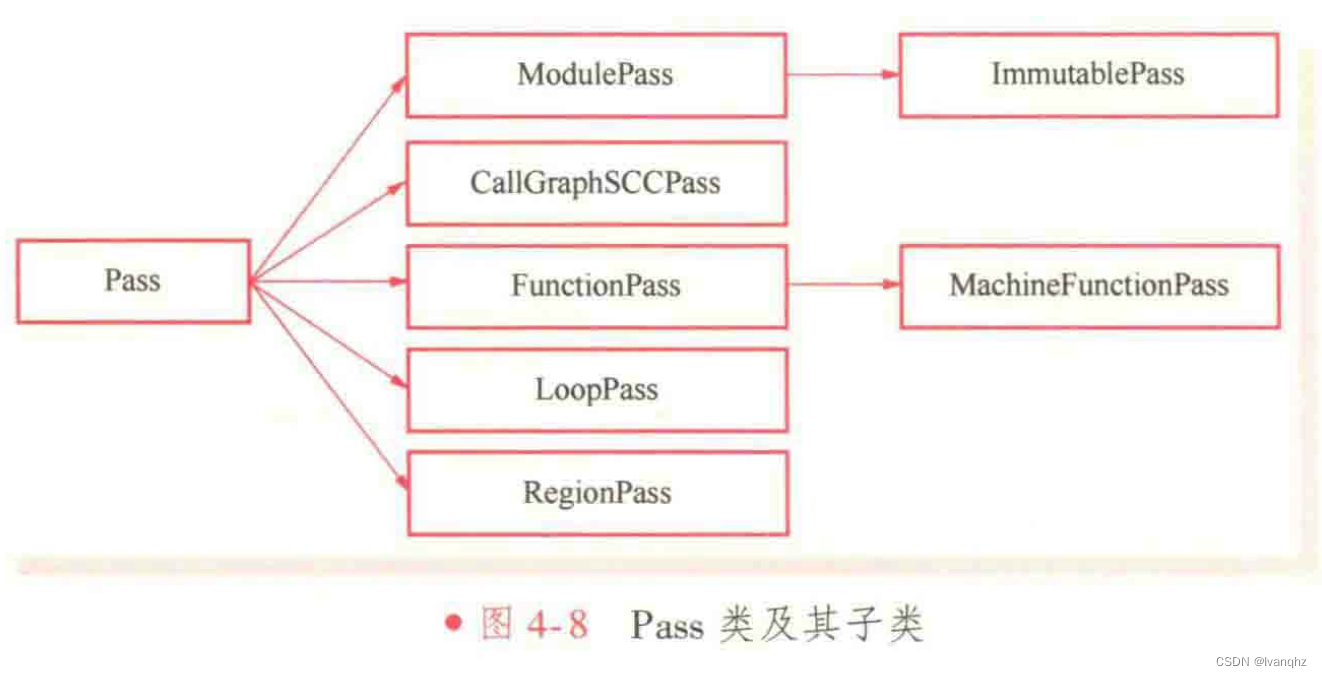
LLVM 中 的 pass 及其管理机制
概述 LLVM 编译器框架的核心概念是任务调用和执行 编译器开发者将IR分解为不同的处理对象,并将其处理过程实现为单独的pass类型。在编译器初始化,pass被实例化,并被添加到pass管理中 pass 管理器(pass manager) 以流水线的方式将各个独立的…...

第 5 章 监控系统 | 入门案例 - 虚拟机监控
👉 本文目标:为 Linux 虚拟机/服务器安装 node_exporter,实现对虚拟机/服务器的监控。 👀 本文内容: 安装 Node Exporter,暴露 Linux 指标(比如 CPU、磁盘、IO 等)配置 Prometheus 抓取 Node Exporter 暴露的指标数据配置 Recording Rule,便于缓存/加速 Dashboard 频…...

教资认定报名照片要求小于190kb…
教资认定报名照片要求小于190kb…… 要求:文件小于190kb,宽度290-300,高度408-418 方法:vx搜随时照-教资认定 直接制作合规尺寸即可,还可以打印纸质版邮寄到家...

显示类控件——Calendar Widget
🐌博主主页:🐌倔强的大蜗牛🐌 📚专栏分类:QT ❤️感谢大家点赞👍收藏⭐评论✍️ 文章目录 一、Calendar Widget介绍核心属性重要信号代码示例: 获取选中的日期 一、Calendar Widget 介绍 …...
system与excel族函数区别
1.system #include<stdlib.h> int system(const char *command); comand是命令的路径,一般我们用绝对路径 system函数会创建新的进程,新的进程执行完返回原来的进程,原来的进程则继续执行后面的代码段。 如我们创建一个sys.cpp文件…...
STM32存储左右互搏 模拟U盘桥接SPI总线FATS读写FLASH W25QXX
STM32存储左右互搏 模拟U盘桥接SPI总线FATS读写FLASH W25QXX STM32的USB接口可以模拟成为U盘,通过FATS文件系统对连接的存储单元进行U盘方式的读写。 这里介绍STM32CUBEIDE开发平台HAL库模拟U盘桥接SPI总线FATS读写W25Q各型号FLASH的例程。 FLASH是常用的一种非易失…...
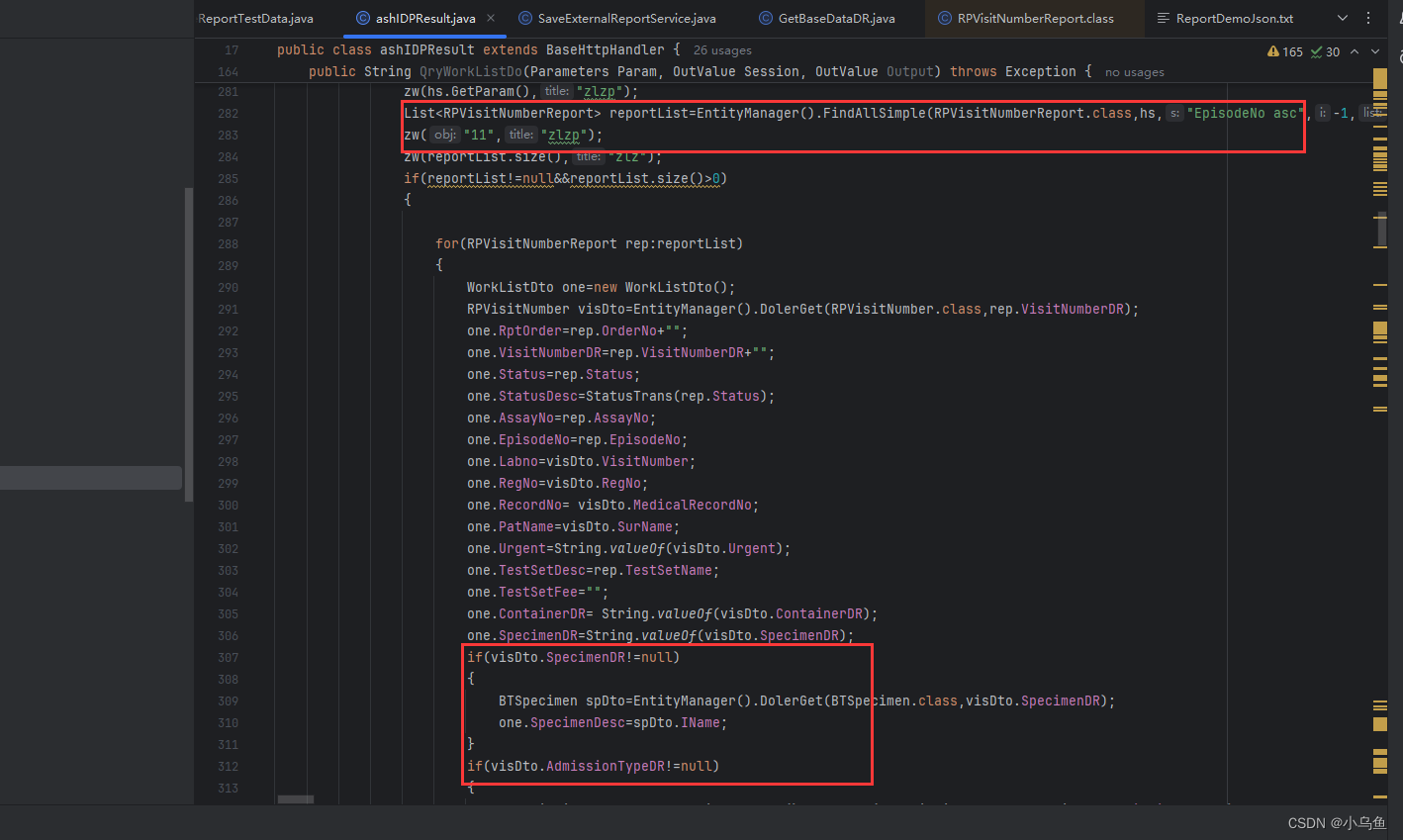
jrt从量变到质变
又是一个加班的周末,上周把台式机代码和数据库环境弄好了,这周进行大数据测试,直接把标本、标本医嘱、报告、报告结果、药敏结果等数据插入到1亿的规模,跑了一天一夜插入了5000多万个标本,后面接着补剩下的到一亿。 演…...

NLP主流大模型如GPT3/chatGPT/T5/PaLM/LLaMA/GLM的原理和差异有哪些-详细解读
自然语言处理(NLP)领域的多个大型语言模型(如GPT-3、ChatGPT、T5、PaLM、LLaMA和GLM)在结构和功能上有显著差异。以下是对这些模型的原理和差异的深入分析: GPT-3 (Generative Pre-trained Transformer 3) 虽然GPT-4…...

从MySQL到NoSQL:分析传统关系型数据库与NoSQL数据库的协同
引言 数据库是一个系统,用来管理和存储数据的地方。数据在数据库中以一种结构化的方式组织,这样能更容易地查询和处理数据。 关系型数据库是基于关系模型的数据库,它将数据存储在不同的表中,每个表都有各自的独一无二的主键。表与表之间通过共享的数据项相互关联。像MySQ…...

三、树和割集
文章目录 1、树1.1 树的定义1.2 树的性质1.3 极小连通图1.4 树的中心1.5 生成树1.5.1 最小生成树 2、 割点和桥THE END 1、树 1.1 树的定义 \qquad 定义: 一个连通的无圈的图称为树。 \qquad 只有一个顶点的树叫做平凡树。 \qquad 树中度为1的节点称为叶子结点。…...
中的类型)
泛型中<>和()中的类型
尖括号 < > 中的类型参数定义了一组可以被替换的类型占位符,而圆括号 (...) 内的类型使用则是这些类型参数的具体应用场景,展示了这些类型变量如何参与到函数的参数和返回值类型定义中去。这样设计既保证了代码的灵活性,又保持了类型安…...
)
spark mllib 特征学习笔记 (一)
PySpark MLlib 特征处理详解 PySpark MLlib 提供了丰富的特征处理工具,帮助我们进行特征提取、转换和选择。以下是 PySpark MLlib 中常用的特征处理类及其简要介绍。 1. Binarizer Binarizer 是将连续特征二值化的转换器。 from pyspark.ml.feature import Bina…...

SQLite 日期 时间
SQLite 日期 & 时间 SQLite 是一种轻量级的数据库管理系统,广泛用于各种应用程序中。它支持标准的 SQL 语法,包括对日期和时间的处理。在 SQLite 中,日期和时间可以通过几种不同的方式来存储和操作。 日期和时间数据类型 SQLite 使用 …...

飞书API 2-1:如何通过 API 创建文件夹?
本文探讨如何通过飞书的 API 来创建文件夹。通过 API 创建的文件夹,一般是放在共享空间,如果要放在个人空间,建议手动创建。 查看 API 文档 API 路径,可在飞书开放平台的服务端 API,依次查找云文档>云空间>文件…...
【APP移动端自动化测试】第一节.环境配置和adb调试工具
文章目录 前言一、Java环境搭建二、AndroidSDK环境搭建三、Android模拟器安装四、adb调试工具基本介绍 4.1 adb构成和基本原理 4.2 adb获取包名,界面名 4.3 adb文件传输 4.4 adb获取app启动时间 4.5 adb获取手机日志 4.6 adb其他有关…...

Kotlin 协程:从基础概念到开发实践
前言 上一篇文章 深入理解Android多线程开发:场景应用与解决方案解析 针对Android开发中的多线程应用场景和相应的解决方案做了一个梳理。 总结出了Android开发中多线程编程的几个重要点: 资源复用和优化切线程任务编排并结合示例说明了Kotlin协程在处理上述问题时的优势。 …...

IPNV6
特征——升级点: 1、全球单播地址 ----IPV4地址下的公有地址 V6下没 nat 2、可聚合性 (IANA组织对全球的地址进行合理分配) 3、多宿主——一个物理接口可以同时拥有多个不同网段的IPV6地址;但不同接口不能在同一网段 4、自动配置 1ÿ…...

C++并发之锁(std::lock_guard,std::unique_lock)
目录 1 概述2 使用实例3 接口使用3.1 lock_guard3.2 adopt_lock3.3 defer_lock3.4 try_to_lock3.5 try_lock3.6 release3.7 lock3.8 call_one1 概述 锁保护是通过使互斥对象始终处于锁定状态来管理互斥对象的对象。。 在构造时,互斥对象被调用线程锁定,在析构时,互斥被解…...

FreeRTOS队列(queue)
队列(queue)可以用于"任务到任务"、 "任务到中断"、 "中断到任务"直接传输信息。 1、队列的特性 1、1常规操作 队列的简化操如下图所示,从此图可知: 队列中可以包含若干数据:队列中有若干项,这…...

Vim 调用外部命令学习笔记
Vim 外部命令集成完全指南 文章目录 Vim 外部命令集成完全指南核心概念理解命令语法解析语法对比 常用外部命令详解文本排序与去重文本筛选与搜索高级 grep 搜索技巧文本替换与编辑字符处理高级文本处理编程语言处理其他实用命令 范围操作示例指定行范围处理复合命令示例 实用技…...
)
云计算——弹性云计算器(ECS)
弹性云服务器:ECS 概述 云计算重构了ICT系统,云计算平台厂商推出使得厂家能够主要关注应用管理而非平台管理的云平台,包含如下主要概念。 ECS(Elastic Cloud Server):即弹性云服务器,是云计算…...

【人工智能】神经网络的优化器optimizer(二):Adagrad自适应学习率优化器
一.自适应梯度算法Adagrad概述 Adagrad(Adaptive Gradient Algorithm)是一种自适应学习率的优化算法,由Duchi等人在2011年提出。其核心思想是针对不同参数自动调整学习率,适合处理稀疏数据和不同参数梯度差异较大的场景。Adagrad通…...

R语言AI模型部署方案:精准离线运行详解
R语言AI模型部署方案:精准离线运行详解 一、项目概述 本文将构建一个完整的R语言AI部署解决方案,实现鸢尾花分类模型的训练、保存、离线部署和预测功能。核心特点: 100%离线运行能力自包含环境依赖生产级错误处理跨平台兼容性模型版本管理# 文件结构说明 Iris_AI_Deployme…...

云启出海,智联未来|阿里云网络「企业出海」系列客户沙龙上海站圆满落地
借阿里云中企出海大会的东风,以**「云启出海,智联未来|打造安全可靠的出海云网络引擎」为主题的阿里云企业出海客户沙龙云网络&安全专场于5.28日下午在上海顺利举办,现场吸引了来自携程、小红书、米哈游、哔哩哔哩、波克城市、…...

如何在看板中体现优先级变化
在看板中有效体现优先级变化的关键措施包括:采用颜色或标签标识优先级、设置任务排序规则、使用独立的优先级列或泳道、结合自动化规则同步优先级变化、建立定期的优先级审查流程。其中,设置任务排序规则尤其重要,因为它让看板视觉上直观地体…...

P3 QT项目----记事本(3.8)
3.8 记事本项目总结 项目源码 1.main.cpp #include "widget.h" #include <QApplication> int main(int argc, char *argv[]) {QApplication a(argc, argv);Widget w;w.show();return a.exec(); } 2.widget.cpp #include "widget.h" #include &q…...

Mac软件卸载指南,简单易懂!
刚和Adobe分手,它却总在Library里给你写"回忆录"?卸载的Final Cut Pro像电子幽灵般阴魂不散?总是会有残留文件,别慌!这份Mac软件卸载指南,将用最硬核的方式教你"数字分手术"࿰…...

网络编程(UDP编程)
思维导图 UDP基础编程(单播) 1.流程图 服务器:短信的接收方 创建套接字 (socket)-----------------------------------------》有手机指定网络信息-----------------------------------------------》有号码绑定套接字 (bind)--------------…...

LeetCode - 199. 二叉树的右视图
题目 199. 二叉树的右视图 - 力扣(LeetCode) 思路 右视图是指从树的右侧看,对于每一层,只能看到该层最右边的节点。实现思路是: 使用深度优先搜索(DFS)按照"根-右-左"的顺序遍历树记录每个节点的深度对于…...
