三、树和割集
文章目录
- 1、树
- 1.1 树的定义
- 1.2 树的性质
- 1.3 极小连通图
- 1.4 树的中心
- 1.5 生成树
- 1.5.1 最小生成树
- 2、 割点和桥
- THE END
1、树
1.1 树的定义
\qquad 定义: 一个连通的无圈的图称为树。
\qquad 只有一个顶点的树叫做平凡树。
\qquad 树中度为1的节点称为叶子结点。
\qquad 推论1: 非平凡树中至少有两个叶子结点。
\qquad 推论2: 树是双图。
\qquad 定义: 一个无圈的图称为森林。
1.2 树的性质
\qquad 定理1: 设 G = ( V , E ) G=(V, E) G=(V,E)是一个 ( p , q ) (p,q) (p,q)图,则下列命题是等价的:
- G G G是树
- G G G中任意两个顶点之间有唯一的一条路
- G G G是连通的,且 p = q + 1 p=q+1 p=q+1
- G G G中无圈,且 p = q + 1 p=q+1 p=q+1
- G G G中无圈, G G G中任意两个不相邻的顶点之间加一条边,则得到一个有唯一圈的图
\qquad 要证明上述定理成立,需要证明任意两个结论之间互为充分必要条件,则可以将5条结论围成一圈,依次证明前一条结论是后一条结论的充要条件即可。在证明第二条到第三条的结论时,可以使用数学归纳法进行证明。证明第三条到第四条结论,从第四条结论到第一条结论和从第五条结论到第一条结论时,可以使用反证法进行证明。
1.3 极小连通图
\qquad 定义: 去掉一条边就不连通的连通图叫做极小连通图。
\qquad 定理: G G G是树的充要条件为 G G G是极小连通图。
1.4 树的中心
\qquad 偏心率: 给定一个树 G = ( V , E ) G=(V,E) G=(V,E),和任意一个 v ∈ V v \in V v∈V,定义节点 v v v的偏心率为 e ( v ) = m a x u ∈ V { d ( u , v ) } e(v)=max_{u \in V}\{d(u,v)\} e(v)=maxu∈V{d(u,v)}。
\qquad 树的半径: 树中所有顶点的最小偏心率为树的半径, r ( G ) = m i n v ∈ V { e ( v ) } r(G)=min_{v \in V}\{e(v)\} r(G)=minv∈V{e(v)}。
\qquad 树的中心: 树的中心表示为一个节点集合 H = { v ∣ v ∈ V , e ( v ) = r ( v ) } H=\{v|v \in V, e(v)=r(v)\} H={v∣v∈V,e(v)=r(v)}。
1.5 生成树
\qquad 给定一个图 G = ( V , E ) G=(V,E) G=(V,E), 若 G G G的一个生成子图是树,则称其为 G G G的生成树。
\qquad 图 G = ( V , E ) G=(V,E) G=(V,E)生成树存在的充要条件: G G G是连通图。
\qquad 给定一个图 G = ( V , E ) G=(V,E) G=(V,E)是一个 ( p , q ) (p,q) (p,q)图, G G G中至多有 p p − 2 p^{p-2} pp−2个生成树(上界)。
1.5.1 最小生成树
\qquad 对于一个图 G = ( V , E ) G=(V,E) G=(V,E)中所有的生成树,其中权值最小的生成树叫做最小生成树,求最小生成树的两个算法如下:
\qquad Prime 算法随机从图中选择一个顶点加入到最小生成树树集合中,之后选择和最小生成树集合中已经存在的顶点相邻接的其他顶点中边权值最下的顶点添加到最小生成树集合中(在此过程中判断是否有圈存在,排除生成圈的顶点),直到所有的顶点都检查完毕,其算法复杂度为 O ( p 2 ) O(p^2) O(p2)。
\qquad Kryscal 算法: 将图中所有的边按照权值进行从小到大排序,依次向生成树集合中添加权值最小的边,每添加一条边需要判断是否有圈产生,跳过有圈生成的边,直到所有的边均检查完毕为止,算法复杂度为 O ( q ∗ l o g q ) O(q*log\ q) O(q∗log q)。
2、 割点和桥
\qquad 割点定义: 给定一个图 G = ( V , E ) G=(V,E) G=(V,E), v ∈ V v \in V v∈V,假如 G − v G-v G−v的分支数大于 G G G的分支数,则称 v v v为 G G G的一个割点。
\qquad 每一个非平凡的图中至少有两个顶点不是割点(从最长路来证明)。哈密顿图中一定没有割点,从哈密顿图的定义来证明,哈密顿图中一定有哈密顿回路。
\qquad 定理1(割点的特征性质): 给定一个图 G = ( V , E ) G=(V,E) G=(V,E), v ∈ V v \in V v∈V,则下述命题等价:
- v v v是割点
- ∃ u , v ∈ V , u ≠ w \exist u, v \in V, u \neq w ∃u,v∈V,u=w, u u u和 v v v之间的所有的路均通过 v v v.
- ∃ V / { v } \exist V /\ \{v\} ∃V/ {v}的一个划分 { U , W } \{U, W\} {U,W},使得 ∀ u ∈ U , ∀ v ∈ V \forall u \in U, \forall v \in V ∀u∈U,∀v∈V, u , v u, v u,v之间的路均通过 v v v
\qquad 桥定义: 给定一个图 G = ( V , E ) G=(V,E) G=(V,E), x ∈ E x \in E x∈E,假如 G − x G-x G−x的分支数大于 G G G的分支数,则称 x x x为 G G G的一个桥。
\qquad 定理1(桥的特征性质): 给定一个图 G = ( V , E ) G=(V,E) G=(V,E), x ∈ E x \in E x∈E,则下述命题等价:
- x x x是桥
- ∃ u , v ∈ V , u ≠ w \exist u, v \in V, u \neq w ∃u,v∈V,u=w, u u u和 v v v之间的所有的路均通过 x x x.
- ∃ E / { x } \exist E /\ \{x\} ∃E/ {x}的一个划分 { U , W } \{U, W\} {U,W},使得 ∀ u ∈ U , ∀ v ∈ V \forall u \in U, \forall v \in V ∀u∈U,∀v∈V, u , v u, v u,v之间的路均通过 x x x
- x x x不在任何圈上
THE END
相关文章:

三、树和割集
文章目录 1、树1.1 树的定义1.2 树的性质1.3 极小连通图1.4 树的中心1.5 生成树1.5.1 最小生成树 2、 割点和桥THE END 1、树 1.1 树的定义 \qquad 定义: 一个连通的无圈的图称为树。 \qquad 只有一个顶点的树叫做平凡树。 \qquad 树中度为1的节点称为叶子结点。…...
中的类型)
泛型中<>和()中的类型
尖括号 < > 中的类型参数定义了一组可以被替换的类型占位符,而圆括号 (...) 内的类型使用则是这些类型参数的具体应用场景,展示了这些类型变量如何参与到函数的参数和返回值类型定义中去。这样设计既保证了代码的灵活性,又保持了类型安…...
)
spark mllib 特征学习笔记 (一)
PySpark MLlib 特征处理详解 PySpark MLlib 提供了丰富的特征处理工具,帮助我们进行特征提取、转换和选择。以下是 PySpark MLlib 中常用的特征处理类及其简要介绍。 1. Binarizer Binarizer 是将连续特征二值化的转换器。 from pyspark.ml.feature import Bina…...

SQLite 日期 时间
SQLite 日期 & 时间 SQLite 是一种轻量级的数据库管理系统,广泛用于各种应用程序中。它支持标准的 SQL 语法,包括对日期和时间的处理。在 SQLite 中,日期和时间可以通过几种不同的方式来存储和操作。 日期和时间数据类型 SQLite 使用 …...

飞书API 2-1:如何通过 API 创建文件夹?
本文探讨如何通过飞书的 API 来创建文件夹。通过 API 创建的文件夹,一般是放在共享空间,如果要放在个人空间,建议手动创建。 查看 API 文档 API 路径,可在飞书开放平台的服务端 API,依次查找云文档>云空间>文件…...
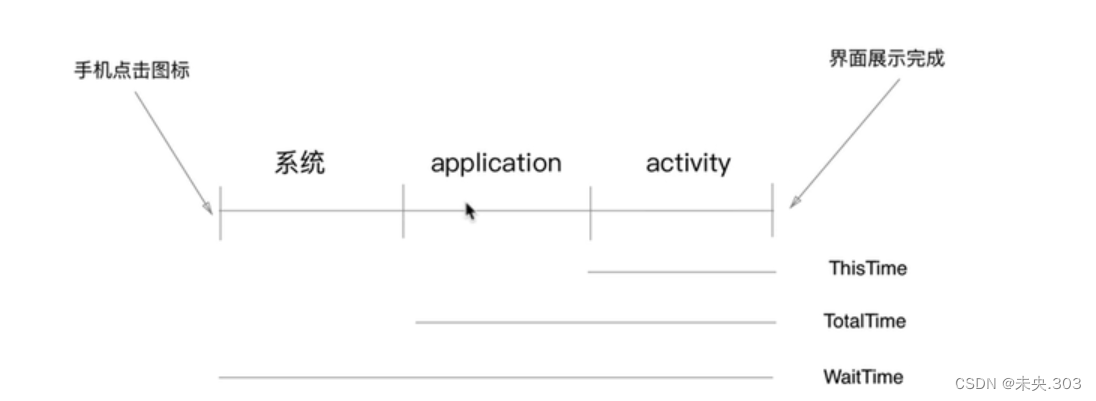
【APP移动端自动化测试】第一节.环境配置和adb调试工具
文章目录 前言一、Java环境搭建二、AndroidSDK环境搭建三、Android模拟器安装四、adb调试工具基本介绍 4.1 adb构成和基本原理 4.2 adb获取包名,界面名 4.3 adb文件传输 4.4 adb获取app启动时间 4.5 adb获取手机日志 4.6 adb其他有关…...

Kotlin 协程:从基础概念到开发实践
前言 上一篇文章 深入理解Android多线程开发:场景应用与解决方案解析 针对Android开发中的多线程应用场景和相应的解决方案做了一个梳理。 总结出了Android开发中多线程编程的几个重要点: 资源复用和优化切线程任务编排并结合示例说明了Kotlin协程在处理上述问题时的优势。 …...

IPNV6
特征——升级点: 1、全球单播地址 ----IPV4地址下的公有地址 V6下没 nat 2、可聚合性 (IANA组织对全球的地址进行合理分配) 3、多宿主——一个物理接口可以同时拥有多个不同网段的IPV6地址;但不同接口不能在同一网段 4、自动配置 1ÿ…...

C++并发之锁(std::lock_guard,std::unique_lock)
目录 1 概述2 使用实例3 接口使用3.1 lock_guard3.2 adopt_lock3.3 defer_lock3.4 try_to_lock3.5 try_lock3.6 release3.7 lock3.8 call_one1 概述 锁保护是通过使互斥对象始终处于锁定状态来管理互斥对象的对象。。 在构造时,互斥对象被调用线程锁定,在析构时,互斥被解…...

FreeRTOS队列(queue)
队列(queue)可以用于"任务到任务"、 "任务到中断"、 "中断到任务"直接传输信息。 1、队列的特性 1、1常规操作 队列的简化操如下图所示,从此图可知: 队列中可以包含若干数据:队列中有若干项,这…...
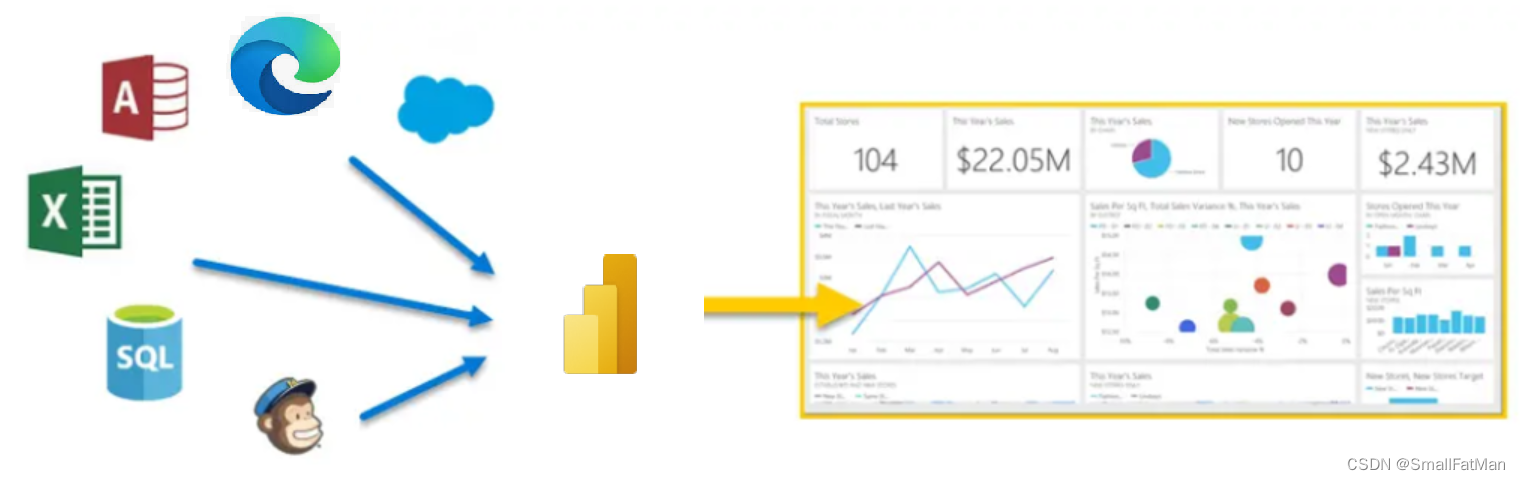
Azure数据分析Power BI
Azure数据分析Power BI 一、Power BI简介二、Power BI 如何匹配角色三、Power BI 构建基块四、使用 Power BI 服务一、Power BI简介 Microsoft Power BI 是一系列的软件服务、应用和连接器,这些软件服务、应用和连接器协同工作,将不相关的数据源转化为合乎逻辑、视觉上逼真的…...

将 Python3 程序打包成 APK 并运行在 ARM 的 Android 系统中
作为一个开发者,我们经常需要将我们的 Python 程序部署到移动端,以便更好地服务于用户。然而,直接在 Android 系统上运行 Python 程序却存在一定的挑战,因为 Android 系统默认不支持 Python。这篇文章将介绍如何将 Python3 程序打…...
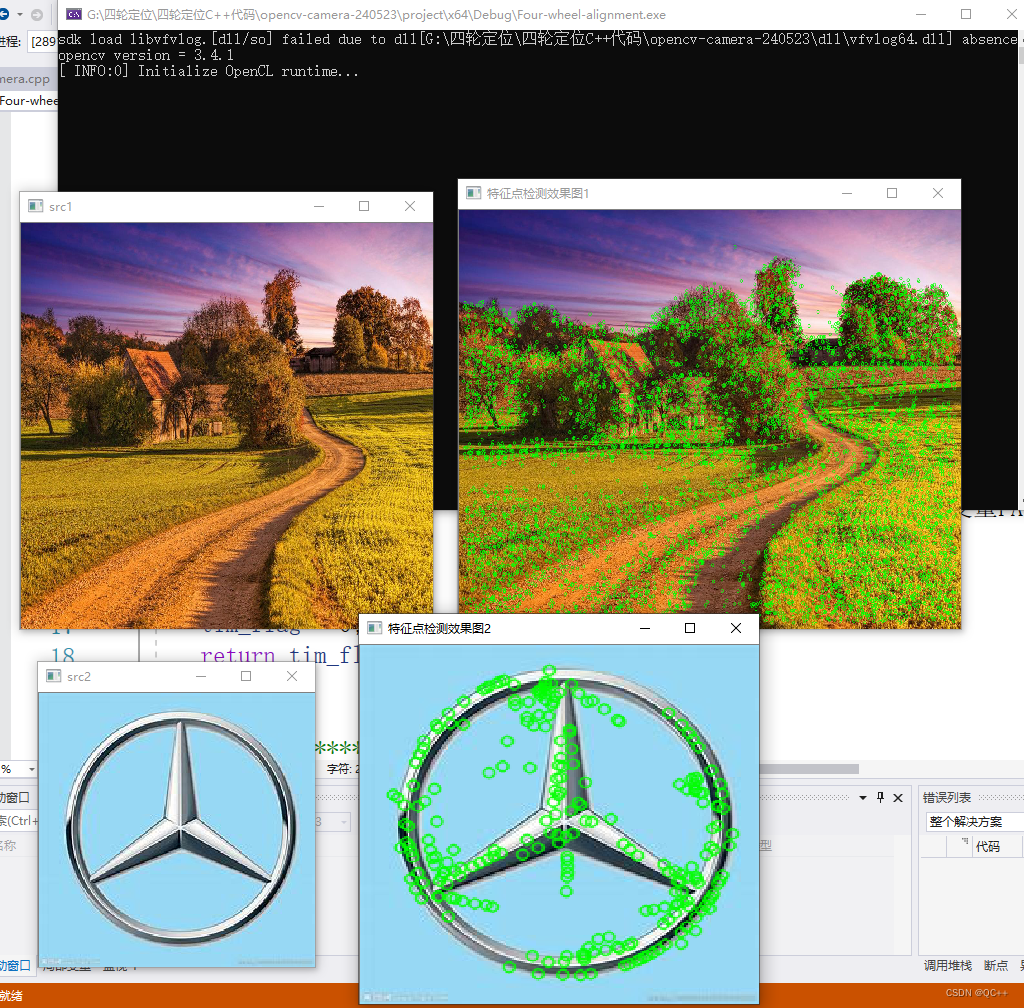
学习记录:VS2019+OpenCV3.4.1实现SURF库函数的调用
最近在学习opencv的使用,在参照书籍《OpenCV3编程入门》实现SURF时遇到不少问题,下面做归纳总结。 错误 LNK2019 无法解析的外部符号 “public: static struct cv::Ptr __cdecl cv::xfeatures2d::SURF::create(double,int,int,bool,bool)” (?createSUR…...
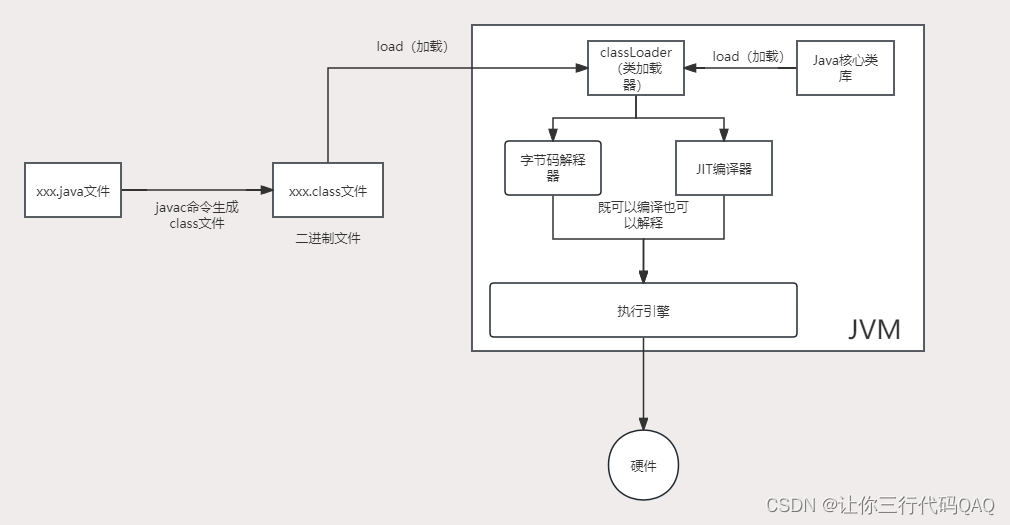
JVM-基础知识
JVM-基础知识 什么是JVM JVM是一种跨语言的平台,任何语言只要能编译成.class文件都可以被JVM运行。JVM只和.class文件有关系,和Java语言没关系。JVM是一种虚拟机规范。 java文件是如何交给JVM执行的 JVM的常见实现 HostStop:Oracle官方另外还有IBM的J9、…...

保密工作应党而生、伴党而行、为党而兴
1.(C )工作应党而生、伴党而行、为党而兴,始终是党和国家的一项重要工作。 A. 农业 B. 国防 C. 保密 D. 文化 2.机关、单位对所产生的国家秘密事项,应当按照国家秘密及其密级的具体范围的规定确定密级,同时确定&#x…...

docker login 报错: http: server gave HTTP response to HTTPS client
环境: 自建 Harbor、Docker 1. 问题分析 # 命令,这里用的是 IP,可以为域名 docker login -u test 172.16.51.182:31120 # 输入密码 Password:# 报错如下: Error response from daemon: Get "https://172.16.51.182:31120/…...

「C系列」C 文件读写
文章目录 一、C 文件读写1. 打开文件2. 写入文件3. 读取文件4. 关闭文件5. 文件读写模式6. 错误处理 二、常见问题1. 文件打开失败2. 文件读写错误3. 文件读写位置4. 缓冲区刷新 三、相关链接 一、C 文件读写 在C语言中,文件读写是通过一系列的标准库函数来完成的&…...

编程中的cos:深度解析与应用探索
编程中的cos:深度解析与应用探索 在编程的广阔天地中,cos这一数学概念扮演着举足轻重的角色。它不仅是数学函数库中的基础元素,更是图形渲染、科学计算以及数据处理等多个领域的核心工具。本文将从四个方面、五个方面、六个方面和七个方面&a…...

计算机毕业设计hadoop+spark+hive知识图谱酒店推荐系统 酒店数据分析可视化大屏 酒店爬虫 高德地图API 酒店预测系统 大数据毕业设计
流程: 1.Python爬取去哪儿网全站旅游数据约10万,存入mysql; 2.使用pandasnumpy/hadoopmapreduce对mysql中旅游数据进行数据清洗,使用高德API计算地理信息,最终转为.csv文件上传hdfs; 3.hive建库建表导入.csv文件作为数据集&#x…...

简单谈谈云服务器私网IP的存在意义及优势
云服务器是基于虚拟化技术的计算资源,可以在云平台上灵活创建和管理。为了满足不同用户的需求,云服务提供商在云服务器上分配了两种类型的IP地址:公网IP和私网IP。其中,私网IP是指在局域网内使用的内部IP地址,无法通过…...
)
椭圆曲线密码学(ECC)
一、ECC算法概述 椭圆曲线密码学(Elliptic Curve Cryptography)是基于椭圆曲线数学理论的公钥密码系统,由Neal Koblitz和Victor Miller在1985年独立提出。相比RSA,ECC在相同安全强度下密钥更短(256位ECC ≈ 3072位RSA…...

(十)学生端搭建
本次旨在将之前的已完成的部分功能进行拼装到学生端,同时完善学生端的构建。本次工作主要包括: 1.学生端整体界面布局 2.模拟考场与部分个人画像流程的串联 3.整体学生端逻辑 一、学生端 在主界面可以选择自己的用户角色 选择学生则进入学生登录界面…...
)
Spring Boot 实现流式响应(兼容 2.7.x)
在实际开发中,我们可能会遇到一些流式数据处理的场景,比如接收来自上游接口的 Server-Sent Events(SSE) 或 流式 JSON 内容,并将其原样中转给前端页面或客户端。这种情况下,传统的 RestTemplate 缓存机制会…...

大模型多显卡多服务器并行计算方法与实践指南
一、分布式训练概述 大规模语言模型的训练通常需要分布式计算技术,以解决单机资源不足的问题。分布式训练主要分为两种模式: 数据并行:将数据分片到不同设备,每个设备拥有完整的模型副本 模型并行:将模型分割到不同设备,每个设备处理部分模型计算 现代大模型训练通常结合…...

MySQL中【正则表达式】用法
MySQL 中正则表达式通过 REGEXP 或 RLIKE 操作符实现(两者等价),用于在 WHERE 子句中进行复杂的字符串模式匹配。以下是核心用法和示例: 一、基础语法 SELECT column_name FROM table_name WHERE column_name REGEXP pattern; …...

深入解析C++中的extern关键字:跨文件共享变量与函数的终极指南
🚀 C extern 关键字深度解析:跨文件编程的终极指南 📅 更新时间:2025年6月5日 🏷️ 标签:C | extern关键字 | 多文件编程 | 链接与声明 | 现代C 文章目录 前言🔥一、extern 是什么?&…...

C++ Visual Studio 2017厂商给的源码没有.sln文件 易兆微芯片下载工具加开机动画下载。
1.先用Visual Studio 2017打开Yichip YC31xx loader.vcxproj,再用Visual Studio 2022打开。再保侟就有.sln文件了。 易兆微芯片下载工具加开机动画下载 ExtraDownloadFile1Info.\logo.bin|0|0|10D2000|0 MFC应用兼容CMD 在BOOL CYichipYC31xxloaderDlg::OnIni…...

使用Spring AI和MCP协议构建图片搜索服务
目录 使用Spring AI和MCP协议构建图片搜索服务 引言 技术栈概览 项目架构设计 架构图 服务端开发 1. 创建Spring Boot项目 2. 实现图片搜索工具 3. 配置传输模式 Stdio模式(本地调用) SSE模式(远程调用) 4. 注册工具提…...

LangChain知识库管理后端接口:数据库操作详解—— 构建本地知识库系统的基础《二》
这段 Python 代码是一个完整的 知识库数据库操作模块,用于对本地知识库系统中的知识库进行增删改查(CRUD)操作。它基于 SQLAlchemy ORM 框架 和一个自定义的装饰器 with_session 实现数据库会话管理。 📘 一、整体功能概述 该模块…...

MySQL 部分重点知识篇
一、数据库对象 1. 主键 定义 :主键是用于唯一标识表中每一行记录的字段或字段组合。它具有唯一性和非空性特点。 作用 :确保数据的完整性,便于数据的查询和管理。 示例 :在学生信息表中,学号可以作为主键ÿ…...
