前缀和(一维前缀和+二维前缀和)
前缀和
定义:
前缀和是指某序列的前n项和,可以把它理解为数学上的数列的前n项和,而差分可以看成前缀和的逆运算。合理的使用前缀和与差分,可以将某些复杂的问题简单化。
用途:
前缀和一般用于统计一个区间的和,为的就是可以将区间和问题的时间复杂度降低,从而节约时间
样例:
假如说我们有一个数组,数组里面有n个元素,给你m个访问,每次给你一个L和R,问你L和R这个区间内的元素的和为多少
我们首先想到的暴力解法应该是每次调用一次for循环,去遍历区间的元素,然后求和,但是这样的时间复杂度在最坏的情况下会达到O(n*m)的时间复杂度,对于大数据来说,这种肯定是要超时的,因此我们可以用到我们的前缀和
首先,我们可以用一个前缀和数组统计出现的和,pre[ i ]放的就是在 i 之前的所有数的和,每次询问,只需要输出pre[ R ] - pre[ L - 1 ]即可,时间复杂度为O(n+m),这样就大大减小的时间复杂度
因此我们可以看到前缀和在多次求解区间和问题上的优势。
一维前缀和
在一维空间内的统计十分简单,只需要设计一个一维pre数组即可
一维前缀和预处理公式
pre[i]=pre[i-1]+a[i];
区间求解公式(从L到R的区间)
pre[R]-pre[L-1]
来看例题
P8218 【深进1.例1】求区间和

题解:很标准的前缀和问题,每次询问的都是一个区间的和,那么我们直接用一维前缀和即可
#include<bits/stdc++.h>
using namespace std;
int n;
int a[100005];
int m;
int pre[100005];
int l,r;int main()
{cin>>n;for(int i=1;i<=n;i++){cin>>a[i];pre[i]=pre[i-1]+a[i];}cin>>m;for(int i=1;i<=m;i++){cin>>l>>r;cout<<pre[r]-pre[l-1]<<"\n";}return 0;
} 二维前缀和
二维前缀和的计算是基于容斥原理的,我们需要通过对矩阵面积的划分计算来的出二维前缀和的预处理公式和求和公式
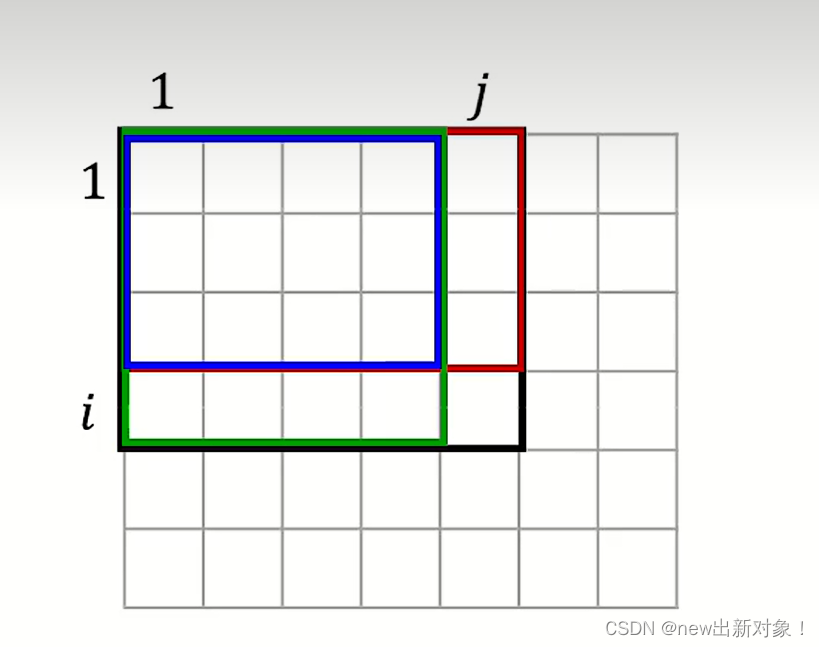
预处理公式:
我们通过这个图来了解,二维前缀和的预处理公式,首先我们将元素变成矩阵的一个一个的小方块,我们看如何去求第i行第j列之前的面积,首先我们的矩阵面积可以S(i-1,j)+S(i,j-1)的面积之和,但是多了一部分重叠部分S(i-1,j-1),并且加上额外的有下角元素a(i,j),因此我们的预处理公式就可以得出:
pre[i][j]=pre[i-1][j]+pre[i][j-1]-pre[i-1][j-1]+a[i][j];
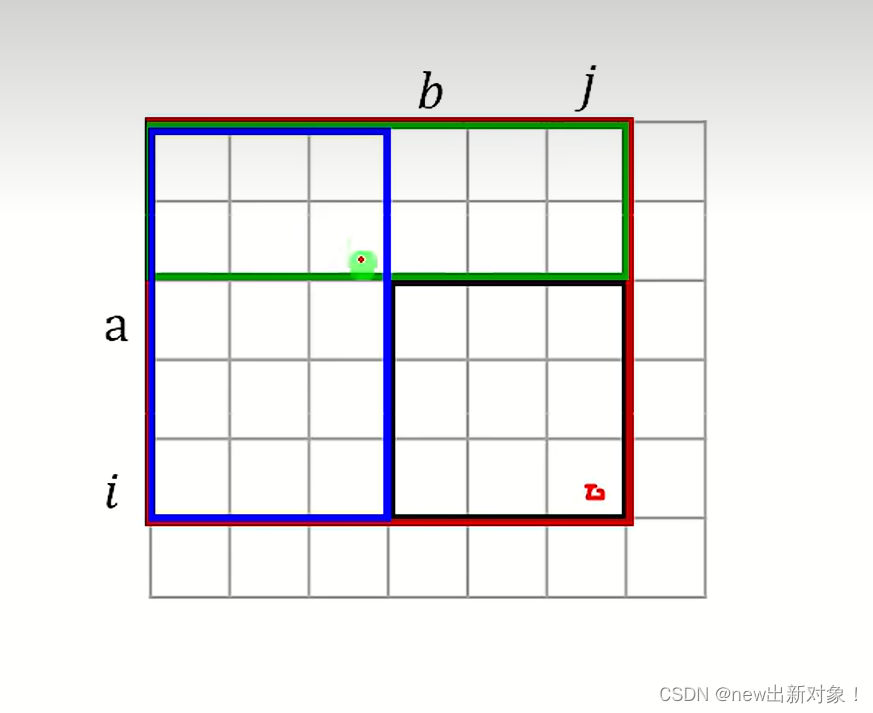
二维前缀和求和公式:
也是将计算变为矩阵面积来看,假如说我们想算从(a,b)到(i,j)的前缀和,我们首先可以用整个的大面积( S(i,j) )的面积减去S(a-1,j)和S(i,b-1),但是通过容斥原理发现我们多减一部分,那就是
S(a-1,b-1),因此我们就可以得出二维前缀和求和公式:
pre[i][j]-pre[a-1][j]-pre[i][b-1]+pre[a-1][b-1]
我们来看一道例题:最大加权矩阵

这道题,一眼就能看出来是二维前缀和,但是由于数据比较小,所以可以暴力枚举其范围,总共四重循环,计算其中前缀和的最大矩阵和,最后输出即可
#include<bits/stdc++.h>
using namespace std;int n;
int a[125][125];
int pre[125][125];signed main()
{cin>>n;for(int i=1;i<=n;i++){for(int j=1;j<=n;j++){cin>>a[i][j];pre[i][j]=pre[i-1][j]+pre[i][j-1]-pre[i-1][j-1]+a[i][j];}}int ans=-0x3f3f3f3f;for(int x1=1;x1<=n;x1++){for(int y1=1;y1<=n;y1++){for(int x2=x1;x2<=n;x2++){for(int y2=y1;y2<=n;y2++){ans=max(ans,pre[x2][y2]-pre[x1-1][y2]-pre[x2][y1-1]+pre[x1-1][y1-1]);}}}}cout<<ans;return 0;
}P2004 领地选择

题解,就是一个二维前缀和模版,很简单,直接写就OK了,只需要记录其中的左上角坐标就OK
#include<bits/stdc++.h>
using namespace std;
#define int long long
int n,m,c;
int a[1005][1005];
int pre[1005][1005];
int ans=-0x3f3f3f3f3f3f3f3f;
int x,y;signed main()
{cin>>n>>m>>c;for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){cin>>a[i][j];pre[i][j]=pre[i-1][j]+pre[i][j-1]-pre[i-1][j-1]+a[i][j];}}for(int i=c;i<=n;i++){for(int j=c;j<=m;j++){if(ans<pre[i][j]-pre[i-c][j]-pre[i][j-c]+pre[i-c][j-c]){ans=pre[i][j]-pre[i-c][j]-pre[i][j-c]+pre[i-c][j-c];x=i;y=j;}}}cout<<x-c+1<<" "<<y-c+1;return 0;
}
前缀和的应用(包括二分思想,这里默认各位看官老爷都会)
P1314 [NOIP2011 提高组] 聪明的质监员

 题意:就是说给你n个矿石,然后,这n个矿石都有自己的重量w,以及其价值v,我们有一种判断机制,就是说给你m个区间范围,每次给你一个左边界L和右边界R,我们的计算机理是,这个区间内的大于规定筛选重量W的数量,乘以大于筛选重量的价值,然后将总的算出来的y累加到一起,看看和规定的标准值S最小差多少,输出最小的参数W
题意:就是说给你n个矿石,然后,这n个矿石都有自己的重量w,以及其价值v,我们有一种判断机制,就是说给你m个区间范围,每次给你一个左边界L和右边界R,我们的计算机理是,这个区间内的大于规定筛选重量W的数量,乘以大于筛选重量的价值,然后将总的算出来的y累加到一起,看看和规定的标准值S最小差多少,输出最小的参数W
思路,我们发现这题数据超大,必然会有优化方法,我们通过上面·的题意可以发现,我们的参数设置的越大,能过筛选的石头越少,得到的y值越小,设置的越小,能筛选过的石头越多,得到的y值越大,因此我们可以用二分(二分的范围就是给的数据的石头的最小值到最大值,但是我们还要扩增范围,最小值减一,最大值加二)然后我们每次二分的就是参数W,然后在计算过程中要用到前缀和优化,我们要去记录出现的大于参数的矿石数目以及总价值,然后我们去计算总的Y值,Y值大于标准值S就说明,我们的参数设置的小了,要增大左边界,要是小于标准值,就说明,我们的参数设置的太大了,要缩小右边界
#include<bits/stdc++.h>
using namespace std;
#define int long long
int n,m,s;
int w[200005];
int v[200005];
int l[200005],r[200005];
int maxn=0;
int minn=0x3f3f3f3f3f3f3f3f;
int sumn[200005];
int sumv[200005];
int ans=0;//统计本次筛选的总价值
int mn=0x3f3f3f3f3f3f3f3f;//统计最小差值
bool check(int mid)
{memset(sumn,0,sizeof(sumn));memset(sumv,0,sizeof(sumv));int ans=0;//统计总的价值也就是y[i] for(int i=1;i<=n;i++){if(w[i]>=mid){sumn[i]=sumn[i-1]+1;//统计能过筛查的数量sumv[i]=sumv[i-1]+v[i];//统计能过筛查的价值 }else{sumn[i]=sumn[i-1];sumv[i]=sumv[i-1];}}for(int i=1;i<=m;i++){ans+=(sumn[r[i]]-sumn[l[i]-1])*(sumv[r[i]]-sumv[l[i]-1]);}mn=min(mn,llabs(ans-s));if(ans>s)return true;return false;
}
signed main()
{cin>>n>>m>>s;for(int i=1;i<=n;i++){cin>>w[i]>>v[i];maxn=max(maxn,w[i]);//二分的上下边界 minn=min(minn,w[i]);}int left,right,mid;for(int i=1;i<=m;i++){cin>>l[i]>>r[i];}left=minn-1,right=maxn+2;while(left<=right){mid=(left+right)/2;if(check(mid)){left=mid+1;}else{right=mid-1;}}cout<<mn;return 0;
}相关文章:

前缀和(一维前缀和+二维前缀和)
前缀和 定义: 前缀和是指某序列的前n项和,可以把它理解为数学上的数列的前n项和,而差分可以看成前缀和的逆运算。合理的使用前缀和与差分,可以将某些复杂的问题简单化。 用途: 前缀和一般用于统计一个区间的和&…...

web前端五行属性:深入探索与实战解析
web前端五行属性:深入探索与实战解析 在Web前端开发中,五行属性这一概念或许听起来有些陌生。然而,如果我们将其与前端开发的核心理念相结合,就能发现其中蕴含的深刻内涵。本文将从四个方面、五个方面、六个方面和七个方面&#…...

白酒:茅台镇白酒的酒厂社会责任与可持续发展
云仓酒庄豪迈白酒,作为茅台镇的品牌,不仅在产品品质和口感方面有着卓着的表现,在酒厂社会责任和可持续发展方面也做出了积极的探索和实践。 首先,云仓酒庄豪迈白酒注重环境保护和资源利用。酒厂在生产过程中严格控制能源消耗和排放…...

音视频开发_SDL音频播放器的实现
今天向大家介绍一下如何通过 SDL 实现一个PCM音频播放器。这是一个最简单的播放器,它不涉及到音频的解复用,解码等工作。我们只需要将音频原始数据喂给 SDL 音频接口就可以听到悦耳的声音了。在下面的列子中我将向你演示,使用 SDL 做这样一个…...
C语言学习系列:初识C语言
前言,C语言是什么 语言,比如中文、英语、法语、德语等,是人与人交流的工具。 C语言也是语言,不过是一种特殊的语言,是人与计算机交流的工具。 为什么叫C语言呢? 这就要从C语言的历史说起了。 一&#…...
利用反向代理编写HTTP抓包工具——可视化界面
手写HTTP抓包工具——可视化界面 项目描述语言golang可视化fynev2功能代理抓包、重发、记录 目录 1. 示例1.1 主界面1.2 开启反向代理1.3 抓包1.4 历史记录1.5 重发 2. 核心代码2.1 GUI2.1 抓包 3. 结语3.1 传送门 1. 示例 1.1 主界面 1.2 开启反向代理 1.3 抓包 1.4 历史记录…...

下拉框数据被遮挡 且 后续数据无法下拉的 解决方法
目录 前言1. 问题所示2. 原理分析3. 解决方法3.1 添加空白版2.2 调整z-index2.3 父容器的溢出属性2.4 调整样式属性4. 效果图前言 小程序使用的是Uniapp,原理都差不多,索性标题就不标注Uniapp(小程序) 对于该问题调试了一个晚上,最终解决,对此记录下来 1. 问题所示 执…...

课设--学生成绩管理系统(二)
欢迎来到 Papicatch的博客 目录 🐋引言 🦈编写目的 🦈项目说明 🐋产品介绍 🦈产品概要说明 🦈产品用户定位 🦈产品中的角色 🐋 产品总体业务流程图 🐋 产品功…...

STM32CubeMX配置-外部中断配置
一、简介 MCU为STM32G070,配置为上升沿触发外部中断,在上升沿外部中断回调函数中进行相关操作。 二、外部中断配置 查看规格书中管教描述,找到I/O对应的外部中断线,然后进行如下上升沿触发外部中断配置。 三、生成代码 调用上升沿…...

基于Vue的日程排班表 - common-schedule
原文:基于Vue的日程排班表 - common-schedule-CSDN博客...
SmartEDA、Multisim、Proteus大比拼:电路设计王者之争?
在电路设计领域,SmartEDA、Multisim和Proteus无疑是三款备受瞩目的软件工具。它们各自拥有独特的功能和优势,但在这场电路设计王者的竞争中,谁才是真正的领跑者?让我们深入探究这三款软件的异同,揭示它们各自的魅力所在…...

【教资科一传统文化】文化素养传统文化之神话传说、天文历法、古代称谓、中国传统节日、成语典故
目录 编辑 传统文化之天文历法 (一)四时(四季)从农历、名称上掌握 (二)二十四节气(1、名称2、季节-节气3、特殊) (三)十二时辰(1.先后顺序2.时间段3.别称) (四)五更(五夜) (五)天干地支(1.名称2.纪年) 文化素养传统文化…...
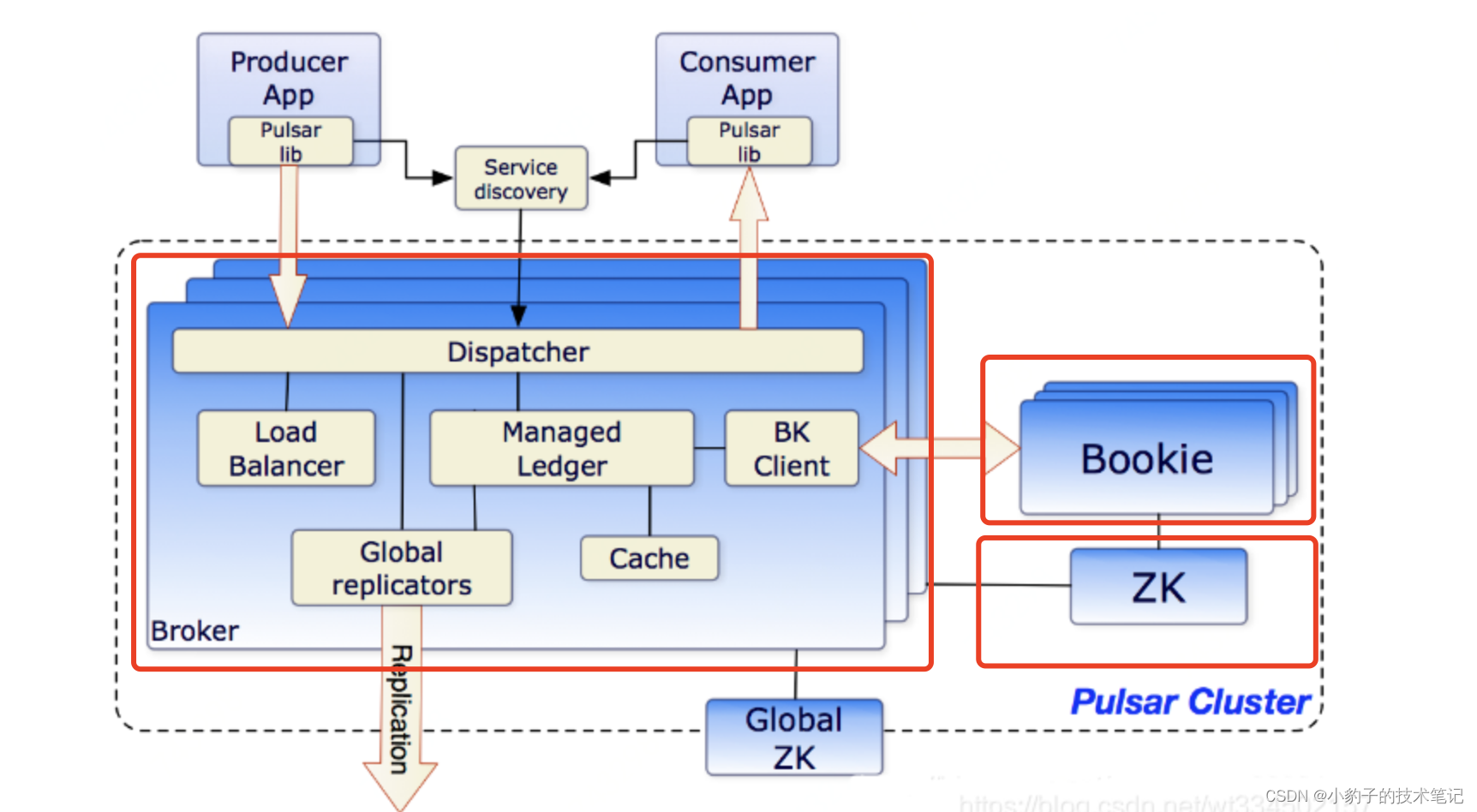
Apache Pulsar 从入门到精通
一、快速入门 Pulsar 是一个分布式发布-订阅消息平台,具有非常灵活的消息模型和直观的客户端 API。 最初由 Yahoo 开发,在 2016 年开源,并于2018年9月毕业成为 Apache 基金会的顶级项目。Pulsar 已经在 Yahoo 的生产环境使用了三年多&#…...

[Bug]使用duckduckgo的duckduckgo_search API搜索图片出现了错误
现在在kaggle上学习一个课程,第一课主要是识别图片里面是不是鸟🐦。其中一步是使用duckduckgo 搜索图片,源码: from duckduckgo_search import ddg_images from fastcore.all import * from fastbook import search_images_ddgde…...

线程池若干问题
线程池中线程异常后,销毁还是复用? 线程池在提交任务前,可以提前创建线程吗? 线程池中线程异常后,销毁还是复用? 直接说结论,需要分两种情况: 使用execute()提交任务:…...
k8s+RabbitMQ单机部署
1 k8s 配置文件yaml: apiVersion: apps/v1 kind: Deployment metadata:name: rabbitmq-deploynamespace: rz-dt spec:replicas: 1selector:matchLabels:app: rabbitmqtemplate:metadata:labels:app: rabbitmqspec:containers:- name: rabbitmqimage: "rz-dt-image-server…...

github.com/therecipe/qt windows中安装
github.com/therecipe/qt windows中安装 a.准备好源码,解压到go/src/github.com/therecipe/qtwin下 b.设置cmd环境变量: set QT_DIRM:\work\tool\Qt5.14.2\5.14.2\mingw73_64 set QT_VERSION5.14.2 set QT_API5.13.0 set QT_QMAKE_DIRM:\work\tool\Qt5.14.2\5.14.2\mingw73_64\…...

LogicFlow 学习笔记——11. 对齐线 和 键盘快捷键
对齐线 Snapline 对齐线能够在节点移动过程中,将移动节点的位置与画布中其他节点位置进行对比,辅助位置调整。位置对比有如下两个方面。 节点中心位置节点的边框 对齐线使用 普通编辑模式下,默认开启对齐线,也可通过配置进行关…...
FastWeb - Lua开源跨平台网站开发服务
在网站开发领域,大家都熟知PHPStudy和宝塔这两款广受欢迎的工具,但今天我要介绍的是一款功能强大、支持跨平台的开源Lua网站开发服务——Fast Web,以及与之配套的网站管理器。 Fast Web简介 Fast Web是一款基于Lua编写的网站开发框架&#…...

原子阿波罗STM32F767程序的控制器改为STM32F407驱动LCD屏
由于手里没有原子大神的F429开发板,又还想学习原子大神的F429开发板程序,前几天,经过更换控制器,成功把原子大神的F429开发板程序用到了F407开发板上,驱动LCD屏显示成功,目的,就是熟悉原子大神的…...

Chapter03-Authentication vulnerabilities
文章目录 1. 身份验证简介1.1 What is authentication1.2 difference between authentication and authorization1.3 身份验证机制失效的原因1.4 身份验证机制失效的影响 2. 基于登录功能的漏洞2.1 密码爆破2.2 用户名枚举2.3 有缺陷的暴力破解防护2.3.1 如果用户登录尝试失败次…...

Android Wi-Fi 连接失败日志分析
1. Android wifi 关键日志总结 (1) Wi-Fi 断开 (CTRL-EVENT-DISCONNECTED reason3) 日志相关部分: 06-05 10:48:40.987 943 943 I wpa_supplicant: wlan0: CTRL-EVENT-DISCONNECTED bssid44:9b:c1:57:a8:90 reason3 locally_generated1解析: CTR…...

深入剖析AI大模型:大模型时代的 Prompt 工程全解析
今天聊的内容,我认为是AI开发里面非常重要的内容。它在AI开发里无处不在,当你对 AI 助手说 "用李白的风格写一首关于人工智能的诗",或者让翻译模型 "将这段合同翻译成商务日语" 时,输入的这句话就是 Prompt。…...

Linux链表操作全解析
Linux C语言链表深度解析与实战技巧 一、链表基础概念与内核链表优势1.1 为什么使用链表?1.2 Linux 内核链表与用户态链表的区别 二、内核链表结构与宏解析常用宏/函数 三、内核链表的优点四、用户态链表示例五、双向循环链表在内核中的实现优势5.1 插入效率5.2 安全…...

MongoDB学习和应用(高效的非关系型数据库)
一丶 MongoDB简介 对于社交类软件的功能,我们需要对它的功能特点进行分析: 数据量会随着用户数增大而增大读多写少价值较低非好友看不到其动态信息地理位置的查询… 针对以上特点进行分析各大存储工具: mysql:关系型数据库&am…...

MODBUS TCP转CANopen 技术赋能高效协同作业
在现代工业自动化领域,MODBUS TCP和CANopen两种通讯协议因其稳定性和高效性被广泛应用于各种设备和系统中。而随着科技的不断进步,这两种通讯协议也正在被逐步融合,形成了一种新型的通讯方式——开疆智能MODBUS TCP转CANopen网关KJ-TCPC-CANP…...

如何为服务器生成TLS证书
TLS(Transport Layer Security)证书是确保网络通信安全的重要手段,它通过加密技术保护传输的数据不被窃听和篡改。在服务器上配置TLS证书,可以使用户通过HTTPS协议安全地访问您的网站。本文将详细介绍如何在服务器上生成一个TLS证…...

ElasticSearch搜索引擎之倒排索引及其底层算法
文章目录 一、搜索引擎1、什么是搜索引擎?2、搜索引擎的分类3、常用的搜索引擎4、搜索引擎的特点二、倒排索引1、简介2、为什么倒排索引不用B+树1.创建时间长,文件大。2.其次,树深,IO次数可怕。3.索引可能会失效。4.精准度差。三. 倒排索引四、算法1、Term Index的算法2、 …...

SpringCloudGateway 自定义局部过滤器
场景: 将所有请求转化为同一路径请求(方便穿网配置)在请求头内标识原来路径,然后在将请求分发给不同服务 AllToOneGatewayFilterFactory import lombok.Getter; import lombok.Setter; import lombok.extern.slf4j.Slf4j; impor…...

多种风格导航菜单 HTML 实现(附源码)
下面我将为您展示 6 种不同风格的导航菜单实现,每种都包含完整 HTML、CSS 和 JavaScript 代码。 1. 简约水平导航栏 <!DOCTYPE html> <html lang"zh-CN"> <head><meta charset"UTF-8"><meta name"viewport&qu…...
