行列视(RCV)报表中的时间是如何处理的?
答:行列视(RCV)作为一套独立、且用于数据加工、处理和展示的系统,具有一套独立的时间处理机制。报表中的指标除了数据值外,最重要的属性就是时间。主要规则介绍如下:
实时数据,时间是指当前时间;
统计报表数据,一般与报表日期有关,每个报表都有开始时间(RSD表示)、结束时间(RED表示)和绝对时间(指定时间、当年RSY、当月RSM、当日RSD、当时),其他时间都是这些时间的相对值,并且可以进行加、减计算。
如:日报中的测点“cdt158”的当日平均值取值公式:
GETV("MR","cdt158","RSD","RED","0","avg")
日报中的测点“cdt158”的昨日平均值(环比)取值公式为:
GETV("MR","cdt158","RSD-1d","RED-1d ","0","avg")
日报中的测点“cdt158”的本月截至当日平均值取值公式为:
GETV("MR","cdt158","RSM","RED ","0","avg")
日报中的测点“cdt158”的去年同期平均值取值公式为:
GETV("MR","cdt158","RSD-1y","RED-1y ","0","avg")
同理其他日期处理方式原理一致,可灵活解决报表中的时间因素,具体使用方式可参考系统使用说明书。
相关文章:
报表中的时间是如何处理的?)
行列视(RCV)报表中的时间是如何处理的?
答:行列视(RCV)作为一套独立、且用于数据加工、处理和展示的系统,具有一套独立的时间处理机制。报表中的指标除了数据值外,最重要的属性就是时间。主要规则介绍如下: 实时数据,时间是指当前时间…...

成员变量和for循环里面的变量不冲突原因
今天写项目,发现一个类中有一个成员变量与for循环块中的局部变量重名了,但是也没有报错,功能也是正常的,然后了解了一下原因: 成员变量和 for 循环块中的变量不冲突的原因在于它们的作用域(Scopeÿ…...
如何使用任意浏览器远程访问本地搭建的Jellyfin影音平台
文章目录 前言1. Jellyfin服务网站搭建1.1 Jellyfin下载和安装1.2 Jellyfin网页测试 2.本地网页发布2.1 cpolar的安装和注册2.2 Cpolar云端设置2.3 Cpolar本地设置 3.公网访问测试4. 结语 前言 本文主要分享如何使用Windows电脑本地部署Jellyfin影音服务并结合cpolar内网穿透工…...

CEM美国培安消解罐内管 CEM40位 55ML 微波消解罐
内罐采用高纯实验级进口增强改性处理TFM材料或PFA材料,我厂加工的微波罐能与原厂仪器匹配,而且是盖、体通配,无尺寸误差。精选材质,未添加回料,洁净的加工环境,优化了加工工艺,确保低本底&#…...

使用 Selenium 保持登录会话信息
使用 Selenium 保持登录会话信息 在进行 Web 自动化测试时,保持登录会话信息是一个常见的需求。这不仅能节省每次测试时重复登录的时间,还能模拟实际用户行为,使测试更加真实可靠。在这篇博客中,我们将深入探讨如何使用 Selenium 在每次启动时保持原有的登录会话信息。 什…...

程序员画图工具?那必然是你了!!【送源码】
作为一个程序员,画图是必不可少的技巧。当然此画图不是搞艺术,而是画各种架构图、流程图、泳道图以及各种示意图。 平时我不论是记笔记、写技术文章,还是工作中写文档,都需要配上各种各样的示意图。不管是帮助自己更好的掌握知识…...
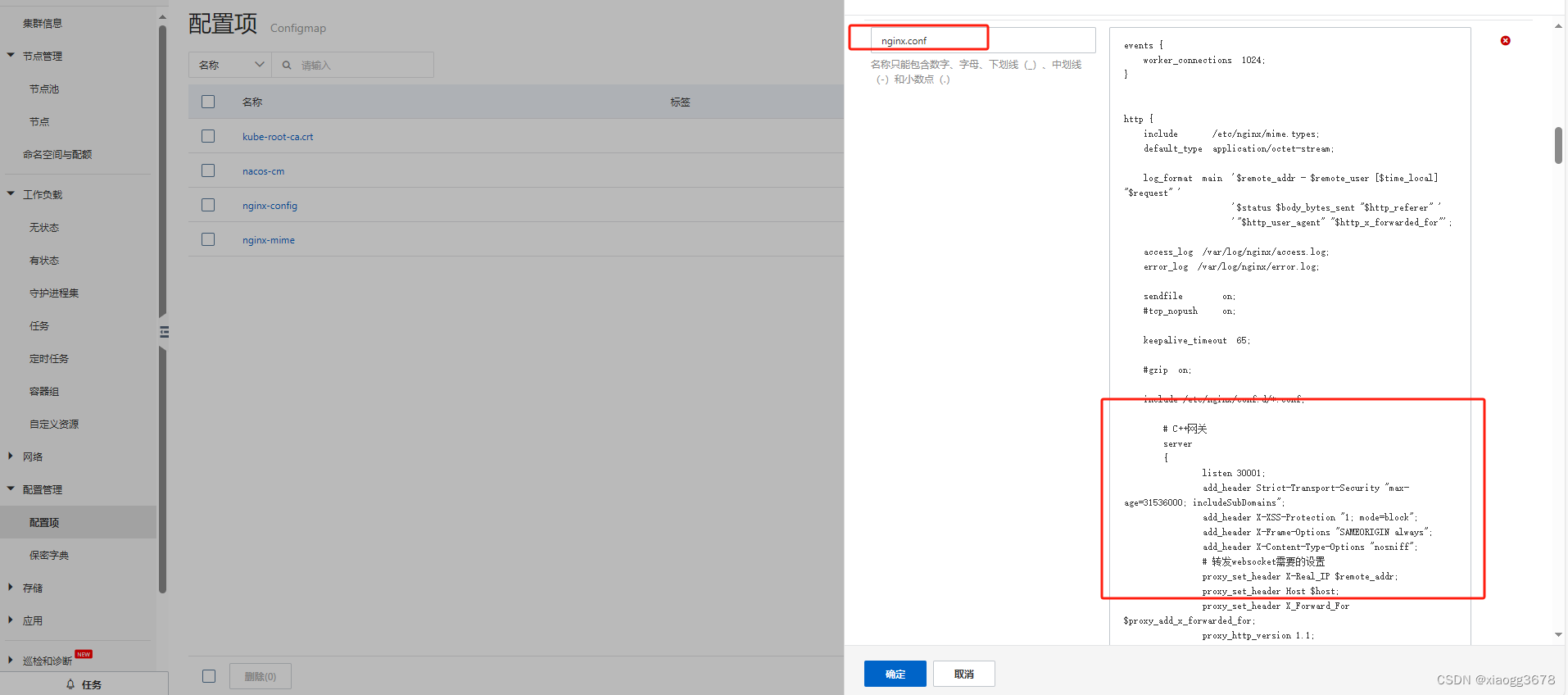
k8s nginx.conf配置文件配置
无状态nginx配置nginx.conf覆盖容器配置nginx.conf 代码:events {worker_connections 1024; }http {include /etc/nginx/mime.types;default_type application/octet-stream;log_format main $remote_addr - $remote_user [$time_local] "$request&q…...

XSKY 在金融行业:新一代分布式核心信创存储解决方案
近日,国家金融监督管理总局印发了《关于银行业保险业做好金融“五篇大文章”的指导意见》,在数字金融领域提出明确目标,要求银行业保险业数字化转型成效明显,数字化经营管理体系基本建成,数字化服务广泛普及࿰…...
第9章 类
第9章 类 9.1 创建和使用类9.1.1 创建 Dog 类9.1.2 根据类创建实例 9.2 使用类和实例9.2.1 Car 类9.2.2 给属性指定默认值9.2.3 修改属性的值 9.3 继承9.3.1 子类的方法__init__()9.3.2 给子类定义属性和方法9.3.3 重写父类的方法9.3.4 将实例用作属性9.3.5 模拟实物 9.4 导入类…...

Elasticsearch 第二期:倒排索引,分析,映射
前言 正像前面所说,ES真正强大之处在于可以从无规律的数据中找出有意义的信息——从“大数据”到“大信息”。这也是Elasticsearch一开始就将自己定位为搜索引擎,而不是数据存储的一个原因。因此用这一篇文字记录ES搜索的过程。 关于ES搜索计划分两篇或…...
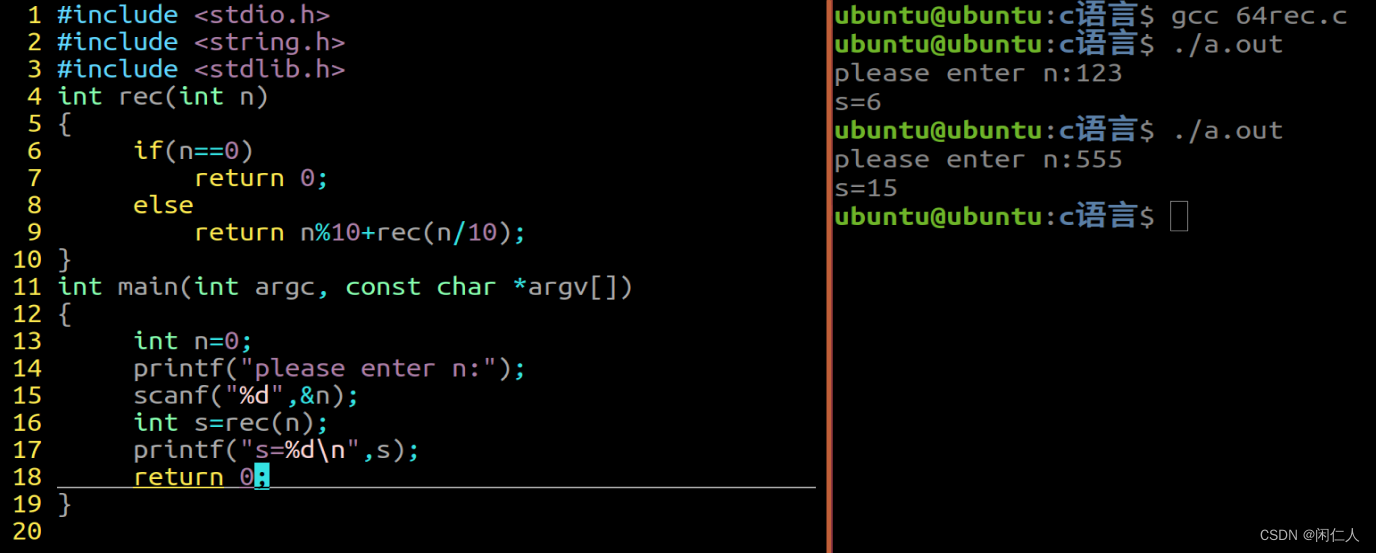
函数的一点点习题
1、利用递归计算0-n的和 #include <stdio.h> #include <string.h> #include <stdlib.h> int rec(int n) {if(n0)return 0;elsereturn nrec(n-1); } int main(int argc, const char *argv[]) {int n0;printf("please enter n:");scanf("%d&quo…...

使用Java计算Linux系统中sum命令得到的校验值
目录 ■相关知识 ・sum 命令 ・BSD校验算法是什么 ・BSD校验算法 和hash值 有区别吗 ・BSD校验算法,为什么是BSD,这个缩写代表什么 ■Java代码 ■效果 ====== ■相关知识 ・…...
】)
鸿蒙开发电话服务:【 @ohos.telephony.sms (短信服务)】
短信服务 说明: 本模块首批接口从API version 6开始支持。后续版本的新增接口,采用上角标单独标记接口的起始版本。 导入模块 import sms from ohos.telephony.sms;sms.createMessage createMessage(pdu: Array, specification: string, callback: Asy…...
算法02 递归算法及其相关问题【C++实现】
递归 在编程中,我们把函数直接或者间接调用自身的过程叫做递归。 递归处理问题的过程是:通常把一个大型的复杂问题,转变成一个与原问题类似的,规模更小的问题来进行求解。 递归的三大要素 函数的参数。在用递归解决问题时&…...

Sermant标签路由能力在同城双活场景的应用
作者:聂子雄 华为云高级软件工程师 摘要:目前应用上云已成为趋势,用户也对应用在云上的高可靠方案有更高追求,目前同城双活场景作为应用高可靠方案中的一种常见实践方案,对微服务流量提出了数据中心亲和性的要求&…...

javascript-obfuscator混淆
安装 npm install javascript-obfuscator -g 配置 重度混淆,性能低 性能下降50-100% { "compact": true, "controlFlowFlattening": true, "controlFlowFlatteningThreshold": 0.75, // 设置为0到1之间的值 "deadCodeI…...

GitHub项目里的api
在一个GitHub项目中提到的"api"通常指的是该项目提供的应用程序编程接口(Application Programming Interface)。这意味着该项目包含了一套规则和工具,允许其他开发者通过代码调用该接口来与项目功能互动、获取数据或执行特定任务。…...

k8s可练习实验分享
实验环境介绍:单master节点+3node节点 环境已提前配置完毕,如果你环境还未做,请移步 k8s集群V1.27.3安装 在 k8s 上可以做许多实验来提升你的动手能力和理解。以下是一些常见且有用的实验项目: 1、部署一个简单的应用…...

浏览器支持http-flv协议
Google Chrome 浏览器和Microsoft Edge 浏览器原生并不支持 HTTP-FLV 协议。HTTP-FLV 主要与 Flash Player 相关,而 Flash Player 已经在 2020 年底停止支持,并且 Microsoft Edge 也逐步淘汰了对 Flash 的支持。 flv.js 利用 HTML5 和 Media Source Exte…...
)
一千题,No.0077(计算谱半径)
在数学中,矩阵的“谱半径”是指其特征值的模集合的上确界。换言之,对于给定的 n 个复数空间的特征值 { a1b1i,⋯,anbni },它们的模为实部与虚部的平方和的开方,而“谱半径”就是最大模。 现在给定一些复数空间的特征值&a…...

wordpress后台更新后 前端没变化的解决方法
使用siteground主机的wordpress网站,会出现更新了网站内容和修改了php模板文件、js文件、css文件、图片文件后,网站没有变化的情况。 不熟悉siteground主机的新手,遇到这个问题,就很抓狂,明明是哪都没操作错误&#x…...

【杂谈】-递归进化:人工智能的自我改进与监管挑战
递归进化:人工智能的自我改进与监管挑战 文章目录 递归进化:人工智能的自我改进与监管挑战1、自我改进型人工智能的崛起2、人工智能如何挑战人类监管?3、确保人工智能受控的策略4、人类在人工智能发展中的角色5、平衡自主性与控制力6、总结与…...

mongodb源码分析session执行handleRequest命令find过程
mongo/transport/service_state_machine.cpp已经分析startSession创建ASIOSession过程,并且验证connection是否超过限制ASIOSession和connection是循环接受客户端命令,把数据流转换成Message,状态转变流程是:State::Created 》 St…...

【JVM】- 内存结构
引言 JVM:Java Virtual Machine 定义:Java虚拟机,Java二进制字节码的运行环境好处: 一次编写,到处运行自动内存管理,垃圾回收的功能数组下标越界检查(会抛异常,不会覆盖到其他代码…...

ServerTrust 并非唯一
NSURLAuthenticationMethodServerTrust 只是 authenticationMethod 的冰山一角 要理解 NSURLAuthenticationMethodServerTrust, 首先要明白它只是 authenticationMethod 的选项之一, 并非唯一 1 先厘清概念 点说明authenticationMethodURLAuthenticationChallenge.protectionS…...

鸿蒙DevEco Studio HarmonyOS 5跑酷小游戏实现指南
1. 项目概述 本跑酷小游戏基于鸿蒙HarmonyOS 5开发,使用DevEco Studio作为开发工具,采用Java语言实现,包含角色控制、障碍物生成和分数计算系统。 2. 项目结构 /src/main/java/com/example/runner/├── MainAbilitySlice.java // 主界…...

基于Java+VUE+MariaDB实现(Web)仿小米商城
仿小米商城 环境安装 nodejs maven JDK11 运行 mvn clean install -DskipTestscd adminmvn spring-boot:runcd ../webmvn spring-boot:runcd ../xiaomi-store-admin-vuenpm installnpm run servecd ../xiaomi-store-vuenpm installnpm run serve 注意:运行前…...

c++第七天 继承与派生2
这一篇文章主要内容是 派生类构造函数与析构函数 在派生类中重写基类成员 以及多继承 第一部分:派生类构造函数与析构函数 当创建一个派生类对象时,基类成员是如何初始化的? 1.当派生类对象创建的时候,基类成员的初始化顺序 …...

【Veristand】Veristand环境安装教程-Linux RT / Windows
首先声明,此教程是针对Simulink编译模型并导入Veristand中编写的,同时需要注意的是老用户编译可能用的是Veristand Model Framework,那个是历史版本,且NI不会再维护,新版本编译支持为VeriStand Model Generation Suppo…...

【HarmonyOS 5】鸿蒙中Stage模型与FA模型详解
一、前言 在HarmonyOS 5的应用开发模型中,featureAbility是旧版FA模型(Feature Ability)的用法,Stage模型已采用全新的应用架构,推荐使用组件化的上下文获取方式,而非依赖featureAbility。 FA大概是API7之…...
