当前位置： 首页 > news >正文

3.4.马氏链-随机游走的常返性

news 2026/2/9 5:13:24

随机游走的常返态

  • 1. 随机游走常返性定义
    • 1.1. 随机游走常返值和可能集
    • 1.2. 随机游走常返性
  • 2. 简单随机游走: 维数与常返性的关系
    • 2.1. 简单随机游走
    • 2.2. 二维及以下简单随机游走常返, 三维及以上简单随机游走非常返
  • 3. 随机游走 ( d ≤ 2 ) (d\leq 2) (d≤2): 常返的充分条件
  • 4. 随机游走( d d d 任意): 常返的充要条件
    • 4.1. 随机游走常返的等价条件-特征函数
    • 4.2. 一维随机游走常返的等价条件
    • 4.3. 二维随机游走常返的等价条件
    • 4.4. 大于三维随机游走常返的等价条件
  • 5. 应用: 调和函数的Liouville定理

1. 随机游走常返性定义

令 S n S_{n} Sn​

相关文章：

3.4.马氏链-随机游走的常返性

随机游走的常返态 1. 随机游走常返性定义1.1. 随机游走常返值和可能集1.2. 随机游走常返性2. 简单随机游走: 维数与常返性的关系2.1. 简单随机游走2.2. 二维及以下简单随机游走常返, 三维及以上简单随机游走非常返3. 随机游走 ( d ≤ 2 ) (d\leq 2) (d≤2): 常返的充分条件4. 随…...

编程日记 2024/6/18 2:10:00

HOT100与剑指Offer

文章目录 前言一、41. 缺失的第一个正数（HOT100）二、6. 从尾到头打印链表（剑指Offer）总结 前言 一个本硕双非的小菜鸡，备战24年秋招，计划刷完hot100和剑指Offer的刷题计划，加油！ 根…...

编程日记 2024/6/18 2:08:58

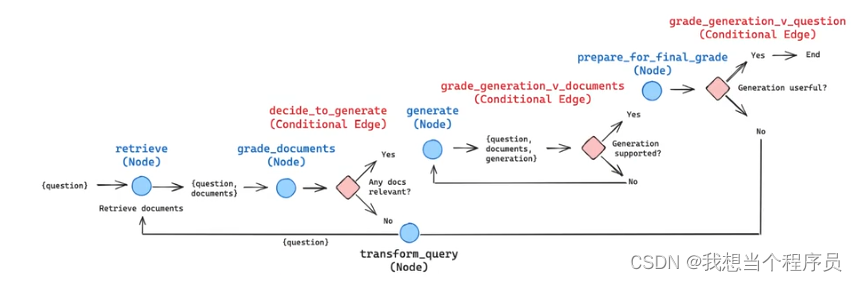
【AI开发】CRAG、Self-RAG、Adaptive-RAG

先放一张基础RAG的流程图 https://blog.langchain.dev/agentic-rag-with-langgraph/ 再放一个CRAG和self-RAG的LangChain官方博客 Corrective RAG(CRAG) 首先需要知道的是CRAG的特色发生在retrieval阶段的最后开始，即当我们获得到了近似的document（或者…...

编程日记 2024/6/18 2:06:56

FFmpeg中内存分配和释放相关的源码：av_malloc函数、av_mallocz函数、av_free函数和av_freep函数分析

一、av_malloc函数分析 （一）av_malloc函数的声明 av_malloc函数的声明放在在FFmpeg源码（本文演示用的FFmpeg源码版本为5.0.3，该ffmpeg在CentOS 7.5上通过10.2.1版本的gcc编译）的头文件libavutil/mem.h中：…...

编程日记 2024/6/18 2:04:52

七天进阶elasticsearch[Four]

依赖: <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-data-elasticsearch</artifactId>...

编程日记 2024/6/18 2:03:51

数据库-数据定义和操纵-DDL语言的使用

创建一个数据库&#xff1a; create database 数据库名; 选择数据库&#xff1a; use 数据库名; 创建表 create table 表名( ); 添加字段&#xff1b; ALTER TABLE 表名 ADD 新字段名 数据类型 [约束条件] [FIRST|AFTER 已存在字段名] ; 删除字段&#xff1a; ALTER TABLE 表…...

编程日记 2024/6/18 2:02:49

黄金价格与美元的关系变了？

在一些传统的定价框架中&#xff0c;现货黄金的价格走势取&#xff0c;决于美元的实际利率水平——实际利率越高&#xff0c;黄金价格越低&#xff0c;反之亦然。在大多数的时候&#xff0c;美元的实际利率决定了美元指数的高低所以人们通常认为&#xff0c;现货金价与美元呈反…...

编程日记 2024/6/18 2:01:48

VB.net与C# 调用InitializeComponent的区别

VB.NET与C# 调用InitializeComponent的区别 在VB.NET和C#中&#xff0c;InitializeComponent 方法的调用方式有所不同。 C#: 在C#中&#xff0c;InitializeComponent 方法通常是在构造函数中显式调用的。它用于初始化窗体和控件的属性。代码示例如下&#xff1a; public pa…...

编程日记 2024/6/18 2:00:47

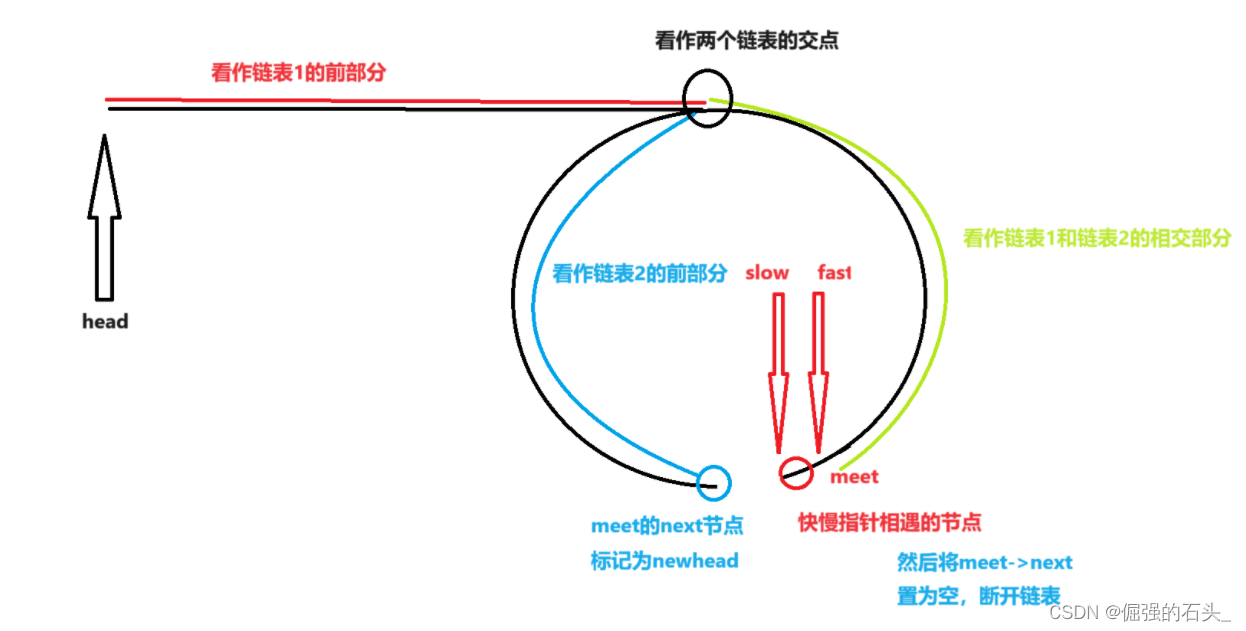
【数据结构与算法 刷题系列】求带环链表的入环节点（图文详解）

&#x1f493; 博客主页&#xff1a;倔强的石头的CSDN主页 &#x1f4dd;Gitee主页&#xff1a;倔强的石头的gitee主页 ⏩ 文章专栏&#xff1a;《数据结构与算法 经典例题》C语言 期待您的关注 ​ 目录 一、问题描述 二、解题思路 方法一&#xff1a;数学公式推导法 方法…...

编程日记 2024/6/18 1:58:43

独立游戏之路：Tap篇 -- Unity 集成 TapTap 广告详细步骤

Unity 集成 TapADN 广告详细步骤 前言一、TapTap 广告介绍二、集成 TapTap 广告的步骤2.1 进入广告后台2.2 创建广告计划2.3 选择广告类型三、代码集成3.1 下载SDK3.2 工程配置3.3 源码分享四、常见问题4.1 有展现量没有预估收益 /eCPM 波动大？4.2 新建正式媒体找不到预约游戏…...

编程日记 2024/6/18 1:55:40

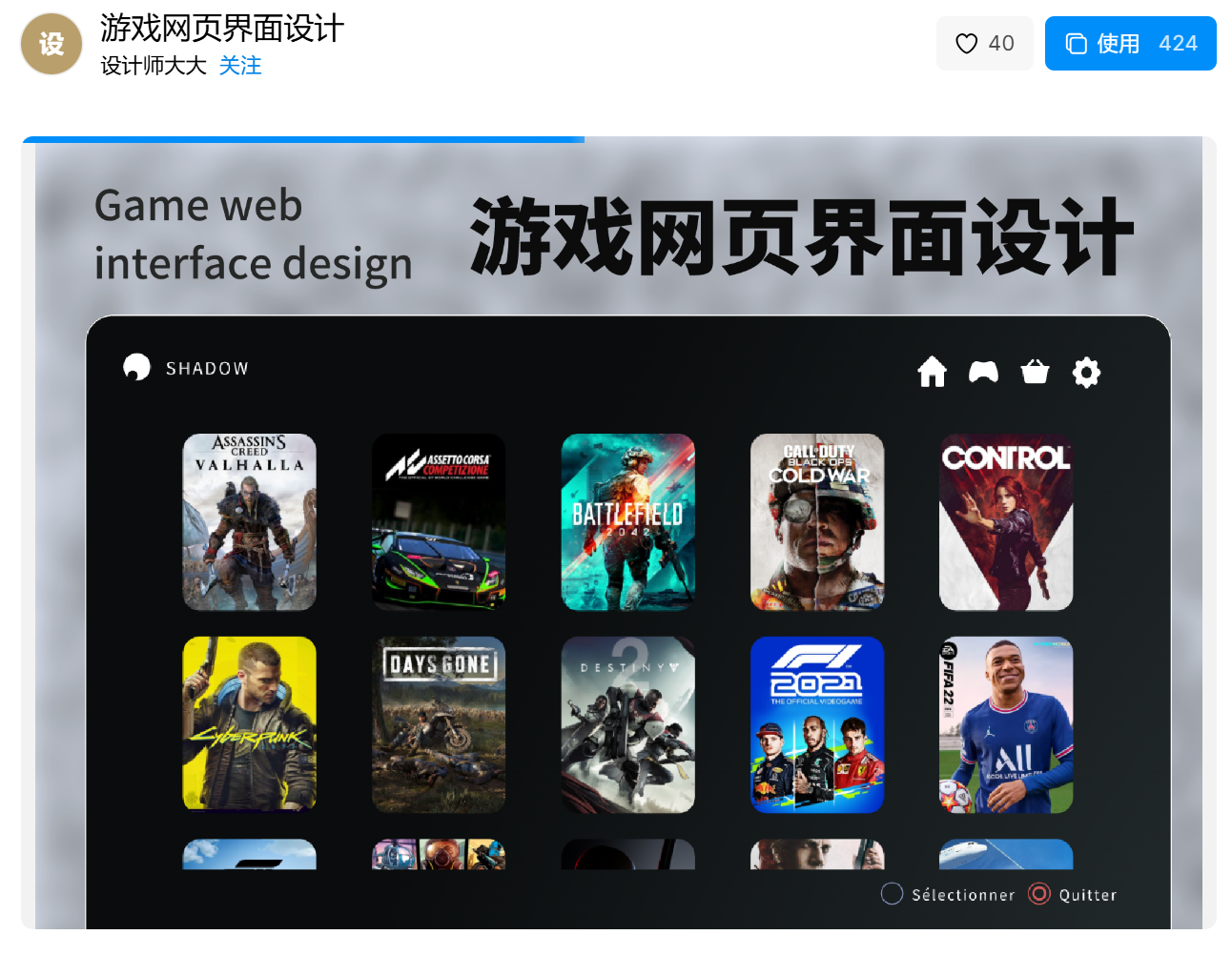
设计灵感源泉！7个令人赞叹的网页界面设计展示

网页的界面设计主要是指视觉设计和风格设计。高质量的界面更容易吸引用户的注意力&#xff0c;从而更准确地向用户传达信息。对于设计师来说&#xff0c;他们需要从高质量的作品中获得稳定的灵感&#xff0c;以帮助他们更高效地实现设计目标。在本文中&#xff0c;梳理了7个高质…...

编程日记 2024/6/18 1:54:38

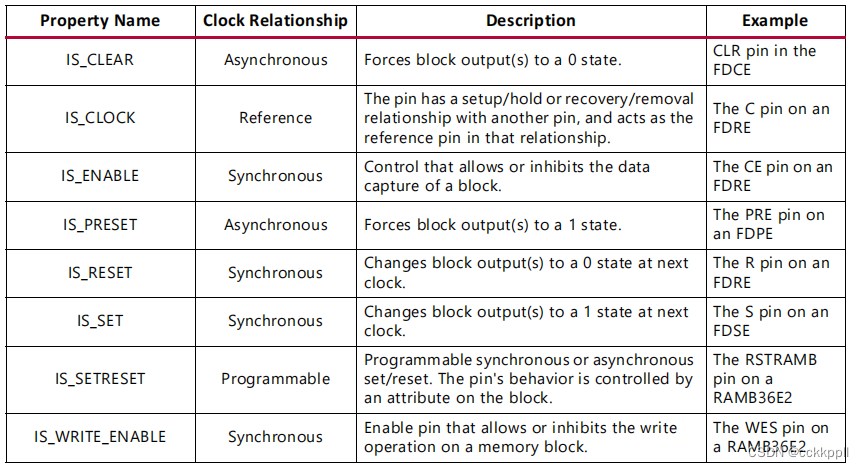
vivado PIN

描述 引脚是基元或层次单元上的逻辑连接点。引脚允许 要抽象掉单元格的内容&#xff0c;并简化逻辑以便于使用。引脚可以 是标量的&#xff0c;包含单个连接&#xff0c;或者可以定义为对多个进行分组的总线引脚 信号在一起。 相关对象 引脚连接到一个单元&#xff0c;并且可以…...

编程日记 2024/6/18 1:52:37

docker部署mysql+nginx+redis

部署mysql 1、拉去镜像 docker search mysql docker pull mysql:5.7 2、运行镜像 docker run -p 3306:3306 --name mysql \ -v /home/mysql/log:/var/log/mysql \ -v /home/mysql/data:/var/lib/mysql \ -v /home/mysql/conf:/etc/mysql/conf.d \ -v /home/mysql/mysql-files…...

编程日记 2024/6/18 1:50:35

python文件操作、文件操作、读写文件、写模式

with读取文件数据内容 with open(filepath,mode,encoding) as file:#具体操作,例如&#xff1a;print(file.read())#查看文件所有的内容。 with&#xff1a;Python中的一个上下文管理器&#xff0c;用于简化资源的管理和释放。它可以用于任意需要进行资源分配和释放的情境…...

编程日记 2024/6/18 1:48:32

【亲测可用】docker进入正在运行的容器

微信公众号&#xff1a;leetcode_algos_life&#xff0c;代码随想随记 小红书&#xff1a;412408155 CSDN&#xff1a;https://blog.csdn.net/woai8339?typeblog &#xff0c;代码随想随记 GitHub: https://github.com/riverind 抖音【暂未开始&#xff0c;计划开始】&#xf…...

编程日记 2024/6/18 1:46:30

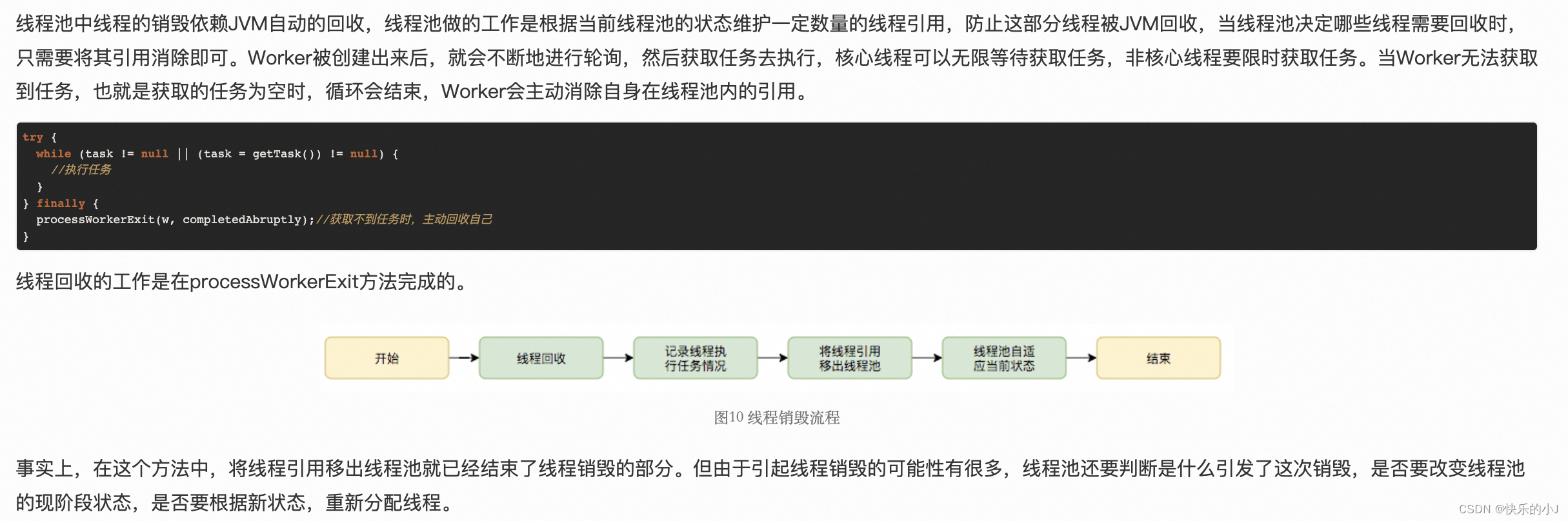
线程池吞掉异常的case：源码阅读与解决方法

1. 问题背景 有一天给同事CR&#xff0c;看到一段这样的代码 try {for (param : params) {//并发处理&#xff0c;func无返回值ThreadPool.submit(func(param));} } catch (Exception e) {log.info("func抛异常啦,参数是:{}", param) } 我&#xff1a;你这段代码是…...

编程日记 2024/6/18 1:45:29

基于mysqlbinlog恢复数据

1、把binlog转换为SQL mysqlbinlog --base64-outputdecode-rows -vv /usr/local/mysql/log-bin/mysql-bin.000003 >result.sql find / -name result.sql 2、查看events show binlog events in mysql-bin.000003; 3、回滚到3667那一行的数据 mysqlbinlog -v /usr/local/mys…...

编程日记 2024/6/18 1:43:27

Android_Android Studio 常用快捷键 for mac

功能快捷键运行ctrl R优化importctrl opt O格式化opt cmd L自动修正opt enter自动补齐cmd J自动生成代码cmd N搜索使用到的地方fn opt F7 ( cmd)搜索使用到的地方2shift cmd F搜索类cmd O当前文件搜索cmd F全局搜索按两下 shift搜索文件shift cmd O搜索符号opt…...

编程日记 2024/6/18 1:39:24

[EFI]NUC11电脑 Hackintosh 黑苹果efi引导文件

硬件型号驱动情况主板 英特尔 NUC11DBBi9&#xff08;LPC Controller WM590芯片组&#xff09; 处理器 11th Gen Intel Core i9-11900KB 3.30GHz 八核 已驱动内存32 GB ( 三星 DDR4 3200MHz 16GB x 2 )已驱动硬盘三星 MZVL21T0HCLR-00B00 (1024 GB / 固态硬盘)已驱动显卡AMD R…...

编程日记 2024/6/18 1:36:20

在Ubuntu上配置和设置防火墙UFW

在本文我们学习如何在Ubuntu上配置和设置UFW&#xff08;防火墙&#xff09;&#xff0c;UFW代表“不复杂的防火墙”&#xff0c;它充当IPTABLES的接口&#xff0c;从而简化了防火墙的配置过程&#xff0c;对于防火墙来说&#xff0c;这是非常困难的。初学者学习和配置防火墙规…...

编程日记 2024/6/18 1:34:19

label-studio的使用教程(导入本地路径)

文章目录 1. 准备环境2. 脚本启动2.1 Windows2.2 Linux 3. 安装label-studio机器学习后端3.1 pip安装(推荐)3.2 GitHub仓库安装 4. 后端配置4.1 yolo环境4.2 引入后端模型4.3 修改脚本4.4 启动后端 5. 标注工程5.1 创建工程5.2 配置图片路径5.3 配置工程类型标签5.4 配置模型5.…...

编程新知 2026/2/7 20:40:53

Maven 概述、安装、配置、仓库、私服详解

目录 1、Maven 概述 1.1 Maven 的定义 1.2 Maven 解决的问题 1.3 Maven 的核心特性与优势 2、Maven 安装 2.1 下载 Maven 2.2 安装配置 Maven 2.3 测试安装 2.4 修改 Maven 本地仓库的默认路径 3、Maven 配置 3.1 配置本地仓库 3.2 配置 JDK 3.3 IDEA 配置本地 Ma…...

编程新知 2026/2/8 1:58:01

有限自动机到正规文法转换器v1.0

1 项目简介 这是一个功能强大的有限自动机&#xff08;Finite Automaton, FA&#xff09;到正规文法&#xff08;Regular Grammar&#xff09;转换器&#xff0c;它配备了一个直观且完整的图形用户界面&#xff0c;使用户能够轻松地进行操作和观察。该程序基于编译原理中的经典…...

编程新知 2026/1/31 13:13:32

Fabric V2.5 通用溯源系统——增加图片上传与下载功能

fabric-trace项目在发布一年后，部署量已突破1000次，为支持更多场景，现新增支持图片信息上链，本文对图片上传、下载功能代码进行梳理，包含智能合约、后端、前端部分。 一、智能合约修改 为了增加图片信息上链溯源，需要对底层数据结构进行修改，在此对智能合约中的农产品数…...

编程新知 2025/9/27 12:03:43

Java + Spring Boot + Mybatis 实现批量插入

在 Java 中使用 Spring Boot 和 MyBatis 实现批量插入可以通过以下步骤完成。这里提供两种常用方法&#xff1a;使用 MyBatis 的 <foreach> 标签和批处理模式&#xff08;ExecutorType.BATCH&#xff09;。 方法一&#xff1a;使用 XML 的 <foreach> 标签&#xff…...

编程新知 2025/6/11 2:44:05

JVM虚拟机：内存结构、垃圾回收、性能优化

1、JVM虚拟机的简介 Java 虚拟机（Java Virtual Machine 简称：JVM）是运行所有 Java 程序的抽象计算机，是 Java 语言的运行环境，实现了 Java 程序的跨平台特性。JVM 屏蔽了与具体操作系统平台相关的信息，使得 Java 程序只需生成在 JVM 上运行的目标代码（字节码），就可以…...

编程新知 2026/2/7 0:37:40

Python+ZeroMQ实战：智能车辆状态监控与模拟模式自动切换

目录 关键点 技术实现1 技术实现2 摘要&#xff1a; 本文将介绍如何利用Python和ZeroMQ消息队列构建一个智能车辆状态监控系统。系统能够根据时间策略自动切换驾驶模式&#xff08;自动驾驶、人工驾驶、远程驾驶、主动安全&#xff09;&#xff0c;并通过实时消息推送更新车…...

编程新知 2025/11/12 0:06:50

论文阅读笔记——Muffin: Testing Deep Learning Libraries via Neural Architecture Fuzzing

Muffin 论文 现有方法 CRADLE 和 LEMON&#xff0c;依赖模型推理阶段输出进行差分测试&#xff0c;但在训练阶段是不可行的&#xff0c;因为训练阶段直到最后才有固定输出&#xff0c;中间过程是不断变化的。API 库覆盖低&#xff0c;因为各个 API 都是在各种具体场景下使用。…...

编程新知 2026/2/1 1:28:58

android RelativeLayout布局

<?xml version"1.0" encoding"utf-8"?> <RelativeLayout xmlns:android"http://schemas.android.com/apk/res/android"android:layout_width"match_parent"android:layout_height"match_parent"android:gravity&…...

编程新知 2026/2/6 13:49:41

通过 Ansible 在 Windows 2022 上安装 IIS Web 服务器

拓扑结构 这是一个用于通过 Ansible 部署 IIS Web 服务器的实验室拓扑。 前提条件&#xff1a; 在被管理的节点上安装WinRm 准备一张自签名的证书 开放防火墙入站tcp 5985 5986端口 准备自签名证书 PS C:\Users\azureuser> $cert New-SelfSignedCertificate -DnsName &…...

编程新知 2026/2/4 16:43:10