多元多项式的特征列与零点的关系定理
下面这个定理来自《计算机代数》6.1三角列与特征列(王东明、夏壁灿著)
【定理】
设 C = [ C 1 , … , C r ] \mathbb{C =}\left\lbrack C_{1},\ldots,C_{r} \right\rbrack C=[C1,…,Cr]为多项式组 P ⊂ K [ x ] \mathbb{P \subset}\mathcal{K\lbrack}\mathbf{x}\rbrack P⊂K[x]的特征列,且命
I i = i n i ( C i ) P i = P ∪ { I i } i = 1 , … , r I_{i} = ini\left( C_{i} \right)\ \ \ \ \ \ \mathbb{P}_{i}\mathbb{= P \cup}\left\{ I_{i} \right\}\ \ \ \ \ i = 1,\ldots,r Ii=ini(Ci) Pi=P∪{Ii} i=1,…,r
I = i n i ( C ) = { I 1 , … , I r } \mathbb{I =}ini\left( \mathbb{C} \right) = \left\{ I_{1},\ldots,I_{r} \right\} I=ini(C)={I1,…,Ir}
则
Z e r o ( C \ I ) ⊂ Z e r o ( P ) ⊂ Z e r o ( C ) Zero\left( \mathbb{C\backslash I} \right) \subset Zero\left( \mathbb{P} \right) \subset Zero\left( \mathbb{C} \right) Zero(C\I)⊂Zero(P)⊂Zero(C)
Z e r o ( P ) = Z e r o ( C \ I ) ∪ ⋃ i = 1 r Z e r o ( P i ) Zero\left( \mathbb{P} \right) = Zero\left( \mathbb{C\backslash I} \right) \cup \bigcup_{i = 1}^{r}{Zero\left( \mathbb{P}_{i} \right)} Zero(P)=Zero(C\I)∪i=1⋃rZero(Pi)
在 K \mathcal{K} K以及 K \mathcal{K} K的任意扩域中成立
【证明】
- Z e r o ( C \ I ) ⊂ Z e r o ( P ) Zero\left( \mathbb{C\backslash I} \right) \subset Zero\left( \mathbb{P} \right) Zero(C\I)⊂Zero(P)
由于 C = [ C 1 , … , C r ] \mathbb{C =}\left\lbrack C_{1},\ldots,C_{r} \right\rbrack C=[C1,…,Cr]为多项式组 P ⊂ K [ x ] \mathbb{P \subset}\mathcal{K\lbrack}\mathbf{x}\rbrack P⊂K[x]的特征列,所以 p r e m ( P , C ) = { 0 } prem\left( \mathbb{P,C} \right) = \left\{ 0 \right\} prem(P,C)={0},也就是说对于任意 P ∈ P P \in \mathbb{P} P∈P,都有
I 1 q 1 … I r q r P = ∑ i = 1 r C i I_{1}^{q_{1}}\ldots I_{r}^{q_{r}}P = \sum_{i = 1}^{r}C_{i} I1q1…IrqrP=i=1∑rCi
而对于任意的 x ∈ Z e r o ( C \ I ) x \in Zero\left( \mathbb{C\backslash I} \right) x∈Zero(C\I),都有 x ∉ Z e r o ( I 1 q 1 … I r q r ) x \notin Zero\left( I_{1}^{q_{1}}\ldots I_{r}^{q_{r}} \right) x∈/Zero(I1q1…Irqr)且 x ∈ Z e r o ( C i ) x \in Zero\left( C_{i} \right) x∈Zero(Ci),那么 P = 0 P = 0 P=0,可得 x ∈ Z e r o ( P ) x \in Zero\left( \mathbb{P} \right) x∈Zero(P),即 Z e r o ( C \ I ) ⊂ Z e r o ( P ) Zero\left( \mathbb{C\backslash I} \right) \subset Zero\left( \mathbb{P} \right) Zero(C\I)⊂Zero(P)。
- Z e r o ( P ) ⊂ Z e r o ( C ) Zero\left( \mathbb{P} \right) \subset Zero\left( \mathbb{C} \right) Zero(P)⊂Zero(C)
根据特征列的定义,有 C ⊂ ⟨ P ⟩ \mathbb{C \subset}\left\langle \mathbb{P} \right\rangle C⊂⟨P⟩,也就是
C i = ∑ P ∈ P k P P C_{i} = \sum_{P \in \mathbb{P}}^{}{k_{P}P} Ci=P∈P∑kPP
所以,当多项式 P P P的值为 0 0 0时, C i C_{i} Ci必为 0 0 0,即 Z e r o ( P ) ⊂ Z e r o ( C ) Zero\left( \mathbb{P} \right) \subset Zero\left( \mathbb{C} \right) Zero(P)⊂Zero(C)。
- Z e r o ( P ) ⊂ Z e r o ( C \ I ) ∪ ⋃ i = 1 r Z e r o ( P i ) Zero\left( \mathbb{P} \right) \subset Zero\left( \mathbb{C\backslash I} \right) \cup \bigcup_{i = 1}^{r}{Zero\left( \mathbb{P}_{i} \right)} Zero(P)⊂Zero(C\I)∪⋃i=1rZero(Pi)
设 x ∈ Z e r o ( P ) x \in Zero\left( \mathbb{P} \right) x∈Zero(P),根据2,那么有 x ∈ Z e r o ( C ) x \in Zero\left( \mathbb{C} \right) x∈Zero(C)。
若 x ∈ Z e r o ( I ) x \in Zero\left( \mathbb{I} \right) x∈Zero(I),则 x ∈ ⋃ i = 1 r Z e r o ( I i ) x \in \bigcup_{i = 1}^{r}{Zero\left( I_{i} \right)} x∈⋃i=1rZero(Ii),又因为 x ∈ Z e r o ( P ) x \in Zero\left( \mathbb{P} \right) x∈Zero(P),所以 x ∈ ⋃ i = 1 r Z e r o ( P i ) x \in \bigcup_{i = 1}^{r}{Zero\left( \mathbb{P}_{i} \right)} x∈⋃i=1rZero(Pi);
若 x ∉ Z e r o ( I ) x \notin Zero\left( \mathbb{I} \right) x∈/Zero(I),结合 x ∈ Z e r o ( C ) x \in Zero\left( \mathbb{C} \right) x∈Zero(C),可得 x ∈ Z e r o ( C \ I ) x \in Zero\left( \mathbb{C\backslash I} \right) x∈Zero(C\I)。
结合上述两种情况的讨论,可得 Z e r o ( P ) ⊂ Z e r o ( C \ I ) ∪ ⋃ i = 1 r Z e r o ( P i ) Zero\left( \mathbb{P} \right) \subset Zero\left( \mathbb{C\backslash I} \right) \cup \bigcup_{i = 1}^{r}{Zero\left( \mathbb{P}_{i} \right)} Zero(P)⊂Zero(C\I)∪⋃i=1rZero(Pi)。
- Z e r o ( P ) ⊃ Z e r o ( C \ I ) ∪ ⋃ i = 1 r Z e r o ( P i ) Zero\left( \mathbb{P} \right) \supset Zero\left( \mathbb{C\backslash I} \right) \cup \bigcup_{i = 1}^{r}{Zero\left( \mathbb{P}_{i} \right)} Zero(P)⊃Zero(C\I)∪⋃i=1rZero(Pi)
根据1, Z e r o ( C \ I ) ⊂ Z e r o ( P ) Zero\left( \mathbb{C\backslash I} \right) \subset Zero\left( \mathbb{P} \right) Zero(C\I)⊂Zero(P);
因为 Z e r o ( P i ) ⊂ Z e r o ( P ) Zero\left( \mathbb{P}_{i} \right) \subset Zero\left( \mathbb{P} \right) Zero(Pi)⊂Zero(P),所以 ⋃ i = 1 r Z e r o ( P i ) ⊂ Z e r o ( P ) \bigcup_{i = 1}^{r}{Zero\left( \mathbb{P}_{i} \right)} \subset Zero\left( \mathbb{P} \right) ⋃i=1rZero(Pi)⊂Zero(P)。
综合可得 Z e r o ( C \ I ) ∪ ⋃ i = 1 r Z e r o ( P i ) ⊂ Z e r o ( P ) Zero\left( \mathbb{C\backslash I} \right) \cup \bigcup_{i = 1}^{r}{Zero\left( \mathbb{P}_{i} \right)} \subset Zero\left( \mathbb{P} \right) Zero(C\I)∪⋃i=1rZero(Pi)⊂Zero(P)
综合1、2可得
Z e r o ( C \ I ) ⊂ Z e r o ( P ) ⊂ Z e r o ( C ) Zero\left( \mathbb{C\backslash I} \right) \subset Zero\left( \mathbb{P} \right) \subset Zero\left( \mathbb{C} \right) Zero(C\I)⊂Zero(P)⊂Zero(C)
综合3、4可得
Z e r o ( P ) = Z e r o ( C \ I ) ∪ ⋃ i = 1 r Z e r o ( P i ) Zero\left( \mathbb{P} \right) = Zero\left( \mathbb{C\backslash I} \right) \cup \bigcup_{i = 1}^{r}{Zero\left( \mathbb{P}_{i} \right)} Zero(P)=Zero(C\I)∪i=1⋃rZero(Pi)
相关文章:

多元多项式的特征列与零点的关系定理
下面这个定理来自《计算机代数》6.1三角列与特征列(王东明、夏壁灿著) 【定理】 设 C [ C 1 , … , C r ] \mathbb{C }\left\lbrack C_{1},\ldots,C_{r} \right\rbrack C[C1,…,Cr]为多项式组 P ⊂ K [ x ] \mathbb{P \subset}\mathcal{K\lbrack}\…...

git - LFS 使用方法
安装Git LFS 访问 Git LFS官网 下载适用于您操作系统的版本。 Linux用户,解压缩下载的.tar.gz文件,并通过终端运行安装脚本。 tar -xvf git-lfs-linux-amd64-vX.Y.Z.tar.gz cd git-lfs-X.Y.Z sudo ./install.sh 初始化Git LFS # 全局启用 git lfs i…...

提高磁盘可靠性的技术:保障数据安全的四大方法
目录 1. 第一级容错技术 磁盘镜像(Mirroring) 工作原理 RAID 1 工作原理 优点 缺点 适用场景 示例 2. 第二级容错技术 概述 RAID 5 RAID 6 优点 缺点 适用场景 3. 基于集群系统的容错技术 概述 Hadoop HDFS Ceph 优点 缺点 适用场…...
CesiumJS【Basic】- #006 浏览器控制台查看位置角度
文章目录 浏览器控制台查看位置角度1 目标 浏览器控制台查看位置角度 1 目标 浏览器控制台查看位置角度...

Mac 终端报错 zsh: command not found: brew 解决方案
Homebrew安装 /bin/bash -c "$(curl -fsSL https://raw.githubusercontent.com/Homebrew/install/HEAD/install.sh)"安装成功后,在终端输入下面命令 brew -v如果成功输出brew版本,则安装成功 关闭终端重新打开终端,报错zsh: comm…...

详解 HBase 的常用 API
一、环境准备 创建一个 Maven 工程并引入依赖 <dependency><groupId>org.apache.hbase</groupId><artifactId>hbase-server</artifactId><version>1.3.1</version> </dependency> <dependency><groupId>org.apach…...
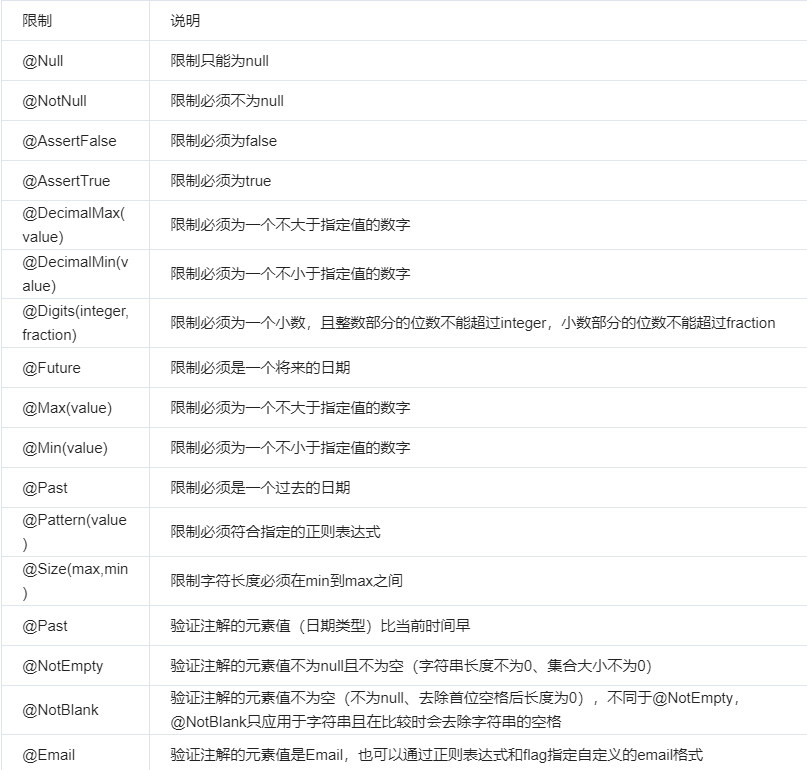
JSR303校验
校验的需求 前端请求后端接口传输参数,需要校验参数。 在controller中需要校验参数的合法性,包括:必填项校验、数据格式校验等在service中需要校验业务规则,比如:课程已经审核过了,所以提交失败。 servi…...

04 远程访问及控制
1、SSH远程管理 SSH是一种安全通道协议,主要用来实现字符界面的远程登录、远程复制等功能。 SSH协议对通信双方的数据传输进行了加密处理(包括用户登陆时输入得用户口令)。 终端:接收用户的指令 TTY终端不能远程,它…...

[晕事]今天做了件晕事38 shell里的source 点号
今天碰到一个问题脚本里使用点号引入某个文件形式如下: . /tmp/abc但是脚本运行出现错误,一开始还以为是/tmp没有可执行权限(https://mzhan017.blog.csdn.net/article/details/112178736#t16),导致abc运行不了。 后来…...

java如何分割字符串
java要实现对字符串的分割,需要用到split语句 语法格式是 str.split(分隔符) 其中 str是字符串 示例代码如下 public class Stringsplit {public static void main(String[] args) {String a"蒸羊羔,蒸熊掌,蒸鹿尾,烧花…...
胡说八道(24.6.12)——数字电子技术以及Modelsim
上回书说到数电中的最常用的表达式——逻辑表达式(由布尔代数组成)以及常用的两种图表——真值表(真值表表示的是所有的输入可能的线性组合以及输出)和卡诺图(卡诺图则是一种化简工具,排除冗余项,合并可合并项)。 今天,先来看看昨天说的基本逻…...

【Android面试八股文】AsyncTask中的任务是串行的还是并行的
文章目录 串行执行并行执行示例代码串行执行(默认)并行执行总结AsyncTask 的任务执行方式可以是串行的,也可以是并行的,这取决于使用的执行器 ( Executor)。 串行执行 默认情况下,AsyncTask 使用的是 SERIAL_EXECUTOR,即任务按顺序一个接一个地执行。这意味着下一个任务…...
无人机RTMP推流EasyDSS直播平台推流成功,不显示直播按钮是什么原因?
互联网视频云平台/视频点播直播/视频推拉流EasyDSS支持HTTP、HLS、RTMP等播出协议,并且兼容多终端,如Windows、Android、iOS、Mac等。为了便于用户集成与二次开发,我们也提供了API接口供用户调用和集成。在无人机场景上,可以通过E…...

经验分享,xps格式转成pdf格式
XPS 是一种电子文档格式、后台打印文件格式和页面描述语言。有时候微软默认打印机保存的是xps格式,我们如何转换为pdf格式呢,这里分享一个免费好用的网站,可以实现。 网站:https://xpstopdf.com/zh/ 截图:...
基于51单片机的音乐彩灯设计
基于51单片机的音乐彩灯设计 (程序+原理图+设计报告) 功能介绍 具体功能: 由STC单片机ADC0809模块LM386功放模块喇叭音频接口发光二极管电源构成 1.通过音频线输入可以播放电脑、手机、MP3里面的音乐。 2.AD对音频…...

API接口设计的艺术:如何提升用户体验和系统性能
在数字时代,API接口的设计对于用户体验和系统性能有着至关重要的影响。良好的设计可以显著提升应用程序的响应速度、可靠性和易用性。以下是几个关键点,帮助改善API接口的设计: 1. 理解并定义清晰的要求 用户研究:与最终用户进行…...

韩兴国/姜勇团队在《Trends in Plant Science》发表植物根系氮素再分配的观点文章!
氮素是陆地生态系统中的关键限制性营养元素,通过生物固氮和土壤氮供应通常远低高等植物的氮需求。当土壤氮素供应无法充分满足植物茎叶生长需求时,植物会通过自身营养器官(如根或根茎)再分配来实现氮的内部循环和再利用。尽管植物…...
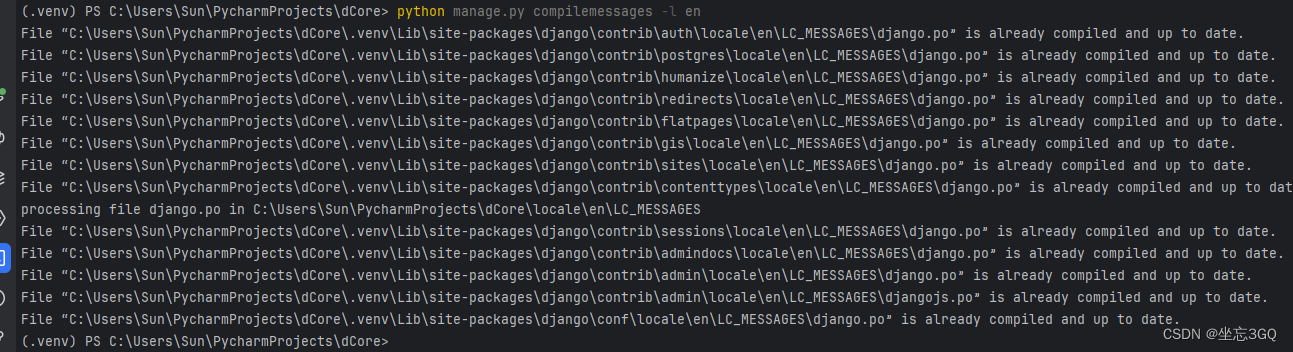
52.Python-web框架-Django - 多语言编译-fuzzy错误
目录 1.起因 2.原因 3.解决方法 3.1手动移除fuzzy标记 3.2重新生成po文件,并检查是否还存在fuzzy标记 3.3重新编译生成mo文件 1.起因 在Django的国际化和本地化过程中,当你发现某些字段仅显示msgid,而不显示msgstr时,可能是…...

Linux自旋锁
面对没有获取锁的现场,通常有两种处理方式。 互斥锁:堵塞自己,等待重新调度请求自旋锁:循环等待该锁是否已经释放 本文主要讲述自旋锁 自旋锁其实是一种很乐观的锁,他认为只要再等一下下锁便能释放,避免…...
服务器----阿里云服务器重启或关机,远程连接进不去,个人博客无法打开
问题描述 在使用阿里云免费的新加坡服务器时,发现重启或者是关机在开服务器后,就会出现远程连接不上、个人博客访问不了等问题 解决方法 进入救援模式连接主机,用户名是root,密码是自己设置的 点击访问博客查看更多内容...

日语AI面试高效通关秘籍:专业解读与青柚面试智能助攻
在如今就业市场竞争日益激烈的背景下,越来越多的求职者将目光投向了日本及中日双语岗位。但是,一场日语面试往往让许多人感到步履维艰。你是否也曾因为面试官抛出的“刁钻问题”而心生畏惧?面对生疏的日语交流环境,即便提前恶补了…...

sqlserver 根据指定字符 解析拼接字符串
DECLARE LotNo NVARCHAR(50)A,B,C DECLARE xml XML ( SELECT <x> REPLACE(LotNo, ,, </x><x>) </x> ) DECLARE ErrorCode NVARCHAR(50) -- 提取 XML 中的值 SELECT value x.value(., VARCHAR(MAX))…...

Unit 1 深度强化学习简介
Deep RL Course ——Unit 1 Introduction 从理论和实践层面深入学习深度强化学习。学会使用知名的深度强化学习库,例如 Stable Baselines3、RL Baselines3 Zoo、Sample Factory 和 CleanRL。在独特的环境中训练智能体,比如 SnowballFight、Huggy the Do…...

SAP学习笔记 - 开发26 - 前端Fiori开发 OData V2 和 V4 的差异 (Deepseek整理)
上一章用到了V2 的概念,其实 Fiori当中还有 V4,咱们这一章来总结一下 V2 和 V4。 SAP学习笔记 - 开发25 - 前端Fiori开发 Remote OData Service(使用远端Odata服务),代理中间件(ui5-middleware-simpleproxy)-CSDN博客…...

DBLP数据库是什么?
DBLP(Digital Bibliography & Library Project)Computer Science Bibliography是全球著名的计算机科学出版物的开放书目数据库。DBLP所收录的期刊和会议论文质量较高,数据库文献更新速度很快,很好地反映了国际计算机科学学术研…...

DeepSeek源码深度解析 × 华为仓颉语言编程精粹——从MoE架构到全场景开发生态
前言 在人工智能技术飞速发展的今天,深度学习与大模型技术已成为推动行业变革的核心驱动力,而高效、灵活的开发工具与编程语言则为技术创新提供了重要支撑。本书以两大前沿技术领域为核心,系统性地呈现了两部深度技术著作的精华:…...

第八部分:阶段项目 6:构建 React 前端应用
现在,是时候将你学到的 React 基础知识付诸实践,构建一个简单的前端应用来模拟与后端 API 的交互了。在这个阶段,你可以先使用模拟数据,或者如果你的后端 API(阶段项目 5)已经搭建好,可以直接连…...

RLHF vs RLVR:对齐学习中的两种强化方式详解
在语言模型对齐(alignment)中,强化学习(RL)是一种重要的策略。而其中两种典型形式——RLHF(Reinforcement Learning with Human Feedback) 与 RLVR(Reinforcement Learning with Ver…...

分布式光纤声振传感技术原理与瑞利散射机制解析
分布式光纤传感技术(Distributed Fiber Optic Sensing,简称DFOS)作为近年来迅速发展的新型感知手段,已广泛应用于边界安防、油气管道监测、结构健康诊断、地震探测等领域。其子类技术——分布式光纤声振传感(Distribut…...
MySQL 数据库深度剖析:事务、SQL 优化、索引与 Buffer Pool
在当今数据驱动的时代,数据库作为数据存储与管理的核心,其性能与可靠性至关重要。MySQL 作为一款广泛使用的开源数据库,在众多应用场景中发挥着关键作用。在这篇博客中,我将围绕 MySQL 数据库的核心知识展开,涵盖事务及…...
