离散数学复习
1.关系的介绍和性质
(1)序偶和笛卡尔积
两个元素按照一定的顺序组成的二元组就是序偶,使用尖括号进行表示,尖括号里面的元素一般都是有顺序的;
笛卡尔积就是有两个集合,从第一个集合里面选择一个元素,第二个集合选择一个元素,这个集合之间的笛卡尔积就是这两个集合元素的随机组合,因此这个笛卡尔积就类似于这个向量之间的叉乘,不满足这个交换律和结合律;
如果想让两个集合的笛卡尔积的结果是空的,当且仅当这两个集合都是空的才会出现这个情况;
概括来讲,这个序偶表示的就是一个二元组,笛卡尔积的结果里面的每一个元素都是序偶,笛卡尔积反映的也是两个集合之间的一种关系;
(2)二元关系
首先指出:关系就是笛卡尔积的子集(高度概括)!!!!!!!
二元关系就是两个元素之间的关系,这个和前面的笛卡尔积是有联系的,因为这个假设有12两个集合,第一个集合里面有12345这五个元素,第二个集合里面有678910这五个元素,他们这两个集合之间相互匹配,就会形成多种关系,如果某个集合在这个关系里面,我们就说这个是这个集合上面的关系;
通过下面的这个例子我们也可以明白两个集合进行这个笛卡尔积的运算,一共就有4个序偶,但是却可以产生16种关系;实际上,这个分为了一元子集,二元子集,三元子集,四元子集等等,就是这上面的4个序偶之间不断地相互匹配就组成了这16种关系;


(3)特殊的关系
需要留意的就是下面的这三种:
空关系:这个关系里面没有任何的序偶;
全关系:这个关系就是两个集合的笛卡尔积;
恒等关系:组成这个集合的序偶的两个元素是一样的;

(4)布尔矩阵的交并运算
这个和我们的矩阵运算是不一样的,因为这个要求这两个布尔矩阵的行数列数是完全一样的,而且是这两个矩阵的指定位置上面的元素进行运算,交就是进行对应位置元素的合取运算,并就是进行对应位置元素的析取运算;
(5)布尔矩阵的积运算
这个就是和我们的线性代数里面的矩阵运算是一样的,但是这个时候全部都是01之间的运算,而且这个结果矩阵的元素要想是1,要求这个两个对应位置进行运算的元素都是1才可以;
(6)关系的运算
关系里面涉及到复合运算,就是两个关系之间使用小圆圈进行连接的运算,这个时候只需要注意的就是从后向前进行这个传递就可以了;这个满足结合律,
关系的逆运算就是让这个序偶里面的两个元素的位置颠倒即可;
关系的幂运算就是自己向自己进行这个关系的合成;
(7)关系的性质
&&自反性,反自反性
首先要知道这个性质是对于这个关系而言的,我们首先要知道建立在这个集合上面的关系,然后再进行判断这个关系是否符合这些性质;
自反性就是对于这个集合里面的每一个元素,这个关系里面都有自己和自己的序偶,就是这个序偶的两个元素是一样的;
反自反就是不存在自己和自己的关联,都是不同的元素之间的关系;
在矩阵上面就会体现出来这个自反性的矩阵就是对角线上面的元素都是1,反自反性就是对角线上面的元素都是0,两个都不是的话就是主对角线上面的元素有的是0,有的是1;

&&对称性,反对称性
对称性就是如果有<x,y>这个序偶,那么就需要有<y,x>这个序偶;
反对称性就是不能同时存在<x,y>和<y,x>,可以这样进行判断;
下面的这个例子,第一个就是对称的,13,31同时存在,第二个就是反对称的,13存在反过来就没有存在,注意的就是这个xx这种两个元素相同的序偶是对于我们判断这个对称性和反对称性是没有影响的,因此我们判断某个关系是不是满足对称性和反对称性的时候不需要关注这个两个元素相同的序偶;
第三个的话,就是因为这个12存在,但是21不存在,因此这个就不满足对称性的条件,13存在,但是31也同样存在,这个就不满足反对称性的条件;
第四个就是纯一色的恒等关系你,对于我们判断这个对称性,反对称性没有影响,因此两个关系都是满足的;

&&传递性
这个是很容易理解的,<xy>存在,<y,z>存在,那么这个<x,z>就一定存在,这个关系就是传递性的关系;
同理,在进行这个传递性的判断的时候,这个相同的元素组成的序偶也不会影响我们对于这个传递性的判断,我们可以直接忽略;
这个第二个例子为什么是传递的,这个需要使用这个定义和蕴含式的真假判断,通过判断这个只有一个序偶的关系,这个传递性定义的前件是不成立的,因此这个肯定是符合传递性的;

(8)等价关系
等价关系的定义就是同时满足这个自反关系,对称关系,传递关系的关系,这三个需要同时满足,缺一不可;
以4为模的同余关系就是一个等价的关系,这个需要我们自己进行这个列举出来,就是x-4可以被4整除,列举之后可以字面进行判断,也可以画出来这个有向图进行判断;

等价类就是具有相同关系的数据的集合,这个里面的048的等价类是一样的,都是{0,4,8}这个集合
1 5 9这三个元素的等价类也是一样的,都是{11,5,9}这个集合,我们自己可以画出有向图出来,这个159之间具有这个相同的关系,同理048之间也是具有相同的关系的,我们把这些具有相同关系的数据称之为等价类;
通过下面的这个数据我们可以观察到,这个任何数的等价类都是非空的,有的元素的等价类是一样的,有的元素的等价类是不一样的;

相关文章:

离散数学复习
1.关系的介绍和性质 (1)序偶和笛卡尔积 两个元素按照一定的顺序组成的二元组就是序偶,使用尖括号进行表示,尖括号里面的元素一般都是有顺序的; 笛卡尔积就是有两个集合,从第一个集合里面选择一个元素&am…...

华为网络设备高频命令
1.system-view • 用法:在用户视图下执行 system-view 命令。 • 作用:进入系统视图,以便进行配置性的操作。 • 场景:当需要对设备进行系统级的配置时。 2.sysname XXX • 用法:执行 [Huawei]sysname XXX 命令。…...

信友队:南风的收集
C. [202406C]楠枫的收集 文件操作 时间限制: 1000ms 空间限制: 262144KB 输入文件名: 202406C.in 输出文件名: 202406C.out Accepted 100 分 题目描述 一年四季,寒暑交替,楠枫总是会收集每一个季节的树叶,并把它们制作成标本收集起来。当…...
)
找工作小项目:day16-重构核心库、使用智能指针(3)
day16-重构核心库、使用智能指针(3) 最后将使用这个库的方式进行展示。 1、客户端 在while ((o getopt(argc, argv, optstring)) ! -1)所有的操作都是获取参数的操作,threads 、msgs 和wait 分别指线程数、消息长度以及等待时间。 创建一…...
软考中级|软件设计师-知识点整理
目录 计算机网络概论 计算机系统基础知识 中央处理单元 数据表示 校验码 计算机体系结构 计算机体系结构的发展 存储系统 输入/输出技术 安全性、可靠性与系统性能评测基础知识 加密技术和认证技术 计算机可靠性 程序设计语言基础知识 程序设计语言概述 程序设计…...

HTML5基础
1 HTML基础概念(难点) WWW(World Wide Web,万维网)是一种建立在 Internet 上的信息资源网络。 WWW 有 3 个基本组成部分,分别是 URL:Universal Resource Locators,统一资源定位器 HT…...

python,ipython 和 jupyter notebook 之间的关系
python,ipython 和 jupyter notebook 之间的关系 文章目录 python,ipython 和 jupyter notebook 之间的关系1. Python2. IPython3. Jupyter Notebook启动 Jupyter Notebook 关系总结 Python、IPython 和 Jupyter Notebook 是相互关联但具有不同功能的工具…...
聊聊DoIP吧(三)-端口号port
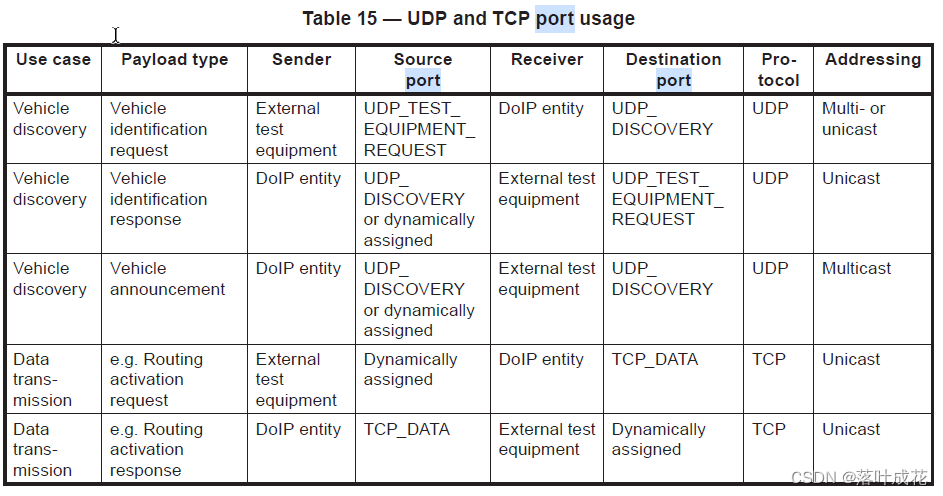
DoIP在UDP和TCP建立连接和发送诊断报文的过程中使用的端口定义如下:...
【将xml文件转yolov5训练数据txt标签文件】连classes.txt都可以生成
将xml文件转yolov5训练数据txt标签文件 前言一、代码解析 二、使用方法总结 前言 找遍全网,我觉得写得最详细的就是这个博文⇨将xml文件转yolov5训练数据txt标签文件 虽然我还是没有跑成功。那个正则表达式我不会改QWQ,但是不妨碍我会训练ai。 最终成功…...

针对k8s集群已经加入集群的服务器进行驱逐
例如k8s 已经有很多服务器,现在由于服务器资源过剩,需要剥离一些服务器出来 查找节点名称: kubectl get nodes设置为不可调度: kubectl cordon k8s-node13恢复可调度 kubectl uncordon k8s-node13在驱逐之前先把需要剥离驱逐的节…...
go 1.22 增强 http.ServerMux 路由能力
之前 server func main() {http.HandleFunc("/", func(w http.ResponseWriter, r *http.Request) {fmt.Println("Received request:", r.URL.Path)fmt.Fprintf(w, "Hello, client! You requested: %s\n", r.URL.Path)})log.Println("Serv…...
)
赶紧收藏!2024 年最常见 20道设计模式面试题(二)
上一篇地址:赶紧收藏!2024 年最常见 20道设计模式面试题(一)-CSDN博客 三、解释抽象工厂模式,并给出一个实际应用的例子。 抽象工厂模式是一种创建型设计模式,用于创建一系列相关或依赖对象的接口&#x…...

Java面向对象设计 - Java泛型约束
Java面向对象设计 - Java泛型约束 无限通配符 通配符类型由问号表示,如<?> 。 对于通用类型,通配符类型是对象类型用于原始类型。 我们可以将任何已知类型的泛型分配为通配符类型。 这里是示例代码: // MyBag of String type M…...

什么是内存泄漏?如何避免内存泄漏?
**内存泄漏(Memory Leak)**是指在程序运行过程中,已经动态分配的堆内存由于某种原因程序未释放或无法释放,造成系统内存的浪费,导致程序运行速度减慢甚至系统崩溃等严重后果。内存泄漏具有隐蔽性、积累性的特征&#x…...
(Python))
元组(tuple)(Python)
文章目录 一、定义二、常用操作 一、定义 tuple ("张三", "李四", "王二")二、常用操作 分类关键字/函数/方法说明查询元组[索引]根据索引取值,索引不存在会报错len(元组)元组长度(元素个数)值 in 元组&…...

【C++进阶学习】第二弹——继承(下)——挖掘继承深处的奥秘
继承(上):【C进阶学习】第一弹——继承(上)——探索代码复用的乐趣-CSDN博客 前言: 在前面我们已经讲了继承的基础知识,让大家了解了一下继承是什么,但那些都不是重点,今…...
LangChain-ChatGLM本地搭建|报错合集(win10)
安装过程 1. 创建虚拟环境 conda create -n langchain-chatglm python3.10 conda activate langchain-chatglm2. 部署 langchain-ChatGLM git clone https://github.com/imClumsyPanda/langchain-ChatGLMpip3 install -r requirements.txt pip3 install -U gradio pip3 inst…...

IP地址简介
一、IP地址 Internet Protocol Address,即网络层协议地址,是IP的缩写。 二、IP地址的作用 为什么不直接使用MAC,又加了一个IP地址呢? 事实上底层传输,最终使用的肯定是MAC地址,但是由于在以前&#x…...

谈吐的艺术
被人表扬,该怎么回应 你越是说自己其实没那么好, 对方出于客气, 就越是要证明你其实比你说的好得多。 O可能遇到的问题 每当工作和学习上做出点成绩,有人夸奖我的时候,我都会觉得很尴尬。因为不谦虚会得罪人ÿ…...

Linux 和 分区
文章目录 流程挂载设备文件名 Linux 下各分区的含义家目录 流程 在windows中,一个硬盘要使用只需要分区、格式化之后就可以使用了 在linux中,除了分区和格式化之外,还需要一个叫挂载的操作 挂载 挂载,就相当于windows环境下的写…...

【大模型RAG】拍照搜题技术架构速览:三层管道、两级检索、兜底大模型
摘要 拍照搜题系统采用“三层管道(多模态 OCR → 语义检索 → 答案渲染)、两级检索(倒排 BM25 向量 HNSW)并以大语言模型兜底”的整体框架: 多模态 OCR 层 将题目图片经过超分、去噪、倾斜校正后,分别用…...

[2025CVPR]DeepVideo-R1:基于难度感知回归GRPO的视频强化微调框架详解
突破视频大语言模型推理瓶颈,在多个视频基准上实现SOTA性能 一、核心问题与创新亮点 1.1 GRPO在视频任务中的两大挑战 安全措施依赖问题 GRPO使用min和clip函数限制策略更新幅度,导致: 梯度抑制:当新旧策略差异过大时梯度消失收敛困难:策略无法充分优化# 传统GRPO的梯…...
: K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?)
云原生核心技术 (7/12): K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?
大家好,欢迎来到《云原生核心技术》系列的第七篇! 在上一篇,我们成功地使用 Minikube 或 kind 在自己的电脑上搭建起了一个迷你但功能完备的 Kubernetes 集群。现在,我们就像一个拥有了一块崭新数字土地的农场主,是时…...

Spark 之 入门讲解详细版(1)
1、简介 1.1 Spark简介 Spark是加州大学伯克利分校AMP实验室(Algorithms, Machines, and People Lab)开发通用内存并行计算框架。Spark在2013年6月进入Apache成为孵化项目,8个月后成为Apache顶级项目,速度之快足见过人之处&…...
)
React Native 导航系统实战(React Navigation)
导航系统实战(React Navigation) React Navigation 是 React Native 应用中最常用的导航库之一,它提供了多种导航模式,如堆栈导航(Stack Navigator)、标签导航(Tab Navigator)和抽屉…...

MongoDB学习和应用(高效的非关系型数据库)
一丶 MongoDB简介 对于社交类软件的功能,我们需要对它的功能特点进行分析: 数据量会随着用户数增大而增大读多写少价值较低非好友看不到其动态信息地理位置的查询… 针对以上特点进行分析各大存储工具: mysql:关系型数据库&am…...

条件运算符
C中的三目运算符(也称条件运算符,英文:ternary operator)是一种简洁的条件选择语句,语法如下: 条件表达式 ? 表达式1 : 表达式2• 如果“条件表达式”为true,则整个表达式的结果为“表达式1”…...

dedecms 织梦自定义表单留言增加ajax验证码功能
增加ajax功能模块,用户不点击提交按钮,只要输入框失去焦点,就会提前提示验证码是否正确。 一,模板上增加验证码 <input name"vdcode"id"vdcode" placeholder"请输入验证码" type"text&quo…...

大语言模型如何处理长文本?常用文本分割技术详解
为什么需要文本分割? 引言:为什么需要文本分割?一、基础文本分割方法1. 按段落分割(Paragraph Splitting)2. 按句子分割(Sentence Splitting)二、高级文本分割策略3. 重叠分割(Sliding Window)4. 递归分割(Recursive Splitting)三、生产级工具推荐5. 使用LangChain的…...

【论文笔记】若干矿井粉尘检测算法概述
总的来说,传统机器学习、传统机器学习与深度学习的结合、LSTM等算法所需要的数据集来源于矿井传感器测量的粉尘浓度,通过建立回归模型来预测未来矿井的粉尘浓度。传统机器学习算法性能易受数据中极端值的影响。YOLO等计算机视觉算法所需要的数据集来源于…...
