【动态规划】0-1背包问题
【动态规划】0-1背包问题
题目:现在有四个物品,背包总容量为8,背包最多能装入价值为多少的物品?

我的图解

表格a【i】【j】表示的是容量为j的背包装入前i个物品的最大价值。
拿a【1】【1】来说,它的值就是背包容量为1,只考虑编号0,1的物品时,背包所能装入的最大价值;
然后既然是动态规划,那就一定有初值,也就是a【0】【j】 = 0; a【i】【0】 = 0;即第一行和第一列都为0;
然后根据初值来推后面的值;
首先要判断本行所对应的物品是否能装入背包,
拿a【1】【1】来说,首先要判断,若只考虑编号为1的物品,它是否可以装入背包,此时的背包容量为1,而编号为1的物品的体积为2,故它无法装入背包,那么a【1】【1】的值和背包容量为1,只考虑编号为0的物品时,背包所能装入的最大价值(即a【0】【1】)是相等的;
若能装入背包;那么有两种选择:
(1)装入本行物品,即先装入本行的物品,然后剩下背包容量装其他价值之和最大的物品
(2)不装本行物品,即背包容量都用来装除了本行物品之外的其他物品(即本行前面几行的物品)
然后比较(1)(2)选择较大者;
拿a【2】【4】来说,此时的背包容量为4,编号为2的物品的体积为3,故2号物品能装入背包,然后两种选择:
(1)装入2号物品,此时背包剩余容量为1,此时只剩下两个物品,那就是编号为0和1的物品,查表得a【1】【1】=0
故此时的最大价值为a【1】【1】加上2号物品的价值,也就是4
(2)不装2号物品,即背包容量都用来装除了本行物品之外的其他物品(即本行前面几行的物品)
由于不装入2号物品,此时的最大价值和只考虑编号为0,1物品,背包容量为4的情况的最大价值(即a【1】【4】)是相等的,
也就是3;
故选择(1)(2)中较大者,a【2】【4】=4;
依次类推下去。
解法归纳:
一、如果装不下当前物品,那么前n个物品的最佳组合和前n-1个物品的最佳组是一
样的。
二、如果装得下当前物品。
假设1:装当前物品,在给当前物品预留了相应空间的情况下,前n-1 个物品的最佳组
合加上当前物品的价值就是总价值。
假设2:不装当前物品,那么前n个物品的最佳组合和前n-1个物品的最佳组合是一样
的。
选取假设1和假设2中较大的价值,为当前最佳组合的价值。
代码实现
package eunm.Try;//0-1背包问题
public class BB {public static void main(String[] args) {// TODO 自动生成的方法存根int volume[] = {2, 3, 4, 5};int value[] = {3, 4, 5, 6};int maxvolume = 9;System.out.println(knapsack(volume, value, maxvolume));}public static int knapsack(int[] volume, int[] value, int maxvolume) {int n = volume.length;//最大价值数组为maxvalue[N+1][maxvolume+1],因为我们要从0开始保存int[][] maxvalue = new int[n + 1][maxvolume + 1];//体积和物品为0时,价值为0for (int j = 0; j < maxvolume + 1; j++) {maxvalue[0][j] = 0;}for (int i = 0; i < n + 1; i++) {maxvalue[i][0] = 0;}//i:只拿前i件物品(这里的i因为取了0,所以对应到weight和value里面都是i-1号位置)//j:假设能取的总体积为j//n是物品件数for (int i = 1; i <= n; i++) {for (int j = 1; j <= maxvolume; j++) {//当前最大价值等于放上一件的最大价值maxvalue[i][j] = maxvalue[i - 1][j];//如果当前件的体积小于总体积,可以放进去或者拿出别的东西再放进去if (volume[i - 1] <= j) {/*比较(不放这个物品的价值)和(这个物品的价值value[i - 1] 加上 当前能放的总体积减去当前物品体积j - volume[i - 1]时取前i-1个物品时的对应体积时候的最高价值)maxvalue[i - 1][j - volume[i - 1]]的大小*/if (value[i - 1] + maxvalue[i - 1][j - volume[i - 1]] > maxvalue[i - 1][j]) {maxvalue[i][j] = value[i - 1] + maxvalue[i - 1][j - volume[i - 1]];}}}}return maxvalue[n][maxvolume];}}
这里比较关键。
//如果当前件的体积小于总体积,可以放进去或者拿出别的东西再放进去if (volume[i - 1] <= j) {/*比较(不放这个物品的价值)和(这个物品的价值value[i - 1] 加上 当前能放的总体积减去当前物品体积j - volume[i - 1]时取前i-1个物品时的对应体积时候的最高价值)maxvalue[i - 1][j - volume[i - 1]]的大小*/if (value[i - 1] + maxvalue[i - 1][j - volume[i - 1]] > maxvalue[i - 1][j]) {maxvalue[i][j] = value[i - 1] + maxvalue[i - 1][j - volume[i - 1]];}}
背包问题回溯:在使得背包内总价值最大的情况下,背包内装了哪些物品?

这里我暂时不想研究了呜呜脑阔疼。
再来一个今天做的题目:小明是一个大胖子,为了让体重达到正常水平,他的计划是:减掉n千克体重,分多周完成(至少是2周),每周都减重正整数千克。为了激励自己,他决定每周减掉的体重都必须比上周减掉的体重多。假设他上周减重0千克,他从这周开始执行计划,请问可以设计出多少种方案?
套一下上面的模板就行。
package Excepect;import java.util.Scanner;public class AAAA {public static void main(String[] args) {Scanner scan = new Scanner(System.in);int n = scan.nextInt();long[][] dp = new long[n][n + 1];dp[0][0] = 1;for (int i = 1; i < n; i++) {//i表示接收体重后体重变化dp[i][0] = 1;//第一周开始减最少从1开始for (int j = 1; j <= n; j++) {//j表示能减的总体重//当前方案=上一体重的方案dp[i][j] = dp[i - 1][j];//如果当前体重<=能减的总体重if (i <= j) {//最多总方案=现有方案+(能减的总体重-当前体重时取前i-1对应体重的最多总方案)dp[i][j] = dp[i][j] + dp[i - 1][j - i];}}}System.out.println(dp[n - 1][n]);scan.close();}
}
突然发现学算法真的很费脑子。。。。。。最近两天家里面在干活,我不仅时刻被叫去帮忙干活还要去帮忙做午饭,没办法农村家庭里的孩子就是这么命苦呜呜呜,所以就没办法专注下来学习,断断续续的。
不过总结确实是一件好事,不总结的话我可能都学不懂什么。前天晚上弄的那个个人博客吧,就如同我朋友说的一样,我像极了瞎猫碰见死耗子,到处乱碰,看看碰到了没。。。
然后一直搞到深夜十二点半才在我的博客主页看到了我写的文章。目前还没成功,还没把博客部署到服务器上,好像就是差这一步来着。等我搞好了我会写一篇技术文的嘿嘿嘿。
本文由mdnice多平台发布
相关文章:

【动态规划】0-1背包问题
【动态规划】0-1背包问题 题目:现在有四个物品,背包总容量为8,背包最多能装入价值为多少的物品? 我的图解 表格a【i】【j】表示的是容量为j的背包装入前i个物品的最大价值。 拿a【1】【1】来说,它的值就是背包容量为1,只考虑…...

WordPress 高级缓存插件 W3 Total Cache Pro 详细配置教程
说起来有关 WordPress 缓存插件明月已经发表过不少文章了,但有关 W3 Total Cache Pro 这个 WordPress 高级缓存插件除了早期【网站缓存插件 W3 Total Cache,适合自己的才是最好的!】一文后就很少再提及了,最近因为明月另一个网站【玉满斋】因为某些性能上的需要准备更换缓存…...
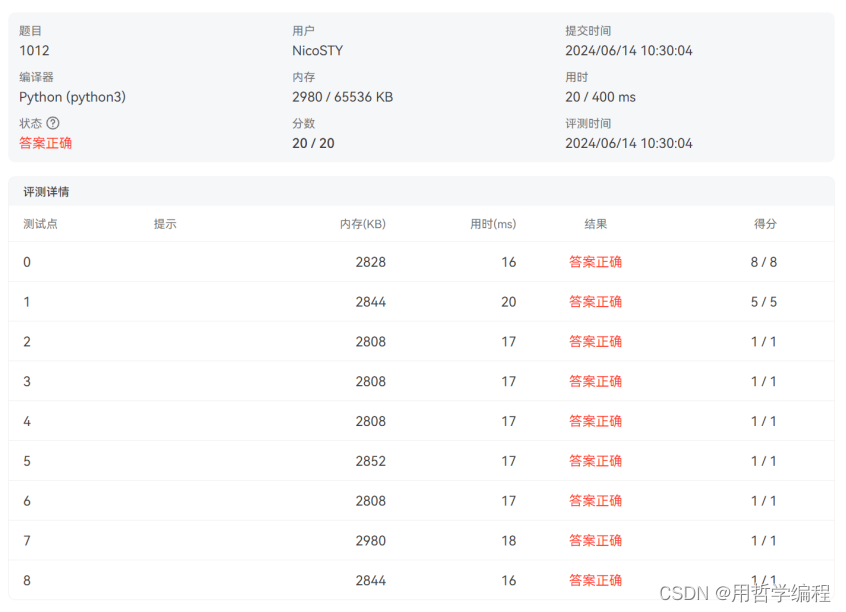
每日一题——Python实现PAT乙级1012 数字分类(举一反三+思想解读+逐步优化)五千字好文
一个认为一切根源都是“自己不够强”的INTJ 个人主页:用哲学编程-CSDN博客专栏:每日一题——举一反三Python编程学习Python内置函数 Python-3.12.0文档解读 目录 我的写法 代码优点 代码缺点 时间复杂度 空间复杂度 代码改进建议 我要更强 哲…...

Unity2D游戏制作入门 | 13 ( 之人物三段攻击 )
上期链接:Unity2D游戏制作入门 | 12(之人物受伤和死亡的逻辑动画)-CSDN博客 上期我们聊了人物的受伤和死亡的逻辑和动画,我们主要学习了事件的执行,即我们在人物受伤时可能会触发很多的事件,比如触发人物受伤的动画以及播放音乐等…...

DAY04 HTMLCSS
文章目录 一 表单(1) 数字控件(2) 颜色控件(3) 日期控件(4) 月份控件(5) 星期控件(6) 搜索控件(7) 范围控件 二 浮动框架三 结构化标签四 CSS1 CSS概述2 CSS的编写位置1. inline style 行内样式2. inner style 内部样式3. outer style 外部样式4. 小结 3 CSS选择器1. 通用选择器…...

Linux_理解程序地址空间和页表
目录 1、进程地址空间示意图 2、验证进程地址空间的结构 3、验证进程地址空间是虚拟地址 4、页表-虚拟地址与物理地址 5、什么是进程地址空间 6、进程地址空间和页表的存在意义 6.1 原因一(效率性) 6.2 原因二(安全性) …...
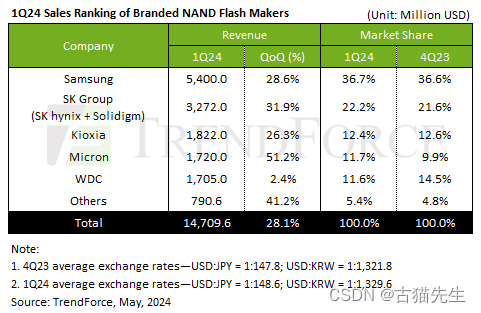
NAND闪存市场彻底复苏
在全球内存市场逐渐走出阴霾、迎来复苏曙光之际,日本存储巨头铠侠(Kioxia)凭借敏锐的市场洞察力和及时的战略调整,成功实现了从生产紧缩到全面复苏的华丽转身。这一转变不仅彰显了企业在逆境中的生存智慧,也为全球半导…...
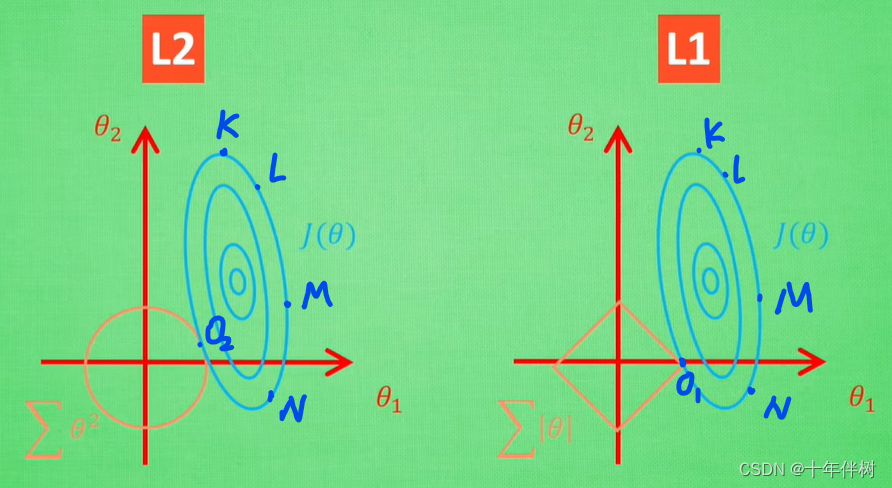
过拟合与正则化
Location Beijing 过拟合 对于一个模型 A A A,解向量空间为 θ \theta θ,误差函数用式1表示 J ( θ ) J a c c [ y θ ( x ) − y ] 2 (1) J(\theta)J_{acc}[y_\theta(x)-y]^2\tag{1} J(θ)Jacc[yθ(x)−y]2(1) 首先我们考虑用模型 A A A拟合下…...

VMware挂载NAS存储异常处理
问题概述 由于非法关机或恢复,NFS存储可能会出现以下问题: 数据存储处于挂起状态或无法正常识别。虚拟机的配置文件或虚拟磁盘仍然注册在异常数据存储上。系统误认为有虚拟机在使用该数据存储。 问题对策 下面是详细的排查步骤和解决对策:…...

Redis 7.x 系列【4】命令手册
有道无术,术尚可求,有术无道,止于术。 本系列Redis 版本 7.2.5 源码地址:https://gitee.com/pearl-organization/study-redis-demo 文章目录 1. 说明2. 命令手册2.1 Generic2.2 数据类型2.2.1 String2.2.2 Hash2.2.3 List2.2.4 S…...

走进Elasticsearch
什么是ES 是一个分布式、RESTful风格的搜索和数据分析引擎 中文参考文档: 《Elasticsearch中文文档》 | Elasticsearch 技术论坛 elasticSearch官网: Functions and Operators | Elasticsearch Guide [7.11] | Elastic查询方式 Kibana查询(原…...

QT TCP服务器和客户端示例程序
下面是一个简单的 Qt TCP 服务器和客户端示例,演示了如何使用 vSetDriver、vSetListener 和 vTcpServerStart 函数。假设 vSetDriver 和 vSetListener 是你定义的自定义函数。 TCP 服务器部分 tcpserver.h #ifndef TCPSERVER_H #define TCPSERVER_H#include <QT…...
Xlua三方库Android编译出错解决办法
Xlua三方库Android编译出错解决办法 最近听老师的热更教程,讲到xlua编译android平台会报错,也是看了老师的博客,按照方法去解决,然而问题并没有解决。应该是因为代码更新或者版本不一样,在此简单记录一下解决过程。 参…...

美国犹他州立大学《Nature Geoscience》(IF=18)!揭示草本植物对土壤有机碳的重要贡献!
随着全球变暖的影响越来越显著,碳固定成为了一个备受关注的话题。在这个背景下,热带草原被认为是一个潜在的碳固定区域。然而,目前的研究主要关注于在热带草原中种植树木,以期望增加土壤有机碳含量。但是,热带草原中的…...

高考专业抉择计算机专业热度不减,兴趣、实力与挑战并存。
作为一名即将步入大学校门的高考生,我对于计算机相关专业是否仍是热门选择感到困惑。在过去几年里,计算机科学与技术、人工智能、网络安全、软件工程等专业一直备受追捧,吸引了无数学生。然而,随着市场竞争加剧和市场饱和度提高&a…...

Flask-RQ
Flask-RQ库教程 Flask-RQ 是一个用于在 Flask 应用中集成 RQ(Redis Queue)的扩展。RQ 是一个简单的 Python 库,用于将任务排入 Redis 队列并异步执行这些任务。这对于处理长时间运行的任务(如发送电子邮件、生成报告等࿰…...

LeetCode 58. 最后一个单词的长度
LeetCode 58. 最后一个单词的长度 你一个字符串 s,由若干单词组成,单词前后用一些空格字符隔开。返回字符串中 最后一个 单词的长度。 单词 是指仅由字母组成、不包含任何空格字符的最大子字符串 示例 1: 输入:s “Hello World”…...
3阶段提交协议(3pc)
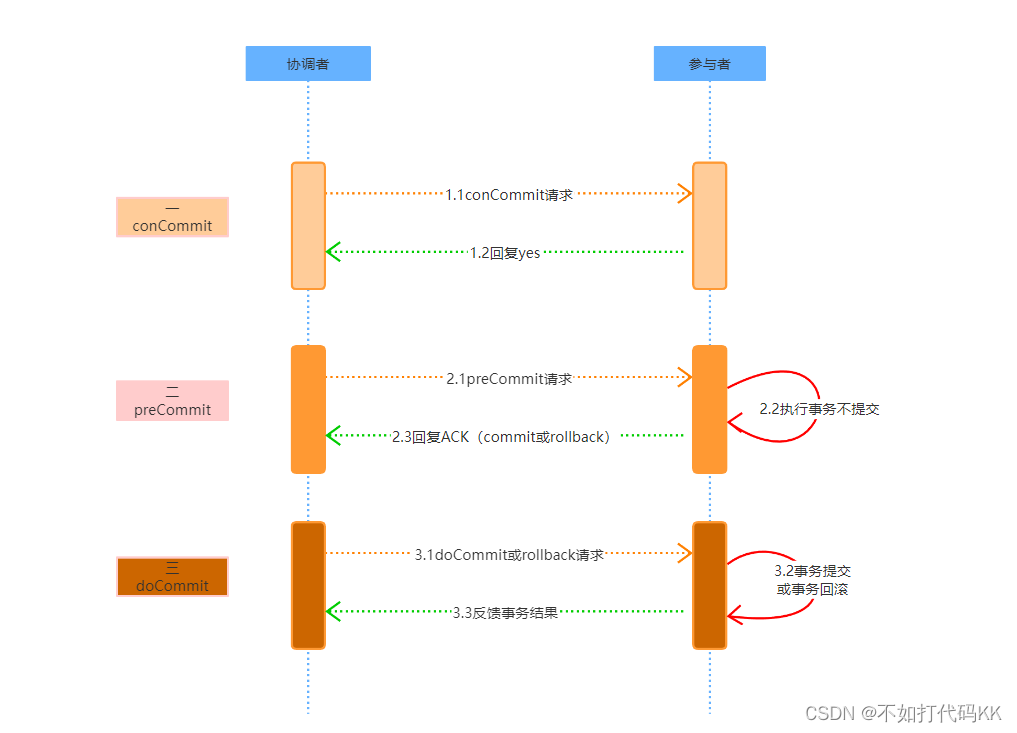
3阶段提交协议(3pc) 1 简介 三阶段提交协议是一个强一致、中心化的原子提交协议。解决了分布式事务、副本容错等分布式问题。其核心思想是将2PC的二阶段提交协议的“准备阶段”一分为二,形成了由CanCommit、PreCommit、DoCommit三个阶段组成…...

802.11中的各种帧
在无线网络中,802.11协议定义了三种类型的帧:管理帧(Management Frames)、控制帧(Control Frames)和数据帧(Data Frames)。每种类型的帧都有其特定的功能,帮助维护和管理…...

SAP PP学习笔记21 - 计划策略的Customize:策略组 > 策略 > 需求类型 > 需求类(消费区分,计划区分)
上面几章讲了MTS,MTO,ATO的计划策略。 本章来讲一下它的后台 Customize。 1,Customizeing:Planned Indep.Reqmts Management 这是配置计划策略的整个过程: - Requirements Type / Class 需求类型 / 需求类 - Plann…...

突破不可导策略的训练难题:零阶优化与强化学习的深度嵌合
强化学习(Reinforcement Learning, RL)是工业领域智能控制的重要方法。它的基本原理是将最优控制问题建模为马尔可夫决策过程,然后使用强化学习的Actor-Critic机制(中文译作“知行互动”机制),逐步迭代求解…...

如何在看板中体现优先级变化
在看板中有效体现优先级变化的关键措施包括:采用颜色或标签标识优先级、设置任务排序规则、使用独立的优先级列或泳道、结合自动化规则同步优先级变化、建立定期的优先级审查流程。其中,设置任务排序规则尤其重要,因为它让看板视觉上直观地体…...

libfmt: 现代C++的格式化工具库介绍与酷炫功能
libfmt: 现代C的格式化工具库介绍与酷炫功能 libfmt 是一个开源的C格式化库,提供了高效、安全的文本格式化功能,是C20中引入的std::format的基础实现。它比传统的printf和iostream更安全、更灵活、性能更好。 基本介绍 主要特点 类型安全:…...

全面解析数据库:从基础概念到前沿应用
在数字化时代,数据已成为企业和社会发展的核心资产,而数据库作为存储、管理和处理数据的关键工具,在各个领域发挥着举足轻重的作用。从电商平台的商品信息管理,到社交网络的用户数据存储,再到金融行业的交易记录处理&a…...

热烈祝贺埃文科技正式加入可信数据空间发展联盟
2025年4月29日,在福州举办的第八届数字中国建设峰会“可信数据空间分论坛”上,可信数据空间发展联盟正式宣告成立。国家数据局党组书记、局长刘烈宏出席并致辞,强调该联盟是推进全国一体化数据市场建设的关键抓手。 郑州埃文科技有限公司&am…...

【Redis】Redis从入门到实战:全面指南
Redis从入门到实战:全面指南 一、Redis简介 Redis(Remote Dictionary Server)是一个开源的、基于内存的键值存储系统,它可以用作数据库、缓存和消息代理。由Salvatore Sanfilippo于2009年开发,因其高性能、丰富的数据结构和广泛的语言支持而广受欢迎。 Redis核心特点:…...

使用homeassistant 插件将tasmota 接入到米家
我写一个一个 将本地tasmoat的的设备同通过ha集成到小爱同学的功能,利用了巴法接入小爱的功能,将本地mqtt转发给巴法以实现小爱控制的功能,前提条件。1需要tasmota 设备, 2.在本地搭建了mqtt服务可, 3.搭建了ha 4.在h…...

多模态大语言模型arxiv论文略读(112)
Assessing Modality Bias in Video Question Answering Benchmarks with Multimodal Large Language Models ➡️ 论文标题:Assessing Modality Bias in Video Question Answering Benchmarks with Multimodal Large Language Models ➡️ 论文作者:Jea…...

OCC笔记:TDF_Label中有多个相同类型属性
注:OCCT版本:7.9.1 TDF_Label中有多个相同类型的属性的方案 OCAF imposes the restriction that only one attribute type may be allocated to one label. It is necessary to take into account the design of the application data tree. For exampl…...

如何在Spring Boot中使用注解动态切换实现
还在用冗长的if-else或switch语句管理多个服务实现? 相信不少Spring Boot开发者都遇到过这样的场景:需要根据不同条件动态选择不同的服务实现。 如果告诉你可以完全摆脱条件判断,让Spring自动选择合适的实现——只需要一个注解,你是否感兴趣? 本文将详细介绍这种优雅的…...
