代码随想录第四十一天打卡
01背包问题 二维
代码随想录
视频讲解:带你学透0-1背包问题!| 关于背包问题,你不清楚的地方,这里都讲了!| 动态规划经典问题 | 数据结构与算法_哔哩哔哩_bilibili
#include <iostream>
#include <vector>
using namespace std;
int n,bag;
void solve(){vector<int>weight(n,0);vector<int>value(n,0);for (int i=0;i<n;i++)cin>>weight[i];for (int i=0;i<n;i++)cin>>value[i];vector<vector<int>>dp(n,vector<int>(bag+1,0));for (int i=weight[0];i<=bag;i++)dp[0][i]=value[0];for (int i=1;i<n;i++){//物品for (int j=0;j<=bag;j++){//背包容量if (j<weight[i])dp[i][j]=dp[i-1][j];else dp[i][j]=max(dp[i-1][j],dp[i-1][j-weight[i]]+value[i]);}}cout<<dp[n-1][bag];
}
int main(){cin>>n>>bag;solve();return 0;
}01背包问题 一维
代码随想录
视频讲解:带你学透01背包问题(滚动数组篇) | 从此对背包问题不再迷茫!_哔哩哔哩_bilibili
#include <iostream>
#include <vector>
using namespace std;
int n, bag;
void solve() {vector<int>weight(n, 0);vector<int>value(n, 0);for (int i = 0; i < n; i++)cin >> weight[i];for (int i = 0; i < n; i++)cin >> value[i];vector<int>dp(bag + 1, 0);for (int i = 0; i < n; i++) {for (int j =bag ; j >=weight[i] ;j--) {dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);}}cout << dp[bag] << endl;
}
int main() {cin >> n >> bag;solve();}416. 分割等和子集
本题是 01背包的应用类题目
代码随想录
视频讲解:动态规划之背包问题,这个包能装满吗?| LeetCode:416.分割等和子集_哔哩哔哩_bilibili
class Solution {
public:bool canPartition(vector<int>& nums) {int sum=0;for (int num:nums)sum+=num;if (sum%2==1)return false;else sum/=2;vector<int>dp(sum+1,0);for (int i=0;i<nums.size();i++){//物品for (int j=sum;j>=nums[i];j--){//背包容量dp[j]=max(dp[j],dp[j-nums[i]]+nums[i]);}}if (dp.back()!=sum)return false;else return true;}
};
相关文章:

代码随想录第四十一天打卡
01背包问题 二维 代码随想录 视频讲解:带你学透0-1背包问题!| 关于背包问题,你不清楚的地方,这里都讲了!| 动态规划经典问题 | 数据结构与算法_哔哩哔哩_bilibili #include <iostream> #include <vector>…...

矩阵补全IGMC 学习笔记
目录 Inductive Graph-based Matrix Completion (IGMC) 模型 igmc推理示例: Inductive Graph-based Matrix Completion (IGMC) 模型 原版代码: IGMC/models.py at master muhanzhang/IGMC GitHub GNN推理示例 torch_geometric版本:tor…...

面试题之CSS
1. 引入样式的方式 外部样式 link import 区别 内部样式 /* 写在头部标签 */ <style></style>行内样式 2. 三行代码画三角形 .triangle{width:0px;border:100px solid;border-color:transparent transparent transparent red; }3.属性的继承 可继承的属性 …...
MFC扩展库BCGControlBar Pro v35.0新版亮点:重新设计的工具栏编辑器等
BCGControlBar库拥有500多个经过全面设计、测试和充分记录的MFC扩展类。 我们的组件可以轻松地集成到您的应用程序中,并为您节省数百个开发和调试时间。 BCGControlBar专业版 v35.0已全新发布了,这个版本改进类Visual Studio 2022的视觉主题、增强对多个…...

python调用SDK的问题
问题:Could not find module MvCameraControl.dll 原因:识别环境变量runtime异常 解决:指定具体绝对地址即可。MvCameraControl.dll的位置C:\Program Files (x86)\Common Files\MVS\Runtime\Win64_x64 MvCamCtrldll WinDLL("MvCamer…...
html入门综合练习
综合练习 通过实际项目练习可以更好地理解和掌握HTML、CSS和JavaScript。以下是几个综合练习项目的建议: 项目1:个人简历网页 创建一个包含以下内容的个人简历网页: 个人简介(姓名、照片、联系方式)教育背景工作经…...

函数模板的具体化
函数模板优点是通用性,可以解决某个方面的普遍性问题,但是这个世界上的事情不是绝对的,有普遍的,就有绝对的。举个栗子: #include <iostream> using namespace std; template <typename T> void Swap(T &…...

【Linux 内存管理】
文章目录 1. 为什么要有虚拟内存呢?🔍 1. 为什么要有虚拟内存呢?🔍...

AJAX 数据库
AJAX 数据库 1. 引言 AJAX(Asynchronous JavaScript and XML)是一种流行的网络开发技术,它允许网页在不重新加载整个页面的情况下与服务器交换数据和更新部分网页内容。AJAX技术与数据库的结合,为现代网络应用提供了更加丰富和动态的用户体验。本文将探讨AJAX如何与数据库…...

力扣719.找出第K小的数对距离
力扣719.找出第K小的数对距离 二分答案 朴素版 双指针遍历数组 超过界限break auto check [&](int mid) -> bool{int res0;for(int i0;i<n-1;i)for(int ji1;j<n;j){if(nums[j] - nums[i] > mid) break;elseif(res > k) return true;}return false;};优…...

富格林:掌握可信出金交易策略
富格林认为,黄金市场是起起落落,似乎机遇无处不在,但很少有人能真正抓住机遇。黄金可以做多也可以做空,做空主要是为了从黄金价格波动的价差中获利。只有采用正规可信的操作技巧,才能实现顺利获利出金,减少…...
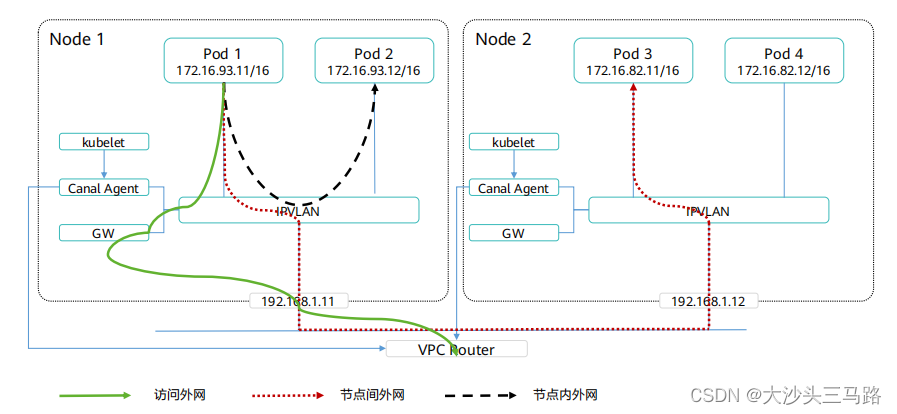
HCS-华为云Stack-容器网络
HCS-华为云Stack-容器网络 容器隧道overlay VPC网络...

【CSS in Depth2精译】1.1 层叠
CSS 本质上就是声明规则,并让这些特定的规则在各种情况下生效。一个类添加到某个元素上,则应用这个类包含的这一些样式;元素 X 是元素 Y 的一个子节点,则应用另一些样式。浏览器于是根据这些规则,判定所有样式生效的具…...

【读博日记】拓扑结构(待修正)
Topology 拓扑学 内容来源于互联网,还在甄别中——20240617 拓扑结构指把实体抽象成与其形状大小无关的点,把连接实体的线路抽象成线,再研究这些电线之间的关系。 所谓相似的拓扑结构: 例如一个圆环变成正方形、长方形、三角形…...
和setEnabled()的区别)
QT 中setVisible()和setEnabled()的区别
setVisible(bool)和setEnabled(true)在PyQt(以及其他类似的图形用户界面框架)中分别用于控制控件的可见性和可用性,它们之间的主要区别如下: setVisible(bool) 功能:这个函数用于设置QWidget控件的可见状态。参数&am…...

【YashanDB知识库】PHP使用ODBC使用数据库绑定参数功能异常
【问题分类】驱动使用 【关键字】ODBC、驱动使用、PHP 【问题描述】 PHP使用PDO_ODBC连接yashan数据库,使用绑定参数获取数据时,客户现场出现报错 本地复现未出现异常报错,但是无法正确获取数据。 【问题原因分析】开启ODBC报错日志后&am…...
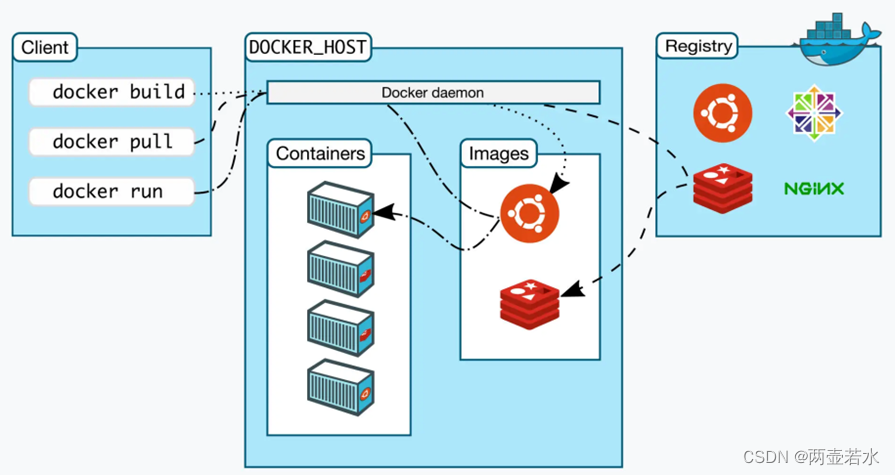
初级篇-Docker容器知识
Docker容器 容器主要是解决跨平台、跨服务运行环境的问题 容器将运行业务应用所需要的东西进行打包,包括依赖项、配置、脚本、二进制文件等。在容器中运行镜像,不用担心不同环境下运行不一致的问题。 容器本质上是一个特殊的进程,将资源、…...

【抽代复习笔记】19-群(十三):奇偶置换、循环置换的几个定理及例题
定义: ①在Sn中,能够表示为奇数多个对换乘积的置换称为“奇置换”,能够表示为偶数多个对换乘积的置换称为“偶置换”; ②所有偶置换的集合记为An。 例1:(1)计算S1和S2中奇、偶置换的数目&…...
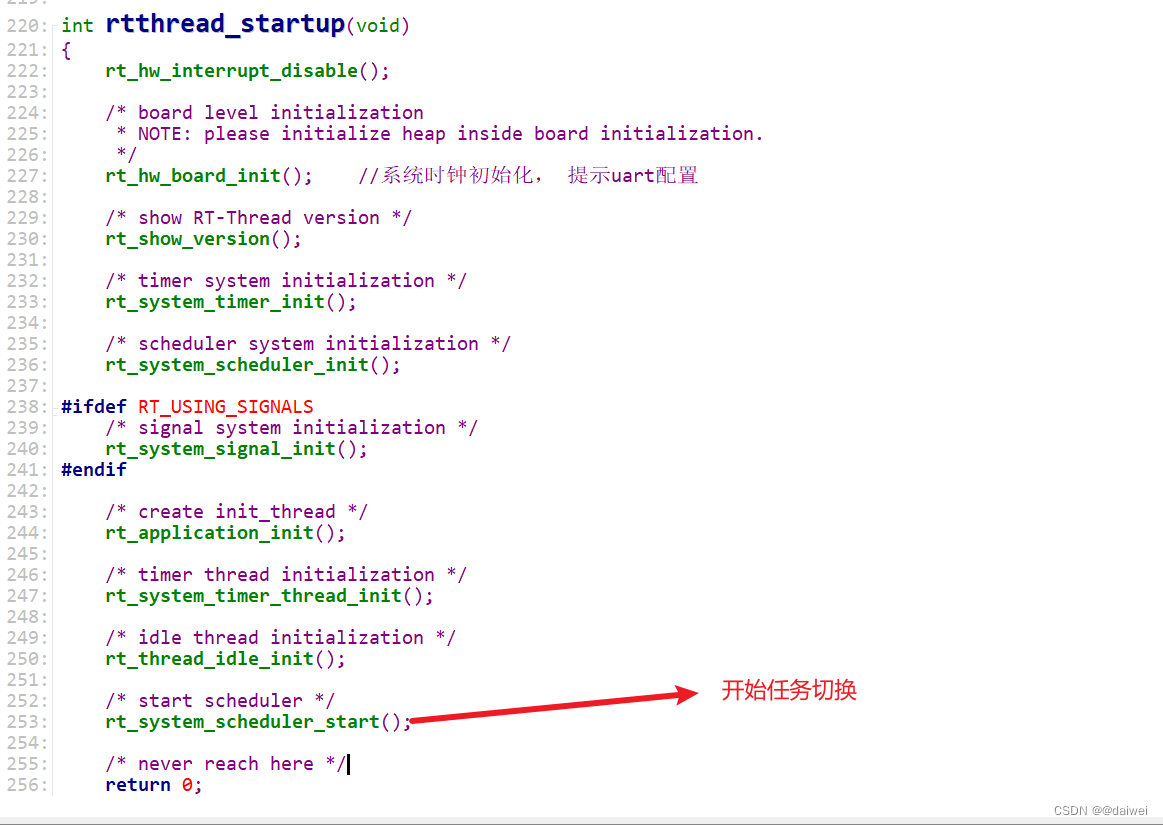
RT-Thread简介及启动流程分析
阅读引言: 最近在学习RT-Thread的内部机制,觉得这个启动流程和一些底层原理还是挺重要的, 所以写下此文。 目录 1, RT-Thread简介 2,RT-Thread任务的几种状态 3, 学习资源推荐 4, 启动流程分…...

前端导出带有合并单元格的列表
// 导出async function exportExcel(fileName "共识调整.xlsx") {// 所有数据const exportData await getAllMainData();// 表头内容let fitstTitleList [];const secondTitleList [];allColumns.value.forEach(column > {if (!column.children) {fitstTitleL…...

五年级数学知识边界总结思考-下册
目录 一、背景二、过程1.观察物体小学五年级下册“观察物体”知识点详解:由来、作用与意义**一、知识点核心内容****二、知识点的由来:从生活实践到数学抽象****三、知识的作用:解决实际问题的工具****四、学习的意义:培养核心素养…...

Java 加密常用的各种算法及其选择
在数字化时代,数据安全至关重要,Java 作为广泛应用的编程语言,提供了丰富的加密算法来保障数据的保密性、完整性和真实性。了解这些常用加密算法及其适用场景,有助于开发者在不同的业务需求中做出正确的选择。 一、对称加密算法…...

均衡后的SNRSINR
本文主要摘自参考文献中的前两篇,相关文献中经常会出现MIMO检测后的SINR不过一直没有找到相关数学推到过程,其中文献[1]中给出了相关原理在此仅做记录。 1. 系统模型 复信道模型 n t n_t nt 根发送天线, n r n_r nr 根接收天线的 MIMO 系…...

Springboot社区养老保险系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,社区养老保险系统小程序被用户普遍使用,为方…...

Docker 本地安装 mysql 数据库
Docker: Accelerated Container Application Development 下载对应操作系统版本的 docker ;并安装。 基础操作不再赘述。 打开 macOS 终端,开始 docker 安装mysql之旅 第一步 docker search mysql 》〉docker search mysql NAME DE…...

R语言速释制剂QBD解决方案之三
本文是《Quality by Design for ANDAs: An Example for Immediate-Release Dosage Forms》第一个处方的R语言解决方案。 第一个处方研究评估原料药粒径分布、MCC/Lactose比例、崩解剂用量对制剂CQAs的影响。 第二处方研究用于理解颗粒外加硬脂酸镁和滑石粉对片剂质量和可生产…...

【Redis】笔记|第8节|大厂高并发缓存架构实战与优化
缓存架构 代码结构 代码详情 功能点: 多级缓存,先查本地缓存,再查Redis,最后才查数据库热点数据重建逻辑使用分布式锁,二次查询更新缓存采用读写锁提升性能采用Redis的发布订阅机制通知所有实例更新本地缓存适用读多…...

华为OD机考-机房布局
import java.util.*;public class DemoTest5 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseSystem.out.println(solve(in.nextLine()));}}priv…...

Docker拉取MySQL后数据库连接失败的解决方案
在使用Docker部署MySQL时,拉取并启动容器后,有时可能会遇到数据库连接失败的问题。这种问题可能由多种原因导致,包括配置错误、网络设置问题、权限问题等。本文将分析可能的原因,并提供解决方案。 一、确认MySQL容器的运行状态 …...

