3.1. 马氏链-马氏链的定义和示例
马氏链的定义和示例
- 马氏链的定义和示例
- 1. 马氏链的定义
- 2. 马氏链的示例
- 2.1. 随机游走
- 2.2. 分支过程
- 2.3. Ehrenfest chain
- 2.4. 遗传模型
- 2.5. M/G/1 队列
马氏链的定义和示例
1. 马氏链的定义
对于可数状态空间的马氏链, 马氏性指的是给定当前状态, 其他过去的状态与未来的预测无关. 即对任意状态 i 0 , … i n − 1 , i i_{0}, \ldots i_{n-1}, i i0,…in−1,i, j j j
P ( X n + 1 = j ∣ X n = i , X n − 1 = i n − 1 , … X 0 = i 0 ) = P ( X n + 1 = j ∣ X n = i ) P\left(X_{n+1}=j \mid X_{n}=i, X_{n-1}=i_{n-1}, \ldots X_{0}=i_{0}\right)=P\left(X_{n+1}=j \mid X_{n}=i\right) P(Xn+1=j∣Xn=i,Xn−1=in−1,…X0=i0)=P(Xn+1=j∣Xn=i)
称条件概率 P ( X n + 1 = j ∣ X n = i ) P\left(X_{n+1}=j \mid X_{n}=i\right) P(Xn+1=j∣Xn=i)为马氏链 { X n , n = 0 , 1 , 2 , . . . } \{X_n,n=0,1,2,...\} {Xn,n=0,1,2,...}的一步转移概率, 简称转移概率, 记为 p i j p_{ij} pij, 表示处于状态 i i i的过程下一步转移到状态 j j j的概率.
2. 马氏链的示例
2.1. 随机游走
示例5.1.1 (随机游走的转移概率) 令 ξ 1 , ξ 2 , … ∈ Z d \xi_{1}, \xi_{2}, \ldots \in \mathbf{Z}^{d} ξ1,ξ2,…∈Zd独立, 分布为 μ \mu μ. X n = X 0 + ξ 1 + ⋯ + ξ n X_{n}=X_{0}+\xi_{1}+\cdots+\xi_{n} Xn=X0+ξ1+⋯+ξn, 其中 X 0 X_{0} X0是常数. 则 X n X_{n} Xn是马氏链,转移概率为 p ( i , j ) = μ ( { j − i } ) p(i, j)=\mu(\{j-i\}) p(i,j)=μ({j−i}).
证明: 证明 X n X_{n} Xn是马氏链. 若 μ j \mu_{j} μj是 ξ j \xi_{j} ξj的分布, 由于 X n X_n Xn和 ξ n + 1 \xi_{n+1} ξn+1独立, 则由示例4.1.7 (二元独立随机变量函数关于某变量的条件期望)
P ( X n + 1 ∈ B ∣ X n ) = P ( X n + ξ n + 1 ∈ B ∣ X n ) = μ n + 1 ( B − X n ) P\left(X_{n+1} \in B \mid X_{n}\right)=P\left(X_{n}+\xi_{n+1} \in B \mid X_{n}\right)=\mu_{n+1}\left(B-X_{n}\right) P(Xn+1∈B∣Xn)=P(Xn+ξn+1∈B∣Xn)=μn+1(B−Xn)
故 P ( X n + 1 ∈ B ∣ X n ) ∈ σ ( X n ) ⊂ F P\left(X_{n+1} \in B \mid X_{n}\right)\in \sigma(X_n)\subset \mathcal{F} P(Xn+1∈B∣Xn)∈σ(Xn)⊂F, 由定理4.1.12可得
P ( X n + 1 ∈ B ∣ X n ) = P ( X n + 1 ∈ B ∣ F n ) P\left(X_{n+1} \in B \mid X_{n}\right)=P\left(X_{n+1} \in B \mid \mathcal{F}_{n}\right) P(Xn+1∈B∣Xn)=P(Xn+1∈B∣Fn)
习题5.1.6 (以概率 θ \theta θ正向走, 1 − θ 1-\theta 1−θ负向走的随机游走是一个非时齐的马氏链) 令 θ , U 1 , U 2 , … \theta, U_{1}, U_{2}, \ldots θ,U1,U2,…是 ( 0 , 1 ) (0,1) (0,1)上的独立均匀分布. 若 U i ≤ θ U_{i} \leq \theta Ui≤θ, X i = 1 X_{i}=1 Xi=1; 若 U i > θ U_{i}>\theta Ui>θ, X i = − 1 X_{i}=-1 Xi=−1. S n = X 1 + ⋯ + X n S_{n}=X_{1}+\cdots+X_{n} Sn=X1+⋯+Xn.
- ( i ) (i) (i) 转移概率 P ( X n + 1 = 1 ∣ X 1 , … , X n ) P\left(X_{n+1}=1 \mid X_{1}, \ldots, X_{n}\right) P(Xn+1=1∣X1,…,Xn)只与 S n S_n Sn相关;
- ( i i ) (ii) (ii) S n S_{n} Sn是一个非时齐马尔可夫链. 自然, S n S_{n} Sn是一个估计 θ \theta θ的充分统计量.
证明:(i) 令 i 1 , … , i n ∈ { − 1 , 1 } i_{1}, \ldots, i_{n} \in\{-1,1\} i1,…,in∈{−1,1}, N = ∣ { m ≤ n : i m = 1 } ∣ N=\left|\left\{m \leq n: i_{m}=1\right\}\right| N=∣{m≤n:im=1}∣.
P ( X n + 1 = 1 ∣ X 1 = i 1 , … , X n = i n ) = P ( X 1 = i 1 , … , X n = i n , X n + 1 = 1 ) P ( X 1 = i 1 , … , X n = i n ) ( 重期望公式 ) = ∫ θ N + 1 ( 1 − θ ) n − N d θ ∫ θ N ( 1 − θ ) n − N d θ = ( S n / 2 + n / 2 + 1 ) ! / ( n + 2 ) ! ( S n / 2 + n / 2 ) ! / ( n + 1 ) ! = S n + n + 2 2 n + 4 \begin{aligned} P\left(X_{n+1}=1 \mid X_{1}=i_{1}, \ldots, X_{n}=i_{n}\right)&=\frac{P\left(X_{1}=i_{1}, \ldots, X_{n}=i_{n}, X_{n+1}=1\right)}{P\left(X_{1}=i_{1}, \ldots, X_{n}=i_{n}\right)}\\ (\text{重期望公式})&=\frac{\int \theta^{N+1}(1-\theta)^{n-N} d \theta}{\int \theta^{N}(1-\theta)^{n-N} d \theta}\\ &=\frac{\left(S_{n}/2+n/2+1\right) ! /(n+2) !}{(S_{n}/2+n/2)! /(n+1) !}=\frac{S_{n}+n+2}{2n+4} \end{aligned} P(Xn+1=1∣X1=i1,…,Xn=in)(重期望公式)=P(X1=i1,…,Xn=in)P(X1=i1,…,Xn=in,Xn+1=1)=∫θN(1−θ)n−Ndθ∫θN+1(1−θ)n−Ndθ=(Sn/2+n/2)!/(n+1)!(Sn/2+n/2+1)!/(n+2)!=2n+4Sn+n+2
上式由 ∫ 0 1 x m ( 1 − x ) k d x = m ! k ! / ( m + k + 1 ) ! \int_{0}^{1} x^{m}(1-x)^{k} d x=m ! k ! /(m+k+1) ! ∫01xm(1−x)kdx=m!k!/(m+k+1)!得到.
习题5.1.1. i.i.d序列取值数量序列是马氏链 . 令 ξ 1 , ξ 2 , … ∈ { 1 , 2 , … , N } \xi_{1}, \xi_{2}, \ldots\in\{1,2, \ldots, N\} ξ1,ξ2,…∈{1,2,…,N} i.i.d, 各点取值概率 1 / N 1 / N 1/N. 证明 X n = ∣ { ξ 1 , … , ξ n } ∣ X_{n}=\left|\left\{\xi_{1}, \ldots, \xi_{n}\right\}\right| Xn=∣{ξ1,…,ξn}∣是马氏链, 并计算转移概率.
证明: X n + 1 X_{n+1} Xn+1依赖于 X n X_{n} Xn和 ξ n + 1 \xi_{n+1} ξn+1, 自然是马氏链. 转移概率可以表示为:
p ( k , k + 1 ) = 1 − k N , p ( k , k ) = k N , p ( i , j ) = 0 其他 p(k, k+1)=1-\frac{k}{N}, \quad p(k, k)=\frac{k}{N}, \quad p(i, j)=0 \text {其他} p(k,k+1)=1−Nk,p(k,k)=Nk,p(i,j)=0其他
习题5.1.2.对称随机游走最大值序列不是马氏链 S 0 = 0 , S n = ξ 1 + ⋯ ξ n S_{0}=0, S_{n}=\xi_{1}+\cdots \xi_{n} S0=0,Sn=ξ1+⋯ξn是对称随机游走, X n = max { S m : 0 ≤ m ≤ n } X_{n}=\max \left\{S_{m}: 0 \leq m \leq n\right\} Xn=max{Sm:0≤m≤n}. X n X_{n} Xn不是马氏链.
证明:当 X n = m , X n − 1 = m − 1 X_{n}=m,X_{n-1}=m-1 Xn=m,Xn−1=m−1, 则 X n = S n X_n=S_n Xn=Sn, 故
P ( X n + 1 = m + 1 ∣ X n = m , X n − 1 = m − 1 ) = 1 / 2 \mathbb{P}\left(X_{n+1}=m+1 \mid X_{n}=m, X_{n-1}=m-1\right)=1/2 P(Xn+1=m+1∣Xn=m,Xn−1=m−1)=1/2
当 X n = m , X n − 1 = m X_{n}=m,X_{n-1}=m Xn=m,Xn−1=m, P ( X n + 1 = m + 1 ∣ X n = m , X n − 1 = m ) = 0 \mathbb{P}\left(X_{n+1}=m+1 \mid X_{n}=m, X_{n-1}=m\right)=0 P(Xn+1=m+1∣Xn=m,Xn−1=m)=0, X n X_{n} Xn非马氏链.
2.2. 分支过程
示例 5.1.2 (分支过程的转移概率) S = { 0 , 1 , 2 , … } S=\{0,1,2, \ldots\} S={0,1,2,…}, 第 n n n代每个个体 i i i产生i.i.d的后代数 ξ 1 , ξ 2 , … \xi_{1}, \xi_{2}, \ldots ξ1,ξ2,…, 则 p ( i , j ) = P ( ∑ m = 1 i ξ m = j ) p(i, j)=P(\sum_{m=1}^{i} \xi_{m}=j) p(i,j)=P(∑m=1iξm=j), .
2.3. Ehrenfest chain
示例 5.1.3 (Ehrenfest chain) 第一个瓮有 k k k个球, 第二个瓮有 r − k r-k r−k个, 随机挑选一个球移到另一个瓮中. 令 S = { 0 , 1 , … , r } S=\{0,1, \ldots, r\} S={0,1,…,r}, 第一个瓮中球数的转移概率为
p ( k , k + 1 ) = ( r − k ) / r , p ( k , k − 1 ) = k / r , p ( i , j ) = 0 否则 , p(k, k+1)=(r-k) / r, p(k, k-1)=k / r, p(i, j)=0 \quad \text {否则 }, p(k,k+1)=(r−k)/r,p(k,k−1)=k/r,p(i,j)=0否则 ,Ehrenfest用此模拟两个腔室(大小形状相同,一个小孔连接)间空气分子的划分.
习题5.1.5. 假设左瓮和右瓮, 每个瓮 m m m个球. b b b ( ≤ m \leq m ≤m ) 个黑色球, 2 m − b 2 m-b 2m−b个白色球. 每次从每个瓮中选择一个球然后互相交换. 计算左瓮黑球数的转移概率.
证明: p ( n , n + 1 ) = m − n m ⋅ b − n m , p ( n , n − 1 ) = n m ⋅ m + n − b m p(n, n+1) =\frac{m-n}{m} \cdot \frac{b-n}{m},p(n, n-1) =\frac{n}{m} \cdot \frac{m+n-b}{m} p(n,n+1)=mm−n⋅mb−n,p(n,n−1)=mn⋅mm+n−b
2.4. 遗传模型
示例 5.1.4 (Wright–Fisher遗传模型) 设总体中的个体数为 N N N, 每个个体的基因按基因 A A A 的基因频率的大小, 在下一代中转移成为基因 A A A.
换句话说, 如果在第 n n n代母体中基因 A A A出现了 i i i次, 基因 a a a出现了 N − i N-i N−i次, 则下一代出现基因 A A A的概率为 p i = i N p_{i}=\frac{i}{N} pi=Ni, 而出现基因 a a a 的概率为 1 − p i 1-p_{i} 1−pi.
- (i) 令 X n X_n Xn表示第 n n n代基因 A A A出现的次数, 计算 p i j = P { X n + 1 = j ∣ X n = i } p_{i j}=P\left\{X_{n+1}=j \mid X_{n}=i\right\} pij=P{Xn+1=j∣Xn=i}.
- (ii) 引入变异, 即 A A A在下一代有概率 μ \mu μ是 a a a, 而 a a a在下一代有概率 ν \nu ν是 A A A.
证明:(i) 记 X n X_{n} Xn 为第 n n n 代中携带基因 A A A 的个体数, 则易知 { X n } \left\{X_{n}\right\} {Xn} 是一个状态空间为 S = { 0 , 1 , ⋯ , N } S=\{0,1, \cdots, N\} S={0,1,⋯,N} 的时齐Markov链, 其转移概率矩阵为 P = ( p i j ) \boldsymbol{P}=\left(p_{i j}\right) P=(pij), 其中
p i j = P { X n + 1 = j ∣ X n = i } = C N j p i j ( 1 − p i ) N − j = C N j ( i N ) j ( 1 − i N ) N − j p_{i j}=P\left\{X_{n+1}=j \mid X_{n}=i\right\}=\mathrm{C}_{N}^{j} p_{i}^{j}\left(1-p_{i}\right)^{N-j}=\mathrm{C}_{N}^j\left(\frac{i}{ N}\right)^{j}\left(1-\frac{i}{N}\right)^{N-j} pij=P{Xn+1=j∣Xn=i}=CNjpij(1−pi)N−j=CNj(Ni)j(1−Ni)N−j
在这个模型中,状态 X = 0 X=0 X=0和 N N N对应于总体是 A A A和 a a a,称为吸收状态 (absorbing states), 即 p ( x , x ) = 1 p(x,x)=1 p(x,x)=1. 这个链最终将进入状态 0 0 0或状态 N N N.
(ii) 产生 A A A的概率是 ρ i = ( i / N ) ( 1 − u ) + ( N − i / N ) v \rho_{i}=({i}/{N})(1-u)+({N-i}/{N}) v ρi=(i/N)(1−u)+(N−i/N)v. 转移概率为
p ( i , j ) = ( N j ) ( ρ i ) j ( 1 − ρ i ) N − j p(i, j)=\left(\begin{array}{c} N \\ j \end{array}\right)\left(\rho_{i}\right)^{j}\left(1-\rho_{i}\right)^{N-j} p(i,j)=(Nj)(ρi)j(1−ρi)N−j
如果 u u u和 v v v都是正的, 0 0 0和 N N N就不再是吸收态了,系统可收敛到一个平衡分布.
习题5.1.3 (连续成对的抛硬币序列). 令 ξ 0 , ξ 1 , … ∈ { H , T } \xi_{0}, \xi_{1}, \ldots\in\{H, T\} ξ0,ξ1,…∈{H,T}独立同分布, 每个取值概率为 1 / 2 1 / 2 1/2 (硬币正反面). X n = ( ξ n , ξ n + 1 ) X_{n}=\left(\xi_{n}, \xi_{n+1}\right) Xn=(ξn,ξn+1)是一个马氏链, 计算转移概率 p p p以及 p 2 p^{2} p2.
证明:由于 X n = ( ξ n , ξ n + 1 ) X_{n}=\left(\xi_{n}, \xi_{n+1}\right) Xn=(ξn,ξn+1), 可知 X n − 2 = ( ξ n − 2 , ξ n − 1 ) , ⋯ , X 0 = ( ξ 0 , ξ 1 ) X_{n-2}=\left(\xi_{n-2}, \xi_{n-1}\right), \cdots, X_{0}=\left(\xi_{0}, \xi_{1}\right) Xn−2=(ξn−2,ξn−1),⋯,X0=(ξ0,ξ1)与 X n X_{n} Xn独立,因此 X n X_{n} Xn是马氏链. 易计算得到转移概率 p p p及 p 2 p^{2} p2.
习题5.1.4 (兄弟姐妹结对遗传). 两只动物交配的直系后代中随机选择两个异性个体交配, 过程持续. 假设个体是 A A , A a , a a AA,Aa,aa AA,Aa,aa中的一个, 从每个父母中选择一个字母来决定后代类型, 计算第 n n n代基因型对的转移概率.
证明:该马氏链第 n n n代基因型对共有以下6个状态, 易计算转移概率
A A , A A A A , A a A A , a a A a , A a A a , a a a a , a a A A, A A \quad A A, A a \quad A A, a a \quad A a, A a \quad A a, a a \quad a a, a a AA,AAAA,AaAA,aaAa,AaAa,aaaa,aa
2.5. M/G/1 队列
示例5.1.5. M/G/1 队列:客户 n n n开始服务的队列人数 客户按照速率为 λ \lambda λ的泊松过程到达. 不相交时间间隔内的到达数独立,每个客户服务时长独立,分布为 F F F.
设 X n X_n Xn为第 n n n个客户进入服务时队列的客户数(包括服务中的客户). X 0 = x X_0=x X0=x表示客户 0 0 0刚开始服务时队列有 x x x人. 计算 X n X_n Xn的转移概率.
证明:在一个服务时间内 k k k个顾客到达的概率为 a k a_k ak
a k = ∫ 0 ∞ e − λ t ( λ t ) k k ! d F ( t ) a_{k}=\int_{0}^{\infty} e^{-\lambda t} \frac{(\lambda t)^{k}}{k !} d F(t) ak=∫0∞e−λtk!(λt)kdF(t)
令 ξ i \xi_{i} ξi表示第 i i i次服务时间内到达的客户数减去完成服务的1个客户, 则 ξ 1 , ξ 2 , … \xi_{1}, \xi_{2}, \ldots ξ1,ξ2,…独立同分布, 且 P ( ξ i = k − 1 ) = a k P\left(\xi_{i}=k-1\right)=a_{k} P(ξi=k−1)=ak. 可得 X n + 1 = ( X n + ξ n + 1 ) + X_{n+1}=\left(X_{n}+\xi_{n+1}\right)^{+} Xn+1=(Xn+ξn+1)+ (正部分仅在 X n = 0 X_n=0 Xn=0和 ξ n + 1 = − 1 \xi_{n+1}=−1 ξn+1=−1时生效).
很容易看出,序列 ξ i \xi_{i} ξi是一个具有如下转移概率的马尔可夫链
p ( 0 , 0 ) = a 0 + a 1 , p ( j , j − 1 + k ) = a k 若 j ≥ 1 或 k > 1 p(0,0)=a_{0}+a_{1},p(j, j-1+k)=a_{k} \quad \text {若 } j \geq 1 \text { 或} k>1 p(0,0)=a0+a1,p(j,j−1+k)=ak若 j≥1 或k>1其中, a k a_{k} ak形式复杂但不重要,可以假设 a k > 0 , k ≥ 0 a_{k}>0, k \geq 0 ak>0,k≥0且 ∑ k > 0 a k = 1 \sum_{k>0} a_{k}=1 ∑k>0ak=1.
相关文章:

3.1. 马氏链-马氏链的定义和示例
马氏链的定义和示例 马氏链的定义和示例1. 马氏链的定义2. 马氏链的示例2.1. 随机游走2.2. 分支过程2.3. Ehrenfest chain2.4. 遗传模型2.5. M/G/1 队列 马氏链的定义和示例 1. 马氏链的定义 对于可数状态空间的马氏链, 马氏性指的是给定当前状态, 其他过去的状态与未来的预测…...
红利之外的A股底仓选择:A50
内容提要 华泰证券指出,当前指数层面下行风险不大,市场再入震荡期下,可关注三条配置线索:1)A50为代表的产业巨头;2)以家电/食饮/物流/出版为代表的稳健消费龙头,3)消费电…...

wondershaper 一款限制 linux 服务器网卡级别的带宽工具
文章目录 一、关于wondershaper二、文档链接三、源码下载四、限流测试五、常见报错1. /usr/local/sbin/wondershaper: line 145: tc: command not found2. Failed to download metadata for repo ‘appstream‘: Cannot prepare internal mirrorlist: No URLs.. 一、关于wonder…...

独孤思维:盲目进群,根本赚不到钱
01 我看有些伙伴,对标同行找写作素材和灵感的时候。 喜欢把对标文章发给ai提炼总结。 这个方法好是好,但是,有一个问题。 即,无法感受全文的细节。 更无法感受作者的情感和温度。 就好像电影《记忆大师》一样。 我提取了记…...
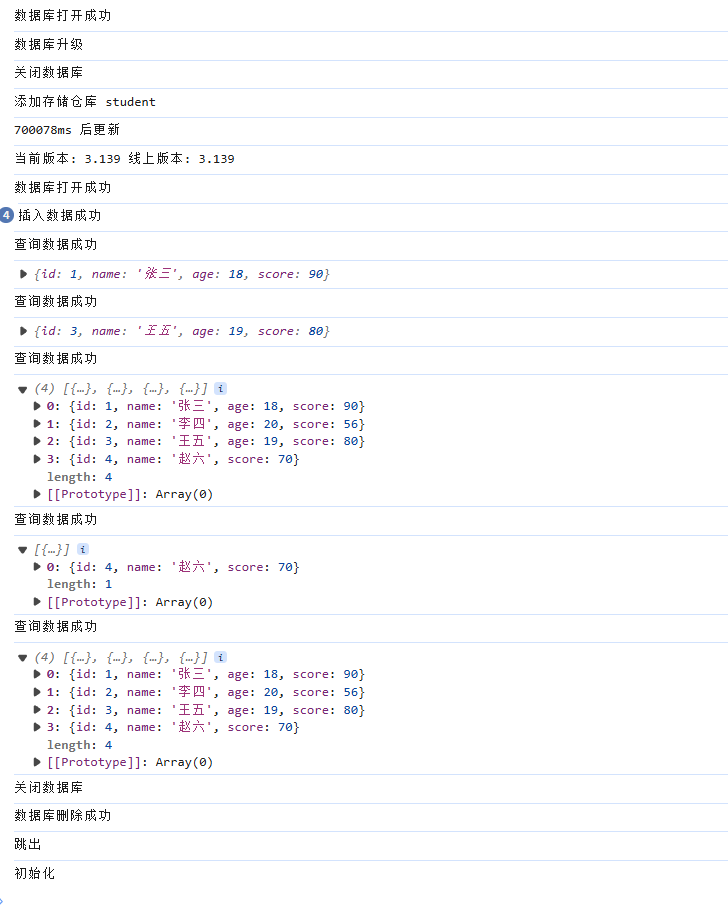
针对indexedDB的简易封装
连接数据库 我们首先创建一个DBManager类,通过这个类new出来的对象管理一个数据库 具体关于indexedDB的相关内容可以看我的这篇博客 indexedDB class DBManager{}我们首先需要打开数据库,打开数据库需要数据库名和该数据库的版本 constructor(dbName,…...
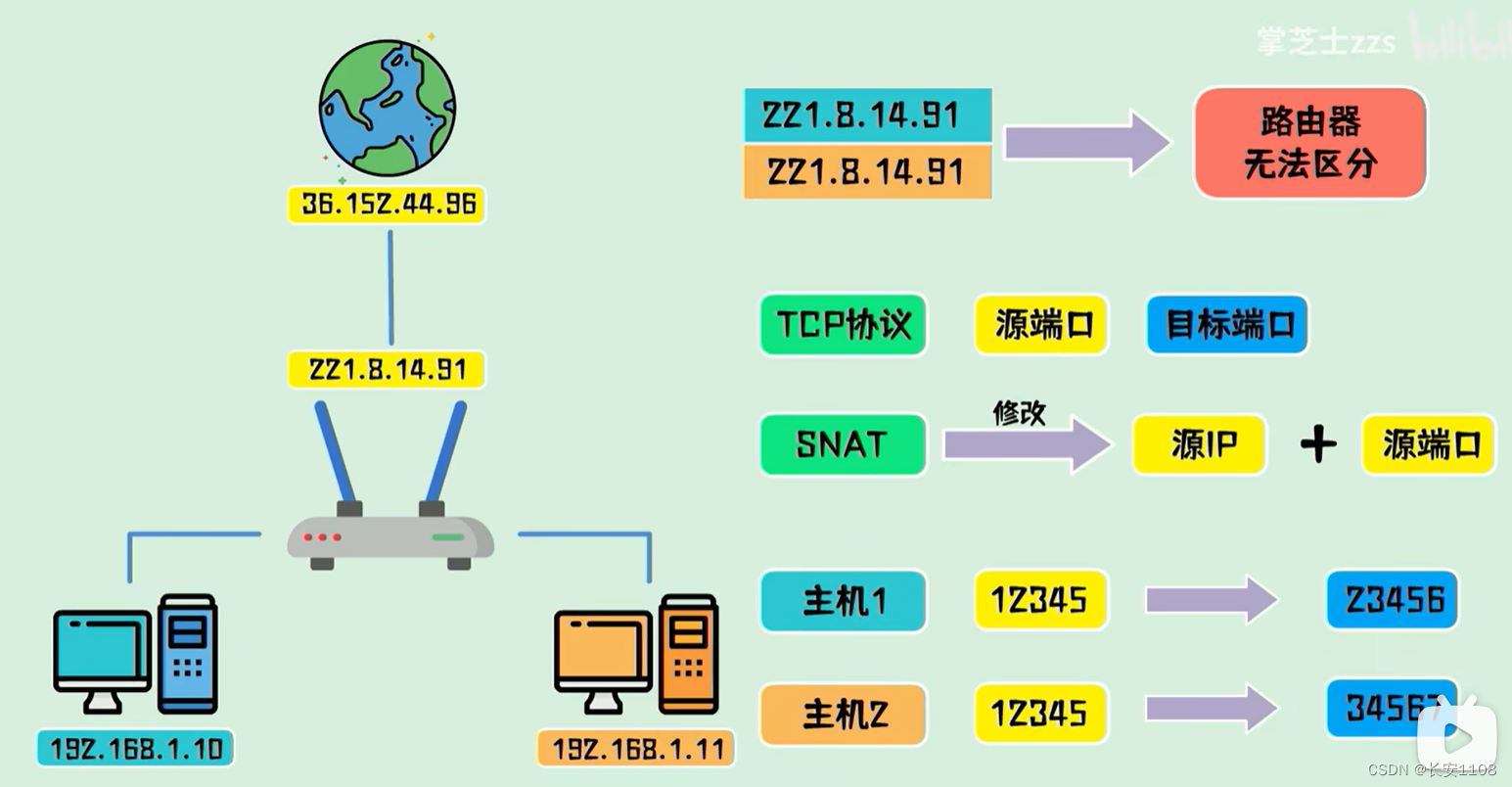
网络编程--网络理论基础(二)
这里写目录标题 网络通信流程mac地址、ip地址arp协议交换机路由器简介子网划分网关 路由总结 为什么ip相同的主机在与同一个互联网服务通信时不冲突公网ip对于同一个路由器下的不同设备,虽然ip不冲突,但是因为都是由路由器的公网ip转发通信,接…...

Python MongoDB 基本操作
本文内容主要为使用Python 对Mongodb数据库的一些基本操作整理。 目录 安装类库 操作实例 引用类库 连接服务器 连接数据库 添加文档 添加单条 批量添加 查询文档 查询所有文档 查询部分文档 使用id查询 统计查询 排序 分页查询 更新文档 update_one方法 upd…...

Node.js 入门:
Node.js 是一个开源、跨平台的 JavaScript 运行时环境,它允许开发者在浏览器之外编写命令行工具和服务器端脚本。以下是一些关于 Node.js 的基础教程: 1. **Node.js 入门**: - 了解 Node.js 的基本概念,包括它是一个基于 Chro…...
)
java8 List的Stream流操作 (实用篇 三)
目录 java8 List的Stream流操作 (实用篇 三) 初始数据 1、Stream过滤: 过滤-常用方法 1.1 筛选单元素--年龄等于18 1.2 筛选单元素--年龄大于18 1.3 筛选范围--年龄大于18 and 年龄小于40 1.4 多条件筛选--年龄大于18 or 年龄小于40 and sex男 1.5 多条件筛…...

机器学习python实践——数据“相关性“的一些补充性个人思考
在上一篇“数据白化”的文章中,说到了数据“相关性”的概念,但是在统计学中,不仅存在“相关性”还存在“独立性”等等,所以,本文主要对数据“相关性”进行一些补充。当然,如果这篇文章还能入得了各位“看官…...

MySQL——触发器(trigger)基本结构
1、修改分隔符符号 delimiter $$ $$可以修改 2、创建触发器函数名称 create trigger 函数名 3、什么样在操作触发,操作哪个表 after :……之后触发 before :……之后触发 insert :……之后触发 update :……之后触…...

数字孪生定义及应用介绍
数字孪生定义及应用介绍 1 数字孪生(Digital Twin, DT)概述1.1 定义1.2 功能1.3 使用场景1.4 数字孪生三步走1.4.1 数字模型1.4.2 数字影子1.4.3 数字孪生 数字孪生地球平台Earth-2 参考 1 数字孪生(Digital Twin, DT)概述 数字孪…...
——体系:数据清洗——技术方法、主要工具)
数据赋能(122)——体系:数据清洗——技术方法、主要工具
技术方法 数据清洗标准模型是将数据输入到数据清洗处理器,通过一系列步骤“清理”数据,然后以期望的格式输出清理过的数据。数据清洗从数据的准确性、完整性、一致性、惟一性、适时性、有效性几个方面来处理数据的丢失值、越界值、不一致代码、重复数据…...

【SCAU数据挖掘】数据挖掘期末总复习题库简答题及解析——中
1. 某学校对入学的新生进行性格问卷调查(没有心理学家的参与),根据学生对问题的回答,把学生的性格分成了8个类别。请说明该数据挖掘任务是属于分类任务还是聚类任务?为什么?并利用该例说明聚类分析和分类分析的异同点。 解答: (a)该数据…...

2024年注册安全工程师报名常见问题汇总!
注册安全工程师报名 24年注册安全工程师报名已正式拉开序幕,报名时间为6月18日—7月10日,考试时间为10月26日—10月27日。 目前经有12个地区公布了2024年注册安全工程师报名时间: 注册安全工程师报名信息完善 根据注安报名系统提示&am…...

JRebel-JVMTI [FATAL] Couldn‘t write to C:\Users\中文用户名-完美解决
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 热部署下载参考博客解决第一步第二步第三步:第四步: 热部署下载 下载后启动报错:JRebel-JVMTI [FATAL] Couldn’t write to C:\…...

STM32基于DMA数据转运和AD多通道
文章目录 1. DMA数据转运 1.1 初始化DMA步骤 1.2 DMA的库函数 1.3 设置当前数据寄存器 1.4 DMA获取当前数据寄存器 2. DMA数据转运 2.1 DMA.C 2.2 DMA.H 2.3 MAIN.C 3. DMAAD多通道 3.1 AD.C 3.2 AD.H 3.3 MAIN.C 1. DMA数据转运 对于DMA的详细解析可以看下面这篇…...

安卓应用开发——Android Studio中通过id进行约束布局
在Android开发中,布局通常使用XML文件来描述,而约束(如相对位置、大小等)可以通过多种方式实现,但直接使用ID进行约束并不直接对应于Android的传统布局系统(如LinearLayout、RelativeLayout等)。…...

Elasticsearch过滤器(filter):原理及使用
Hi~!这里是奋斗的小羊,很荣幸您能阅读我的文章,诚请评论指点,欢迎欢迎 ~~ 💥💥个人主页:奋斗的小羊 💥💥所属专栏:C语言 🚀本系列文章为个人学习…...

Docker配置与使用详解
一、引言 随着云计算和微服务的兴起,Docker作为一种轻量级的容器化技术,越来越受到开发者和运维人员的青睐。Docker通过容器化的方式,将应用程序及其依赖项打包成一个可移植的镜像,从而实现了应用程序的快速部署和扩展。本文将详…...
)
【位运算】消失的两个数字(hard)
消失的两个数字(hard) 题⽬描述:解法(位运算):Java 算法代码:更简便代码 题⽬链接:⾯试题 17.19. 消失的两个数字 题⽬描述: 给定⼀个数组,包含从 1 到 N 所有…...

【第二十一章 SDIO接口(SDIO)】
第二十一章 SDIO接口 目录 第二十一章 SDIO接口(SDIO) 1 SDIO 主要功能 2 SDIO 总线拓扑 3 SDIO 功能描述 3.1 SDIO 适配器 3.2 SDIOAHB 接口 4 卡功能描述 4.1 卡识别模式 4.2 卡复位 4.3 操作电压范围确认 4.4 卡识别过程 4.5 写数据块 4.6 读数据块 4.7 数据流…...

Auto-Coder使用GPT-4o完成:在用TabPFN这个模型构建一个预测未来3天涨跌的分类任务
通过akshare库,获取股票数据,并生成TabPFN这个模型 可以识别、处理的格式,写一个完整的预处理示例,并构建一个预测未来 3 天股价涨跌的分类任务 用TabPFN这个模型构建一个预测未来 3 天股价涨跌的分类任务,进行预测并输…...

2.Vue编写一个app
1.src中重要的组成 1.1main.ts // 引入createApp用于创建应用 import { createApp } from "vue"; // 引用App根组件 import App from ./App.vue;createApp(App).mount(#app)1.2 App.vue 其中要写三种标签 <template> <!--html--> </template>…...

全球首个30米分辨率湿地数据集(2000—2022)
数据简介 今天我们分享的数据是全球30米分辨率湿地数据集,包含8种湿地亚类,该数据以0.5X0.5的瓦片存储,我们整理了所有属于中国的瓦片名称与其对应省份,方便大家研究使用。 该数据集作为全球首个30米分辨率、覆盖2000–2022年时间…...

第25节 Node.js 断言测试
Node.js的assert模块主要用于编写程序的单元测试时使用,通过断言可以提早发现和排查出错误。 稳定性: 5 - 锁定 这个模块可用于应用的单元测试,通过 require(assert) 可以使用这个模块。 assert.fail(actual, expected, message, operator) 使用参数…...

【android bluetooth 框架分析 04】【bt-framework 层详解 1】【BluetoothProperties介绍】
1. BluetoothProperties介绍 libsysprop/srcs/android/sysprop/BluetoothProperties.sysprop BluetoothProperties.sysprop 是 Android AOSP 中的一种 系统属性定义文件(System Property Definition File),用于声明和管理 Bluetooth 模块相…...

【单片机期末】单片机系统设计
主要内容:系统状态机,系统时基,系统需求分析,系统构建,系统状态流图 一、题目要求 二、绘制系统状态流图 题目:根据上述描述绘制系统状态流图,注明状态转移条件及方向。 三、利用定时器产生时…...

前端开发面试题总结-JavaScript篇(一)
文章目录 JavaScript高频问答一、作用域与闭包1.什么是闭包(Closure)?闭包有什么应用场景和潜在问题?2.解释 JavaScript 的作用域链(Scope Chain) 二、原型与继承3.原型链是什么?如何实现继承&a…...
Mobile ALOHA全身模仿学习
一、题目 Mobile ALOHA:通过低成本全身远程操作学习双手移动操作 传统模仿学习(Imitation Learning)缺点:聚焦与桌面操作,缺乏通用任务所需的移动性和灵活性 本论文优点:(1)在ALOHA…...
