编程入门笔记:从基础到进阶的探索之旅
编程入门笔记:从基础到进阶的探索之旅
编程,作为现代科技的基石,正日益渗透到我们生活的方方面面。对于初学者来说,掌握编程技能不仅有助于提升解决问题的能力,还能开启通往创新世界的大门。本篇文章将从四个方面、五个方面、六个方面和七个方面,带你走进编程的奇妙世界。
四个方面:编程基础概念与语法
编程之旅始于对基础概念与语法的理解。我们需要了解什么是变量、数据类型、控制结构等基本元素,并掌握它们的用法。同时,我们还要学习不同编程语言的语法规则,如Python的缩进规则、Java的类与对象等。这些基础知识将为我们后续的编程实践奠定坚实的基础。
五个方面:算法与数据结构
算法和数据结构是编程的核心。我们需要学习各种经典算法,如排序、查找等,并理解它们的工作原理和适用场景。同时,我们还要掌握常见的数据结构,如数组、链表、栈和队列等,以便在解决实际问题时能够灵活运用。
六个方面:编程实践与项目经验
理论知识固然重要,但实践才是检验真理的唯一标准。我们需要通过编写简单的程序、参与开源项目或自主开发小应用等方式,不断积累编程实践经验。在实践中,我们会遇到各种问题和挑战,但正是这些经历让我们不断成长和进步。
m.yzsfs.com
wap.yzsfs.com
blog.yzsfs.com
www.teec.yzsfs.com
www.x.yzsfs.com
www.a.yzsfs.com
m.j.yzsfs.com
七个方面:持续学习与进阶提升
编程是一个不断学习和进步的过程。随着技术的不断发展,新的编程语言和框架层出不穷。我们需要保持对新技术的好奇心和学习热情,不断拓宽自己的知识边界。同时,我们还要学会总结和反思自己的编程经验,从中提取经验教训,为未来的进阶提升做好准备。
综上所述,编程入门是一个充满挑战和乐趣的过程。通过掌握基础概念与语法、算法与数据结构、编程实践与项目经验以及持续学习与进阶提升等方面的知识,我们可以逐步提升自己的编程能力,并在未来的科技领域中展现出自己的才华和创造力。让我们一起踏上这趟编程之旅吧!
相关文章:

编程入门笔记:从基础到进阶的探索之旅
编程入门笔记:从基础到进阶的探索之旅 编程,作为现代科技的基石,正日益渗透到我们生活的方方面面。对于初学者来说,掌握编程技能不仅有助于提升解决问题的能力,还能开启通往创新世界的大门。本篇文章将从四个方面、五…...

小规模自建 Elasticsearch 的部署及优化
本文将详细介绍如何在 CentOS 7 操作系统上部署并优化 Elasticsearch 5.3.0,以承载千万级后端服务的数据采集。要使用Elasticsearch至少需要三台独立的服务器,本文所用服务器配置为4核8G的ECS云服务器,其中一台作为 master + data 节点、一台作为 client + data 节点、最后一…...
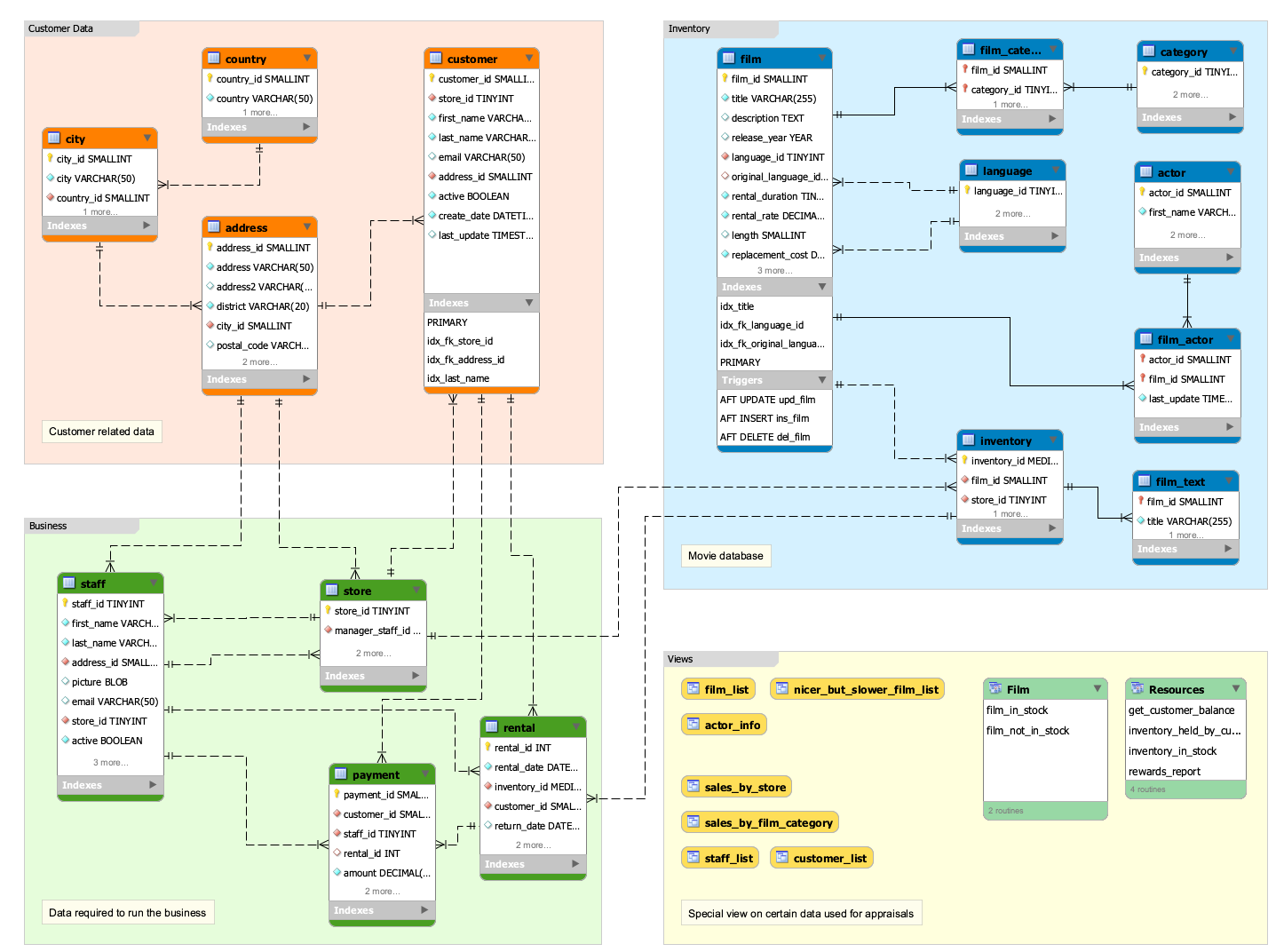
MySQL 示例数据库大全
前言: 我们练习 SQL 时,总会自己创造一些测试数据或者网上找些案例来学习,其实 MySQL 官方提供了好几个示例数据库,在 MySQL 的学习、开发和实践中具有非常重要的作用,能够帮助初学者更好地理解和应用 MySQL 的各种功…...
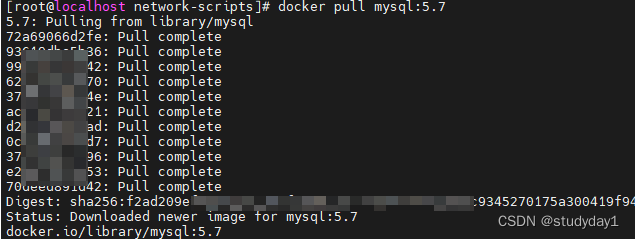
VirtualBox、Centos7下安装docker后pull镜像问题、ftp上传文件问题
Docker安装篇(CentOS7安装)_docker 安装 centos7-CSDN博客 首先,安装docker可以根据这篇文章进行安装,安装完之后,我们就需要去通过docker拉取相关的服务镜像,然后安装相应的服务容器,比如我们通过docker来安装mysql,…...

链表 题目汇总
237. 删除链表中的节点...

grafana连接influxdb2.x做数据大盘
连接influxdb 展示数据 新建仪表盘 选择存储库 设置展示...

Java证件识别中的身份证识别接口
现如今,越来越多的互联网应用需要对身份证进行实名认证,但不知道大家有没有发现,从最初的手动录入身份证信息转变到了现在的图片上传自动识别呢?其实,这都是因为集成了身份证识别接口功能,今天,…...

迷你小风扇哪个品牌好?迷你小风扇前十名公开揭晓!
随着夏日的炎热袭来,迷你小风扇成为了许多人随身携带的清凉利器。无论是在办公室、户外活动,还是在旅行途中,迷你小风扇都以其小巧便携、强劲风力和持久续航的优势,迅速俘获了大批用户的喜爱。然而,市面上迷你小风扇品…...
MikroTik RouterOS 授权签名验证分析
MikroTik 软路由 百科https://baike.baidu.com/item/mikrotik/9776775官网https://mikrotik.com/ 授权文件分析 -----BEGIN MIKROTIK SOFTWARE KEY------------ mr3jH5qhn9irtF53ZICFTN7Tk7wIx7ZkxdAxJ19ydASY ShhFteHMntBTyaS8wuNdIJJPidJxbuNPLTvCsv7zLA …...
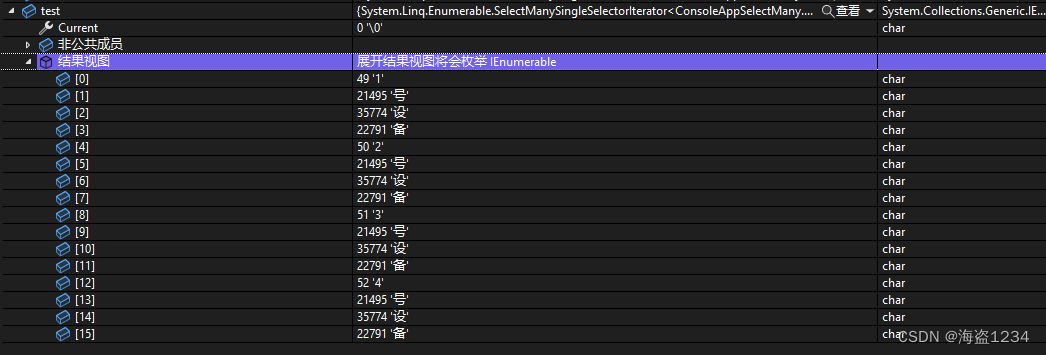
C#开发-集合使用和技巧(六)特殊转换方法SelectMany的介绍和用法
介绍 SelectMany 方法在C#中用于将集合中的元素转换为其他类型的集合,并将这些集合扁平化为一个单一的序列。它是LINQ的一部分,允许你在一个序列上进行投影和过滤操作,然后将结果合并成一个序列。 方法定义 public static IEnumerable<…...

高考后的抉择:如何在心仪专业与知名学校之间做出选择?
目录 前言1. 专业选择的深度探讨1.1 专业的优势与挑战1.1.1 课程学习1.1.2 就业前景 1.2 专业选择的个人经验与思考 2. 名校对个人发展的长短期影响2.1 名校声誉的品牌效应2.1.1 职业发展2.1.2 社会认可度 2.2 教育资源与学术氛围2.2.1 教育资源2.2.2 学术氛围 2.3 就业优势 3.…...

黄仁勋提到的机器人世界,还需要AI数据来“调教” | CVPR 2024
本周,CVPR 2024正在美国西雅图拉开序幕。今年CVPR论文投稿数再次创下新纪录,可想而知本届会议的火热。 从研究主题来看,具身智能这一大热点值得关注。 黄仁勋在COMPUTEX大会开幕前夕的演讲中预言:AI的下一个浪潮将是物理AI。 即…...

语言中 函数用地址传参的好处
在C语言中,使用地址传参(传递指针)有以下几个好处: 1. **减少内存开销**: - 传递一个指针(通常是一个地址)比传递一个大的结构体或数组要高效得多,因为指针通常是一个固定大小&a…...

Python进阶二: NumPy基础:数组和矢量计算
二、NumPy基础:数组和矢量计算 本文源自微博客(www.microblog.store),且以获得授权 NumPy(Numerical Python的简称)是Python数值计算最重要的基础包。大多数提供科学计算的包都是用NumPy的数组作为构建基础。 NumPy的部分功能如下…...

2024北京智源大会开幕,智源推出大模型全家桶及全栈开源技术基座新版图,大模型先锋集结共探AGI之路
2024年6月14日,第六届“北京智源大会”在中关村展示中心开幕。 北京智源大会是智源研究院主办的“AI内行顶级盛会”,以“全球视野、思想碰撞、前沿引领”为特色,汇聚海内外研究者分享研究成果、探寻前沿知识、交流实践经验。2024北京智源大会…...
)
李光明从程序员到架构师的逆袭之路(三)
我,李光明,正在参加一个重要的技术会议。会场上,我们团队正在讨论着接口设计以及接口设计模式。我深知,一个好的接口设计应当遵循简洁、清晰、可扩展的原则。比如,在设计一个用户信息查询接口时,我们会定义…...
基于Spring Boot+VUE毕业生信息招聘平台
系统详细设计 1管理员功能模块 管理员登录,管理员通过输入用户名、密码、角色等信息进行系统登录,如图1所示。 图1管理员登录界面图 管理员登录进入毕业生信息招聘平台可以查看首页、个人中心、企业管理、空中宣讲会管理、招聘岗位管理、毕业生管理、个…...

设计模式-创建型-04-建造者模式
1、盖房项目需求 1)需要建房子:这一过程为打桩、砌墙、封顶2)房子有各种各样的,比如普通房,高楼,别墅,各种房子的过程虽然一样,但是要求不要相同的3)请编写程序…...

jenkins中配置参数化,并在python脚本接收参数实现参数化执行
在公司内进行Monkey测试脚本集成jenkins时,因为需要指定公司内不同的app进行测试。那么可以有两种方法解决该问题,要么创建多个脚本文件,多个jenkins jobs,进行构建。要么可以在配置job时通过传参数的方式,在python脚本…...

【SCAU数据挖掘】数据挖掘期末总复习题库应用题及解析
1. 给定圆的半径为e ,令 MinPts3,考虑下面两幅图。 (1)哪些对象是核心对象? m,p,o,r(因为这些核心对象在半径e的范围内都至少包含MinPts3个对象) (2)哪些对象是直接密度可达的? 对象q是…...
详解)
后进先出(LIFO)详解
LIFO 是 Last In, First Out 的缩写,中文译为后进先出。这是一种数据结构的工作原则,类似于一摞盘子或一叠书本: 最后放进去的元素最先出来 -想象往筒状容器里放盘子: (1)你放进的最后一个盘子(…...

Nginx server_name 配置说明
Nginx 是一个高性能的反向代理和负载均衡服务器,其核心配置之一是 server 块中的 server_name 指令。server_name 决定了 Nginx 如何根据客户端请求的 Host 头匹配对应的虚拟主机(Virtual Host)。 1. 简介 Nginx 使用 server_name 指令来确定…...

Java-41 深入浅出 Spring - 声明式事务的支持 事务配置 XML模式 XML+注解模式
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

Robots.txt 文件
什么是robots.txt? robots.txt 是一个位于网站根目录下的文本文件(如:https://example.com/robots.txt),它用于指导网络爬虫(如搜索引擎的蜘蛛程序)如何抓取该网站的内容。这个文件遵循 Robots…...

Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决
Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决 问题背景 在一个基于 Spring Cloud Gateway WebFlux 构建的微服务项目中,新增了一个本地验证码接口 /code,使用函数式路由(RouterFunction)和 Hutool 的 Circle…...
Mobile ALOHA全身模仿学习
一、题目 Mobile ALOHA:通过低成本全身远程操作学习双手移动操作 传统模仿学习(Imitation Learning)缺点:聚焦与桌面操作,缺乏通用任务所需的移动性和灵活性 本论文优点:(1)在ALOHA…...

JVM虚拟机:内存结构、垃圾回收、性能优化
1、JVM虚拟机的简介 Java 虚拟机(Java Virtual Machine 简称:JVM)是运行所有 Java 程序的抽象计算机,是 Java 语言的运行环境,实现了 Java 程序的跨平台特性。JVM 屏蔽了与具体操作系统平台相关的信息,使得 Java 程序只需生成在 JVM 上运行的目标代码(字节码),就可以…...

保姆级教程:在无网络无显卡的Windows电脑的vscode本地部署deepseek
文章目录 1 前言2 部署流程2.1 准备工作2.2 Ollama2.2.1 使用有网络的电脑下载Ollama2.2.2 安装Ollama(有网络的电脑)2.2.3 安装Ollama(无网络的电脑)2.2.4 安装验证2.2.5 修改大模型安装位置2.2.6 下载Deepseek模型 2.3 将deepse…...

力扣热题100 k个一组反转链表题解
题目: 代码: func reverseKGroup(head *ListNode, k int) *ListNode {cur : headfor i : 0; i < k; i {if cur nil {return head}cur cur.Next}newHead : reverse(head, cur)head.Next reverseKGroup(cur, k)return newHead }func reverse(start, end *ListNode) *ListN…...

搭建DNS域名解析服务器(正向解析资源文件)
正向解析资源文件 1)准备工作 服务端及客户端都关闭安全软件 [rootlocalhost ~]# systemctl stop firewalld [rootlocalhost ~]# setenforce 0 2)服务端安装软件:bind 1.配置yum源 [rootlocalhost ~]# cat /etc/yum.repos.d/base.repo [Base…...
