FPGA - 数 - 加减乘除
一,数的表示
首先,将二进制做如下解释:
2的0次方=1
2的1次方=2
2的2次方=4
2的3次方=8
.....
以此类推,那么任何整数,或者说任意一个自然数均可以采用这种方式来表示。
例如,序列10101001,根据上述表示方法,可以很容易推算出序列所表示的数值
2的7次方 * 1 + 2的6次方 * 0 + 2的5次方 * 1+ 2的4次方 * 0 +
2的3次方 * 1 + 2的2次方 * 0 + 2的1次方 * 0 + 2的0次方 * 1 =
128 + 0 + 32 + 0 + 8 + 0 + 0 + 1 = 169
通过这个方法,整个自然数都可用0 和1这两个数字来代替。0与1这两个数字很容易被电子化:有电流就是 1,没有电流就是0。这就是整个现代计算机技术的根本秘密所在。
二,定点数
几乎所有的计算机,以及包括FPGA在内的数字信号处理器件,数字和信号变量都是用二进制数来表示的。数字使用符号0和1来表示, 称为比特(Binary Digit,bit)。其中,二进制数的小数点将数字的整数部分和小数部分分开。为了与十进制数的小数点符号相区别,使用符号∆来表示二进制数的小数点。例如,十进制数11.625的二进制 数表示为1011∆101。二进制数小数点左边的4位1011代表整数部分, 小数点右边的3位101代表数字的小数部分。对于任意一个二进制数来 讲,均可由 B 个整数位和 b 个小数位组成,即

其对应的十进制数大小(假设该二进制数为正数) D 由
![]()
给出。每一个的值取1或0。最左端的位
称为最高位(Most Significant Bit ,MSB),最右端的位
称为最低位(Least Significant Bit,LSB)
定点数有原码、反码和补码三种表示方法,这三种表示方法在 FPGA设计中使用得十分普遍
(1)原码
原码是「未经更改的码」,指一个二进制数左边加上符号位后所得到的码。
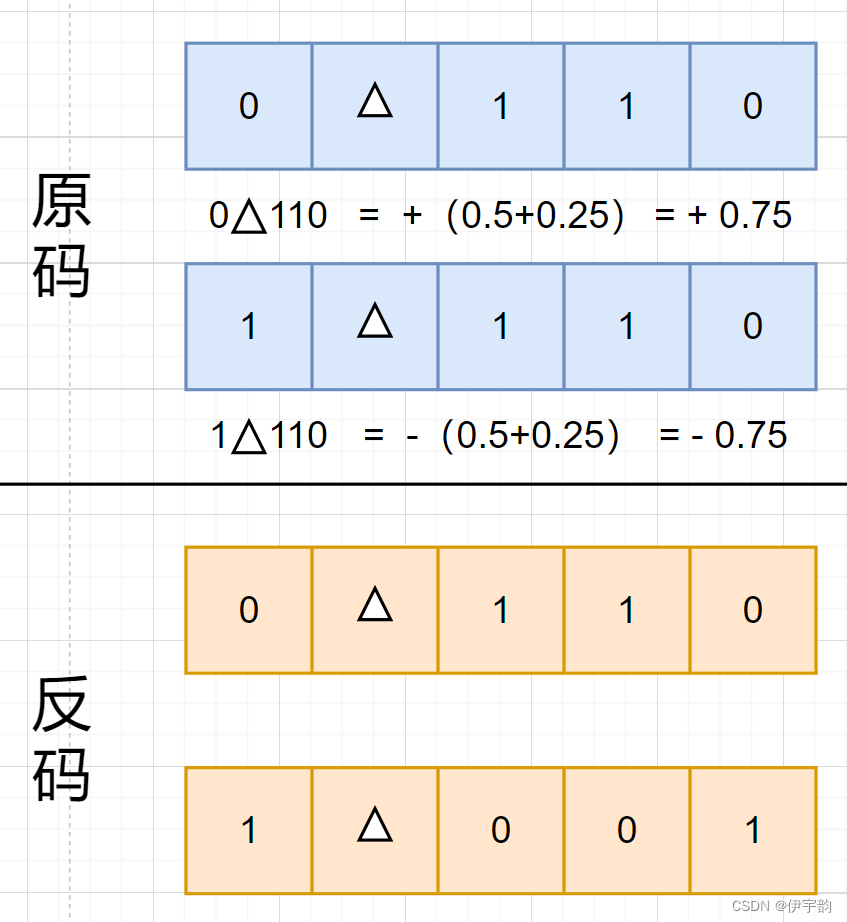
原码表示法是指符号位加绝对值的表示法。符号位通常用0表示正号,用1表示负号。例如,二进制数 ( x )2=0∆110表示+0.75,( x )2=1∆110表示-0.75。

(2)反码
正数的反码与原码相同。负数的反码为原码除了符号位的所有位 取反,即可得到负数的反码。例如,十进制数-0.75的二进制原码表示 为( x )2=1∆110,其反码为1∆001
(3)补码
正数的补码、反码及原码完全相同。
负数的补码与反码之间有一 个简单的换算关系:补码等于反码在最低位加1。
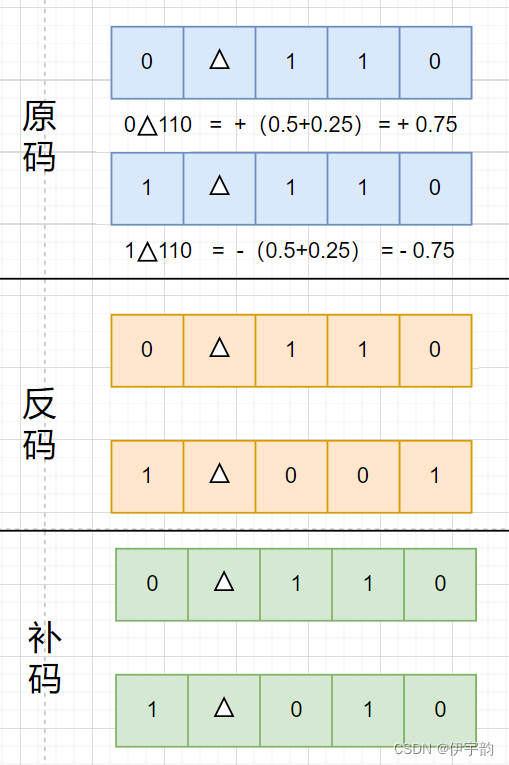
例如,十进制 数-0.75的二进制原码为1∆110,反码为1∆001,其补码为1∆010。
值得 一提的是,在二进制数的运算过程中,补码最重要的特性是减法可以用加法来实现。
原码的优点是乘除运算方便,无论正数还是负数,乘、除运算都 一样,并以符号位决定结果的正负号;若做加法则需要判断两个数符 号是否相同;若做减法,还需要判断两个数绝对值的大小,用大数减小数。
补码的优点是加法运算方便,无论正数还是负数均可直接加, 且符号位同样参与运算,如果符号位发生进位,把进位的1去掉,余下的即结果。
(4)原码与补码的运算对比
由于正数的原码和补码完全相同,因此对于加法运算来讲,原码和补码的运算方式也完全相同。补码的运算优势主要体现在减法上, 我们以一个具体的例子来分析采用补码进行减法运算的优势,在进行分析之前,先要明确的是,在电路中实现比较、加法、减法等运算 时,都需要占用相应的硬件资源,且需要耗费一定的时间。因此,完成相同的运算,所需的运算步骤越少,运算效率就越高。
假设4 bit的数 A 和 B ,其中 A 的值为6,B的值为-5,则其二进制补码分别为 A补(0110)、 B补(1011),按照二进制逢二进一的规则完成加运算,得到10001,舍去最高位1,取低4 bit的数,可得到0001,即十进制数1,结果正确。运算过程如下图:
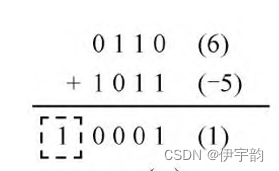
假设 A 的值为-6, B的值为5,则其二进制补码分别为 A补(1010)、 B补(0101), 按照二进制逢二进一的规则完成加运算,得到1111,(负数补码到原码的转换:除去符号位以外全部取反加1)即(0000 + 1 = 0001),即十进制数-1, 结果正确,运算过程如下图:

从上面的例子可以看出,当采用补码时,无论加法运算还是减法运算,均可通过加法运算来实现,这对电路的设计是十分方便的。
三,FPGA的加减乘除
(1)加减操作
FPGA中的二进制数可以分为定点数和浮点数两种格 式,虽然浮点数的加法和减法运算相对于定点数而言,在运算步聚和 实现难度上都要复杂得多,但浮点数的加法和减法运算仍然是通过将浮点数分解为定点数运算以及移位等步骤来实现的。
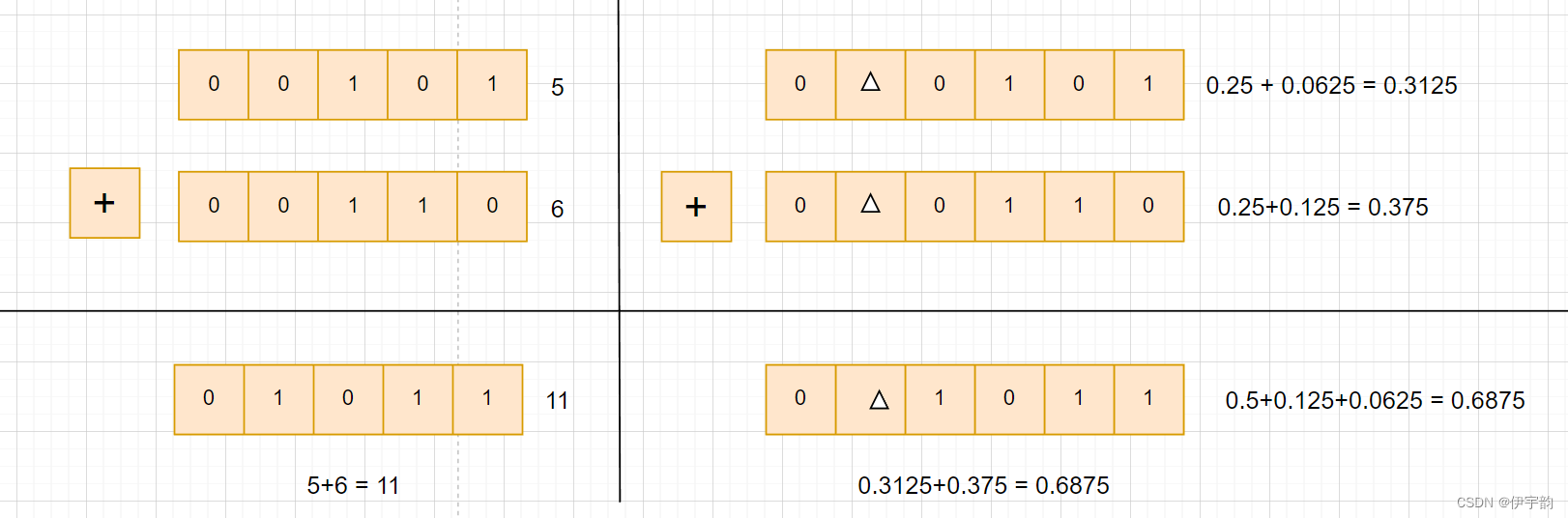
例如,对于两个二进制数00101和00110, 当进行加法运算时,Verilog HDL的编译器按二进制规则逐位相加,结果为01011。如果设计者将这两个二进制数看成无符号整数,则表示5+6=11;如果将这两个二进制数的小数点放在最高位与次高位之间, 即0∆0101和0∆0110,则表示0.3125+0.375=0.6875。
需要注意的是,与十进制数运算规则相同,在进行二进制数的加法和减法运算时,参与运算的两个二进制数的小数点位置必须对齐, 且结果的小数点位置也必须相同。
Verilog HDL如何表示负数呢?
例如,二进制数1111,在程序中是表示15还是-1?方法十分简单。
在声明端口或信号时,默认的是无符号数,如果需要将某个数指定为有符号数,则只需在声明时增加关键字signed即可。
例如,“wire signed[7:0] number;”表示将number 声明为8 bit的有符号数,在对其进行运算时自动按照有符号数来处理。
结合二进制数的运算规则可以得出以下几点结论:
- B bit的二进制数,如当成无符号整数,表示的范围为0~
;如当成有符号整数,表示的范围为
~
。
- 如果二进制数的表示范围没有溢出,将运算数据均看成无符号数或有符号数,则运算结果正确。
- 两个B bit的二进制数进行加法和减法运算,若要运算结果 不溢出,则需要 B +1 bit的数存放运算结果。
- 两个二进制数进行加法和减法运算,只要输入数据相同,不 论有符号数还是无符号数,其运算结果的二进制数就完全相同。
虽然在二进制数的加法和减法运算中,不论有符号数还是无符号数,两个二进制数的运算结果的二进制数形式完全相同,
但在Verilog HDL中,仍然有必要根据设计需要采用关键字signed对信号进行声明。 例如,在进行比较运算时,对于无符号数据,1000大于0100;对于有符号数据,1000小于0100。
在实际的工程设计中,经常会遇到多于两个操作数的加法运算 (由于补码的加法和减法运算相同,因此仅讨论加法运算)
在进行FPGA设计中还经常遇到这样一种情况,例如,有3个4 bit 的数参与加法运算,前两个数的加法结果需要用5 bit的数存储,但通过设计能保证最终的运算结果范围为-8~7,即只需用4 bit的数表示,在设计电路时,是否需要采用5 bit的数存储中间运算结果呢?
为了弄清楚这个问题,我们通过2个例子来验证一下。
例子1:
假设3个 4 bit的数进行加法运算: A =7、 B =3、 C =-4, A + B + C =6。
根据二进制数 的运算规则,首先计算 D = A + B =10,如果中间结果也采用4 bit的数表 法,则结果为-6(去掉最高位),即 D 的值为-6,再计算 D + C = E =-10, 由于结果用4 bit的数表示,去掉最高位符位号,值为6,即 E =6,结果正确。上面的运算过程如图所示

例子2:
假设3个 4 bit的数进行加法运算: A =7、 B =9、 C =-4, A + B + C =12。
根据二进制数 的运算规则,首先计算 D = A + B =16,
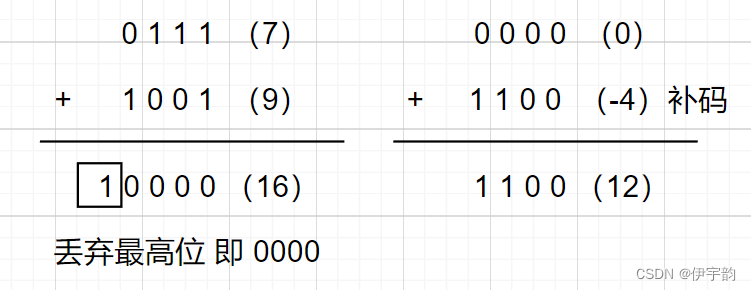
从运算结果看,如果采用补码进行运算,即使中间运算结果需要用5 bit的数表示,只要最终结果仅需用4 bit的数表示,则在实际电路设计时,中间运算结果仅用4 bit的数运算,也能最终得到正确的结果
得出结论即:当多个数进行加法运算时,如果最终的运算结果需要用 N bit 的数表示,则整个运算过程,包括中间运算结果均用 N bit的数表示, 不需考虑中间变量运算溢出的问题
(2)乘法操作
加法及减法运算在数字电路中实现相对较为简单,在采用综合工 具进行设计综合时,RTL电路图中加法和减法运算会被直接综合成加法器或减法器。乘法运算在其他软件编程语言中实现也十分简单,但用 门电路、加法器、触发器等基本逻辑单元实现乘法运算却不是一件容易的事。、
在采用Xilinx公司FPGA/CPLD进行设计时,如果选用的目标器件(如FPGA)内部集成了专用的乘法器IP核,则Verilog HDL中的乘法运算在综合成电路时将直接综合成乘法器,否则综合成由LUT等基本元件组成的乘法电路。与加法和减法运算相比,乘法器需要占用成倍的硬件资源。当然,在实际FPGA工程设计中,需要用到乘法运算时,可以尽量使用FPGA中的乘法器IP核,这种方法不仅不需要占用硬件资源,还可以达到很高的运算速度。
在FPGA设计中,乘法运算可分为信号与信号的乘法运算,以及常数与信号的乘法运算。对于信号与信号的乘法运算,通常只能使用乘法器IP核来实现;对于常数与信号的乘法运算,可以通过 移位、加法、减法运算来实现。信号 A 与常数的乘法运算如下:
A ×16= A 左移4位
A ×20= A ×16 + A ×4 = A 左移4位 + A 左移2位
A ×27= A ×32 - A ×4 - A = A 左移5位 - A 左移2位 - A
需要注意的是,由于乘法运算结果的位宽比乘数的位宽大,因此 在通过移位、加法和减法运算实现乘法运算前,需要扩展数据位宽, 以免出现数据溢出现象
(3)除法操作
在Verilog HDL编译环境中,除法、指数、求模、求余 等操作均无法在Verilog HDL中直接进行相关运算。实际上,通过基本逻辑单元构建这几种运算也是十分复杂的工作。如果要用Verilog HDL 实现这些运算,一种方法是使用提供的IP核或使用商业IP核; 另一种方法是将这几种运算分解成加法、减法、移位等运算来实现。
Xilinx的FPGA一般都提供除法器IP核。对于信号与信号的除法运算,最好的方法是采用提供的除法器IP核;对于除数是常量的除法运算,则可以采取加法、减法、移位运算来实现除法运算。下面 是一些信号 A 与常数进行除法运算。
A ÷2 ≈ A 右移1位
A ÷3 ≈ A ×(0.25+0.0625+0.0156) ≈ A 右移2位+ A 右移4位+ A 右移6位
A ÷4 ≈ A 右移2位
A ÷5 ≈ A ×(0.125+ 0.0625+0.0156) ≈ A 右移3位+ A 右移4位+ A 右移6位
需要说明的是,与普通乘法运算不同,常数乘法通过左移运算可以得到完全准确的结果,而除数是常数的除法运算却不可避免地存在 运算误差。采用分解方法的除法运算只能得到近似正确的结果,且分解运算的项数越多,精度越高。
参考:杜勇.Xilinx FPGA 数字信号处理设计[M].电子工业出版社:202003.339.
相关文章:
FPGA - 数 - 加减乘除
一,数的表示 首先,将二进制做如下解释: 2的0次方1 2的1次方2 2的2次方4 2的3次方8 ..... 以此类推,那么任何整数,或者说任意一个自然数均可以采用这种方式来表示。 例如,序列10101001,根据上述…...

软件性能测试之负载测试、压力测试详情介绍
负载测试和压力测试是软件性能测试中的两个重要概念,它们在保证软件质量和性能方面起到至关重要的作用,本文将从多个角度详细介绍这两种测试类型。 一、软件负载测试 负载测试是在特定条件下对软件系统进行长时间运行和大数据量处理的测试ÿ…...

科研辅助工具
科研工具收集 1. 如何筛选出最合适的SCI论文投稿杂志:点击直达 2. 分享三种正确查找期刊全称、缩写的网站: 点击直达...

亿达中国武汉园区入选“武汉市科技金融工作站”及“武汉市线下首贷服务站”
近日,武汉市2024科技金融早春行活动在深交所湖北资本市场培育基地举行。会上,第四批武汉市科技金融工作站试点单位名单及第五批武汉地区金融系统线下首贷服务站名单正式公布,武汉软件新城成功入选上述两个名单。 为缓解科技型企业融资难题&a…...
)
Docker配置阿里云加速器(2续)
默认情况下镜像是从docker hub下载,由于docker hub服务器在国外,由于网络原因镜像下载速度较慢,一般会配置镜像加速进行下载 国内镜像加速器有阿里云、网易云、中科大等,本章配置阿里云镜像加速器,速度较快 镜像加速源 镜像加速器 镜像加速器地址 <...

我用chatgpt写了一款程序
众所周知,Chatgpt能够帮助人们写代码,前几天苏音试着完全用Chatgpt写一款Python程序 有一句话我很赞同,未来能代替人的不是AI,是会使用AI的人。 最终,写下来效果还不错,完全提升了我的办公效率。 开发前…...
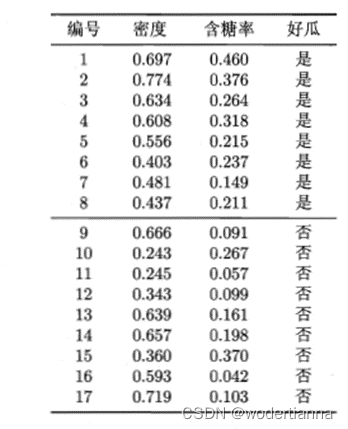
Python实现逻辑回归与判别分析--西瓜数据集
数据 数据data内容如下: 读取数据: import numpy as np import pandas as pd data pd.read_excel(D:/files/data.xlsx) 将汉字转化为01变量: label [] for i in data[好瓜]:l np.where(i 是,1,0)label.append(int(l)) data[label] lab…...
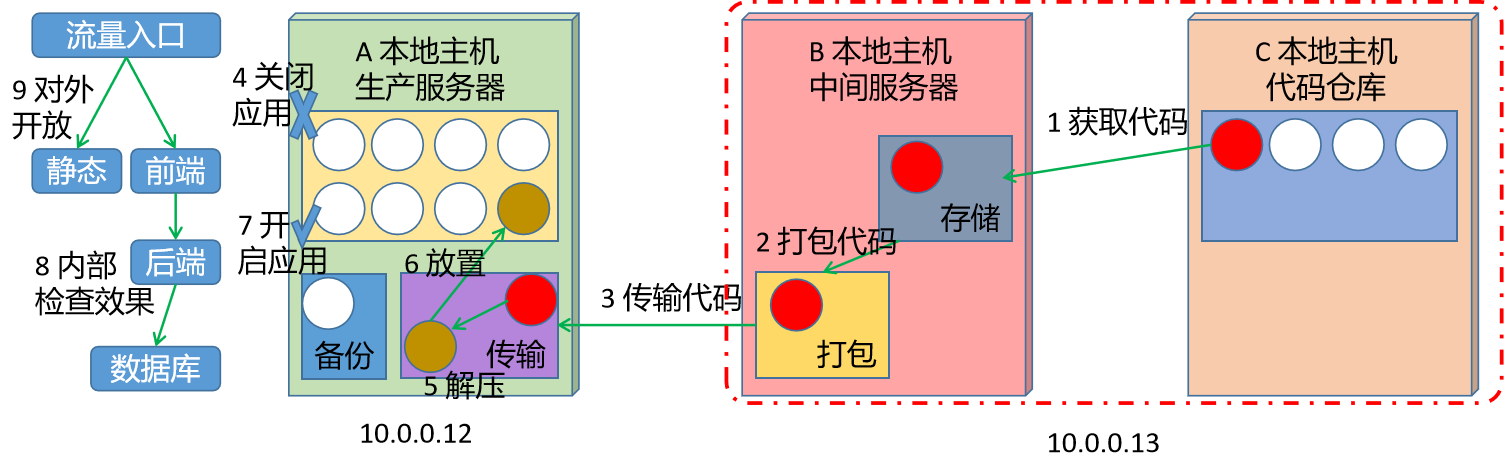
课时154:项目发布_手工发布_手工发布
1.2.3 手工发布 学习目标 这一节,我们从 基础知识、简单实践、小结 三个方面来学习 基础知识 简介 为了合理的演示生产环境的项目代码发布,同时又兼顾实际实验环境的资源,我们这里将 B主机和C主机 用一台VM主机来实现,A主机单…...
、ArkTS开发 --UI篇)
鸿蒙开发 一 (四)、ArkTS开发 --UI篇
相对布局 RelativeContainer 支持容器内部的子元素设置相对位置关系子元素支持指定兄弟元素作为锚点,也支持指定父容器作为锚点,基于锚点做相对位置布局 //alignRules 写法let AlignRus:Record<string,Record<string,string|VerticalAlign|Horiz…...

影音发烧友必入:高清先生M8 8K蓝光播放机使用体验8K播放器
影音发烧友必入:高清先生M8 8K蓝光播放机使用体验 高清先生在5.18成功举办新品8K蓝光播放机“M8”的发布会后,心心念念想尝鲜,于是果断下单了一台。 外形 收到货后,是牛皮纸包装,醒目的“高清先生”标识印在正面&…...

【34W字CISSP备考笔记】域1:安全与风险管理
1.1 理解、坚持和弘扬职业道德 1.1.1.(ISC)职业道德规范 1、行为得体、诚实、公正、负责、守法。 2、为委托人提供尽职、合格的服务。 3、促进和保护职业。 4、保护社会、公益、必需的公信和自信,保护基础设施。 1.1.2.组织道德规范 1、RFC 1087 ࿰…...

Camtasia Studio 2024软件下载附加详细安装教程
amtasia Studio 2024是一款功能强大的屏幕录制和视频编辑软件,由TechSmith公司开发。这款软件不仅能够帮助用户轻松地记录电脑屏幕上的任何操作,还可以将录制的视频进行专业的编辑和制作,最终输出高质量的视频教程、演示文稿、培训课程等。 …...
与机器学习(ML):塑造未来的技术引擎)
人工智能(AI)与机器学习(ML):塑造未来的技术引擎
目录 前言 一、人工智能(AI)概述 二、机器学习(ML)的作用:深入解析与应用前景 1、机器学习的作用机制 2、机器学习在各个领域的应用 3、机器学习的挑战与前景 三、AI与ML的融合与应用:深度解析与前景…...
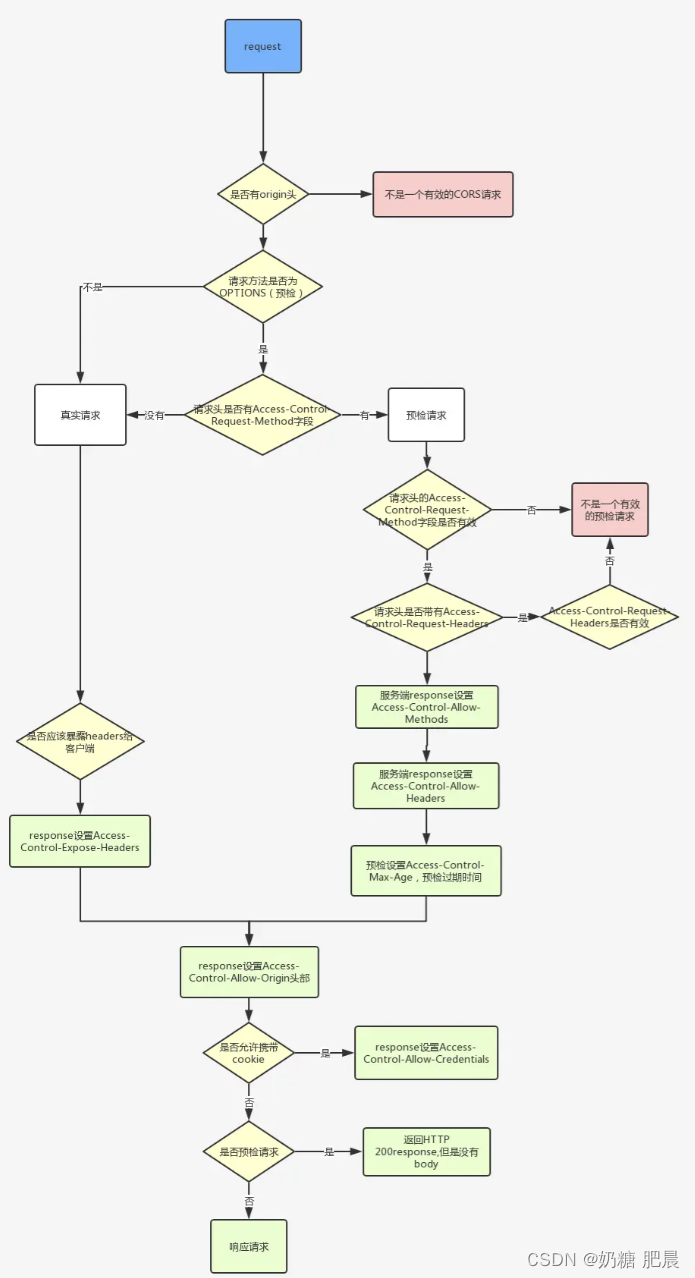
post为什么会发送两次请求详解
文章目录 导文跨域请求的预检复杂请求的定义服务器响应预检请求总结 导文 在Web开发中,开发者可能会遇到POST请求被发送了两次的情况,如下图: 尤其是在处理跨域请求时。这种现象可能让开发者感到困惑,但实际上它是浏览器安全机制…...

MySQl基础入门⑯【操作视图】完结
上一边文章内容 表准备 CREATE TABLE Students (id INT AUTO_INCREMENT PRIMARY KEY,name VARCHAR(100),email VARCHAR(255),major VARCHAR(100),score int,phone_number VARCHAR(20),entry_year INT,salary DECIMAL(10, 2) );数据准备 INSERT INTO Students (id, name, ema…...

Android Root全教程
1.安装指定镜像:https://blog.csdn.net/weixin_43846562/article/details/130028258 2.安装 magisk:https://blog.csdn.net/qq1337715208/article/details/115922514 3.打开 adb root:https://liwugang.github.io/2021/07/11/magisk_enable…...

对yoloV8进行标签过滤来实现行人检测
前言 上一章我们介绍的通过迁移学习,在新的行人数据集上使用已经学习到的特征和权重,从而更快地实现行人检测任务。模型就会调整其参数以适应新的数据集,以提高对行人的识别性能。接下来介绍一种更快更便捷的方法,依旧是基于yolo…...

论文阅读笔记:Towards Higher Ranks via Adversarial Weight Pruning
论文阅读笔记:Towards Higher Ranks via Adversarial Weight Pruning 1 背景2 创新点3 方法4 模块4.1 问题表述4.2 分析高稀疏度下的权重剪枝4.3 通过SVD进行低秩逼近4.4 保持秩的对抗优化4.5 渐进式剪枝框架 5 效果5.1 和SOTA方法对比5.2 消融实验5.3 开销分析 6 结…...

目前常用的后端技术
在后端开发中,有多种技术和框架可供选择,具体取决于项目的需求、团队的技能和经验,以及组织的架构决策。以下是一些常见的后端开发技术和框架: 1. 编程语言 Java: 广泛使用于企业级应用,有大量的库和框架…...
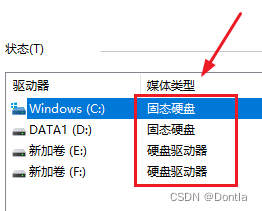
windows如何查看硬盘类型(查看磁盘类型)(查看是固态硬盘ssd还是机械硬盘hdd)(Windows优化驱动器——媒体类型)
文章目录 方法:使用Windows优化驱动器1、在任务栏搜索框中输入“优化驱动器”并打开它。2、在优化驱动器的窗口中,查看每个驱动器旁边的“媒体类型”。3、如果列出的是“固态驱动器”,那么它是SSD;如果是“硬盘驱动器”࿰…...

盘古信息PCB行业解决方案:以全域场景重构,激活智造新未来
一、破局:PCB行业的时代之问 在数字经济蓬勃发展的浪潮中,PCB(印制电路板)作为 “电子产品之母”,其重要性愈发凸显。随着 5G、人工智能等新兴技术的加速渗透,PCB行业面临着前所未有的挑战与机遇。产品迭代…...

线程同步:确保多线程程序的安全与高效!
全文目录: 开篇语前序前言第一部分:线程同步的概念与问题1.1 线程同步的概念1.2 线程同步的问题1.3 线程同步的解决方案 第二部分:synchronized关键字的使用2.1 使用 synchronized修饰方法2.2 使用 synchronized修饰代码块 第三部分ÿ…...

【git】把本地更改提交远程新分支feature_g
创建并切换新分支 git checkout -b feature_g 添加并提交更改 git add . git commit -m “实现图片上传功能” 推送到远程 git push -u origin feature_g...
)
【RockeMQ】第2节|RocketMQ快速实战以及核⼼概念详解(二)
升级Dledger高可用集群 一、主从架构的不足与Dledger的定位 主从架构缺陷 数据备份依赖Slave节点,但无自动故障转移能力,Master宕机后需人工切换,期间消息可能无法读取。Slave仅存储数据,无法主动升级为Master响应请求ÿ…...
)
是否存在路径(FIFOBB算法)
题目描述 一个具有 n 个顶点e条边的无向图,该图顶点的编号依次为0到n-1且不存在顶点与自身相连的边。请使用FIFOBB算法编写程序,确定是否存在从顶点 source到顶点 destination的路径。 输入 第一行两个整数,分别表示n 和 e 的值(1…...

AI,如何重构理解、匹配与决策?
AI 时代,我们如何理解消费? 作者|王彬 封面|Unplash 人们通过信息理解世界。 曾几何时,PC 与移动互联网重塑了人们的购物路径:信息变得唾手可得,商品决策变得高度依赖内容。 但 AI 时代的来…...

RSS 2025|从说明书学习复杂机器人操作任务:NUS邵林团队提出全新机器人装配技能学习框架Manual2Skill
视觉语言模型(Vision-Language Models, VLMs),为真实环境中的机器人操作任务提供了极具潜力的解决方案。 尽管 VLMs 取得了显著进展,机器人仍难以胜任复杂的长时程任务(如家具装配),主要受限于人…...

计算机基础知识解析:从应用到架构的全面拆解
目录 前言 1、 计算机的应用领域:无处不在的数字助手 2、 计算机的进化史:从算盘到量子计算 3、计算机的分类:不止 “台式机和笔记本” 4、计算机的组件:硬件与软件的协同 4.1 硬件:五大核心部件 4.2 软件&#…...

MinIO Docker 部署:仅开放一个端口
MinIO Docker 部署:仅开放一个端口 在实际的服务器部署中,出于安全和管理的考虑,我们可能只能开放一个端口。MinIO 是一个高性能的对象存储服务,支持 Docker 部署,但默认情况下它需要两个端口:一个是 API 端口(用于存储和访问数据),另一个是控制台端口(用于管理界面…...

Kubernetes 网络模型深度解析:Pod IP 与 Service 的负载均衡机制,Service到底是什么?
Pod IP 的本质与特性 Pod IP 的定位 纯端点地址:Pod IP 是分配给 Pod 网络命名空间的真实 IP 地址(如 10.244.1.2)无特殊名称:在 Kubernetes 中,它通常被称为 “Pod IP” 或 “容器 IP”生命周期:与 Pod …...
