FPGA - 滤波器 - IIR滤波器设计
一,IIR滤波器
在FPGA - 滤波器 - FIR滤波器设计中可知,数字滤波器是一个时域离散系统。任何一个时域离散系统都可以用一个N阶差分方程来表示,即:
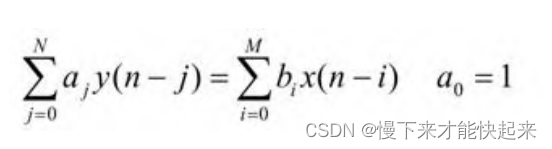
式中,x(n)和y(n)分别是系统的输入序列和输出序列;aj和bi均为常数;y(n-j)和x(n-i)项只有一次幂,没有相互交叉相乘项,故称为线性常系数差分方程。差分方程的阶数是由方程y(n-j)项中j的最大值与 最小值之差确定的。式中,y(n-j)项j的最大值取N,最小值取 0,因此称为N阶差分方程。
当aj=0且j>0时,N阶差分方程表示的系统为FIR滤波器。当aj≠0 且 j>0 时 ,N阶差分方程表 示的系统为IIR( Infinite Impulse Response)滤波器。
IIR滤波器的单位脉冲响应是无限长的,其系统函数为:

系统的差分方程可以写成:
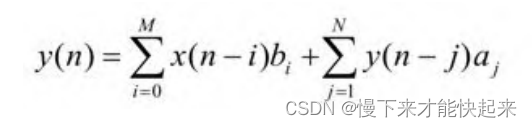
从系统的差分方程可以很容易看出,IIR滤波器有以下几个显著特性。
- IIR滤波器同时存在不为零的极点和零点,要保证IIR滤波器是稳定的系统,需要使系统的极点在单位圆内。也就是说,系统的稳定性是由系统的极点决定的。
- 由于线性相位滤波器所有的零点和极点都是关于单位圆对称的,所以只允许极点位于单位圆的原点。由于IIR滤波器存在不为零的极点,因此只可能实现近似的线性相位特性。也正是因为IIR滤波器的非线性相位特性限制了其应用范围。
- 在FPGA等数字硬件平台上实现IIR滤波器时,由于存在反馈结构,因此受限于寄存器的长度,无法通过增加字长来实现全精度的运算,运算过程中的有限字长效应是实现IIR滤波器时必须考虑的问题。
二,FIR滤波器和IIR滤波器比较
IIR滤波器与FIR滤波器是最常见的数字滤波器,两者的结构及分析方法相似。为了更好地理解这两种数字滤波器的异同,下面对它们进行简单的比较:
- 在满足相同幅频响应设计指标的情况下,FIR滤波器的阶数通常是IIR滤波器的阶数的5~10倍。
- FIR滤波器能得到严格的线性相位特性(当FIR滤波器系数具 有对称结构时)。在相同的阶数情况下,IIR滤波器具有更好的幅度特性,但相位特性是非线性的。
- FIR滤波器的单位脉冲响应是有限长的,一般采用非递归结构,必定是稳定的系统,即使在有限精度运算时,误差也比较小,受有限字长效应的影响较小。IIR滤波器必须采用递归结构,只有极点在单位圆内时才是稳定的系统;IIR滤波器具有反馈结构,由于运算过程中的截位处理,容易引起振荡现象。
- FIR滤波器的运算是一种卷积运算,可以采用快速傅里叶变换和其他快速算法,运算速度快。IIR滤波器无法采用类似的快速算法。
- 在设计方法上,IIR滤波器可以利用模拟滤波器的设计公式、数据和表格等资料。FIR滤波器不能借助模拟滤波器的设计成果。 由于计算机设计软件的发展,在设计FIR滤波器和IIR滤波器时均可采用现成的函数,因此在工程设计中两者的设计难度均已大幅下降。
- IIR滤波器主要用于设计规格化的、频率特性为分段恒定的标准滤波器,FIR滤波器要灵活得多,适应性更强。
- 在FPGA设计中,FIR滤波器可以采用现成的IP核进行设计, 工作量较小;用于IIR滤波器设计的IP核很少,一般需要手动编写代码,工作量较大。
- 当给定幅频响应,而不考虑相位特性时,如果FPGA的逻辑资源较少,则可采用IIR滤波器;当要求滤波器具有严格线性相位特性, 或幅度特性不同于典型模拟滤波器的特性时,通常采用FIR滤波器
三,IIR滤波器的MATLAB设计
一般来讲,IIR滤波器的设计方法可以分为三种:原型转换法、直接设计法,以及直接调用MATLAB中设计IIR滤波器的函数。从工程设计 的角度来讲,前两种设计方法都比较烦琐,且需要对IIR滤波器的基础 理论知识有更多的了解,因此工程中大多直接调用MATLAB中设计IIR滤波器的函数。
MATLAB提供了多种用于设计IIR滤波器的函数,通常采用的是根据 原型转换法实现的5种设计IIR滤波器的函数:butter()函数(巴特沃斯函数)、cheby1()函数(切比雪夫I型函数)、cheby2()函数(切比雪夫Ⅱ型函数)、ellip()函数(椭圆滤波器函数)及yulewalk()函数。
3.1 butter()函数设计IIR滤波器
在MATLAB中,可以利用butter()函数直接设计各种形式的数字滤 波器(也可设计模拟滤波器),其语法为:
[b,a] = butter(n,Wn);
[b,a] = butter(n,Wn,'ftype');
[z,p,k] = butter(n,Wn);
[z,p,k] = butter(n,Wn,'ftype');
[A,B,C,D] = butter(n,Wn);
[A,B,C,D] = butter(n,Wn,'ftype');butter()函数可以设计低通、高通、带通和带阻等各种形式的滤波器。
输入参数 :
n - 滤波器阶数 整数标量
Wn - 截止频率,注意:Wn = fc_low/(fs/2) 标量 | 二元素向量
ftype - 滤波器类型 'low' | 'bandpass' | 'high' | 'stop'输出参数:
b,a - 传递函数系数 行向量
z,p,k - 零点、极点和增益 列向量、标量
A,B,C,D - 状态空间矩阵 矩阵
例如,要设计采样频率为2000 Hz、阶数为12、截止频率为600 Hz 的高通巴特沃斯数字滤波器,并画出滤波器的频率响应,只需在 MATLAB中使用下面的命令即可。
[b,a] = butter(12,600*2/2000,'high');
freqz(b,a,128,2000);3.2 cheby1()函数设计IIR滤波器
在MATLAB中,可以利用cheby1()函数直接设计各种形式的数字滤 波器(也可设计模拟滤波器),其语法为:
[b,a] = cheby1(n,Rp,Wn);
[b,a] = cheby1(n,Rp,Wn,'ftype');
[z,p,k] = cheby1(n,Rp,Wn);
[z,p,k] = cheby1(n,Rp,Wn,'ftype');
[A,B,C,D] = cheby1(n,Rp,Wn);
[A,B,C,D] = cheby1(n,Rp,Wn,'ftype');cheby1函数先设计出切比雪夫I型的模拟原型滤波器,然后用原型变换法得到数字低通、高通、带通或带阻滤波器。切比雪夫I型滤波器 在通带是等纹波的,在阻带是单调的,可以设计低通、高通、带通和 带阻各种形式的滤波器。
输入参数 :
n - 滤波器阶数 整数标量Rp -通带纹波最大衰减 单位(dB)
Wn - 截止频率,注意:Wn = fc_low/(fs/2) 标量 | 二元素向量
ftype - 滤波器类型 'low' | 'bandpass' | 'high' | 'stop'输出参数:
b,a - 传递函数系数 行向量
z,p,k - 零点、极点和增益 列向量、标量
A,B,C,D - 状态空间矩阵 矩阵
例如,要设计采样频率为2000 Hz、阶数为12、截止频率为600 Hz、通带衰减为0.5 dB的低通切比雪夫I型数字滤波器,并画出滤波器的频率响应,只需在MATLAB中使用以下命令即可。
[b,a] = cheby1(12,0.5,600*2/2000);
freqz(b,a,128,2000);3.3 cheby2()函数设计IIR滤波器
用cheby2()函数直接设计各种形式的数字滤波器(也可设计模拟滤波器)。
函数的使用方法与cheby1()完全相同,只是利用cheby1()函数设计的滤波器在通带是等纹波的,在阻带是单调的;而利用cheby2()函数设计的滤波器在阻带是等纹波的,在通带是单调的。
例如,要设计采样频率为2000 Hz、阶数为12、截止频率为600 Hz、通带衰减为0.5 dB的低通切比雪夫II型数字滤波器,并画出滤波器的频率响应,只需在MATLAB中使用以下命令即可。
[b,a] = cheby2(12,0.5,600*2/2000);
freqz(b,a,128,2000);3.4 ellip()函数设计IIR滤波器
在MATLAB中,可以利用ellip()函数直接设计各种形式的数字滤波 器(也可设计模拟滤波器),其语法为:
[b,a] = ellip(n,Rp,Rs,Wn);
[b,a] = ellip(n,Rp,Rs,Wn,'ftype');
[z,p,k] = ellip(n,Rp,Rs,Wn);
[z,p,k] = ellip(n,Rp,Rs,Wn,'ftype');
[A,B,C,D] = ellip(n,Rp,Rs,Wn);
[A,B,C,D] = ellip(n,Rp,Rs,Wn,'ftype');在利用ellip()函数设计IIR滤波器时,先设计出椭圆滤波器,然后用原型变换法得到数字低通、高通、带通或带阻滤波器。在模拟滤波器的设计中,采用椭圆滤波器的设计是最为复杂的一种设计方法, 但它设计出的滤波器的阶数最小,同时它对参数的量化灵敏度最敏感。
输入参数 :
n - 滤波器阶数 整数标量Rp -通带纹波最大衰减 单位(dB)
Rs -阻带波纹最小衰减 单位 (dB)
Wn - 截止频率,注意:Wn = fc_low/(fs/2) 标量 | 二元素向量
ftype - 滤波器类型 'low' | 'bandpass' | 'high' | 'stop'输出参数:
b,a - 传递函数系数 行向量
z,p,k - 零点、极点和增益 列向量、标量
A,B,C,D - 状态空间矩阵 矩阵
例如,要设计采样频率为2000 Hz、阶数为12、截止频率为600 Hz、通带衰减为5dB、阻带衰减为80 dB的低通椭圆滤波器,并画出滤波器的频率响应,只需在MATLAB中使用以下命令即可。
[b,a] = ellip(12,5,8,0,600*2/2000);
freqz(b,a,128,2000);3.5 yulewalk()函数设计IIR滤波器
在MATLAB中,yulewalk()函数用于设计递归数字滤波器。与前面介绍的几种IIR滤波器设计函数不同的是,yulewalk()函数只能设计数字滤波器,不能设计模拟滤波器。yulewalk()实际是一种在频域采用 了最小均方法来设计滤波器的函数,其语法形式为:
[b,a] = yulewalk(n,f,m)
yulewalk()函数中的参数n表示滤波器的阶数,f 和m用于表征滤波器的幅频响应。其中f是一个向量,它的每一个元素都是0~1的实数, 表示频率,其中1表示采样频率的1/2,且f中的元素必须是递增的,第 一个元素必须是0,最后一个元素必须是1。m是频率f处的幅度响应, 它也是一个向量,长度与f相同。当确定了理想滤波器的频率响应后, 为了避免从通带到阻带的过渡陡峭,应对过渡带宽进行多次仿真试验,以便得到最优的滤波器设计。
例如,要设计一个12阶的低通滤波器,滤波器的截止频率为600 Hz,采样频率为2000 Hz,采用yulewalk()函数的设计方法为:
f = [0 600*2/2000 600*2/2000 1];
m = [1 1 0 0];
[b,a] = yulewalk(9,f,m);
freqz(b,a,128,2000);
3.6 使用FDATOOL设计IIR滤波器
除了一些常用的滤波器函数,MATLAB还提供了数字滤波器的专用 设计工具FDATOOL。FDATOOL的突出优点是直观、方便,用户只需设置几个参数,即可查看IIR滤波器频率响应、零点/极点、单位脉冲响应、系数等信息。
例子:采用FDATOOL设计带通IIR滤波器
采用FDATOOL设计一个带通IIR滤波器,通带范围为1200~2400 Hz,低频过渡带宽为900~1200 Hz,高频过渡带宽为2400~2700 Hz, 采样频率为9000 Hz的等阻带纹波滤波器,要求阻带衰减大于70 dB。
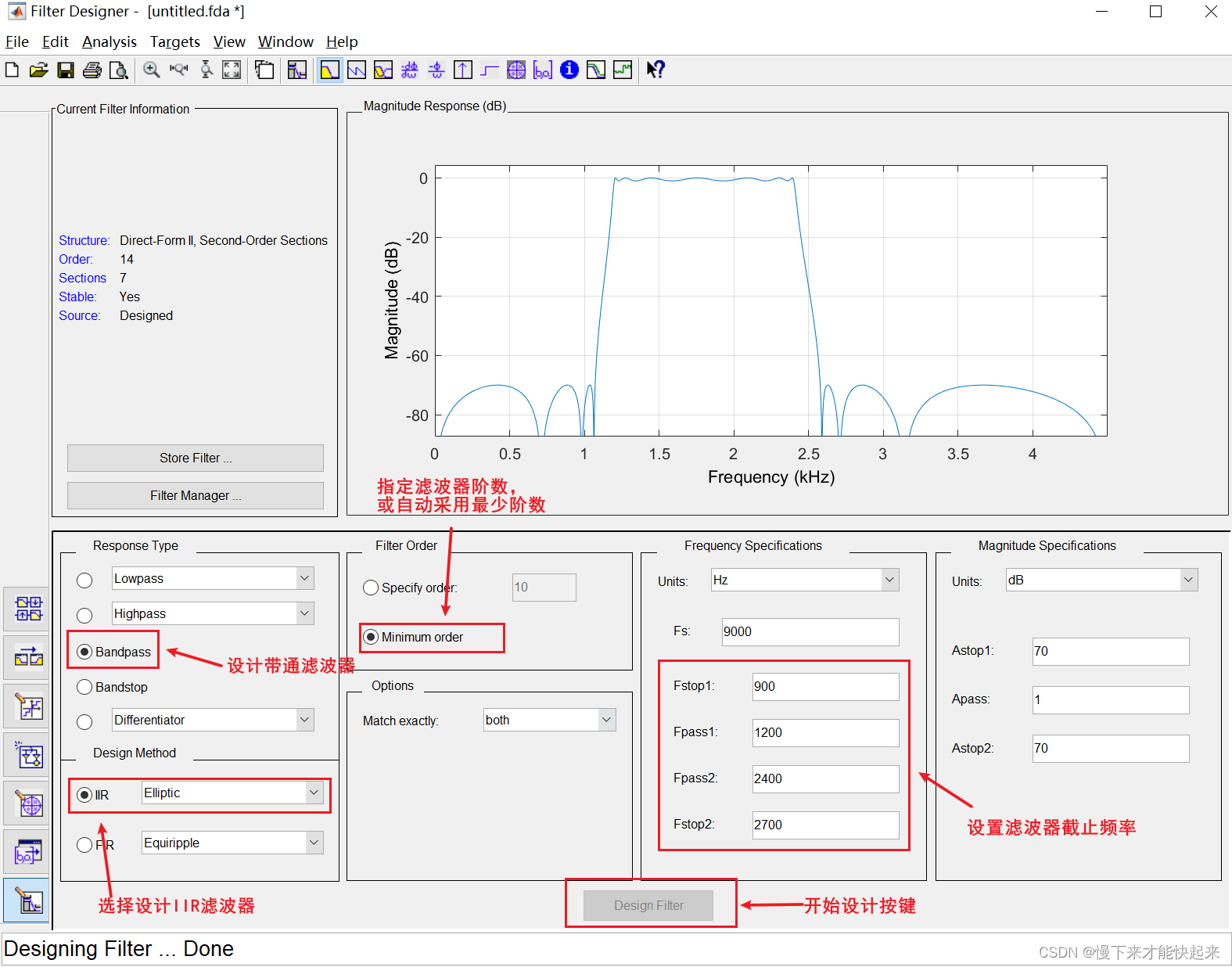
启动MATLAB后,在命令行窗口中输入“fdatool”后按下回车键, 即可打开FDATOOL界面,如上图所示。
- 第一步:在“Frequency Specifications”中设置IIR滤波器的 截止频率。
- 第二步:在“Response Type”中选中“Bandpass”,表示设计的是带通IIR滤波器。
- 第三步:在“Design Method”中选中“IIR”,在“IIR”的下 拉列表中选择“Elliptic”。
- 第四步:在“Filter Order”中选中“Minimum order”,表示 采用最小阶数来完成设计。
- 第 五 步 : 单 击 FDATOOL 界 面 左 下 方 的 “ ” 按 钮 ( Design Filter,滤波器设计)即可开始IIR滤波器的设计。
- 第六步:根据FDATOOL中的幅频响应曲线调整IIR滤波器的阶数, 直到满足设计要求为止。
- 至此,使用FDATOOL完成了带通滤波器的设计,用户可以通过 单击菜单“Analysis→ Filter Coefficients”来查看IIR滤波器的系数。
四,IIR滤波器的FPGA实现
4.1 IIR滤波器系数的量化方法
例如,采用 cheby2()函数设计一个阶数为7(长度为8)、采样频率为12.5MHz、截 止频率为3.125MHz、阻带衰减为60 dB的低通IIR滤波器,可在MATLAB 的命令行窗口中直接输入下面的命令:
[b,a] = cheby2(7,60,0.5);按回车键后,可以直接在命令行窗口中获取低通IIR滤波器的系数 向量,即:

在进行FPGA实现时,必须对低通IIR滤波器的系数进行量化处理, 如对系数进行12 bit量化,可在MATLAB命令行窗口中直接输入下面的 命令:
m = max(max(abs(a),abs(b)));
Qb = round(b/m*(2^(12-1)-1));
Qa = round(a/m*(2^(12-1)-1));即:

Qb = [13 38 74 99 99 74 38 13]
Qa = [900 -1632 2047 -1427 725 -215 42 -3]根据低通IIR滤波器系统函数,可直接写出其差分方程,即:
900y(n)=13[x(n)+x(n-7)]+38[x(n-1)+x(n-6)]+74[x(n-2)+x(n-5)]+99[x(n-3)+x(n-4)]-[-1623y(n-1)+2047y(n-2)-1427y(n-3)+725y(n-4)-215y(n-5)+42y(n-6)-3y(n-7)]需要特别注意的是,上式的左边乘了一个常系数,即量化后 的Qa(1)。由于上式的递归特性,为了正确求解下一个输出值, 需要在计算上式右边后除以900,以获取正确的输出结果。也就是说,在FPGA实现时需要增加一级常数除法运算。
在进行除法运算的FPGA实现时,即使常系数的除法运算,也是十分耗费资源的。但当除数是2的整数幂次方时,可根据二进制数运算的特点,直接采用移位的方法来近似实现除法运算。移位运算不仅占用 的硬件资源少,而且运算速度快。因此,在上式所表示的低通IIR滤波器时,一个简单可行的方法是在进行系数量化时,有意将量化后的分母项系数的第一项设置为2的整数幂次方。仍然采用MATLAB来 对低通IIR滤波器系数进行量化,其命令为:
m = max(max(abs(a),abs(b)));
Qm = floor(log2(m/a(1)));
if Qm < log2(m/a(1))Qm = Qm + 1;
end
Qm = 2^Qm;
Qb = round(b/Qm*(2^(12-1)-1));
Qa = round(a/Qm*(2^(12-1)-1));
disp(Qb);
disp(Qa);即:

Qb = [ 7 21 42 56 56 42 21 7]
Qa = [512 -922 1163 -811 412 -122 24 -2]4.2 IIR滤波器的FPGA设计
对上述例子所述的IIR滤波器进行Verilog HDL设计,并仿真测试 FPGA实现后的IIR滤波效果,其中系统时钟信号频率为12.5 MHz、数据输入速率为12.5 MHz、输入数据的位宽为8,对IIR滤波器的系数进行12 bit量化。
所要实现的IIR滤波器的差分方程为:
512y(n)=7[x(n)+x(n-7)]+21[x(n-1)+x(n-6)]+42[x(n-2)+x(n-5)]+56[x(n-3)+x(n-4)]-[-922y(n-1)+1163y(n-2)-811y(n-3)+412y(n-4)-122y(n-5)+24y(n-6)-2y(n-7)] 计算上式右边后,再除以512即可完成一次完整的滤波运 算。根据FPGA的特点,可采用右移9 bit的方法来近似实现除以512运算。因此,直接型结构IIR滤波器的实现结构如图表示。

从上图可以看出,对于零点处(零点系数)直接型结构IIR滤波器实现结构,其实可完全看成没有反馈结构的FIR滤波器,并且可以利用对称系数的特点进一步减少乘法运算。对于极点处(极点系数)直接型结构IIR滤波器的实现结构,即求取Yout信号的过程,也可以看成 一个没有反馈结构的FIR滤波器。整个IIR滤波器的闭环过程是在求取 Ysum的减法器,以及移位算法实现除法运算的过程中完成的。
4.2.1 零点系数的Verilog 代码设计
零点处的IIR滤波器可完全看成FIR滤波器,因此可采用FIR滤波器 的FPGA实现方法。
代码如下:
module zero_point(input clk ,input reset ,input signed [7 :0] Xin ,output signed [15:0] Xout ); reg signed [7:0]Xin_reg [7:0];reg [3:0] i;reg [3:0] j;//数据存入到移位寄存器always @(posedge clk or negedge reset) begin if(reset) beginfor(i=0;i<8;i=i+1)Xin_reg[i] <= 8'd0;end else beginfor(j=0;j<8;j=j+1)Xin_reg[j+1] <= Xin_reg[j];Xin_reg[0] <= Xin;endend//对称系数的输入数据相加wire signed [8:0] Add_reg[3:0];assign Add_reg[0] = Xin_reg[0] + Xin_reg[7];assign Add_reg[1] = Xin_reg[1] + Xin_reg[6];assign Add_reg[2] = Xin_reg[2] + Xin_reg[5];assign Add_reg[3] = Xin_reg[3] + Xin_reg[4];//采用移位(左移)相加方法实现乘法运算wire [15:0] Mult_reg[3:0];assign Mult_reg[0] = {{6{Add_reg[0][8]}},Add_reg[0],2'd0} + {{7{Add_reg[0][8]}},Add_reg[0],1'd0} + {{8{Add_reg[0][8]}},Add_reg[0]}; //7 = 2^2 + 2^1 + 2^0assign Mult_reg[1] = {{4{Add_reg[1][8]}},Add_reg[1],4'd0} + {{6{Add_reg[1][8]}},Add_reg[1],2'd0} + {{8{Add_reg[1][8]}},Add_reg[1]}; //12 = 2^4 + 2^2 + 2^0assign Mult_reg[2] = {{3{Add_reg[2][8]}},Add_reg[2],5'd0} + {{5{Add_reg[2][8]}},Add_reg[2],3'd0} + {{7{Add_reg[2][8]}},Add_reg[2],1'd0}; //42 = 2^5 + 2^3 + 2^1assign Mult_reg[3] = {{3{Add_reg[3][8]}},Add_reg[3],5'd0} + {{4{Add_reg[3][8]}},Add_reg[3],4'd0} + {{5{Add_reg[3][8]}},Add_reg[3],3'd0}; //56 = 2^5 + 2^4 + 2^3//对IIR滤波器系数与输入数据的相乘结果进行累加,assign Xout = Mult_reg[0] + Mult_reg[1] + Mult_reg[2] + Mult_reg[3];
endmodule4.2.2 极点系数的Verilog 代码设计
极点处的IIR滤波器也可可完全看成一个FIR滤波器,因此可采用 FIR滤波器的FPGA实现方法。
![]()
其中:
Zero(n) = 7[x(n)+x(n-7)]+21[x(n-1)+x(n-6)]+42[x(n-2)+x(n-5)]+56[x(n-3)+x(n-4)]
Pole(n) = [-922y(n-1)+1163y(n-2)-811y(n-3)+412y(n-4)-122y(n-5)+24y(n-6)-2y(n-7)]
y(n) = [zero(n)-Pole(n)]/512 (8-14)由于极点系数绝对值的和为3456(922+1163+811+412+122+24+2)(不包括y(n)前面的系数512), 因此输出数据相对于输入数据需增加12 bit,共20 bit。
代码如下:
module pole_point (input clk ,input reset ,input signed [7 :0] Yin ,output signed [15:0] Yout
);reg signed [7:0]Yin_reg[6:0];reg [3:0] i;reg [3:0] j;//将数据存入到以为寄存器Yin_reg中always @(posedge clk or negedge reset) begin if(reset) beginfor(i=0;i<7;i=i+1)Yin_reg[i] <= 8'd0;end else beginfor(j=0;j<7;j=j+1)Yin_reg[j+1] <= Yin_reg[j];Yin_reg[0 ] <= Yin;endend//实例化有符号乘法器IP核wire signed [11:0] coe [7:0];wire signed [19:0] Mult_reg[6:0];// assign coe[0] = 12'd512;assign coe[1] = 12'd922;assign coe[2] = 12'd1163;assign coe[3] = 12'd811;assign coe[4] = 12'd412;assign coe[5] = 12'd122;assign coe[6] = 12'd24;assign coe[7] = 12'd2;mult u1(.a(coe[1]), .b(Yin_reg[0]), .p(Mult_reg[0]));mult u2(.a(coe[2]), .b(Yin_reg[1]), .p(Mult_reg[1]));mult u3(.a(coe[3]), .b(Yin_reg[2]), .p(Mult_reg[2]));mult u4(.a(coe[4]), .b(Yin_reg[3]), .p(Mult_reg[3]));mult u5(.a(coe[5]), .b(Yin_reg[4]), .p(Mult_reg[4]));mult u6(.a(coe[6]), .b(Yin_reg[5]), .p(Mult_reg[5]));mult u7(.a(coe[7]), .b(Yin_reg[6]), .p(Mult_reg[6]));//对IIR滤波器系数和输入数据相乘结果累加assign Yout = Mult_reg[0] + Mult_reg[1] + Mult_reg[2] + Mult_reg[3] +Mult_reg[4] + Mult_reg[5] + Mult_reg[6];endmodule4.2.3 顶层文件的代码设计
顶层文件代码:
module IIR_filter (input clk ,input reset ,input signed [7 :0] din ,output signed [15:0] dout
);//例化 零点 极点模块wire [15:0]Xout;wire signed [7: 0]Yin;wire signed [19:0]Yout;wire signed [20:0]Ysum;zero_point zero_point_inst(.clk (clk) ,.reset (reset) ,.Xin (din) ,.Xout (Xout)); pole_point pole_point_inst(.clk (clk) ,.reset (reset) ,.Yin (Yin) ,.Yout (Yout) );assign Ysum = Xout - Yout;//IIR滤波器系数中的a(1) = 512,需要将加法结果除以512,可采用右移9位方法实现wire signed [20:0] Ydiv;assign Ydiv = {{9{Ysum[20]}},Ysum[20:9]};//IIR滤波器输出数据范围与输入数据范围相同assign Yin = (reset) ? 8'd0 : Ydiv[7:0];assign dout = Yin;endmoduleIIR滤波器输出数据为Ysum除以512的结果。为 了减少运算资源、提高运算速度,可采用右移9位的方法来实现近似除以512的运算。由于IIR滤波器的输出数据的位宽与输入数据的位宽相 同,因此直接取Ydiv的低8bit作为IIR滤波器的最终输出数据。
参考文献:
[1]刘谋,张梦豪,余丽仙,等.基于FPGA的IIR数字滤波器设计方法[J].电子技术,2020,49(11):1-3.
[2]杜勇.Xilinx FPGA 数字信号处理设计[M].电子工业出版社:202003.339.
[3]黄玉健,黄永庆.基于Matlab的级联型IIR滤波器设计与FPGA实现[J].梧州学院学报,2018,28(06):26-32.
[4]陈鑫磊,辛晓宁,黄鑫.IIR数字滤波器设计与FPGA实现[J].微处理机,2018,39(01):43-47.
[5]李秀花,马雯.基于FPGA的IIR数字滤波器设计与实现[J].电子技术,2016,45(05):58-60.
相关文章:

FPGA - 滤波器 - IIR滤波器设计
一,IIR滤波器 在FPGA - 滤波器 - FIR滤波器设计中可知,数字滤波器是一个时域离散系统。任何一个时域离散系统都可以用一个N阶差分方程来表示,即: 式中,x(n)和y(n)分别是系统的输入序列和输出序列;aj和bi均为…...
练习时长 1 年 2 个月的 Java 菜鸡练习生最近面经,期望25K
面经哥只做互联网社招面试经历分享,关注我,每日推送精选面经,面试前,先找面经哥 自我介绍:本人是练习时长 1 年 2 个月的 Java 后端菜鸡练习生。下面是我最近面试的面经: 百度 一面 约1h时间:2…...
计算机跨考现状,两极分化现象很严重
其实我觉得跨考计算机对于一些本科学过高数的同学来说有天然的优势 只要高数能学会,那计算机那几本专业课,也能很轻松的拿下,而对于本科是文科类的专业,如果想跨考计算机,难度就不是一般的大了。 现在跨考计算机呈现…...
leetcode73 矩阵置零
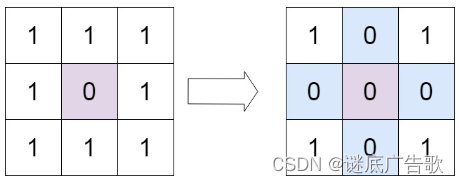
题目 给定一个 m x n 的矩阵,如果一个元素为 0 ,则将其所在行和列的所有元素都设为 0 。请使用 原地 算法。 示例 输入:matrix [[1,1,1],[1,0,1],[1,1,1]] 输出:[[1,0,1],[0,0,0],[1,0,1]] 解析 这道题题目上要求用原地算法…...

了解 XML HttpRequest 及其在 Web 开发中的应用
XML HttpRequest(XHR) 技术是构建动态、响应式网站的关键。这项技术使得网页能在不重新加载整个页面的情况下与服务器进行数据交互,极大地优化了用户的交互体验。 定义 XML HttpRequest XML HttpRequest 是一种浏览器与服务器进行数据交换的…...

CPU与GPU的原理不同
CPU(中央处理器)和GPU(图形处理器)在设计原理上有很大的不同。CPU是通用的计算核心,擅长处理复杂的控制流和数据结构,而GPU则是为了并行处理大量相似的计算任务而设计的。二者是计算机系统中两种不同类型的…...

嵌入式相关基础
一.常见的芯片类型 1.微控制器(MCU) (1)STM32 主频(MHz)内核Flash(Kbytes)Ram(Kbytes)封装ADC channels DAC channels SPISTM32F407ZG168ARM Cortex-M4f1024192LQFP1442423STM32F407ZE168ARM Cortex-M4f512192LQFP1442423STM32F407VE168ARM Cortex-M4f512192LQFP1001623STM32…...

无线麦克风推荐哪些品牌?一文读懂家用无线麦克风哪个牌子好!
在这个充满创意与表达的时代,无线领夹麦克风以其独特的魅力,成为了声音创作者们的得力助手。它小巧便携,功能强大,无论是日常拍摄、直播互动还是专业演出,都能轻松应对,让你的声音随时随地清晰传递。那么…...

构建SOA架构时应该注意的问题
1.原有系统架构中的集成需求 面向服务的体系结构本质上来说是一种具有特殊性质的体系结构,它由具有互操作性和位置透明的组件集成构建并互连而成。基于SOA的企业系统架构通常都是在现有系统架构投资的基础上发展起来的,我们并不需要彻底重新开发全部的子…...

动手学深度学习(Pytorch版)代码实践 -深度学习基础-13Kaggle竞赛:2020加州房价预测
13Kaggle竞赛:2020加州房价预测 # 导入所需的库 import numpy as np import pandas as pd import torch import hashlib import os import tarfile import zipfile import requests from torch import nn from d2l import torch as d2l# 读取训练和测试数据 train_…...

编程输出中间变量:深度解析与实战应用
编程输出中间变量:深度解析与实战应用 在编程过程中,中间变量是一个至关重要的概念。它们不仅有助于我们更好地理解和组织代码,还能提高程序的效率和可读性。那么,编程输出中间变量究竟是什么呢?本文将从四个方面、五…...

冒泡排序、选择排序
冒泡排序 按照冒泡排序的思想,我们要把相邻的元素两两比较,当一个元素大于右侧相元素时,交换它们的位置;当一个元素小于或等于右侧相邻元素时,位置不变 大的往右丢(往下沉),小的往…...

嵌入式实训day6
1、 from machine import Pin from neopixel import NeoPixel import timeif __name__"__main__"#创建RBG灯带控制对象,包含5个像素(5个RGB LED)rgb_led NeoPixel(Pin(4,Pin.OUT),5)#定义RGB颜色RED(255,0,0)GREEN(0,2…...

产品经理是青春饭吗?终于有了答案!
不少考生疑惑产品经理是青春饭吗?产品经理能干到多少岁?弄清楚这些问题,我们才会有长久的规划。产品经理是青春饭吗?产品经理能干到多少岁?一起来看看 一、产品经理是青春饭吗? 产品经理是否吃青春饭需要…...
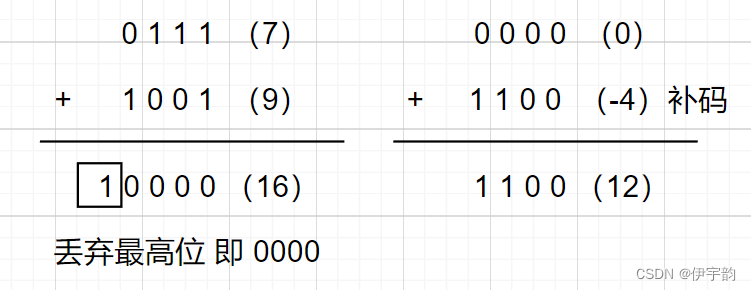
FPGA - 数 - 加减乘除
一,数的表示 首先,将二进制做如下解释: 2的0次方1 2的1次方2 2的2次方4 2的3次方8 ..... 以此类推,那么任何整数,或者说任意一个自然数均可以采用这种方式来表示。 例如,序列10101001,根据上述…...

软件性能测试之负载测试、压力测试详情介绍
负载测试和压力测试是软件性能测试中的两个重要概念,它们在保证软件质量和性能方面起到至关重要的作用,本文将从多个角度详细介绍这两种测试类型。 一、软件负载测试 负载测试是在特定条件下对软件系统进行长时间运行和大数据量处理的测试ÿ…...

科研辅助工具
科研工具收集 1. 如何筛选出最合适的SCI论文投稿杂志:点击直达 2. 分享三种正确查找期刊全称、缩写的网站: 点击直达...

亿达中国武汉园区入选“武汉市科技金融工作站”及“武汉市线下首贷服务站”
近日,武汉市2024科技金融早春行活动在深交所湖北资本市场培育基地举行。会上,第四批武汉市科技金融工作站试点单位名单及第五批武汉地区金融系统线下首贷服务站名单正式公布,武汉软件新城成功入选上述两个名单。 为缓解科技型企业融资难题&a…...
)
Docker配置阿里云加速器(2续)
默认情况下镜像是从docker hub下载,由于docker hub服务器在国外,由于网络原因镜像下载速度较慢,一般会配置镜像加速进行下载 国内镜像加速器有阿里云、网易云、中科大等,本章配置阿里云镜像加速器,速度较快 镜像加速源 镜像加速器 镜像加速器地址 <...

我用chatgpt写了一款程序
众所周知,Chatgpt能够帮助人们写代码,前几天苏音试着完全用Chatgpt写一款Python程序 有一句话我很赞同,未来能代替人的不是AI,是会使用AI的人。 最终,写下来效果还不错,完全提升了我的办公效率。 开发前…...

RocketMQ延迟消息机制
两种延迟消息 RocketMQ中提供了两种延迟消息机制 指定固定的延迟级别 通过在Message中设定一个MessageDelayLevel参数,对应18个预设的延迟级别指定时间点的延迟级别 通过在Message中设定一个DeliverTimeMS指定一个Long类型表示的具体时间点。到了时间点后…...

安宝特方案丨XRSOP人员作业标准化管理平台:AR智慧点检验收套件
在选煤厂、化工厂、钢铁厂等过程生产型企业,其生产设备的运行效率和非计划停机对工业制造效益有较大影响。 随着企业自动化和智能化建设的推进,需提前预防假检、错检、漏检,推动智慧生产运维系统数据的流动和现场赋能应用。同时,…...

解决Ubuntu22.04 VMware失败的问题 ubuntu入门之二十八
现象1 打开VMware失败 Ubuntu升级之后打开VMware上报需要安装vmmon和vmnet,点击确认后如下提示 最终上报fail 解决方法 内核升级导致,需要在新内核下重新下载编译安装 查看版本 $ vmware -v VMware Workstation 17.5.1 build-23298084$ lsb_release…...

React Native在HarmonyOS 5.0阅读类应用开发中的实践
一、技术选型背景 随着HarmonyOS 5.0对Web兼容层的增强,React Native作为跨平台框架可通过重新编译ArkTS组件实现85%以上的代码复用率。阅读类应用具有UI复杂度低、数据流清晰的特点。 二、核心实现方案 1. 环境配置 (1)使用React Native…...

服务器硬防的应用场景都有哪些?
服务器硬防是指一种通过硬件设备层面的安全措施来防御服务器系统受到网络攻击的方式,避免服务器受到各种恶意攻击和网络威胁,那么,服务器硬防通常都会应用在哪些场景当中呢? 硬防服务器中一般会配备入侵检测系统和预防系统&#x…...

屋顶变身“发电站” ,中天合创屋面分布式光伏发电项目顺利并网!
5月28日,中天合创屋面分布式光伏发电项目顺利并网发电,该项目位于内蒙古自治区鄂尔多斯市乌审旗,项目利用中天合创聚乙烯、聚丙烯仓库屋面作为场地建设光伏电站,总装机容量为9.96MWp。 项目投运后,每年可节约标煤3670…...

2025 后端自学UNIAPP【项目实战:旅游项目】6、我的收藏页面
代码框架视图 1、先添加一个获取收藏景点的列表请求 【在文件my_api.js文件中添加】 // 引入公共的请求封装 import http from ./my_http.js// 登录接口(适配服务端返回 Token) export const login async (code, avatar) > {const res await http…...

Linux云原生安全:零信任架构与机密计算
Linux云原生安全:零信任架构与机密计算 构建坚不可摧的云原生防御体系 引言:云原生安全的范式革命 随着云原生技术的普及,安全边界正在从传统的网络边界向工作负载内部转移。Gartner预测,到2025年,零信任架构将成为超…...

Module Federation 和 Native Federation 的比较
前言 Module Federation 是 Webpack 5 引入的微前端架构方案,允许不同独立构建的应用在运行时动态共享模块。 Native Federation 是 Angular 官方基于 Module Federation 理念实现的专为 Angular 优化的微前端方案。 概念解析 Module Federation (模块联邦) Modul…...

【决胜公务员考试】求职OMG——见面课测验1
2025最新版!!!6.8截至答题,大家注意呀! 博主码字不易点个关注吧,祝期末顺利~~ 1.单选题(2分) 下列说法错误的是:( B ) A.选调生属于公务员系统 B.公务员属于事业编 C.选调生有基层锻炼的要求 D…...
