Scikit-Learn支持向量机回归
Scikit-Learn支持向量机回归
- 1、支持向量机回归
- 1.1、最大间隔与SVM的分类
- 1.2、软间隔最大化
- 1.3、支持向量机回归
- 1.4、支持向量机回归的优缺点
- 2、Scikit-Learn支持向量机回归
- 2.1、Scikit-Learn支持向量机回归API
- 2.2、支持向量机回归初体验
- 2.3、支持向量机回归实践(加州房价预测)
1、支持向量机回归
支持向量机(Support Vector Machine,SVM)算法既可以用于回归问题(SVR),也可以用于分类问题(SVC)。通常情况下,SVM用于分类问题,但后来也被扩展用于回归问题。SVM(回归)在机器学习知识结构中的位置如下:
1.1、最大间隔与SVM的分类
SVM是一种二分类模型,它的基本模型是定义在特征空间上的间隔最大的线性分类器,他的学习策略就是间隔最大化
如图所示,三条直线分别代表三个SVM分类器,请问哪一个分类器比较好?

凭直观感受答案应该是H3。首先H1不能把类别分开;H2可以,但分割线与最近的数据点只有很小的间隔,如果测试数据有一些噪声的话可能就会被H2错误分类(即对噪声敏感、泛化能力弱)。H3以较大间隔将它们分开,这样就能容忍测试数据的一些噪声,是一个泛化能力不错的分类器
对于支持向量机来说,数据点若是p维向量,我们用p−1维的超平面来分开这些点。但是可能有许多超平面可以把数据分类。最佳超平面的一个合理选择就是以最大间隔把两个类分开的超平面。因此,SVM选择能够使离超平面最近的数据点的到超平面距离最大的超平面
以上介绍的SVM只能解决线性可分的问题,为了解决更加复杂的问题,支持向量机学习方法由简至繁可分为三类:
-
线性可分SVM
当训练数据线性可分时,通过硬间隔(Hard Margin)最大化学习一个线性的分类器,即线性可分支持向量机(亦称作硬间隔支持向量机)
-
线性SVM
当训练数据不能线性可分但是可以近似线性可分时,通过软间隔(Soft Margin)最大化学习一个线性的分类器,即线性支持向量机(又称作软间隔支持向量机)
-
非线性SVM
当训练数据线性不可分时,通过使用核技巧(Kernel Trick)及软间隔最大化可以学习非线性支持向量机,等价于隐式地在高维特征空间中学习线性支持向量机
1.2、软间隔最大化
在实际应用中,完全线性可分(硬间隔)的情况非常少见。例如下面的分类图,我们没有办法找到一条直线,把空间划分为2个区域,因此,要对其进行切分,有以下两种方案:
1)仍然使用直线,不过不追求完全可分,适当包容一些分错的情况(线性SVM)

在这个过程中,我们会在模型中加入惩罚函数,尽量让分错的点不要太多。对分错点的惩罚函数就是这个点到其正确位置的距离
如上图所示,黄色、蓝色的直线分别为支持向量所在的边界,黑色的线为决策函数,那些绿色的线表示分错的点到其相应的决策面的距离,这样我们可以在原函数上面加上一个惩罚函数,并且带上其限制条件为:

上式为在线性可分问题的基础上加上的惩罚函数部分,当 x i x_i xi在正确一边的时候, ε i \varepsilon_i εi=0,R为全部的样本点的数目,C是惩罚系数
- 当C很大的时候,分错的点就会更少,但是过拟合的情况可能会比较严重
- 当C很小的时候,分错的点可能会很多,不过可能由此得到的模型也会不太正确
C越小对误分类的惩罚越小,C越大对误分类的惩罚越大,当C取正无穷时就变成了硬间隔优化。C越小越容易欠拟合,C越大越容易过拟合。实际应用中我们也会调整和选择合适的C值
2)用曲线将其完全分开,即非线性的决策边界(非线性SVM)

如果我们要处理的分类问题更加复杂,甚至不能像上面一样近似线性可分,这种情况下找到的超平面分错的程度太高,是不可接受的
对于这样的问题,解决的方案是将样本从原始空间映射到一个更高维的特征空间,使得样本在这个特征空间内线性可分,然后再运用SVM求解。这个映射的函数称为核函数

更多关于软间隔与硬间隔、SVM的损失函数、核函数以及SVM分类的介绍详见文章:传送门
1.3、支持向量机回归
支持向量机回归的核心思想是通过最小化预测误差来拟合数据,并且在拟合过程中保持一个边界(间隔),使得大部分数据点都落在这个边界之内。SVR与分类问题中的支持向量机(SVC)类似,但其目标是拟合数据而不是分离数据
在SVC中,在数据集线性可分的情况下,训练数据集的样本点中与分离超平面距离最近的数据点称为支持向量(Support Vector)

即所有在直线 ω X \omega X ωX+ b b b= 1 1 1和直线 ω X \omega X ωX+ b b b= − 1 -1 −1上的点。在决定最佳超平面时只有支持向量起作用,而其他数据点并不起作用
与SVC类似,在SVR中,我们同样定义一个边界,由一个中心线和两个平行的边界线组成。这些边界线之间的距离称为间隔,它由用户预先设定。SVR的目标是找到一个函数,使得大部分数据点都落在间隔内,并
相关文章:

Scikit-Learn支持向量机回归
Scikit-Learn支持向量机回归 1、支持向量机回归1.1、最大间隔与SVM的分类1.2、软间隔最大化1.3、支持向量机回归1.4、支持向量机回归的优缺点2、Scikit-Learn支持向量机回归2.1、Scikit-Learn支持向量机回归API2.2、支持向量机回归初体验2.3、支持向量机回归实践(加州房价预测…...

ElasticSearch的桶聚合
桶聚合 在前面几篇博客中介绍的聚合指标是指符合条件的文档字段的聚合,有时还需要根据某些维度进行聚合。例如在搜索酒店时,按照城市、是否满房、标签和创建时间等维度统计酒店的平均价格。这些字段统称为“桶”,在同一维度内有一个或者多个桶。例如城市桶,有“北京”、“天…...
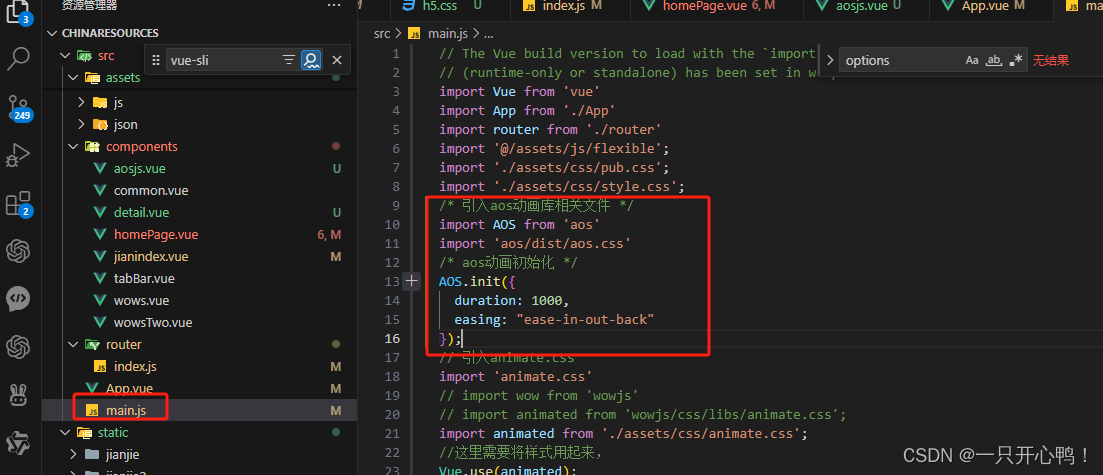
vue引入aos.js实现滚动动画
aos.js官方网站:http://michalsnik.github.io/aos/ aos.js介绍 AOS (Animate on Scroll) 是一个轻量级的JavaScript库,用于实现当页面元素随着用户滚动进入可视区域时触发动画效果。它不需要依赖 jQuery,可以很容易地与各种Web开发框架&#…...

python+selenium之点击元素报错:‘NoneType‘ object has no attribute ‘click‘
今日遇到一个很奇怪的问题 case1:当使用顺序结构直接从登录到点击页面菜单,则可以正常点击菜单 case2:若把登录分离开,采用封装的方法点击菜单则会提示:‘NoneType’ object has no attribute ‘click’ 具体页面如下,…...

Web 品质国际化
Web 品质国际化 随着互联网的普及和全球化的推进,Web品质国际化已成为现代企业发展的必然趋势。Web品质国际化不仅仅是网站的多语言支持,更是一种全面的文化、技术和市场适应性的体现。本文将探讨Web品质国际化的概念、重要性以及实施策略。 一、Web品质国际化的概念 Web品…...
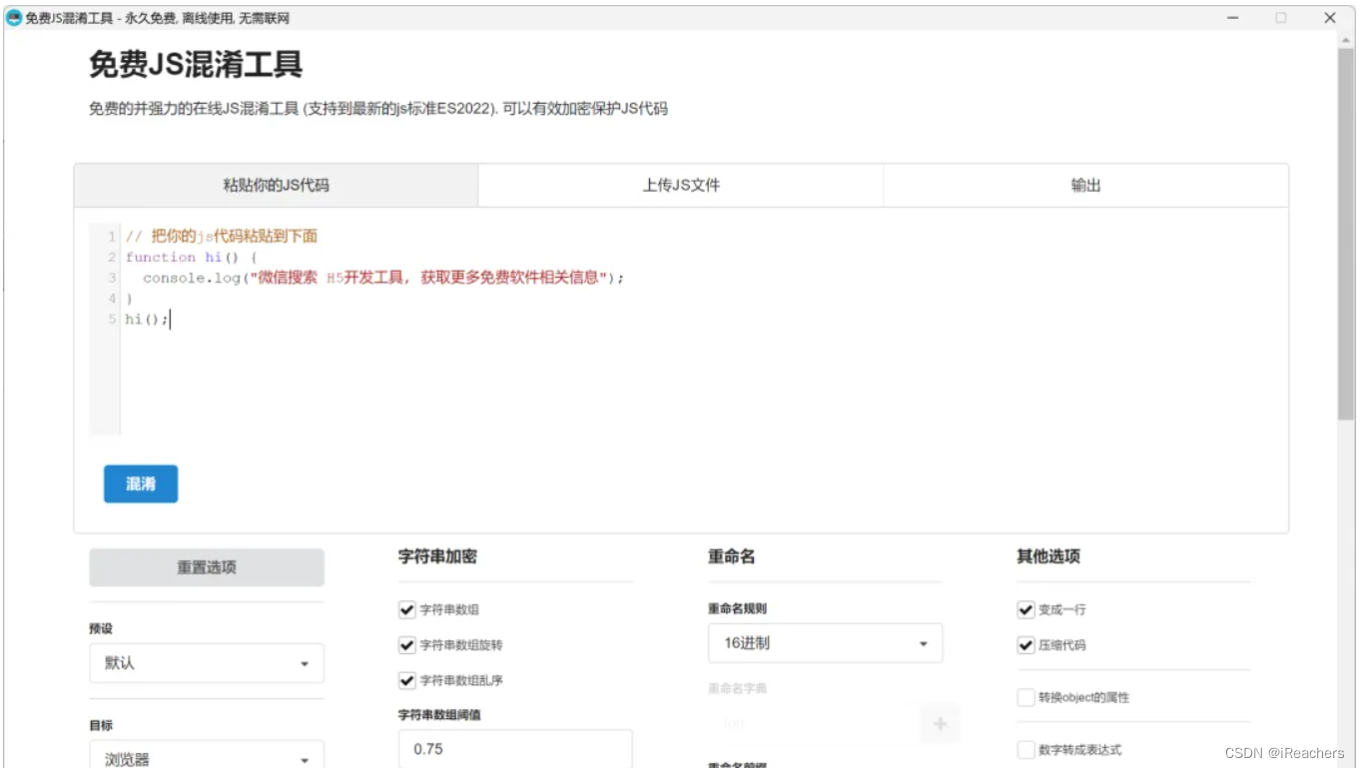
绿色免费离线版JS加密混淆工具 - 支持全景VR加密, 小程序js加密, H5网站加密
自从我们推出在线版的免费JS加密混淆工具以来,受到了广大用户的热烈欢迎。特别是全景开发人员,他们使用该工具加密VR插件的JS代码, 添加域名锁等,都非常有效地保护了插件的代码资源。 最近,我们收到了许多用户的反馈,…...

文心一言 VS 讯飞星火 VS chatgpt (284)-- 算法导论21.2 2题
二、对定理 21.1 的整体证明进行改造,得到使用链表表示和加权合并启发式策略下的 MAKE-SET 和 FIND-SET 的摊还时间上界为 O(1),以及 UNION 的摊还时间上界为 O(lgn)。如果要写代码,请用go语言。 文心一言: 在Go语言中实现使用链…...

计算机组成原理网课笔记2
存储系统基本概念...
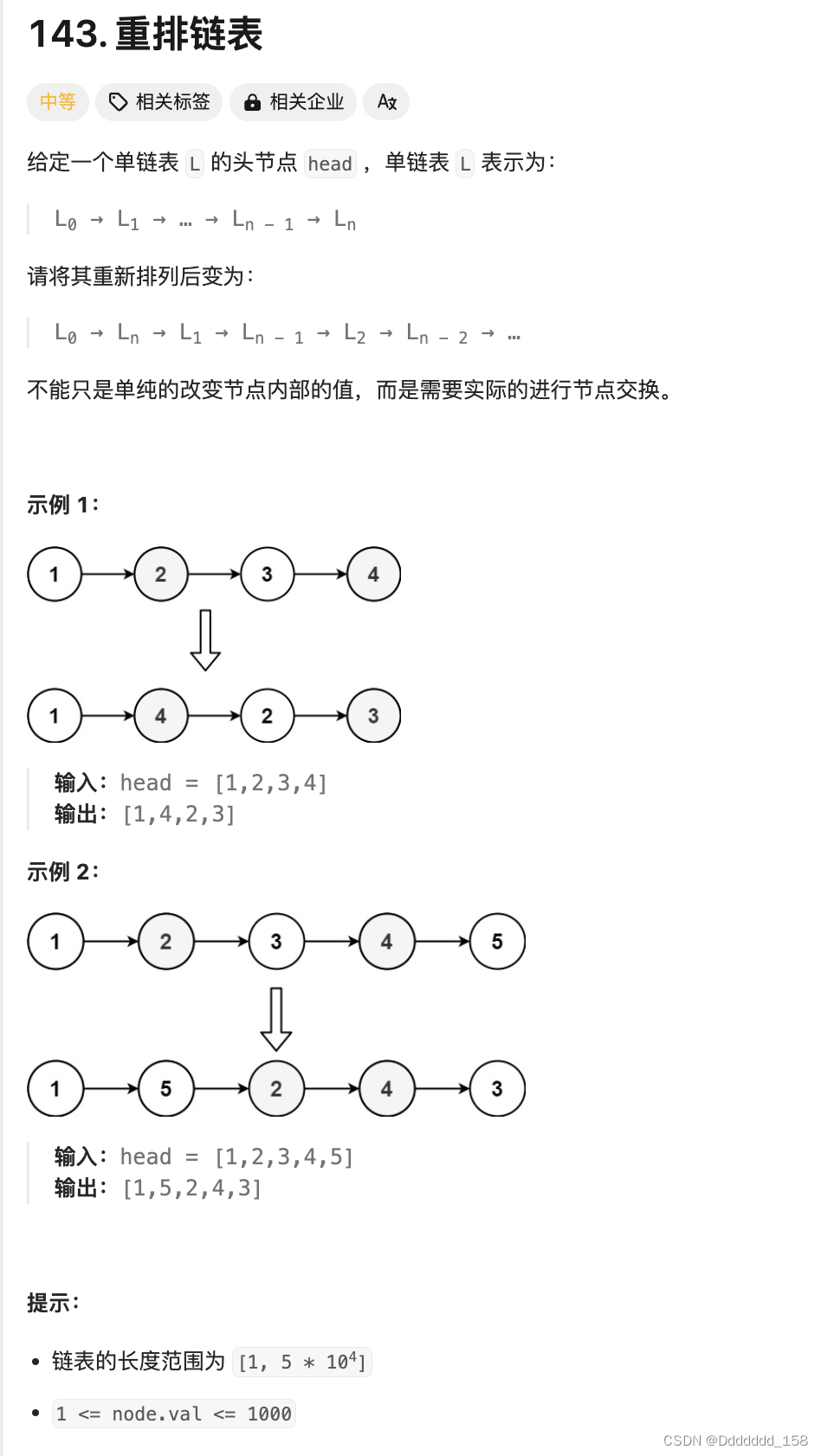
C++ | Leetcode C++题解之第143题重排链表
题目: 题解: class Solution { public:void reorderList(ListNode* head) {if (head nullptr) {return;}ListNode* mid middleNode(head);ListNode* l1 head;ListNode* l2 mid->next;mid->next nullptr;l2 reverseList(l2);mergeList(l1, l…...

手写一个JSON可视化工具
前言 JSON 平时大家都会用到,都不陌生,今天就一起来实现一个 JSON 的可视化工具。 大概长成下面的样子: 树展示 相比于现有的一些 JSON 格式化工具,我们今天制作的这个小工具会把 JSON 转为树去表示。其中: 橙色标…...
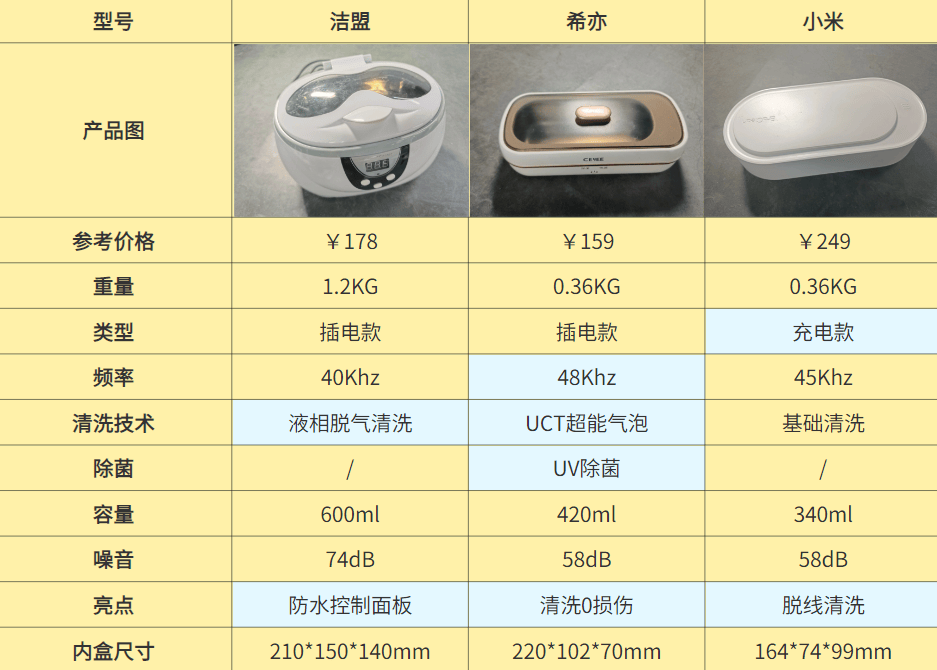
洁盟超声波清洗机怎么样?2024爆款机型声波清洗机测评、一篇看懂
随着现在近视率的逐年上升,戴眼镜的人群越来越多!当然他们也在面临着一个眼镜清洗的问题!因为长期佩戴眼镜,镜框还有镜片上面都是会积累灰尘、油污、污垢以及细菌,脏脏的不仅令眼镜不美观,同时在长期的佩戴…...

react 自定义鼠标右键点击事件
功能:鼠标右键点击节点时,出现“复制”功能,点击其他部位,隐藏“复制”;鼠标右键事件的文案,始终在鼠标点击位置的右下方;点击复制,提示复制成功 效果图: 代码࿱…...

make V=1 分析
文章目录 make V1 make V1 # 顶层 Makefile 580 -include include/config/auto.conf 584 -include include/config/auto.conf.cmd ...... 593 include/config/%.conf: $(KCONFIG_CONFIG) include/config/auto.conf.cmd 594 $(Q)$(MAKE) -f $(srctree)/Makefile syncconfig 595…...
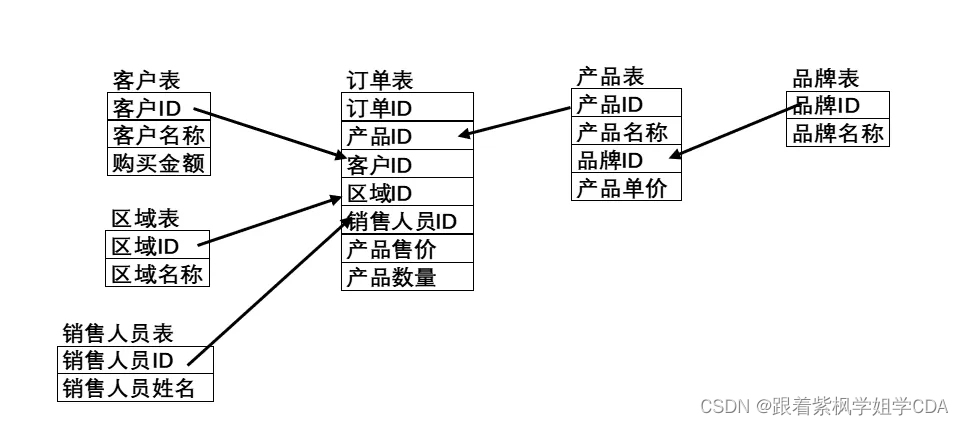
每天一个数据分析题(三百五十八)-图表决策树
图中是某公司记录销售情况相关的表建立好的多维分析模型,请根据模型回答以下问题: 1)该模型属于哪种连接模式? A. 星型模式雪花模式 B. 星座模式雪花模式 C. 星座模式星型模式雪花模式 D. 以上都不对 数据分析认证考试介绍…...

HarmonyOS 页面路由(Router)
1. HarmonyOS页面路由(Router) 页面路由指在应用程序中实现不同页面之间的跳转和数据传递。HarmonyOS提供了Router模块,通过不同的url地址,可以方便地进行页面路由,轻松地访问不同的页面。本文将从页面跳转、页面返回和页面返回前增加一个询问…...

Python 正则表达式语法
Python 中的正则表达式是通过 re 模块提供的,它支持大多数正则表达式的语法。以下是一些基本的正则表达式语法元素: 字符匹配: . 匹配任意单个字符,除了换行符。\d 匹配任意数字,等同于 [0-9]。\D 匹配任意非数字字符,…...

计算机专业毕设-校园二手交易平台
1 项目介绍 基于SpringBoot的校园二手交易平台:前端Freemarker,后端 SpringBoot、Jpa,系统用户分为两类,管理员、学生,具体功能如下: 管理员: 基本功能:登录、修改个人信息、修改…...
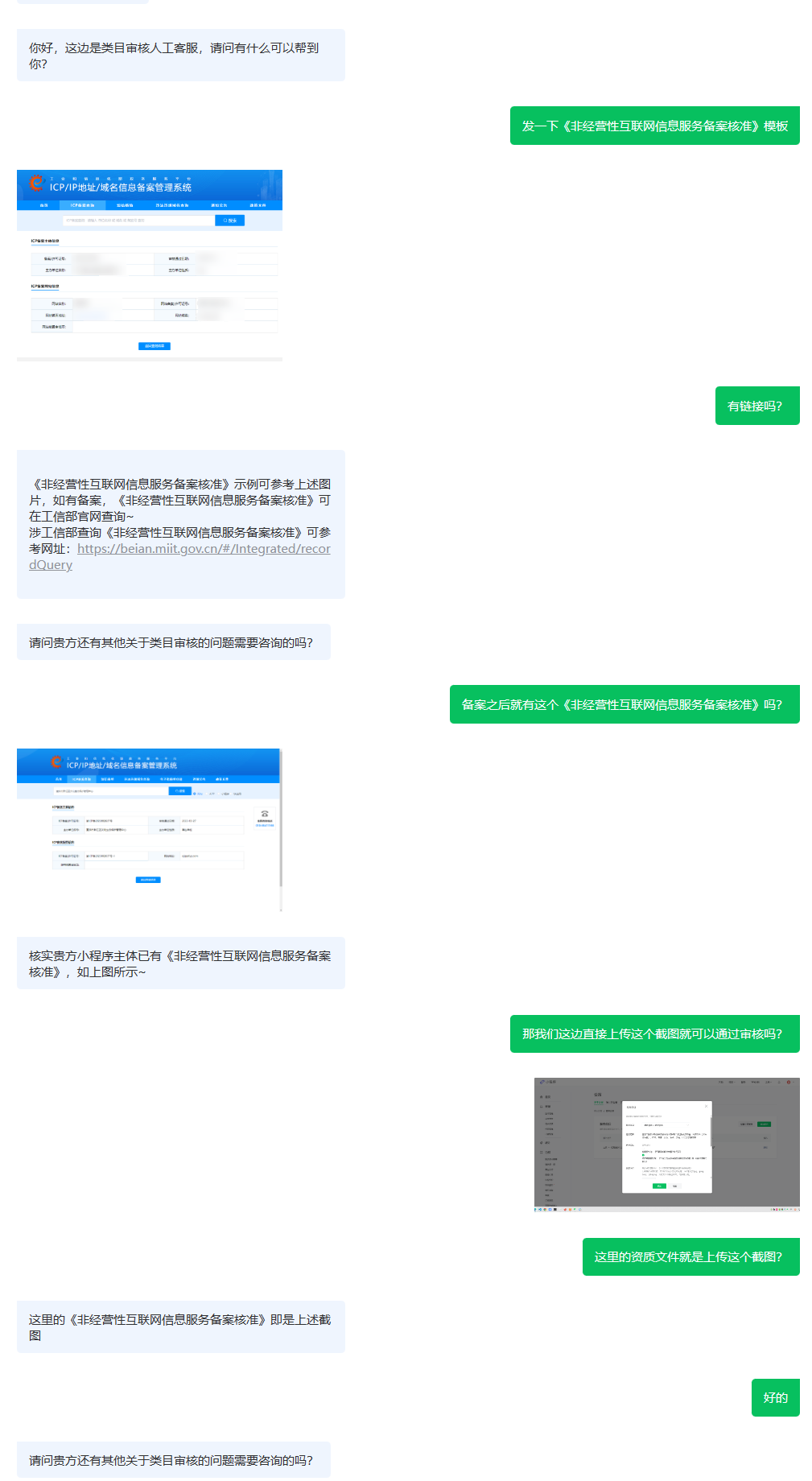
微信小程序添加服务类目|《非经营性互联网信息服务备案核准》怎么获取
根据客服反馈,《非经营性互联网信息服务备案核准》在工业和信息化部政务服务平台网站查询,查询结果的截图就是《非经营性互联网信息服务备案核准》。 工业和信息化部政务服务平台 《非经营性互联网信息服务备案核准》: 与客服聊天的截图&a…...
Internet Download Manager ( 极速下载器 ) 序列号注册码 IDM下载器注册机中文激活破解版
IDM下载器(Internet Download Manager)是一款专业的下载管理软件,它通过多线程技术和智能文件分段技术,有效提升下载速度,并支持断点续传,还具有计划下载功能,用户可以设置特定的下载时间,非常适合需要在特…...

FPGA - 滤波器 - IIR滤波器设计
一,IIR滤波器 在FPGA - 滤波器 - FIR滤波器设计中可知,数字滤波器是一个时域离散系统。任何一个时域离散系统都可以用一个N阶差分方程来表示,即: 式中,x(n)和y(n)分别是系统的输入序列和输出序列;aj和bi均为…...

利用最小二乘法找圆心和半径
#include <iostream> #include <vector> #include <cmath> #include <Eigen/Dense> // 需安装Eigen库用于矩阵运算 // 定义点结构 struct Point { double x, y; Point(double x_, double y_) : x(x_), y(y_) {} }; // 最小二乘法求圆心和半径 …...

地震勘探——干扰波识别、井中地震时距曲线特点
目录 干扰波识别反射波地震勘探的干扰波 井中地震时距曲线特点 干扰波识别 有效波:可以用来解决所提出的地质任务的波;干扰波:所有妨碍辨认、追踪有效波的其他波。 地震勘探中,有效波和干扰波是相对的。例如,在反射波…...

7.4.分块查找
一.分块查找的算法思想: 1.实例: 以上述图片的顺序表为例, 该顺序表的数据元素从整体来看是乱序的,但如果把这些数据元素分成一块一块的小区间, 第一个区间[0,1]索引上的数据元素都是小于等于10的, 第二…...

遍历 Map 类型集合的方法汇总
1 方法一 先用方法 keySet() 获取集合中的所有键。再通过 gey(key) 方法用对应键获取值 import java.util.HashMap; import java.util.Set;public class Test {public static void main(String[] args) {HashMap hashMap new HashMap();hashMap.put("语文",99);has…...

Keil 中设置 STM32 Flash 和 RAM 地址详解
文章目录 Keil 中设置 STM32 Flash 和 RAM 地址详解一、Flash 和 RAM 配置界面(Target 选项卡)1. IROM1(用于配置 Flash)2. IRAM1(用于配置 RAM)二、链接器设置界面(Linker 选项卡)1. 勾选“Use Memory Layout from Target Dialog”2. 查看链接器参数(如果没有勾选上面…...

Java-41 深入浅出 Spring - 声明式事务的支持 事务配置 XML模式 XML+注解模式
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

多种风格导航菜单 HTML 实现(附源码)
下面我将为您展示 6 种不同风格的导航菜单实现,每种都包含完整 HTML、CSS 和 JavaScript 代码。 1. 简约水平导航栏 <!DOCTYPE html> <html lang"zh-CN"> <head><meta charset"UTF-8"><meta name"viewport&qu…...

浅谈不同二分算法的查找情况
二分算法原理比较简单,但是实际的算法模板却有很多,这一切都源于二分查找问题中的复杂情况和二分算法的边界处理,以下是博主对一些二分算法查找的情况分析。 需要说明的是,以下二分算法都是基于有序序列为升序有序的情况…...

【JavaWeb】Docker项目部署
引言 之前学习了Linux操作系统的常见命令,在Linux上安装软件,以及如何在Linux上部署一个单体项目,大多数同学都会有相同的感受,那就是麻烦。 核心体现在三点: 命令太多了,记不住 软件安装包名字复杂&…...

LeetCode - 199. 二叉树的右视图
题目 199. 二叉树的右视图 - 力扣(LeetCode) 思路 右视图是指从树的右侧看,对于每一层,只能看到该层最右边的节点。实现思路是: 使用深度优先搜索(DFS)按照"根-右-左"的顺序遍历树记录每个节点的深度对于…...
