【算法与设计】期末总结
文章目录
- 第一章 概述
- 算法与程序
- 时间复杂性
- 求上界
- 第二章 递归与分治
- 双递归函数——Ackerman函数
- 分治策略
- 大整数乘法
- 两位×两位
- 四位x四位
- 三位x三位
- 两位x六位
- 第三章 动态规划
- 矩阵连乘
- 基本要素
- 最优子结构
- 子问题重叠
- 备忘录
- 第四章 贪心算法
- 活动安排问题
- 基本要素
- 贪心选择性质
- 最优子结构性质
- 与动态规划的区别
- 背包问题
- 物体可分
- 物体不可分
- 第五章 回溯法
- **问题的解空间**
- 0-1背包
- 迭代回溯
- 0-1背包问题(树结构)
- 期末考点
第一章 概述
算法与程序
算法:解决问题的一种方式或者一种过程。算法有若干个指令组成的有穷序列。
程序:算法用某种程序设计语言的具体实现
算法的4种性质:
- 输入
- 输出
- 确定性
- 有限性
程序可以不满足“有限性”
时间复杂性
算法复杂度的高低体现在运行该算法所需要的计算机资源的多少上。资源的多少依赖于要解决问题的规模(N)、算法的输入(I)和算法本身的函数(A)
关于时间复杂性,分为三种情况:最坏情况、最好情况和平均情况。
可操作性最好且最有实际价值的是最坏情况的时间复杂度。
求上界
当N>=N0时有f(N)<=Cg(N),称为函数f(N)的一个上界是Cg(N),记作f(N)=O(g(N))
这个上界的阶越低,则评估越精确,结果越有价值
如何求上界?
1.把f(N)函数中的所有阶放大到最高阶,合并后并记为Cg(N)
2.此时f(N)<=Cg(N),把这两个函数去化简即可得条件,即n值。
例子:f(n)=3n2+10n
最高阶是n2,所有阶放大到最高阶得3n2+10n2=13n2,记为Cg(N)
此时,C=13,g(N)=n2
当3n2+10n <= 3n2+10n2时,即10n <= 10n2时,条件成立。
故n0>=1
综上,当n0=1时,C=13,f(n)=O(n2)
注意:放大方向不变,方式可以改变(即可以增大阶层且缩小系数),如3n2+10n <= 3n2+n2,此时结果的C和n0都不一样,但f(n)始终一样。
第二章 递归与分治
递归:代码效率好,但是空间效率和时间效率差
如何改进??
消除递归,有两种方式:阶乘(循环)和阶加(循环、通项公式)
双递归函数——Ackerman函数
定义:一个函数及它的一个变量由函数自身定义时
分治策略
基本思想:将问题分解为k个小规模的子问题,这些子问题相互独立且原问题相同。递归地解这些子问题,将个子问题的解合并得到原问题的解。
大整数乘法
普通乘法的时间复杂度是O(n2)
通过分支策略可达到O(n1.59)
两位×两位
步骤:
1.两位数分出高低位
2.套用公式求p,q,r
遇到负数,高低位都带符号
如-23:高位-2,低位-2。至此,-23=(-2)*10+(-3)
最简的分治(递归出口):一位x一位
四位x四位
一直递归,直到满足出口
三位x三位
往前补0,公式不变
两位x六位
补零或者把六位拆成3个两位
第三章 动态规划
| 动态规划 | 分治 | |
|---|---|---|
| 同 | 分解子问题 | 分解子问题 |
| 异 | 子问题相互依赖 | 子问题相互独立 |
基本思想:
分解成子问题求解时,有些子问题被重复计算许多次。用一个表来记录所有已解决的子问题的答案,而在需要时再找出已求得的答案,就可以避免大量的重复计算。
步骤:
1.找到最优解,刻画其结构性质
2.递归地定义最优值
3.以自底向上的方式计算最优值
4.根据计算最优值时得到的信息,构造最优解
矩阵连乘
题目背景:
若两矩阵相乘,需满足第一矩阵的行=第二矩阵的列
即Amxn X Bpxq的条件为n==p
此时,乘法次数为=m x n x q
连乘次序会影响乘法次数
按照上述步骤:
1.最优解及其结构性质:最小乘法次数 及 最小乘法次数的断开处
记A[i:j]是AiAi+1…Aj
问题:A[1:n],可以在k=1,2,⋯n−1处断开,若A[1:n]最优,则A[1:k]与A[k+1:n]也最优
2.建立递归关系
记A[i:j],其中1≤i≤j≤n,最少乘法次数记m[i][j]
(1)当i=j时→ A[i:i] →指A[i] 本身→乘法次数为0,即 m[i][j]=0
(2)当i<j时, 在k处断开, k可以取值i, i+1, ∙∙∙, j−1,在某k处乘法次数最少
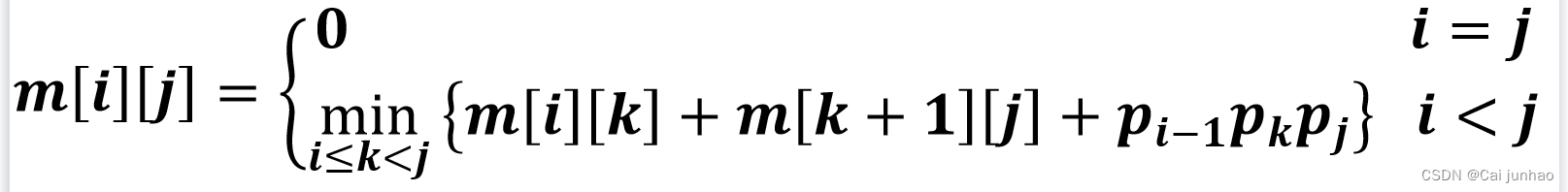
定义数组p存储矩阵信息
p[0]为第1矩阵的行
p[1]为第1矩阵列(也为第2矩阵行)
p[2]为第2矩阵列(也为第3矩阵行)
p[3]为第3矩阵列(也为第4矩阵行)
…
p[n]为第n矩阵列
3.计算最优值
对于结果的存储,使用m表存储最小乘法次数(即最优值),用s表存储k值(即最优解)
代码实现:
//构造最优值
void MatrixChain(int *p, int n, int **m, int **s)//P一维数组记下标;n矩阵个数;m表;s记分段
{for(int i=1;i<=n;i++)m[i][i]=0;//对角线上都填0for(int r=2;r<=n;r++)//在m表中,从第2条填到第n条(对角线)for(int i=1;i<=n-r+1;i++)//i是行下标,从第1行开始填一个倒三角的表{int j=i+r-1;//列下标m[i][j]=0+m[i+1][j]+p[i-1]*p[i]*p[j];//实现递归计算,先初始化第1项,省略了m[i][i]s[i][j]=i;//s记分段点,此为s的初值for(int k=i+1;k<j;k++)//递归式从k=i+1到j-1,找最小{int t=m[i][k]+m[k+1][j]+p[i-1]*p[k]*p[j];//递归式计算 if(t<m[i][j]){m[i][j]=t;//记入最小值s[i][j]=k;//记入划分位置}}}
}4.构造最优解
算法MatrixChain只是计算出了最优值,并未给出最优解。但是MatrixChain已记录了构造最优解所需要的全部信息。s[i][j]中的数表明,最佳方式应在矩阵的何处断开。
//构造最优解
void Traceback(int i,int j,int **s)//求A[i:j]的最优解构造,利用s[][],设已知s[i][j]=k
{if(i==j)return ;//A[i:i]不必构造,递归出口Traceback(i,s[i][j],s);//求A[i:k]的构造,记1Traceback(s[i][j]+1,j,s);//求A[k+1:j]的构造,记2cout<<"Multiply A["<<i<<":"<<s[i][j]<<"]and A["<<(s[i][j]+1)<<":"<<j<<"]"<<endl;//输出Ai,k And Ak+1,j,表明在k处断开,记3
}
基本要素
最优子结构
设计动态规划算法的第一步通常是要刻画最优解的结构。
当问题的最优解包含了其子问题的最优解时,称该问题具有最优子结构性质。
子问题重叠
在用递归算法自顶向下解此问题时,每次产生的子问题并不总是新问题,有些子问题被反复计算多次。
动态规划算法正是利用了这种子问题的重叠性质,对每一个子问题只解一次,而后将其解保存在一个表格中,当再次需要解此子问题时,只是简单地用常数时间查看一下结果。
备忘录
动态规划的变形——备忘录
动态规划:保存所有子问题的解
变形:动态规划是自底向上;备忘录是自顶向下
第四章 贪心算法
工作量:贪心算法 < 动态规划
但是贪心算法的结果可能不是最优结果,因为贪心算法并不是从整体最优上加以考虑,它所做出的选择只是某种意义上的局部最优选择
所以,贪心算法的关键是贪心策略的选择。
活动安排问题
该问题要求高效地安排一系列争用某一个公共资源的活动。有n个活动,开始和结束的时间si≤fi,如何安排最多个活动?
贪心策略:按结束时间递增排序,从前向后能安排则安排
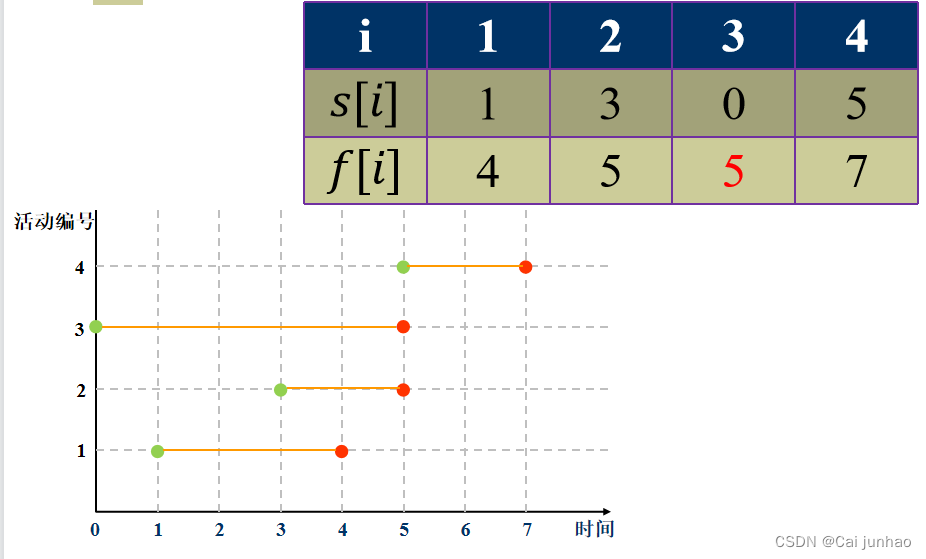
例题:当前有4个活动。
| i | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| s[i] | 1 | 3 | 0 | 5 |
| f[i] | 4 | 5 | 6 | 7 |
若选择最早结束优先,能使选入活动最多
若最早开始优先,仅能安排这一个活动
若最短占用优先,则能安排这一个活动
推广:
假设要在足够多的的会场里安排一批活动,即每个活动都要被安排,并希望使用尽可能少的会场。
(1)贪心策略思路1:先在第1会场安排最多活动,其次在第2会场安排最多,……,依此类推 。
(2)贪心策略思路2:视为区间重叠问题。时间点:起点和终点。
按时间点排序起点分配1个会场,终点回收,保证此会场可重复利用

基本要素
贪心选择性质
贪心选择性质是指所求问题的整体最优解是可以通过局部最优的选择,即贪心选择达到的。
在动态规划算法中,每步所做的选择往往依赖于相关子问题的解。因而只有在解出相关子问题后,才能做出选择。
而在贪心算法中,仅在当前状态下做出最好选择,即局部最优选择。然后再去解做出这个选择后产生的相应子问题。
最优子结构性质
最优子结构性质是该问题可用动态规划算法或贪心算法求解的关键特征。
与动态规划的区别
**贪心算法:**先依据贪心策略选择并解一个子问题,再进行下一步。
**动态规划算法:**先解决所有的子问题,比较得出一个最优子问题,再进行下一步。
背包问题
问题描述:容量为c的背包,有n种物品,每种物品重w_i,价值为v_i,其中1≤i≤n,
物品不可(可以)分开。
问:如何装入使价值最大?
| c | n | w1 | w2 | w3 | v1 | v2 | v3 |
|---|---|---|---|---|---|---|---|
| 50 | 3 | 10 | 20 | 30 | 60 | 100 | 120 |
物体可分
c>0,wi>0,vi>0,1≤i≤n。找(x1,x2,⋯,xn),0≤xi≤1,可为分数,即仅取一部分,
使 ∑ i = 1 n w i ∗ x i < = c \sum_{i=1}^{n} wi*xi<= c i=1∑nwi∗xi<=c 达到最大
∑ i = 1 n v i ∗ x i \sum_{i=1}^{n} vi*xi i=1∑nvi∗xi
//物品可分:贪心算法
#include <iostream>
#include <iomanip>
using namespace std;void Knapsack(int n, int c, int*v, int *w, double *x);int main()
{ int n=3;//物品数量 int c=50;//背包容量 int *v=new int[n+1];//价值 int *w=new int[n+1];//重量 int i;double *x=new double[n+1]; for(i=1;i<=n;i++)x[i]=0; //将数据按贪心策略排序 v[1]=60;v[2]=100;v[3]=120;w[1]=10;w[2]=20;w[3]=30;Knapsack(n,c,v,w,x); for(i=1;i<=n;i++){ if(x[i]>0)cout<<"物品"<<i<<"装入"<<setiosflags(ios::fixed)<<setprecision(2)<<x[i]<<endl;elsecout<<"物品"<<i<<"不装入"<<endl;}return 0;
}void Knapsack(int n, int c, int*v, int *w, double *x)
{int i;for(i=1;i<=n;i++){if(w[i]>c)break;else{x[i]=1;c=c-w[i]; } } if(i<=n) x[i]=(double)c/w[i];
}
step1:准备
按单位价格递减排序,x[ ]初值为0,先都没选
step2:循环
按递减装入物品至不可装为止,从1检查到n
物品装入置x[i]=1,c=c−w[i]
step3:最后
将当前i物品分开,送入c/w[i]
物体不可分
其中,c>0,wi>0,vi>0,1≤i≤n,
找(x1,x2,⋯,xn),xi∈{0,1},
(物品没装xi=0,装入xi=1)
使 ∑ i = 1 n w i ∗ x i < = c \sum_{i=1}^{n} wi*xi<= c i=1∑nwi∗xi<=c 达到最大
∑ i = 1 n v i ∗ x i \sum_{i=1}^{n} vi*xi i=1∑nvi∗xi
根据上述步骤:
1.最优子结构性质:
若(y_1,y_2,⋯,y_n)是最优解,则(y_2,⋯,y_n)是子问题的最优解
2.递归关系
m(i,j)记背包容量j,可选物品为i,i+1,⋯,n时,0-1背包问题的最优解
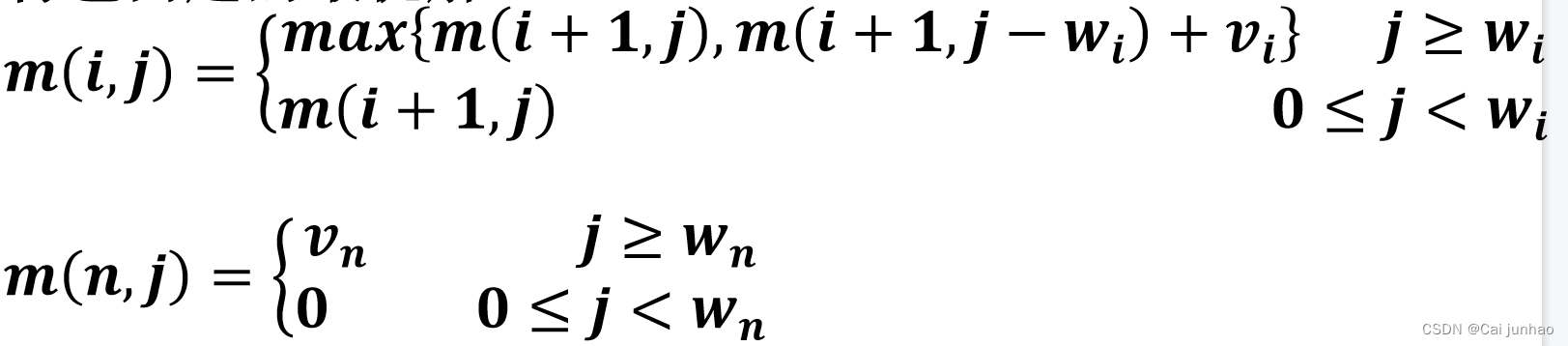
3.计算最优值
template <class Type>
void Knapsack(Type *v, int *w, int n, Type **m)
{int jMax=min(w[n]-1,c);//找<w[n]的临界值,并避免物品n比背包容量还要大的情况 //最小子问题,填写最后一行m[n][j] for(int j=0;j<=jMax;j++)m[n][j]=0;for(int j=w[n];j<=c;j++)m[n][j]=v[n];for(int i=n-1;i>1;i--){jMax=min(w[i]-1,c);for(int j=0;j<=jMax;j++)m[i][j]=m[i+1][j];//物品i装不进去for(int j=w[i];j<=c;j++)m[i][j]=max(m[i+1][j],m[i+1][j-w[i]]+v[i]);//能装但不装,装进去,两个值中取较大值 }//填最后一行 m[1][c]=m[2][c];//若物品1装不进去 if(c>=w[1])//若物品1可以装 m[1][c]=max(m[2][c],m[2][c-w[1]]+v[1]);
}
step1:实现递归出口,填矩阵m的第n行(前3行)step2:循环,实现递归式,填矩阵m的第(n−1)行到第2行step3:填m[1][c]
4.构造最优解
template <class Type>
void Traceback(Type **m, int *w, int c, int n, int *x)//m表已经填好,已知w、c、n,输出x[],0不装,1装入
{for(int i=1;i<n;i++){if(m[i][c]==m[i+1][c])x[i]=0;//相同则不装else{x[i]=1;c-=w[i];}}x[n]=(m[n][c])?1:0; }
第五章 回溯法
溯法有“通用的解题法”之称。
用它可以系统地搜索一个问题的所有解或任意解
它在问题的解空间树中,按深度优先策略,从根结点出发搜索解空间树。算法搜索至解空间树的任一结点时,先判断该结点是否包含问题的解。如果肯定不包含,则跳过对以该点为根的子树的搜索,逐层向其祖先结点回溯;否则进入该子树,继续按深度优先策略搜索。
问题的解空间
用回溯法解问题时,应明确定义问题的解空间。
指包含解的“集合”,结构常为树或者图。
问题的解空间至少应包含问题的一个(最优)解。
0-1背包
迭代回溯
有两种方案:
第一种是保存所有子集
第二种是添加剪枝函数
3个状态:左子树、右子树、回溯
在左、右子树添加约束函数、限界函数
两种剪枝函数:
约束函数:在扩展结点处剪去不满足约束的子树;
限界函数:剪去得不到最优解的子树。
0-1背包问题(树结构)
期末考点
1.熟练求出上界的n0,C,g(N)
2.清楚Ackerman函数的代码实现
3.熟练掌握大整数相乘的p,q,r;掌握其求解过程
4.清楚大整数乘法的代码实现,尤其是递归出口
5.掌握动态规划中0-1背包的代码实现、m表、s表、及其求最优值的解
6.在动态规划中0-1背包的代码中,可能会考察代码填空,变量的各阶段的值
7.掌握备忘录代码的具体实现
8.回溯法中的旅行售货员内容 及 整本书的定义内容不会考察。
掌握的意思是必考;清楚代表可能重点考察
期末在头歌上考,有代码填空及代码分析两种题型
相关文章:
【算法与设计】期末总结
文章目录 第一章 概述算法与程序时间复杂性求上界 第二章 递归与分治双递归函数——Ackerman函数分治策略大整数乘法两位两位四位x四位 三位x三位两位x六位 第三章 动态规划矩阵连乘基本要素最优子结构子问题重叠 备忘录 第四章 贪心算法活动安排问题基本要素贪心选择性质最优子…...

odoo报错KeyError: ‘ir.http‘
使用odoo17代码,python3.10.11配好的开发环境,当启动以后,浏览器登录访问的时候,后台报错 ERROR odoo_db odoo.modules.loading: Database odoo_db not initialized, you can force it with -i base File "/opt/odoo/odoo/o…...

每日的影视作品推荐❗❗
每日的影视作品推荐:剧名:《无法抗拒的男友们》主演:王子清、文苡帆 推荐理由:演技出色:王子清和文苡帆的演技非常出色,他们将角色间的情感变化演绎得细腻而真实,让人仿佛身临其境。 情感深刻&a…...
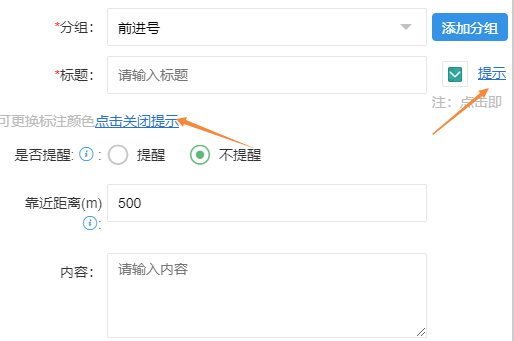
css 文字下划线 text-decoration
背景: 在某些时候需要给文字添加特殊样式。使用 text-decoration: underline; 来为段落文字添加下划线。也有其它文本装饰样式,例如: none:无装饰(去掉装饰)overline:上划线line-through&…...
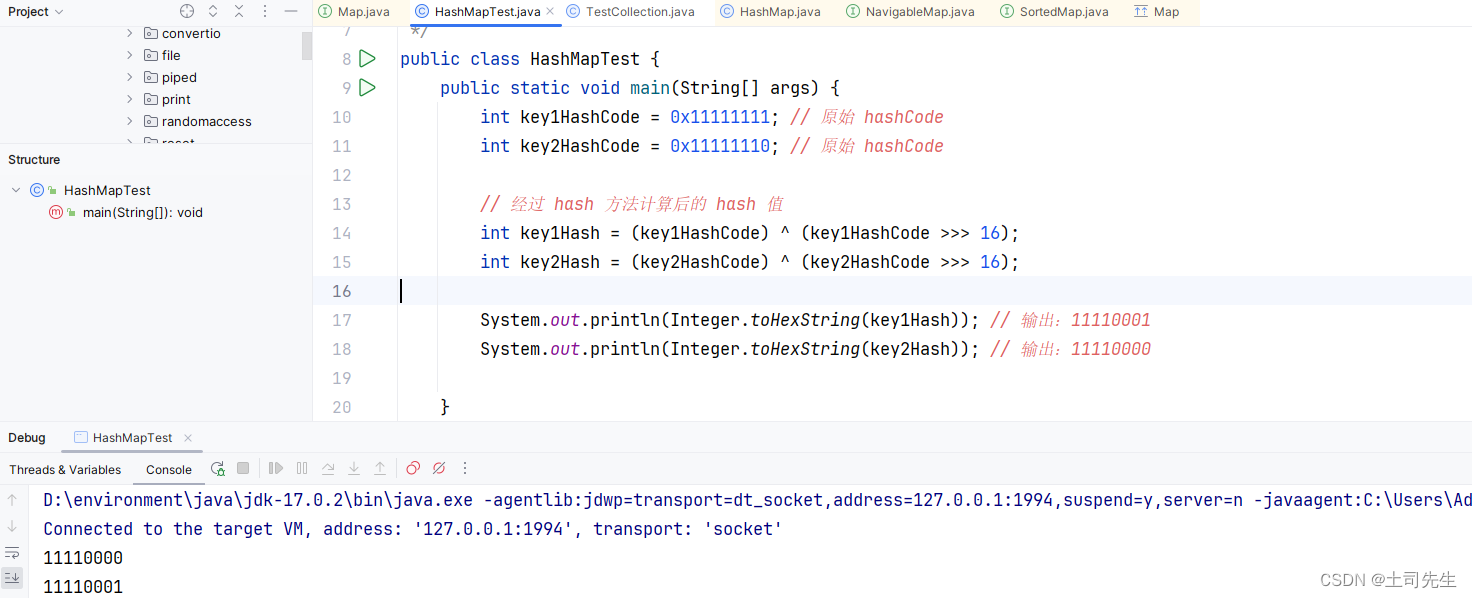
Java-01-基础篇-04 Java集合-04-HashMap (源码)
目录 一,HashMap 1.1 HashMap 属性分析 1.2 HashMap 构造器 1.3 HashMap 内置的 Node 类 1.4 HashMap 内置的 KeySet 类 1.5 HashMap 内置的 Values 类 1.6 HashMap 内置的 EntrySet 类 1.7 HashMap 内置的 UnsafeHolder 类 1.8 HashMap 相关的迭代器 1.9…...
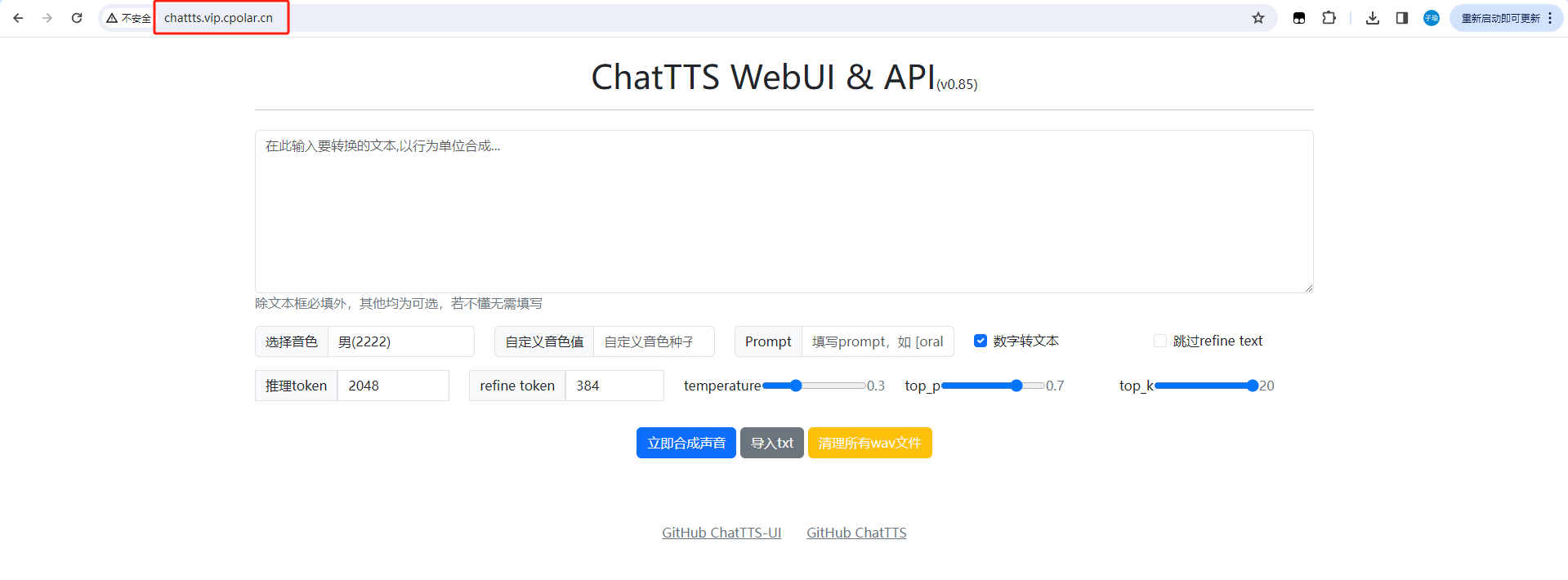
开源语音合成模型ChatTTS本地部署结合内网穿透实现远程访问
文章目录 前言1. 下载运行ChatTTS模型2. 安装Cpolar工具3. 实现公网访问4. 配置ChatTTS固定公网地址 前言 本篇文章就教大家如何快速地在Windows中本地部署ChatTTS,并且我们还可以结合Cpolar内网穿透实现公网随时随地访问ChatTTS AI语言模型。 最像人声的AI来了&a…...

超多细节—app图标拖动排序实现详解
前言: 最近做了个活动需求大致类似于一个拼图游戏,非常接近于咱们日常app拖动排序的场景。所以想着好好梳理一下,改造改造干脆在此基础上来写一篇实现app拖动排序的文章,跟大家分享下这个大家每天都要接触的场景,到底…...

基于深度学习的文字识别
基于深度学习的文字识别 基于深度学习的文字识别(Optical Character Recognition, OCR)是指利用深度神经网络模型自动识别和提取图像中的文字内容。这一技术在文档数字化、自动化办公、车牌识别、手写识别等多个领域有着广泛的应用。 深度学习OCR的基本…...
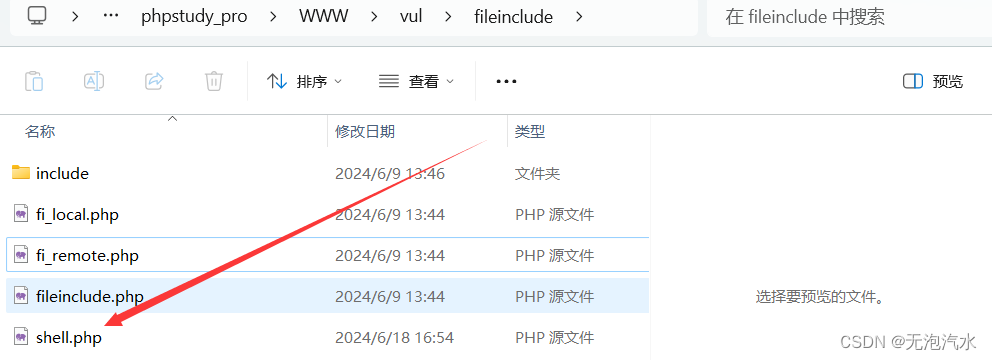
Pikachu靶场--文件包含
参考借鉴 Pikachu靶场之文件包含漏洞详解_pikachu文件包含-CSDN博客 文件包含(CTF教程,Web安全渗透入门)__bilibili File Inclusion(local) 查找废弃隐藏文件 随机选一个然后提交查询 URL中出现filenamefile2.php filename是file2.php&…...

get put post delete 区别以及幂等
GET 介绍:GET请求用于从服务器获取资源,通常用于获取数据。它的参数会附加在URL的末尾,可以通过URL参数传递数据。GET请求是幂等的,即多次请求同一个URL得到的结果应该是一样的,不会对服务器端产生影响。 特点…...

ultralytics版本及对应的更新
Ultralytics Ultralytics 是一家专注于计算机视觉和深度学习工具的公司,尤以其开源的 YOLO (You Only Look Once) 系列深受欢迎。目前,Ultralytics 主要管理和开发 YOLOv5 和 YOLOv8。以下是各个版本的概述及其主要更新: YOLOv5 YOLOv5 是…...
进行集成和协作?)
在现代编程环境中,Perl 如何与其他流行语言(如 Python、Java 等)进行集成和协作?
在现代编程环境中,Perl 可以与其他流行语言(如 Python、Java 等)进行集成和协作。以下是一些常见的方法: 调用外部程序:Perl 可以使用系统调用来执行其他语言编写的可执行文件。这意味着可以从 Perl 中调用 Python、Ja…...

BEV 中 multi-frame fusion 多侦融合(一)
文章目录 参数设置align_dynamic_thing:为了将动态物体的点云数据从上一帧对齐到当前帧流程旋转函数平移公式filter_points_in_ego:筛选出属于特定实例的点get_intermediate_frame_info: 函数用于获取中间帧的信息,包括点云数据、传感器校准信息、自车姿态、边界框及其对应…...

“Docker操作案例实践“
目录 1. 下载nginx 2. Portainer可视化 1. 下载nginx 步骤: 搜索nginx:docker search nginx;下载镜像:docker pull nginx ;查看镜像:docker images ;后台运行 :docker run -d -na…...
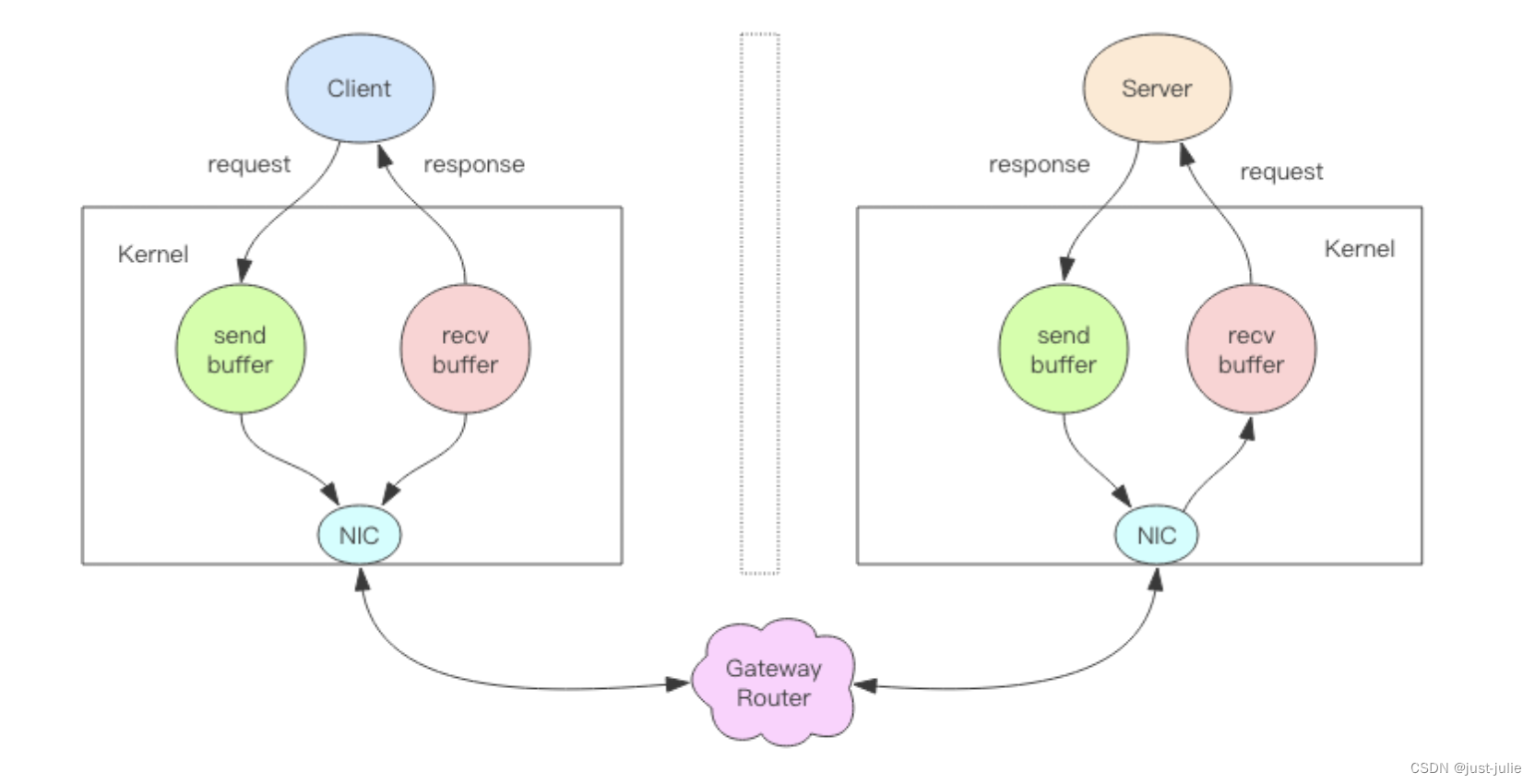
Redis 管道
Redis的消息交互 当我们使用客户端对Redis进行一次操作时,如下图所示,客户端将请求传送给服务器,服务器处理完毕后,再将响应回复给客户端,这要花费一个网络数据包来回的时间。 如果连续执行多条指令,那就会…...

ubuntu20.04安装配置openMVG+openMVS
安装 主要跟着官方教程逐步安装 openMVG https://github.com/openMVG/openMVG/blob/master/BUILD.md openMVS https://github.com/cdcseacave/openMVS/wiki/Building 注意事项 1. 库版本要求 使用版本: openMVS 2.2.0 openMVG Eigen 3.4.0 OpenCV 4.6.0 Ce…...

使用CSS常见问题解答卡片
常见问题解答卡片 效果展示 CSS 知识点 CSS 选择器的使用background 渐变背景色运用CSS 综合知识运用 页面整体布局 <div class"container"><h1>经常问的问题</h1><!-- 这里只是展示一个项目 --><div class"tab"><in…...

Kong AI Gateway 正式 GA !
Kong Gateway 3.7 版本已经重磅上线,我们给 AI Gateway 带来了一系列升级,下面是 AI Gateway 的更新亮点一览。 AI Gateway 正式 GA 在 Kong Gateway 的最新版本 3.7 中,我们正式宣布 Kong AI Gateway 达到了通用可用性(GA&…...
HTML5有哪些新特性?
目录 1.语义化标签:2.多媒体支持:3.增强型表单:4.绘图与图形:5.地理定位:6.离线应用与存储:7.性能与集成:8.语义化属性:9.改进的 DOM 操作:10.跨文档通信:11.…...
SQL Server入门-SSMS简单使用(2008R2版)-2
环境: win10,SQL Server 2008 R2 参考: SQL Server 管理套件(SSMS)_w3cschool https://www.w3cschool.cn/sqlserver/sqlserver-oe8928ks.html SQL Server存储过程_w3cschool https://www.w3cschool.cn/sqlserver/sql…...

KubeSphere 容器平台高可用:环境搭建与可视化操作指南
Linux_k8s篇 欢迎来到Linux的世界,看笔记好好学多敲多打,每个人都是大神! 题目:KubeSphere 容器平台高可用:环境搭建与可视化操作指南 版本号: 1.0,0 作者: 老王要学习 日期: 2025.06.05 适用环境: Ubuntu22 文档说…...

java_网络服务相关_gateway_nacos_feign区别联系
1. spring-cloud-starter-gateway 作用:作为微服务架构的网关,统一入口,处理所有外部请求。 核心能力: 路由转发(基于路径、服务名等)过滤器(鉴权、限流、日志、Header 处理)支持负…...

从WWDC看苹果产品发展的规律
WWDC 是苹果公司一年一度面向全球开发者的盛会,其主题演讲展现了苹果在产品设计、技术路线、用户体验和生态系统构建上的核心理念与演进脉络。我们借助 ChatGPT Deep Research 工具,对过去十年 WWDC 主题演讲内容进行了系统化分析,形成了这份…...

Vue3 + Element Plus + TypeScript中el-transfer穿梭框组件使用详解及示例
使用详解 Element Plus 的 el-transfer 组件是一个强大的穿梭框组件,常用于在两个集合之间进行数据转移,如权限分配、数据选择等场景。下面我将详细介绍其用法并提供一个完整示例。 核心特性与用法 基本属性 v-model:绑定右侧列表的值&…...

【Redis技术进阶之路】「原理分析系列开篇」分析客户端和服务端网络诵信交互实现(服务端执行命令请求的过程 - 初始化服务器)
服务端执行命令请求的过程 【专栏简介】【技术大纲】【专栏目标】【目标人群】1. Redis爱好者与社区成员2. 后端开发和系统架构师3. 计算机专业的本科生及研究生 初始化服务器1. 初始化服务器状态结构初始化RedisServer变量 2. 加载相关系统配置和用户配置参数定制化配置参数案…...

Opencv中的addweighted函数
一.addweighted函数作用 addweighted()是OpenCV库中用于图像处理的函数,主要功能是将两个输入图像(尺寸和类型相同)按照指定的权重进行加权叠加(图像融合),并添加一个标量值&#x…...

【SQL学习笔记1】增删改查+多表连接全解析(内附SQL免费在线练习工具)
可以使用Sqliteviz这个网站免费编写sql语句,它能够让用户直接在浏览器内练习SQL的语法,不需要安装任何软件。 链接如下: sqliteviz 注意: 在转写SQL语法时,关键字之间有一个特定的顺序,这个顺序会影响到…...

实现弹窗随键盘上移居中
实现弹窗随键盘上移的核心思路 在Android中,可以通过监听键盘的显示和隐藏事件,动态调整弹窗的位置。关键点在于获取键盘高度,并计算剩余屏幕空间以重新定位弹窗。 // 在Activity或Fragment中设置键盘监听 val rootView findViewById<V…...

Maven 概述、安装、配置、仓库、私服详解
目录 1、Maven 概述 1.1 Maven 的定义 1.2 Maven 解决的问题 1.3 Maven 的核心特性与优势 2、Maven 安装 2.1 下载 Maven 2.2 安装配置 Maven 2.3 测试安装 2.4 修改 Maven 本地仓库的默认路径 3、Maven 配置 3.1 配置本地仓库 3.2 配置 JDK 3.3 IDEA 配置本地 Ma…...

有限自动机到正规文法转换器v1.0
1 项目简介 这是一个功能强大的有限自动机(Finite Automaton, FA)到正规文法(Regular Grammar)转换器,它配备了一个直观且完整的图形用户界面,使用户能够轻松地进行操作和观察。该程序基于编译原理中的经典…...
