论文精读——KAN
目录
1.研究背景
2.关键技术
2.1 原始公式
2.2 KAN结构
2.3 缩放定律
3.技术扩展
4.模型效果
5.相关讨论
6.总结
文章标题:《KAN: Kolmogorov–Arnold Networks》
文章地址:
KAN: Kolmogorov-Arnold Networks (arxiv.org)![]() https://arxiv.org/abs/2404.19756代码地址:
https://arxiv.org/abs/2404.19756代码地址:
KindXiaoming/pykan: Kolmogorov Arnold Networks (github.com)![]() https://github.com/KindXiaoming/pykan
https://github.com/KindXiaoming/pykan
1.研究背景
MLP作为深度学习模型中的基础模块,有很好的非线性函数逼近能力,但是作者认为MLP并不是最好的非线性回归器。例如在Transformer中MLP消耗了几乎所有的非嵌入参数,并且可解释性较弱。因此,作者提出用KAN来替代MLP
KAN有以下特点:
①全连接结构
②边上的可学习激活函数
③权重参数被替换成可学习的样条函数
④在节点处进行简单的相加操作
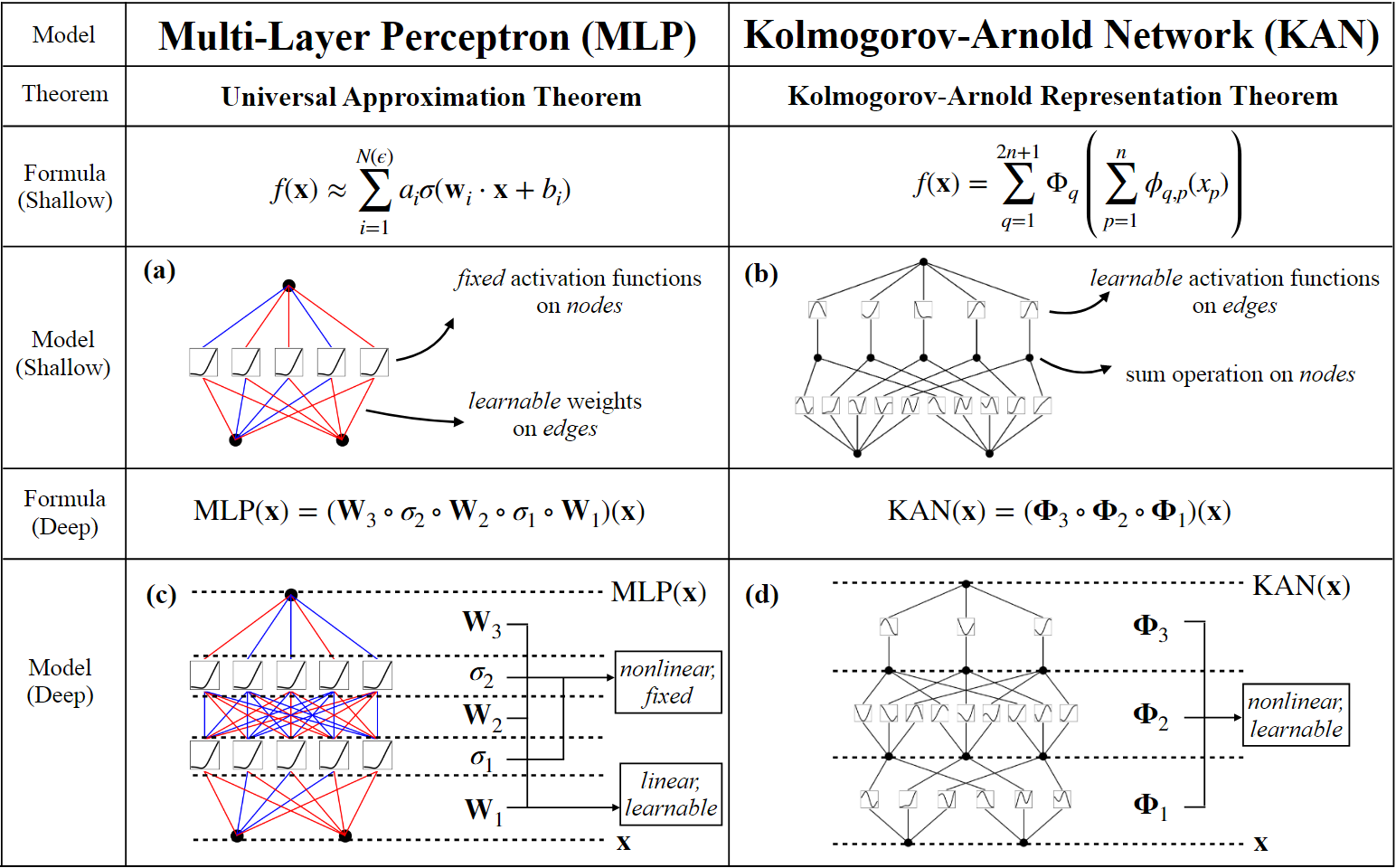
作者从理论上分析了为什么KAN有更好的效果:
其一,样条函数对于低维空间是精准,但是由于它不能利用复杂结构导致在高维的效果较差(维度灾难)
其二,由于MLP能够进行特征学习避免了维度灾难,但它无法优化单变量函数使得在低维空间不如样条函数 KAN利用了上述的两个结构,互相弥补了缺点

2.关键技术
2.1 原始公式
Kolmogorov-Arnold(KA) Representation Theorem假设是一个在有界域上的多元连续函数,那么
可以写成有限多个单变量连续函数相加
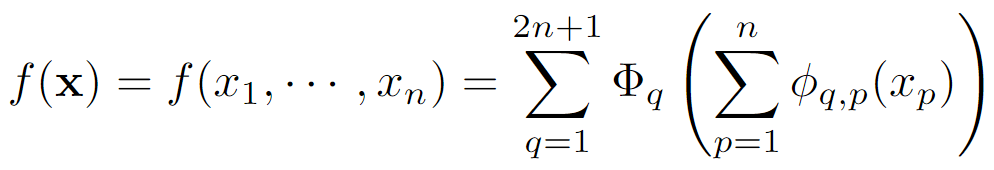
但是这个原始表达式只对应了一个拥有两层非线性激活函数,并且隐藏层只有2n+1个节点的网络

如果仅仅利用原表达式去做机器学习(拟合、回归等),由于一维函数可能非平滑,所以在实际操作中并非是可学习的
2.2 KAN结构
任务定义:找到函数,拟合输入输出对
,使得
,对应于原始公式只需要找到
和
即可
![]()
表示一维函数矩阵,定义q为输出维度,p为输入维度
定义KAN的形状表示为:
![]()
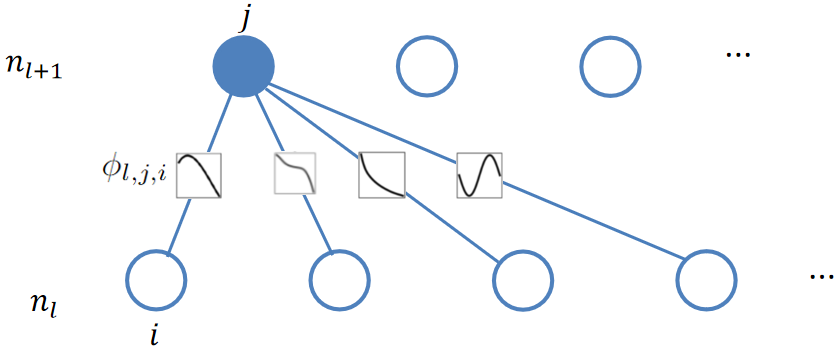
其中,ni表示第i层节点个数 定义第i个神经元在第l层表示为(l, i),表示(l, i)神经元的激活值,第l层和第l+1层之间有
个激活函数(因为激活函数在边上,并且为全连接),那么(l, i)和(l+1, i)之间的激活函数可以表示成
![]()
上述过程对应于下图:
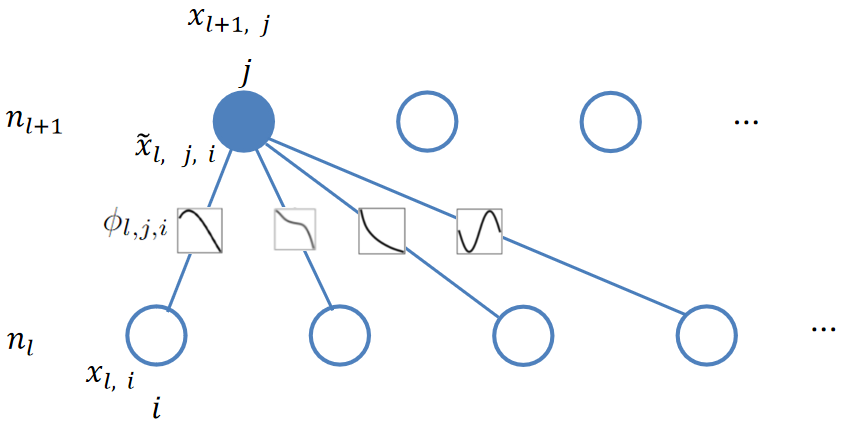
因此第l+1层的第j个节点可表示成:

写成矩阵形式为:

其中,表示第l层的激活函数矩阵,那么对应一个有L层的KAN网络,有:
![]()
写成与原始公式相似的形式:

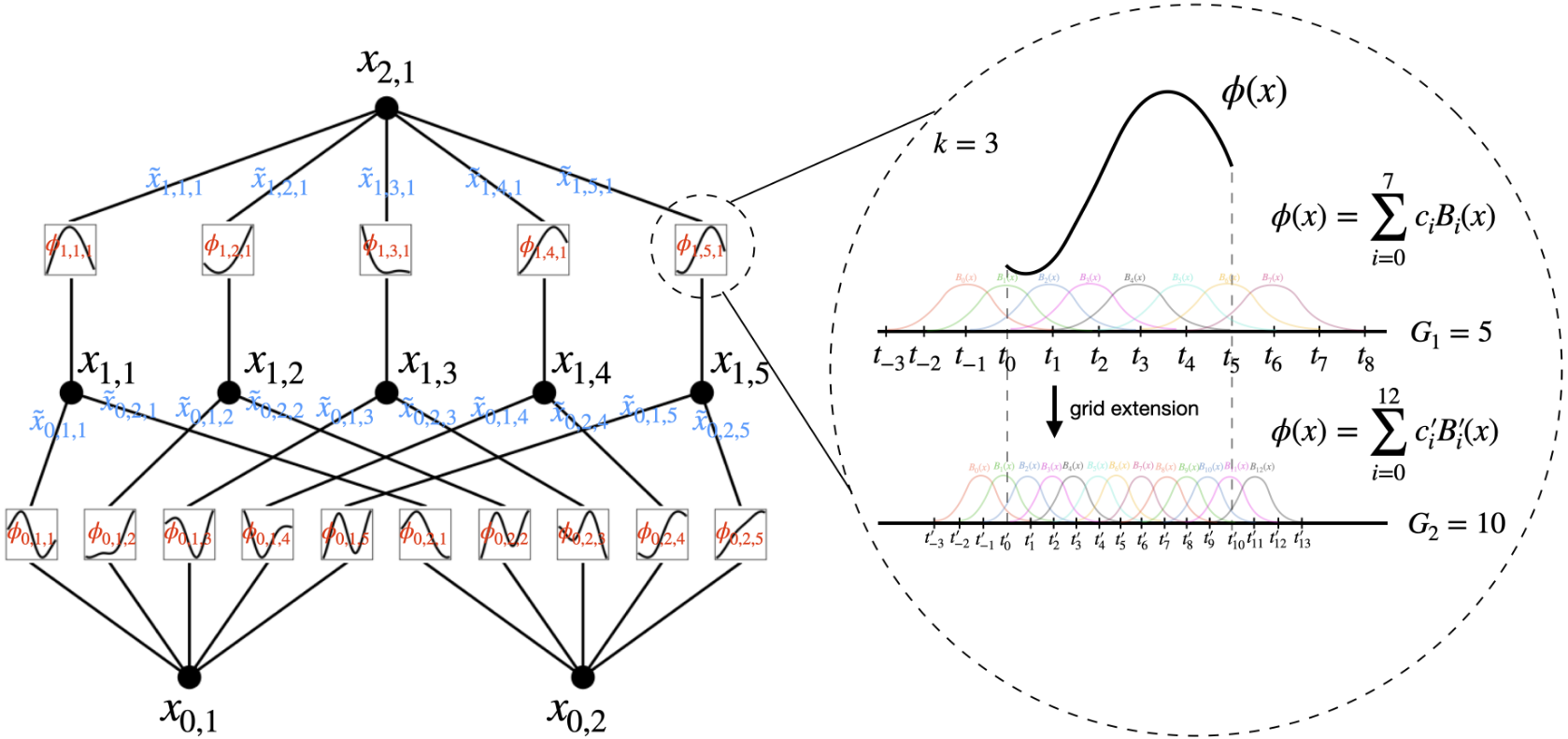
在实现上,激活函数采用多个一维的B-Spline函数的结合,并利用残差激活函数
![]()
![]()

参数量对比,L层,宽度N(k表示样条函数为k阶)
KAN:(上限挺好推的,但是下限不太懂为什么是+k而不是*k)
![]()
MLP:
![]()
2.3 缩放定律
神经缩放定律是测试损失(test Loss)随着模型参数的增加而减小的现象,即![]() 其中 ℓ 是测试 RMSE,N 是参数数量,α 是缩放指数。也就是说,参数量越大,误差越小(精度越高)
其中 ℓ 是测试 RMSE,N 是参数数量,α 是缩放指数。也就是说,参数量越大,误差越小(精度越高)
KAN能通过细分数据域网络来提高B-Spline函数逼近的精度,从而使缩放更加自由,能够有效控制参数量。而MLP对于不同的网格划分需要重新进行训练
例如,可以先训练一个参数较少的 KAN,然后通过使Spline网格粒度更细,使其扩展到参数较多的 KAN,这一方式降低了复杂度
3.技术扩展
为了提高KAN的可解释性,作者提出了一些简化模型的技术:
①稀疏化
MLP:L1正则化
KAN:定义L1范数,去除线性权重,再加上熵正则化
因此可以得到整体的训练损失为:
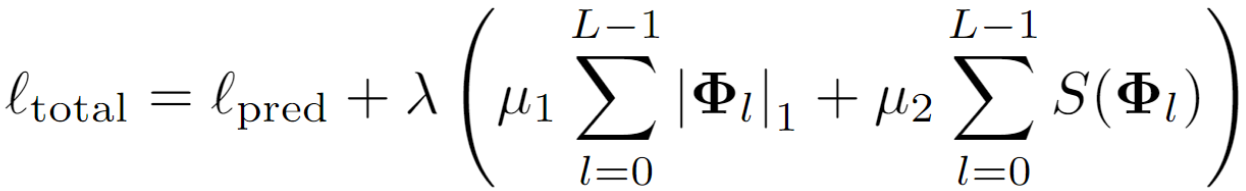
预测损失+L1正则化+熵正则化,通过λ控制正则化幅度
②可视化
将激活函数的透明度设置为与成正比,其中 β = 3
重要的函数会凸显出来
③剪枝
对每个节点定义输入输出分数,输入输出分数都大于阈值的节点会被保留下来,其余会被修剪掉
![]()
④符号化
如果猜测某些激活函数实际上是符号函数(例如 cos 或 log),则提供一个接口将其设置为指定的符号形式,后续只需要拟合参数即可

在剪枝完后,用户可以根据形状选择符号函数的公式,然后进一步训练,如果训练损失下降了,就表明选择了正确的符号表达式
4.模型效果
①拟合精度方面的比较
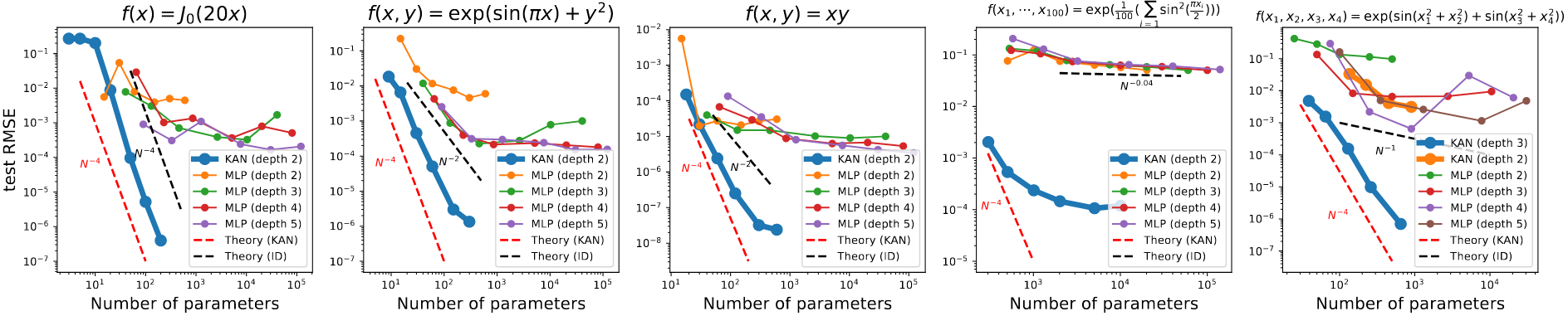
KAN有更好的放缩曲线,特别是高维,而MLP很快就饱和了,表明了KAN的扩展能力很强,并且KAN像MLP一样网络越深效果越好
②解决更复杂的偏微分方程

KAN 使用较小的网络和更少的参数实现了更好的误差缩放定律
作者还将KAN用在数学和物理领域的一些实际应用上,均表明KAN能用更少的参数量得到更好的效果
5.相关讨论
KAN还有一些可以改进的地方:
①在精度层面,还可以进一步研究模型结构和训练细节来提高效果
②对于KAN来说,最大的问题是训练太慢,因为无法利用batch计算,可以尝试对激活函数分组,同一组内使用相同的激活函数
③可以引入自适应性来提高KAN的精度和效率
④将KAN用在实际任务中,机器学习/理论科学
⑤由于KAN具有可解释性,可以尝试与AI4Science结合

6.总结
KAN基于Kolmogorov-Arnold Representation Theorem,并对两层网络进行扩展。通过将可学习激活函数设置在边上,而节点处进行简单的相加操作构建了KAN模型。由于KAN使用较少的参数量就能媲美MLP,并且还能通过简化技术使其具有良好的可解释性,因此KAN有望替代MLP作为神经网络中的基础模块。相比MLP而言,KAN有更好的缩放性能,但在相同的参数量下,KAN的训练速度过慢成为了最大的问题。
笔者的思考:
①作者强调了浅层的KAN就能达到甚至超过深层MLP的性能,是否意味着深层的KAN不太能实现(训练太慢,小模型适用)
②KAN不太适用于现在的深度学习框架,从硬件计算层面不太有优势
③从网络架构来看,其实KAN和MLP差不多(虽然原理不同),区别在于MLP是进行线性组合再进行激活,而KAN是先进行激活再线性组合,并且KAN中不同边上的激活函数并不相同,也正是这点带来了额外的计算复杂度,是否意味着KAN只是MLP更一般的形式
④笔者认为本文最大的特点是可解释性,适合用在较小的问题上,在AI4Science领域可能会有较大提高
相关文章:

论文精读——KAN
目录 1.研究背景 2.关键技术 2.1 原始公式 2.2 KAN结构 2.3 缩放定律 3.技术扩展 4.模型效果 5.相关讨论 6.总结 文章标题:《KAN: Kolmogorov–Arnold Networks》 文章地址: KAN: Kolmogorov-Arnold Networks (arxiv.org)https://arxiv.org/a…...
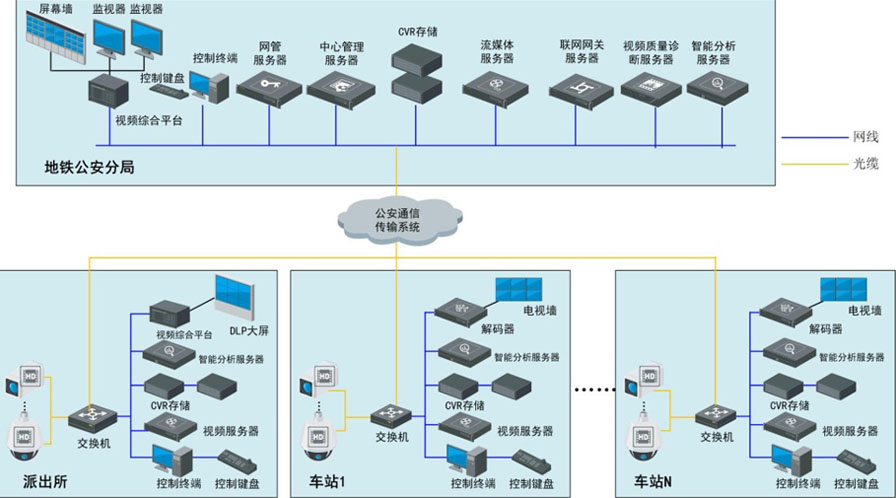
全国产城市轨道交通运营公安AI高清视频监控系统
方案简介 城市轨道交通运营公安高清视频监控系统解决方案针对运营部门和公安部门的安保需求,选用华维视讯的各类前端和视频编解码、控制产品,通过统一平台提供视频监控服务和智能应用,满足轨道交通运营业主客运组织和抢险指挥的需求ÿ…...

python连接mysql数据库、FastAPI、mysql-connector-python
方法工具一、FastAPI 建议使用fast api中的pymysql pip3 install fastapi pip3 install pydantic pip3 install "uvicorn[standard]" pip3 中的3是 Python 3 版本的包管理器命令,用于安装和管理 Python 3 版本的第三方库。在某些系统中,同时…...

【idea】解决springboot项目中遇到的问题
一、Maven报错Could not find artifact com.mysql:mysql-connector-j:pom:unknown in aliyunmaven解决及分析 报错 创建springboot项目,勾选数据库驱动,springboot版本为3,现在改成了2.7.2,Maven就发生了报错Could not find art…...

ubuntu22.04禁止自动休眠的几种方式
在Ubuntu 20.04中,您可以通过以下几种方式禁用自动休眠功能: 使用systemd设置: sudo systemctl mask sleep.target suspend.target hibernate.target hybrid-sleep.target 修改/etc/systemd/logind.conf文件: sudo nano /etc/systemd/logind.conf 找…...
智能网站管理系统
智能网站管理系统,即智能化的网站管理工具,是为了提高网站管理效率和简化操作流程而开发的一种软件系统。它集合了各种先进的技术和功能,为网站管理员提供了一套强大而可靠的解决方案。 智能网站管理系统的核心功能是网站内容管理。传统的网站…...

Android Service学习笔记
1、Service介绍 Android Service(服务)是 Android 四大组件之一,主要作用是执行后台操作。它是一个后台运行的组件,执行长时间运行且不需要用户交互的任务。即使应用被销毁也依然可以工作。 Service并不是运行在一个独立的进程当…...
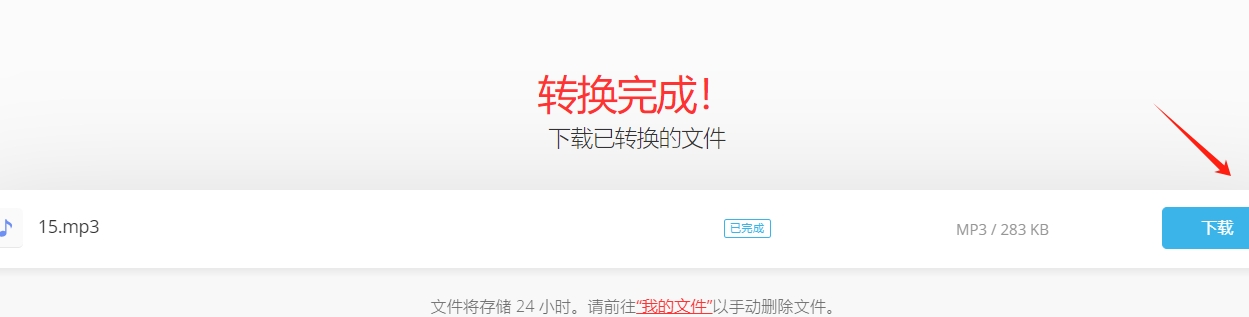
amr文件怎么转换成mp3?超好用的四种转换方法介绍!
amr文件怎么转换成mp3?在当今数字化时代,音频格式的多样性给我们带来了更广泛的选择,其中AMR格式就是其中之一,AMR格式在录音和通话领域得到广泛应用,但与此同时,它也存在一些挑战和局限性,尽管…...

翻转数位00
题目链接 翻转数位 题目描述 注意点 可以将一个数位从0变为1找出能够获得的最长的一串1的长度(必须是连续的) 解答思路 参照题解使用动态规划解决本题,对于任意一个位置i,dp[i][0]表示到达且包含第i位不翻转0最长1的长度&…...
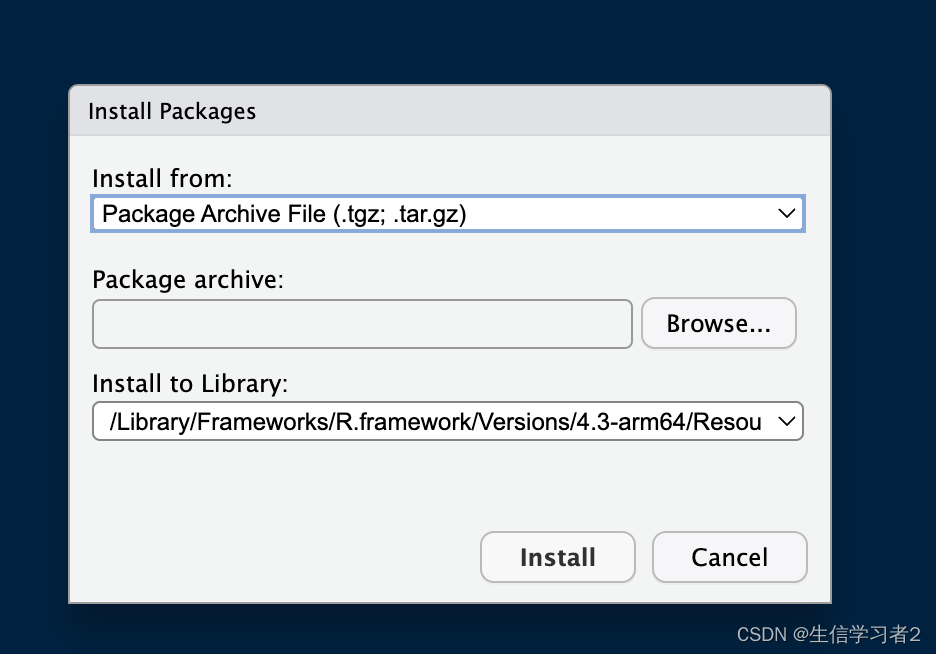
工具:安装R语言的R包的各种方法
欢迎大家关注全网生信学习者系列: WX公zhong号:生信学习者Xiao hong书:生信学习者知hu:生信学习者CDSN:生信学习者2 介绍 R语言提供的大量R包为众多研究者提供了足够的工具,但是如何安装R包是很多人在使…...
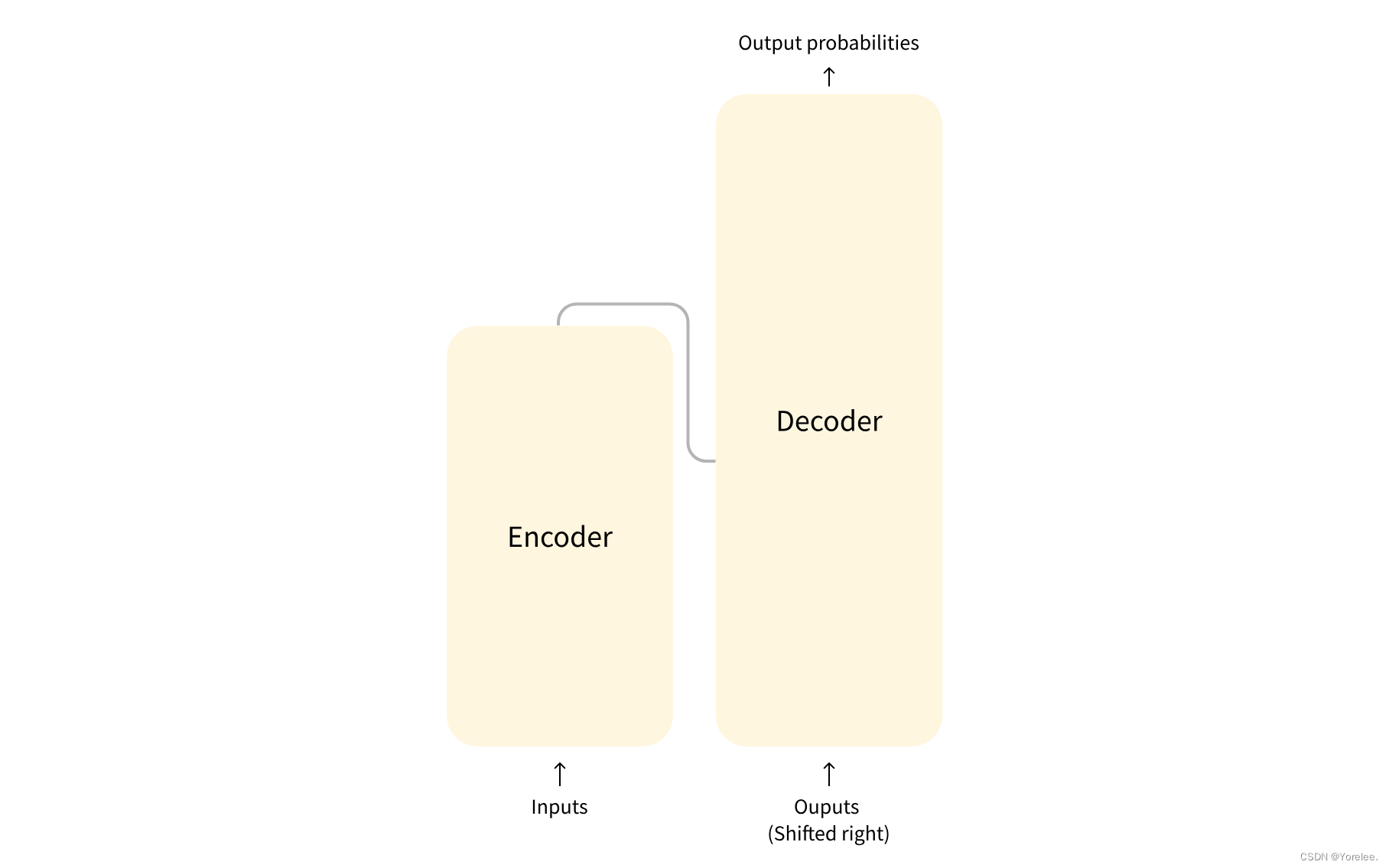
注意力机制和Transformer模型各部分功能解释
文章目录 Transformer1、各部分功能解释2、通过例子解释a.输入预处理位置编码b.Encoder 的处理c.Decoder的输入Decoder的工作流程d.输出预测总结 Attention代码和原理理解 Transformer 运行机理: (1)假设我们需要进行文本生成任务。我们将已…...

短路是怎么形成的
1. 短路分为电源短路和用电器短路。 电源短路:电流不经过任何用电器,直接由正极经过导线流向负极,由于电源内阻很小,导致短路电流很大,特别容易烧坏电源。 用电器短路:也叫部分电路短路,即一根…...
)
【ZZULIOJ】1106: 回文数(函数专题)
题目描述 一个正整数,如果从左向 右读(称之为正序数)和从右向左读(称之为倒序数)是一样的,这样的数就叫回文数。输入两个整数m和n(m<n),输出区间[m,n]之间的回文数。…...

数据库设计规范总结
数据库设计规范总结 大家好,我是免费搭建查券返利机器人省钱赚佣金就用微赚淘客系统3.0的小编,也是冬天不穿秋裤,天冷也要风度的程序猿! 数据库设计规范是指在设计数据库时应该遵循的一系列规则和标准,旨在提高数据库…...

深度学习(九)——神经网络:最大池化的作用
一、 torch.nn中Pool layers的介绍 官网链接: https://pytorch.org/docs/stable/nn.html#pooling-layers 1. nn.MaxPool2d介绍 nn.MaxPool2d是在进行图像处理时,Pool layers最常用的函数 官方文档:MaxPool2d — PyTorch 2.0 documentation &…...

「前端+鸿蒙」鸿蒙应用开发-ArkTS语法说明-组件声明
ArkTS 是鸿蒙应用开发中的一个框架,它允许开发者使用 TypeScript 语法来创建声明式的用户界面。在 ArkTS 中,组件声明是构建 UI 的基础。以下是 ArkTS 快速入门的指南,包括组件声明的语法说明和示例代码。 ArkTS 快速入门 - 语法说明 - 组件声明 组件基础 在 ArkTS 中,组…...

python的subprocess 模块
subprocess 模块是 2.4 版本中新增的模块, 它允许您生成新进程,连接到它们的 输入 / 输出 / 错误 管道,并获得它们的返回码 (状态信息), 该模块的目的在于取代几个较旧的模块和功能 subprocess 模块可以用于执行系统命令, 拿到执行的结果, 速度比较的快…...

【Arc gis】使用DEM提取流域范围
地址:arcgis DEM 提取流域范围(详细教程)(空间分析--Hydrology)_gis的gridcode是什么意思-CSDN博客...

大模型技术工程师:抓住时代机遇,成为行业精英_
伴随AI大模型的火热,中国科技大厂们正在掀起一场「跑步AI化」的风暴。从顶层战略到业务线重构,AI无疑已成为大厂们押注未来的新故事。 大模型时代已经到来 大模型已成为全球竞争热点,一个大模型时代已经到来。 大模型具备三个特点…...

孟德尔随机化R包:TwoSampleMR和MR-PRESSO安装
1. 孟德尔随机化R包 看一篇文章,介绍孟德尔随机化分析,里面推荐了这两个R包,安装了解一下: Methods:Genome-wide association study (GWAS) data for autoimmune diseases and AMD were obtained from the IEU Open GWAS databas…...

React 第五十五节 Router 中 useAsyncError的使用详解
前言 useAsyncError 是 React Router v6.4 引入的一个钩子,用于处理异步操作(如数据加载)中的错误。下面我将详细解释其用途并提供代码示例。 一、useAsyncError 用途 处理异步错误:捕获在 loader 或 action 中发生的异步错误替…...

OpenLayers 可视化之热力图
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 热力图(Heatmap)又叫热点图,是一种通过特殊高亮显示事物密度分布、变化趋势的数据可视化技术。采用颜色的深浅来显示…...

JavaScript 中的 ES|QL:利用 Apache Arrow 工具
作者:来自 Elastic Jeffrey Rengifo 学习如何将 ES|QL 与 JavaScript 的 Apache Arrow 客户端工具一起使用。 想获得 Elastic 认证吗?了解下一期 Elasticsearch Engineer 培训的时间吧! Elasticsearch 拥有众多新功能,助你为自己…...

通过Wrangler CLI在worker中创建数据库和表
官方使用文档:Getting started Cloudflare D1 docs 创建数据库 在命令行中执行完成之后,会在本地和远程创建数据库: npx wranglerlatest d1 create prod-d1-tutorial 在cf中就可以看到数据库: 现在,您的Cloudfla…...

全志A40i android7.1 调试信息打印串口由uart0改为uart3
一,概述 1. 目的 将调试信息打印串口由uart0改为uart3。 2. 版本信息 Uboot版本:2014.07; Kernel版本:Linux-3.10; 二,Uboot 1. sys_config.fex改动 使能uart3(TX:PH00 RX:PH01),并让boo…...

【VLNs篇】07:NavRL—在动态环境中学习安全飞行
项目内容论文标题NavRL: 在动态环境中学习安全飞行 (NavRL: Learning Safe Flight in Dynamic Environments)核心问题解决无人机在包含静态和动态障碍物的复杂环境中进行安全、高效自主导航的挑战,克服传统方法和现有强化学习方法的局限性。核心算法基于近端策略优化…...

【JVM】Java虚拟机(二)——垃圾回收
目录 一、如何判断对象可以回收 (一)引用计数法 (二)可达性分析算法 二、垃圾回收算法 (一)标记清除 (二)标记整理 (三)复制 (四ÿ…...

MySQL:分区的基本使用
目录 一、什么是分区二、有什么作用三、分类四、创建分区五、删除分区 一、什么是分区 MySQL 分区(Partitioning)是一种将单张表的数据逻辑上拆分成多个物理部分的技术。这些物理部分(分区)可以独立存储、管理和优化,…...

stm32wle5 lpuart DMA数据不接收
配置波特率9600时,需要使用外部低速晶振...

Windows电脑能装鸿蒙吗_Windows电脑体验鸿蒙电脑操作系统教程
鸿蒙电脑版操作系统来了,很多小伙伴想体验鸿蒙电脑版操作系统,可惜,鸿蒙系统并不支持你正在使用的传统的电脑来安装。不过可以通过可以使用华为官方提供的虚拟机,来体验大家心心念念的鸿蒙系统啦!注意:虚拟…...
