【专项】112. 路径总和
112. 路径总和
给你二叉树的根节点 root 和一个表示目标和的整数 targetSum 。判断该树中是否存在 根节点到叶子节点 的路径,这条路径上所有节点值相加等于目标和 targetSum 。如果存在,返回 true ;否则,返回 false 。
叶子节点 是指没有子节点的节点。
示例 1:
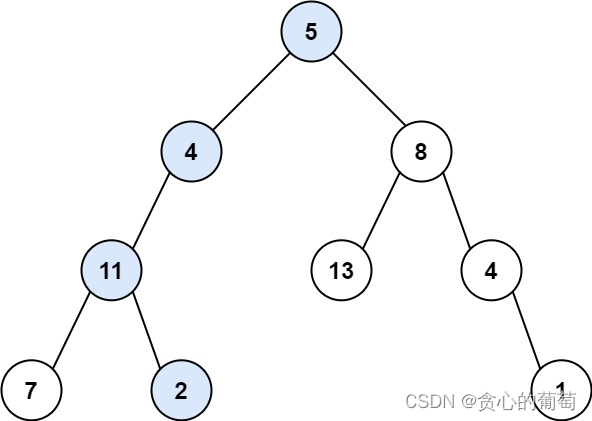
输入:root = [5,4,8,11,null,13,4,7,2,null,null,null,1], targetSum = 22
输出:true
解释:等于目标和的根节点到叶节点路径如上图所示。
示例 2:
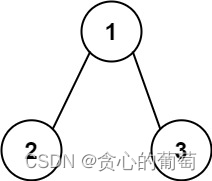
输入:root = [1,2,3], targetSum = 5
输出:false
解释:树中存在两条根节点到叶子节点的路径:
(1 --> 2): 和为 3
(1 --> 3): 和为 4
不存在 sum = 5 的根节点到叶子节点的路径。
示例 3:
输入:root = [], targetSum = 0
输出:false
解释:由于树是空的,所以不存在根节点到叶子节点的路径。
提示:
树中节点的数目在范围 [0, 5000] 内
-1000 <= Node.val <= 1000
-1000 <= targetSum <= 1000
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullptr), right(nullptr) {}* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:bool hasPathSum(TreeNode* root, int targetSum) {if (root == nullptr)return false;if (root->left == nullptr && root->right == nullptr)return targetSum == root->val;return hasPathSum(root->left, targetSum - root->val) || hasPathSum(root->right, targetSum - root->val);}
};
相关文章:

【专项】112. 路径总和
112. 路径总和 给你二叉树的根节点 root 和一个表示目标和的整数 targetSum 。判断该树中是否存在 根节点到叶子节点 的路径,这条路径上所有节点值相加等于目标和 targetSum 。如果存在,返回 true ;否则,返回 false 。 叶子节点 …...
【数据结构】堆排序
堆是一种叫做完全二叉树的数据结构,可以分为大根堆,小根堆,而堆排序就是基于这种结构而产生的一种程序算法。大堆:每个节点的值都大于或者等于他的左右孩子节点的值小堆:每个结点的值都小于或等于其左孩子和右孩子结点…...
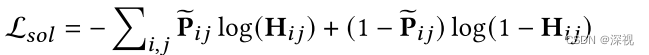
论文阅读笔记《GAMnet: Robust Feature Matching via Graph Adversarial-Matching Network》
核心思想 本文提出一种基于图对抗神经网络的图匹配算法(GAMnet),使用图神经网络作为生成器分别生成源图和目标图的节点的特征,并用一个多层感知机作为辨别器来区分两个特征是否来自同一个图,通过对抗训练的办法提高生成器特征提取…...

数据安全—数据完整性校验
1、数据安全保障三要素即 保密性 完整性、可用性机密性:要求数据不被他人轻易获取,需要进行数据加密。完整性:要求数据不被他人随意修改,需要进行签名技术可用性:要求服务不被他人恶意攻击,需要进行数据校验…...
Java 最小路径和
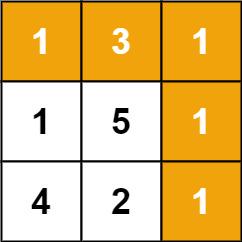
最小路径和中等给定一个包含非负整数的 m x n 网格 grid ,请找出一条从左上角到右下角的路径,使得路径上的数字总和为最小。说明:每次只能向下或者向右移动一步。示例 1:输入:grid [[1,3,1],[1,5,1],[4,2,1]]输出&…...
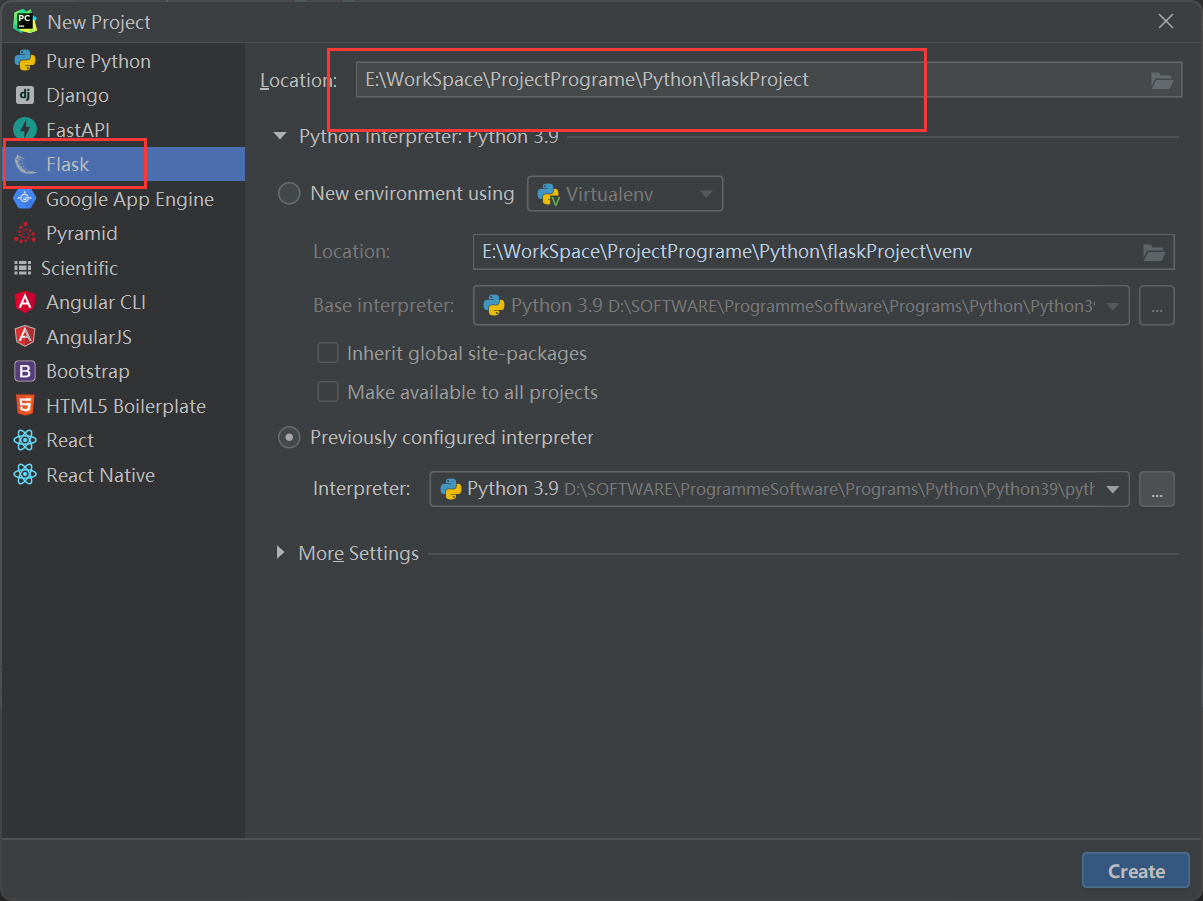
Flask+VUE前后端分离的登入注册系统实现
首先Pycharm创建一个Flask项目: Flask连接数据库需要下载的包: pip install -U flask-cors pip install flask-sqlalchemy Flask 连接和操作Mysql数据库 - 王滚滚啊 - 博客园 (cnblogs.com) sqlAlchemy基本使用 - 简书 (jianshu.com) FlaskVue前后端分…...
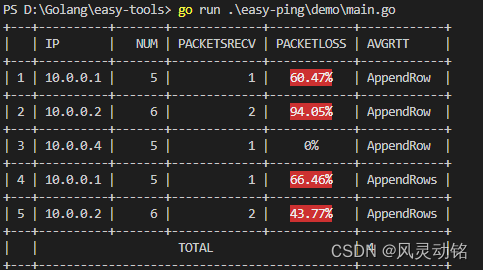
【Go】用Go在命令行输出好看的表格
用Go在命令行输出好看的表格前言正文生成Table表头设置插入行表格标题自动标号单元格合并列合并行合并样式设置居中设置数字自动高亮标红完整Demo代码结语前言 最近在写一些运维小工具,比如批量进行ping包的工具,实现不困难,反正就是ping&am…...

怎么处理消息重发的问题?
消息队列在消息传递的过程中,如果出现传递失败的情况,发送方会重试,在重试的过程中,可能会产生重复的消息。 消息重复的情况必然存在 关于传递消息时能够提供的服务质量标准,MQTT协议给出了三种不同的标准࿱…...
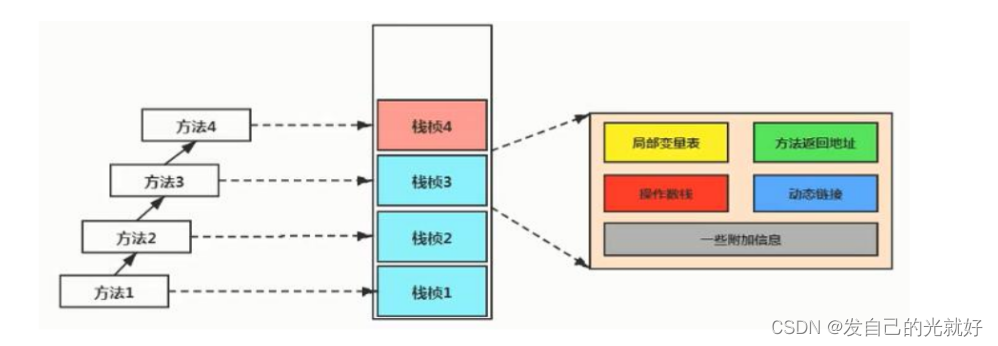
JVM 运行时数据区(数据区组成表述,程序计数器,java虚拟机栈,本地方法栈)
JVM 运行时数据区JVM 运行时数据区3.1运行时的数据区组成概述3.1.1程度计数器3.1.2java虚拟机栈3.1.3本地方法栈3.1.4java堆3.1.5方法区3.2程序计数器3.3java虚拟机栈3.4本地方法栈JVM 运行时数据区 堆,方法区(元空间) 主要用来存放数据 是线程共享的. 程序计数器,本地方法栈…...

Oracle ASM磁盘组配置、日常运维、故障处理等操作资料汇总
ASM(自动存储管理)在数据库中是非常重要的组成部分,它可以为磁盘提供统一的存储管理、提高磁盘访问的性能和可用性、简化管理复杂度,从而为数据库的运行提供更好的支持。这里就为大家整理了墨天轮数据社区上一些ASM相关基础知识、…...
java对象的创建与内存分配机制
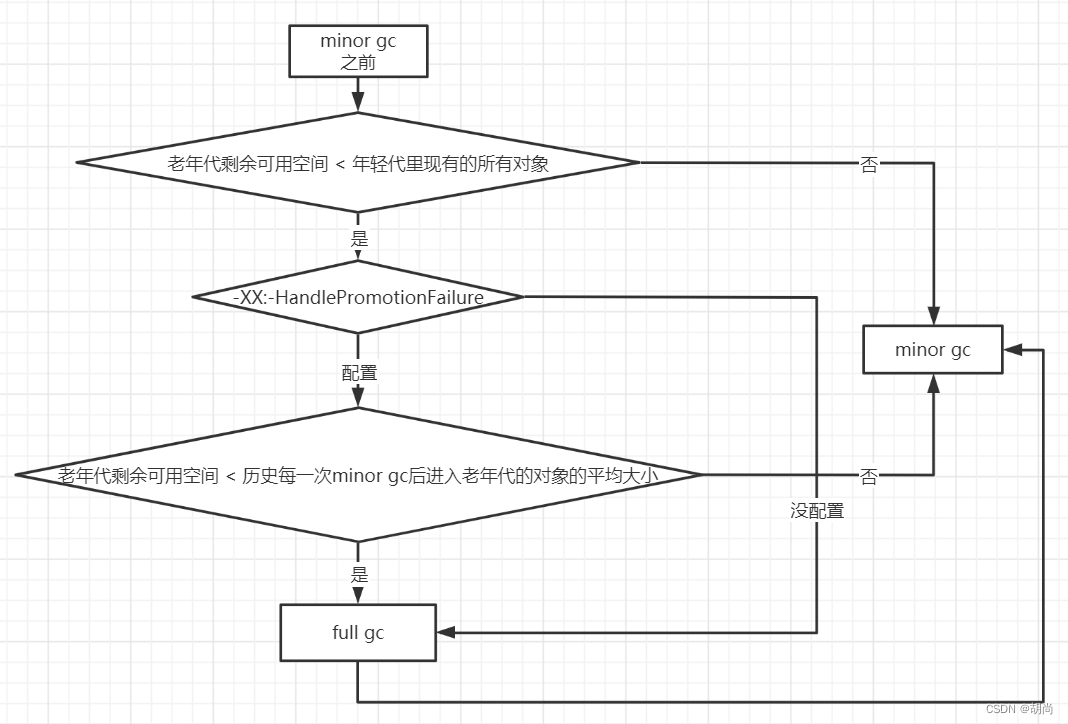
文章目录对象的创建与内存分配机制对象的创建类加载检查分配内存初始化零值设置对象头指向init方法其他:指针压缩对象内存分配对象在栈上分配对象在Eden区中分配大对象直接分配到老年代长期存活的对象进入老年代对象动态年龄判断老年代空间分配担保机制对象的内存回…...
本地存储localStorage、sessionStorage
目录 一、localStorage 二、sessionStorage 三、本地存储处理复杂数据 一、localStorage 介绍 (1)数据存储在用户浏览器中 (2)设置、读取方便、甚至页面刷新不会丢失数据 (3)容量较大,se…...

JavaSE: 网络编程
1.1 概述java程序员面对统一的网络编程环境B/S 架构 和 C/S架构1.2 网络通信的两个要素通信双方的地址:ip 端口号网络通信协议:TCP/IP协议(事实上的国际规则)、OSI模型(理想化)1.3 Inet Address本地回环地…...

计算机图形学09:二维观察之点的裁剪
作者:非妃是公主 专栏:《计算机图形学》 博客地址:https://blog.csdn.net/myf_666 个性签:顺境不惰,逆境不馁,以心制境,万事可成。——曾国藩 文章目录专栏推荐专栏系列文章序一、二维观察基本…...

2023Java 并发编程面试题
Java 并发编程 1、在 java 中守护线程和本地线程区别? java 中的线程分为两种:守护线程(Daemon)和用户线程(User)。任何线程都可以设置为守护线程和用户线程,通过方法Thread.setDaemon(boolon…...
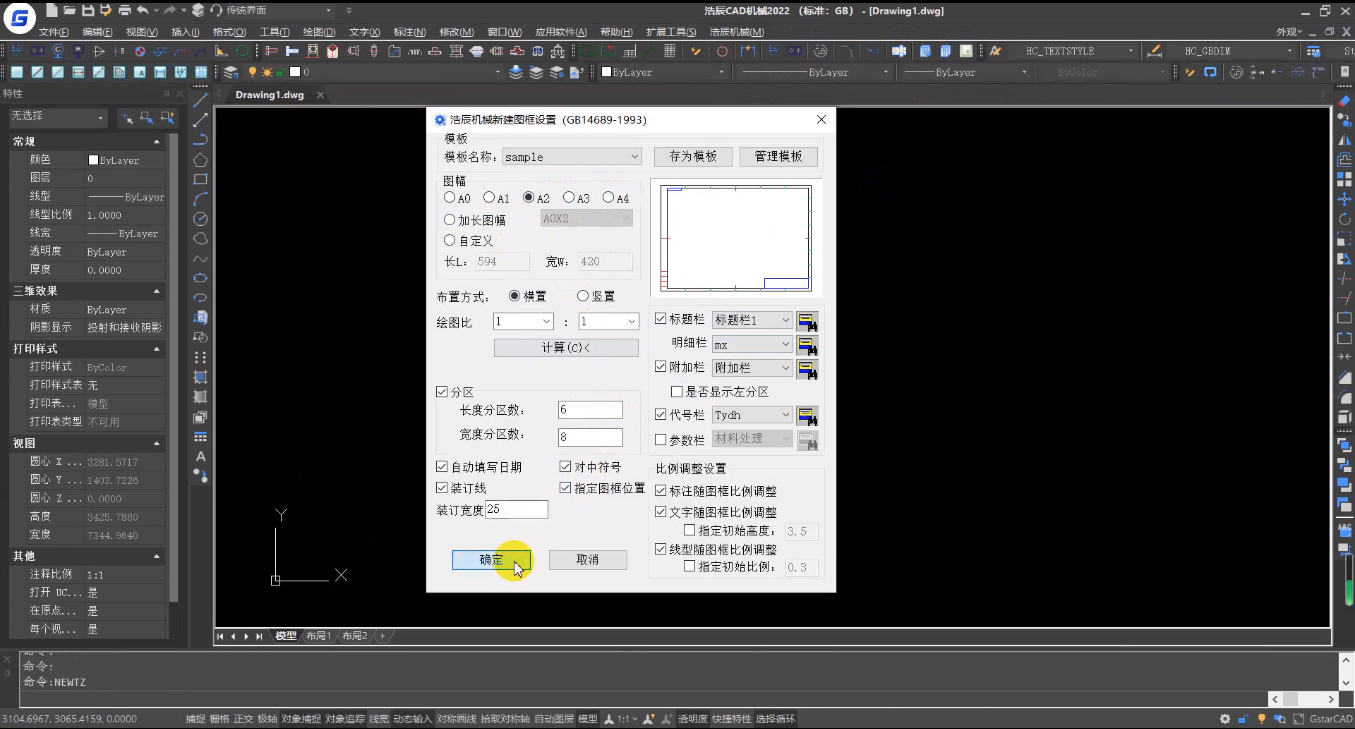
CAD如何绘制A0/A1/A2/A3/A4图框?
在CAD制图时,设计师一般会使用企业的定制图框模板或者个人的特色图框模板,让设计方案更加标准化、规范化。对于新人设计师而言,完成CAD制图已经非常头疼了,图框的绘制更是手忙脚乱。那么是否有更加高效的方式来完成A0、A1、A2、A3…...

R 安装 “umap-learn“ python 包
首先需要在R中下载并读取reticulate包,该包提供了一系列R-Python的交互式命令由于之前在电脑中通过三个方式安装了Python:直接安装 Python 3.10安装Anaconda,携带3.9安装 Miniconda,又是另外一个版本的Python版本各不相同…...

测试同学如何快速开发测试平台?
转眼已经好几个月没有发表什么文章了,因为疫情原因,大家工作都不怎么顺利,没有什么心情。再者,最近一直在搞移动端精准测试的项目,有太多技术难点需要攻克。从各个网站上都找不到解决方案,只能不断地尝试&a…...

【程序员接口百宝箱】免费常用API接口
一、短信发送 短信的应用可以说是非常的广泛了,短信API也是当下非常热门的API~ 短信验证码:可用于登录、注册、找回密码、支付认证等等应用场景。支持三大运营商,3秒可达,99.99%到达率,支持大容量高并发。…...

使数组和能被P整除[同余定理+同余定理变形]
同余定理同余定理变形前言一、使数组和能被P整除二、同余定理变形总结参考资料前言 同余定理非常经典,采用前缀和 map,当两个余数前缀和为一个值时,则中间一段子数组刚好对P整除。但是能否找到前面是否有一段子数组和可以对P整除呐…...

华为云AI开发平台ModelArts
华为云ModelArts:重塑AI开发流程的“智能引擎”与“创新加速器”! 在人工智能浪潮席卷全球的2025年,企业拥抱AI的意愿空前高涨,但技术门槛高、流程复杂、资源投入巨大的现实,却让许多创新构想止步于实验室。数据科学家…...

conda相比python好处
Conda 作为 Python 的环境和包管理工具,相比原生 Python 生态(如 pip 虚拟环境)有许多独特优势,尤其在多项目管理、依赖处理和跨平台兼容性等方面表现更优。以下是 Conda 的核心好处: 一、一站式环境管理:…...

【HarmonyOS 5.0】DevEco Testing:鸿蒙应用质量保障的终极武器
——全方位测试解决方案与代码实战 一、工具定位与核心能力 DevEco Testing是HarmonyOS官方推出的一体化测试平台,覆盖应用全生命周期测试需求,主要提供五大核心能力: 测试类型检测目标关键指标功能体验基…...

《从零掌握MIPI CSI-2: 协议精解与FPGA摄像头开发实战》-- CSI-2 协议详细解析 (一)
CSI-2 协议详细解析 (一) 1. CSI-2层定义(CSI-2 Layer Definitions) 分层结构 :CSI-2协议分为6层: 物理层(PHY Layer) : 定义电气特性、时钟机制和传输介质(导线&#…...

STM32F4基本定时器使用和原理详解
STM32F4基本定时器使用和原理详解 前言如何确定定时器挂载在哪条时钟线上配置及使用方法参数配置PrescalerCounter ModeCounter Periodauto-reload preloadTrigger Event Selection 中断配置生成的代码及使用方法初始化代码基本定时器触发DCA或者ADC的代码讲解中断代码定时启动…...

Qwen3-Embedding-0.6B深度解析:多语言语义检索的轻量级利器
第一章 引言:语义表示的新时代挑战与Qwen3的破局之路 1.1 文本嵌入的核心价值与技术演进 在人工智能领域,文本嵌入技术如同连接自然语言与机器理解的“神经突触”——它将人类语言转化为计算机可计算的语义向量,支撑着搜索引擎、推荐系统、…...

【碎碎念】宝可梦 Mesh GO : 基于MESH网络的口袋妖怪 宝可梦GO游戏自组网系统
目录 游戏说明《宝可梦 Mesh GO》 —— 局域宝可梦探索Pokmon GO 类游戏核心理念应用场景Mesh 特性 宝可梦玩法融合设计游戏构想要素1. 地图探索(基于物理空间 广播范围)2. 野生宝可梦生成与广播3. 对战系统4. 道具与通信5. 延伸玩法 安全性设计 技术选…...

代理篇12|深入理解 Vite中的Proxy接口代理配置
在前端开发中,常常会遇到 跨域请求接口 的情况。为了解决这个问题,Vite 和 Webpack 都提供了 proxy 代理功能,用于将本地开发请求转发到后端服务器。 什么是代理(proxy)? 代理是在开发过程中,前端项目通过开发服务器,将指定的请求“转发”到真实的后端服务器,从而绕…...

【Java学习笔记】BigInteger 和 BigDecimal 类
BigInteger 和 BigDecimal 类 二者共有的常见方法 方法功能add加subtract减multiply乘divide除 注意点:传参类型必须是类对象 一、BigInteger 1. 作用:适合保存比较大的整型数 2. 使用说明 创建BigInteger对象 传入字符串 3. 代码示例 import j…...

vulnyx Blogger writeup
信息收集 arp-scan nmap 获取userFlag 上web看看 一个默认的页面,gobuster扫一下目录 可以看到扫出的目录中得到了一个有价值的目录/wordpress,说明目标所使用的cms是wordpress,访问http://192.168.43.213/wordpress/然后查看源码能看到 这…...
