【算法——动态规划(从dfs回溯开始推导dp)】
基础理论
递归:
递:大问题分解子问题的过程 ; 归:产生答案
dp:只进行归;用已知的最底层的(递归的边界,搜索树的底),推出未知
《视频索引》
一句话:
dp数组(不一定是数组,也可以是有限数间的来回递推)
递推关系:dfs向下递归的公式
dp数组初始化:递归的边界
动态规划题目的基础就是:回溯——记忆化——dp(一层比一层效率高)
例:
例题
打家劫舍
#include<iostream>
using namespace std;
#include<vector>vector<int>nums = { 10,11,7,12 };vector<int>memo(100, -1);int dfs(int index) //暴力
{if (index >= nums.size()) return 0;return max( dfs(index + 2) + nums[index], dfs(index + 1) ); //这两个dfs分别代表选和不选,两种情况下的max
}int mem(int index) //记忆化
{if (memo[index] != -1) return memo[index]; //这个数下面的最大值我们已经记录了,直接返回即可if (index >= nums.size()) return 0;return memo[index]= max(mem(index + 2) + nums[index], mem(index + 1)); //记录当前下面子树最大值
}int main()
{cout << "暴力:"<< dfs(0) << endl << "记忆化:" << mem(0) << endl;vector<int>dp(nums.size(), 0); //dp.1 dp[i]就是当前房屋的maxdp[0] = nums[0]; dp[1] = max(nums[0],nums[1]);for (int i = 2; i < nums.size(); i++)dp[i] = max(dp[i - 2] + nums[i], dp[i - 1]); //画图,一定要画图,用: 10 11 7 12等试试看,会很通透int a = nums[0], b = max(nums[0], nums[1]), c = 0; //dp.2for (int i = 2; i < nums.size(); i++) {c = max(a + nums[i], b);a = b;b = c;}cout << "dp1:" << dp[nums.size() - 1] << endl;cout << "dp2:" << b << endl;return 0;
}爬楼梯(斐波那契)
递推草稿&视频:动态规划(dp)入门 | 这tm才是入门动态规划的正确方式! | dfs记忆化搜索 | 全体起立!!_哔哩哔哩_bilibili
#include<iostream>
using namespace std;
#include<vector>
#include<chrono>vector<int>memo(100, -1);
int mem(int index) //记忆化(剪枝)
{if (memo[index] != -1) return memo[index]; if (index == 1) return 1;if (index == 2) return 2;memo[index] = mem(index - 1) + mem(index - 2);return memo[index];
}int dfs(int index) //暴力
{if (index == 1) return 1;if (index == 2) return 2;return dfs(index - 1) + dfs(index - 2);
}int time(int(*k)(int),int n) //用时测试函数
{auto start = std::chrono::steady_clock::now();k(n);auto end = std::chrono::steady_clock::now();return std::chrono::duration_cast<std::chrono::milliseconds>(end - start).count();
}int main()
{int n; cin >> n;cout << dfs(n) << endl << mem(n) << endl;memo.clear(); memo.resize(100,-1);cout <<"暴力用时:"<< time(dfs, n) << " " <<"记忆化用时:" << time(mem, n) << endl;vector<int>dp(n, 0); //dp 当然也可以用三个变量来互相推dp[0] = 1, dp[1] = 2;for (int i = 2; i < n; i++)dp[i] = dp[i - 1] + dp[i - 2];cout << dp[n - 1] << endl;return 0;
}数字三角形
#include<iostream>
using namespace std;
#include<vector>//最大子路径:max 最小minvector<vector<int>>nums(100, vector<int>(100, 0));
int n;
vector<vector<int>>memo(100, vector<int>(100, -1)); int dfs(int x, int y) //暴力
{if (x >=n || y >= n ) return 0;return max(dfs(x + 1, y) + nums[x][y], dfs(x + 1, y + 1) + nums[x][y]);
}int mem(int x,int y) //记忆化(剪枝)
{if (memo[x][y]!=-1) return memo[x][y];if (x >= n || y >= n) return 0;return memo[x][y] = max(mem(x + 1, y) + nums[x][y], mem(x + 1, y + 1) + nums[x][y]);
}int main()
{cin >> n;for (int i = 0; i < n; i++)for (int j = 0; j <= i; j++)cin >> nums[i][j];cout << "暴力:" << dfs(0, 0) << endl;cout << "记忆化:" << mem(0, 0) << endl;vector<vector<int>>dp(n + 1, vector<int>(n + 1, 0)); //注意这个+1;自己思考一下for (int i = n - 1; i >= 0; i--) //dp 从下往上for (int j = 0; j < n; j++)dp[i][j]=max(dp[i+1][j+1]+nums[i][j],dp[i+1][j]+nums[i][j]);cout << "dp(从下往上递推也就是遵循从上往下递归):" << dp[0][0] << endl;return 0;
}数字三角形递推2(上往下也就是遵循下往上递归)
#include<iostream>
using namespace std;
#include<vector>int main()
{//1 从1开始int n; cin >> n;vector<vector<int>>nums(n + 1, vector<int>(n + 1, 0));//注意:建议以后动态规划题,原始数据的存储从1开始而不是0(方便),后面有从0开始for (int i = 1; i <= n; i++)for (int j = 1; j <= i; j++)cin >> nums[i][j];cout << endl;vector<vector<int>>dp(n + 1, vector<int>(n + 1, 0));for (int i = 1; i <= n; i++)for (int j = 1; j <= n; j++)dp[i][j] = max(dp[i - 1][j] + nums[i][j], dp[i - 1][j - 1] + nums[i][j]);for (auto i : dp) //强烈建议打印dp数组,观察数据是否正常{for (auto j : i)cout << j << " ";cout << endl;}//cout << dp[n][n] << endl; //err 如果直接到这里就结束就错了//这一步是干嘛?:我们从下到上dp最后答案就是dp[0][0],但是现在上到下,所以最后一整行都是和"下到上的dp[0][0]"同性质的,所以我们需要求maxint res = 0;for (int i = 1; i <= n; i++)res = max(res, dp[n][i]);cout << res << endl;//2 从0开始存储vector<vector<int>>nums2(100, vector<int>(100, 0));cin >> n;for (int i = 0; i < n; i++)for (int j = 0; j <= i; j++)cin >> nums2[i][j];cout << endl;vector<vector<int>>dp2(n + 1, vector<int>(n + 1, 0));for (int i = 1; i <= n; i++)for (int j = 1; j <= n; j++)dp2[i][j] = max(dp2[i - 1][j] + nums2[i - 1][j - 1], dp2[i - 1][j - 1] + nums2[i - 1][j - 1]);for (auto i : dp2){for (auto j : i)cout << j << " ";cout << endl;}res = 0;for (int i = 1; i <= n; i++)res = max(res, dp2[n][i]);cout << res << endl;return 0;
}
最小路径
64. 最小路径和 - 力扣(LeetCode)
和上一个数字三角形差不多
#include<iostream>
#include<vector>
using namespace std;int main()
{int x, y; cin >> x >> y;vector<vector<int>>nums(x, vector<int>(y, 0));for (int i = 0; i < x; i++)for (int j = 0; j < y; j++)cin >> nums[i][j];vector<vector<int>>dp(x + 1, vector<int>(y + 1, 0));for (int i = x - 1; i >= 0; i--)for (int j = y - 1; j >= 0; j--){if (i + 1 >= x && j + 1 >= y) dp[i][j] = nums[i][j];else if (i + 1 >= x) dp[i][j] = dp[i][j + 1] + nums[i][j];else if (j + 1 >= y) dp[i][j] = nums[i][j] + dp[i + 1][j];else dp[i][j] = max(dp[i + 1][j] + nums[i][j], dp[i][j + 1] + nums[i][j]);}cout << dp[0][0];return 0;
}相关文章:
】)
【算法——动态规划(从dfs回溯开始推导dp)】
基础理论 递归: 递:大问题分解子问题的过程 ; 归:产生答案 dp:只进行归;用已知的最底层的(递归的边界,搜索树的底),推出未知 《视频索引》 一句话&…...

不是所有洗碗机都能空气除菌 友嘉灵晶空气除菌洗碗机评测
精致的三餐让你以为生活是“享受”,可饭后那些油腻的锅碗瓢盆却成了你我美好生活的最大障碍。想要只吃美食不洗碗,那一台优秀的洗碗机就必不可少了!今天,ZOL中关村在线要评测的就是这样一台不光洗得干净更能有效除菌抑菌的洗碗机—…...
)
【Linux】如何创建yum 组(yum groups)
如何创建yum 组(yum groups) 在 yum 中创建组信息需要手动编辑并创建一个组文件,然后使用 createrepo 工具生成组信息。以下是一个详细的步骤指南: 1. 创建组信息文件 首先,创建一个 XML 文件来定义组信息。例如,创建一个名为 …...

Linux ssh远程关闭如何保持进程在后台运行的解决方案
问题描述: Unix/Linux下一般想让某个程序在后台运行,很多都是使用 nohup & 在程序结尾让程序自动运行。 使用SSH远程Linux服务器启动应用,都是使用nohup &命令,结果关闭SSH应用仍然挂断了。 我们很多程序并不象mysqld一…...

TypeScript中的泛型
在 TypeScript(简称 TS)中,泛型(Generics)是一种允许你为组件(如类、接口和函数)定义灵活、可重用的类型的方式。泛型可以看作是一种类型参数化,允许你在声明时定义一个或多个类型占…...

LeetCode-2779. 数组的最大美丽值【数组 二分查找 排序 滑动窗口】
LeetCode-2779. 数组的最大美丽值【数组 二分查找 排序 滑动窗口】 题目描述:解题思路一:滑动窗口与排序解题思路二:0解题思路三:0 题目描述: 给你一个下标从 0 开始的整数数组 nums 和一个 非负 整数 k 。 在一步操…...

RIP与OSPF发布默认路由(华为)
#交换设备 RIP与OSPF发布默认路由 合理使用默认路由可以很大程度上减少本地路由表的大小,并可以较好的隐藏一个网络中的路由信息,保护自身网络的隐秘性 另外如果在同一个路由器两端使用了不同的路由协议,那么如果不做路由引入或者发布默认…...

Android 一个改善的okHttp封装库
Android Studio 使用前,对于Android Studio的用户,可以选择添加: compile project(‘:okhttputils’) 或者 compile ‘com.zhy:okhttputils:2.0.0’ Eclipse 自行copy源码。 二、基本用法 目前基本的用法格式为: OkHttpUtils .get()…...
瓦罗兰特低价区怎么下载 瓦罗兰特低价区下载教程+免费加速器推荐
瓦罗兰特是由拳头发行的游戏,以其丰富的游戏内容和刺激的竞技体验赢得了广大玩家的喜爱。于其它热门的射击游戏不一样的是,我们在游戏中可以选择不的英雄,每一个英雄都有着自己独特的技能,我们还可以在游戏中强行改变地形帮助我们…...

lspci总结
lspci总结 大家好,我是免费搭建查券返利机器人省钱赚佣金就用微赚淘客系统3.0的小编,也是冬天不穿秋裤,天冷也要风度的程序猿!今天我们将探讨一个在 Linux 系统中常用的命令:lspci。lspci 命令用于列出当前系统中的 P…...

Android开启HTTP服务
需求:通过手机给设备升级固件,设备有WIFI 方案:升级包放到APP可以访问的目录,手机开热点并启动一个HTTP服务,设备连接手机热点,另外,设备端开启一个 telnet 服务,手机通过 telnet 登…...

NLP - word2vec详解
Word2Vec是一种用于将词汇映射到高维向量空间的自然语言处理技术。由Google在2013年提出,它利用浅层神经网络模型来学习词汇的分布式表示。Word2Vec有两种主要模型:CBOW(Continuous Bag of Words)和Skip-gram。 1. 模型介绍 Con…...

AI办公自动化:用通义千问批量翻译长篇英语TXT文档
在deepseek中输入提示词: 你是一个Python编程专家,现在要完成一个编写基于qwen-turbo模型API和dashscope库的程序脚本,具体步骤如下: 打开文件夹:F:\AI自媒体内容\待翻译; 获取里面所有TXT文档ÿ…...

一键解压,无限可能——BetterZip,您的Mac必备神器!
BetterZip for Mac 是一款高效、智能且安全的解压缩软件,专为Mac用户设计。它提供了直观易用的界面,使用户能够轻松应对各种压缩和解压缩需求。 这款软件不仅支持多种压缩格式,如ZIP、RAR、7Z等,还具备快速解压和压缩文件的能力。…...

【数学】什么是最大似然估计?如何求解最大似然估计
背景 最大似然估计(Maximum Likelihood Estimation, MLE)是一种估计统计模型参数的方法。它在众多统计学领域中被广泛使用,比如回归分析、时间序列分析、机器学习和经济学。其核心思想是:给定一个观测数据集,找到一组…...

跟张良均老师学大数据人工智能|企业项目试岗实训开营
我国高校毕业生数量连年快速增长,从2021年的909万人到2022年的1076万人,再到2023年的1158万人,预计到2024年将达到1187万人,2024年高校毕业生数量再创新高。 当年高校毕业生人数不等于进入劳动力市场的高校毕业生人数&#x…...

Pentest Muse:一款专为网络安全人员设计的AI助手
关于Pentest Muse Pentest Muse是一款专为网络安全研究人员和渗透测试人员设计和开发的人工智能AI助手,该工具可以帮助渗透测试人员进行头脑风暴、编写Payload、分析代码或执行网络侦查任务。除此之外,Pentest Muse甚至还能够执行命令行代码并以迭代方式…...
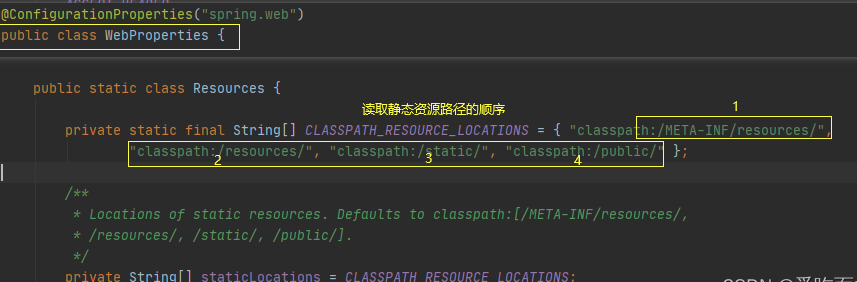
10 SpringBoot 静态资源访问
我们在开发Web项目的时候,往往会有很多静态资源,如html、图片、css等。那如何向前端返回静态资源呢? 以前做过web开发的同学应该知道,我们以前创建的web工程下面会有一个webapp的目录,我们只要把静态资源放在该目录下…...
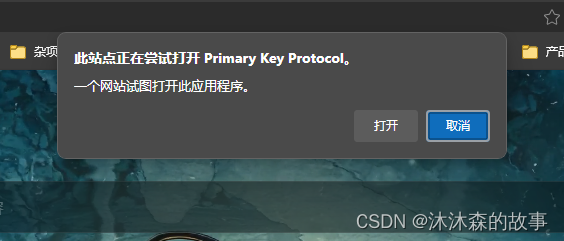
Unity 之通过自定义协议从浏览器启动本地应用程序
内容将会持续更新,有错误的地方欢迎指正,谢谢! Unity 之通过自定义协议从浏览器启动本地应用程序 TechX 坚持将创新的科技带给世界! 拥有更好的学习体验 —— 不断努力,不断进步,不断探索 TechX —— 心探索、心进…...
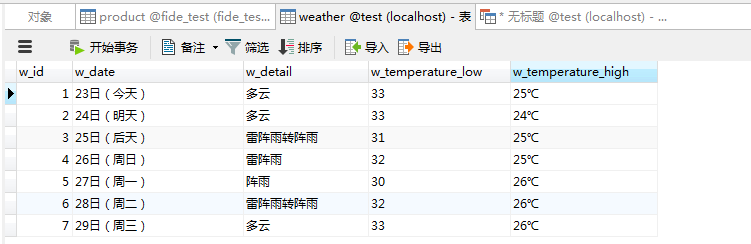
Python抓取天气信息
Python的详细学习还是需要些时间的。如果有其他语言经验的,可以暂时跟着我来写一个简单的例子。 2024年最新python教程全套,学完即可进大厂!(附全套视频 下载) (qq.com) 我们计划抓取的数据:杭州的天气信息…...

Linux应用开发之网络套接字编程(实例篇)
服务端与客户端单连接 服务端代码 #include <sys/socket.h> #include <sys/types.h> #include <netinet/in.h> #include <stdio.h> #include <stdlib.h> #include <string.h> #include <arpa/inet.h> #include <pthread.h> …...

python/java环境配置
环境变量放一起 python: 1.首先下载Python Python下载地址:Download Python | Python.org downloads ---windows -- 64 2.安装Python 下面两个,然后自定义,全选 可以把前4个选上 3.环境配置 1)搜高级系统设置 2…...

解决Ubuntu22.04 VMware失败的问题 ubuntu入门之二十八
现象1 打开VMware失败 Ubuntu升级之后打开VMware上报需要安装vmmon和vmnet,点击确认后如下提示 最终上报fail 解决方法 内核升级导致,需要在新内核下重新下载编译安装 查看版本 $ vmware -v VMware Workstation 17.5.1 build-23298084$ lsb_release…...
)
【HarmonyOS 5 开发速记】如何获取用户信息(头像/昵称/手机号)
1.获取 authorizationCode: 2.利用 authorizationCode 获取 accessToken:文档中心 3.获取手机:文档中心 4.获取昵称头像:文档中心 首先创建 request 若要获取手机号,scope必填 phone,permissions 必填 …...
中关于正整数输入的校验规则)
Element Plus 表单(el-form)中关于正整数输入的校验规则
目录 1 单个正整数输入1.1 模板1.2 校验规则 2 两个正整数输入(联动)2.1 模板2.2 校验规则2.3 CSS 1 单个正整数输入 1.1 模板 <el-formref"formRef":model"formData":rules"formRules"label-width"150px"…...

重启Eureka集群中的节点,对已经注册的服务有什么影响
先看答案,如果正确地操作,重启Eureka集群中的节点,对已经注册的服务影响非常小,甚至可以做到无感知。 但如果操作不当,可能会引发短暂的服务发现问题。 下面我们从Eureka的核心工作原理来详细分析这个问题。 Eureka的…...

智能AI电话机器人系统的识别能力现状与发展水平
一、引言 随着人工智能技术的飞速发展,AI电话机器人系统已经从简单的自动应答工具演变为具备复杂交互能力的智能助手。这类系统结合了语音识别、自然语言处理、情感计算和机器学习等多项前沿技术,在客户服务、营销推广、信息查询等领域发挥着越来越重要…...

【 java 虚拟机知识 第一篇 】
目录 1.内存模型 1.1.JVM内存模型的介绍 1.2.堆和栈的区别 1.3.栈的存储细节 1.4.堆的部分 1.5.程序计数器的作用 1.6.方法区的内容 1.7.字符串池 1.8.引用类型 1.9.内存泄漏与内存溢出 1.10.会出现内存溢出的结构 1.内存模型 1.1.JVM内存模型的介绍 内存模型主要分…...

android13 app的触摸问题定位分析流程
一、知识点 一般来说,触摸问题都是app层面出问题,我们可以在ViewRootImpl.java添加log的方式定位;如果是touchableRegion的计算问题,就会相对比较麻烦了,需要通过adb shell dumpsys input > input.log指令,且通过打印堆栈的方式,逐步定位问题,并找到修改方案。 问题…...
)
【LeetCode】3309. 连接二进制表示可形成的最大数值(递归|回溯|位运算)
LeetCode 3309. 连接二进制表示可形成的最大数值(中等) 题目描述解题思路Java代码 题目描述 题目链接:LeetCode 3309. 连接二进制表示可形成的最大数值(中等) 给你一个长度为 3 的整数数组 nums。 现以某种顺序 连接…...
