数学建模基础:非线性模型
目录
前言
一、非线性方程组
二、非线性规划
三、微分方程模型
四、非线性模型的应用
五、实例示范:传染病传播模型
实例总结
五、总结
前言
非线性模型用于描述变量之间的非线性关系,相比线性模型,其数学形式更为复杂,但可以更准确地描述实际问题。非线性模型在工程、经济、科学研究等领域有广泛应用。本文将详细介绍非线性方程组、非线性规划、微分方程模型及其应用。
一、非线性方程组
非线性方程组是多个变量的非线性方程组合,其求解通常比较复杂,需要使用数值方法。Matlab 提供了 fsolve 函数用于求解非线性方程组。
- 求解非线性方程组
- 假设我们有以下非线性方程组:
% 定义非线性方程组fun = @(x) [x(1)^2 + x(2)^2 - 1; exp(x(1)) + x(2) - 2];% 初始猜测值x0 = [0, 0];% 求解非线性方程组[x, fval] = fsolve(fun, x0);
以下表格总结了求解非线性方程组的常用方法:
| 方法 | 示例 | 说明 |
|---|---|---|
fsolve | [x, fval] = fsolve(fun, x0); | 使用 fsolve 函数求解 |
二、非线性规划
非线性规划用于求解目标函数或约束条件为非线性的问题。常见求解方法包括梯度下降法、信赖域方法等。Matlab 提供了 fminunc 和 fmincon 等函数用于求解非线性规划问题。
- 求解非线性规划(无约束)
- 假设我们需要最小化以下目标函数:
% 定义目标函数fun = @(x) x(1)^2 + x(2)^2 - cos(2*pi*x(1)) - cos(2*pi*x(2));% 初始猜测值x0 = [0, 0];% 求解无约束非线性规划问题[x, fval] = fminunc(fun, x0);
- 求解非线性规划(有约束)
- 假设我们需要最小化以上目标函数,同时约束条件为 。
% 定义目标函数fun = @(x) x(1)^2 + x(2)^2 - cos(2*pi*x(1)) - cos(2*pi*x(2));% 定义非线性约束nonlcon = @(x) deal([], x(1)^2 + x(2)^2 - 1);% 初始猜测值x0 = [0, 0];% 求解有约束非线性规划问题options = optimoptions('fmincon', 'Display', 'iter');[x, fval] = fmincon(fun, x0, [], [], [], [], [], [], nonlcon, options);
以下表格总结了求解非线性规划的常用方法:
| 方法 | 示例 | 说明 |
|---|---|---|
fminunc | [x, fval] = fminunc(fun, x0); | 求解无约束非线性规划问题 |
fmincon | [x, fval] = fmincon(fun, x0, [], [], [], [], [], [], nonlcon); | 求解有约束非线性规划问题 |
三、微分方程模型
微分方程用于描述系统的动态行为,广泛应用于物理、化学、生物等领域。常见的微分方程模型包括常微分方程(ODE)和偏微分方程(PDE)等。
- 常微分方程
- 常微分方程描述一个或多个自变量的函数及其导数之间的关系。Matlab 提供了
ode45和ode23等函数用于求解常微分方程。
- 常微分方程描述一个或多个自变量的函数及其导数之间的关系。Matlab 提供了
% 定义常微分方程dydt = @(t, y) t * y;% 求解常微分方程[t, y] = ode45(dydt, [0, 2], 1);% 绘制结果plot(t, y);title('Solution of ODE');xlabel('t');ylabel('y');grid on;
- 偏微分方程
- 偏微分方程描述多个自变量的函数及其偏导数之间的关系。Matlab 提供了
pdepe函数用于求解偏微分方程。
- 偏微分方程描述多个自变量的函数及其偏导数之间的关系。Matlab 提供了
% 定义偏微分方程m = 0;pdefun = @(x, t, u, DuDx) DuDx; % PDEicfun = @(x) sin(pi * x); % Initial conditionsbcfun = @(xl, ul, xr, ur, t) [ul; ur]; % Boundary conditions% 求解偏微分方程x = linspace(0, 1, 20);t = linspace(0, 2, 20);sol = pdepe(m, pdefun, icfun, bcfun, x, t);% 绘制结果surf(x, t, sol);title('Solution of PDE');xlabel('x');ylabel('t');zlabel('u');
以下表格总结了求解微分方程的常用方法:
| 方法 | 示例 | 说明 |
|---|---|---|
ode45 | [t, y] = ode45(dydt, [0, 2], 1); | 求解常微分方程 |
pdepe | sol = pdepe(m, pdefun, icfun, bcfun, x, t); | 求解偏微分方程 |
四、非线性模型的应用
非线性模型在实际应用中发挥了重要作用,以下是几个典型应用示例:
- 人口增长模型
- 使用 Logistic 增长模型描述人口增长。
% Logistic 增长模型r = 0.1; % 增长率K = 1000; % 环境承载力P0 = 100; % 初始人口t = 0:0.1:20; % 时间P = K ./ (1 + (K/P0 - 1) * exp(-r * t)); % Logistic 公式% 绘制结果plot(t, P);title('Logistic Growth Model');xlabel('Time');ylabel('Population');grid on;
- 传染病模型
- 使用 SIR 模型描述传染病传播。
% SIR 模型beta = 0.3; % 传染率gamma = 0.1; % 治愈率S0 = 999; % 初始易感者人口I0 = 1; % 初始感染者人口R0 = 0; % 初始治愈者人口N = S0 + I0 + R0; % 总人口% 定义 SIR 模型sir_model = @(t, y) [-beta * y(1) * y(2) / N; beta * y(1) * y(2) / N - gamma * y(2); gamma * y(2)];% 求解 SIR 模型[t, y] = ode45(sir_model, [0, 100], [S0, I0, R0]);% 绘制结果plot(t, y);title('SIR Model');xlabel('Time');ylabel('Population');legend('Susceptible', 'Infected', 'Recovered');grid on;
- 物理系统模拟
- 使用单摆模型模拟物体运动。
-
% 单摆模型g = 9.81; % 重力加速度 (m/s^2)L = 1.0; % 摆长 (m)theta0 = pi / 6; % 初始角度 (弧度)omega0 = 0; % 初始角速度 (rad/s)% 定义单摆微分方程pendulum_ode = @(t, y) [y(2); - (g / L) * sin(y(1))];% 求解单摆模型[t, y] = ode45(pendulum_ode, [0, 10], [theta0, omega0]);% 绘制结果plot(t, y(:,1));title('Pendulum Simulation');xlabel('Time (s)');ylabel('Angle (rad)');grid on;单摆模型结果如下所示:
- 金融模型
- 使用非线性模型描述期权定价问题,例如著名的 Black-Scholes 模型。
-
% Black-Scholes 模型S = 100; % 当前股票价格K = 100; % 期权执行价格r = 0.05; % 无风险利率T = 1; % 到期期限 (年)sigma = 0.2; % 波动率% 定义期权定价公式d1 = (log(S / K) + (r + sigma^2 / 2) * T) / (sigma * sqrt(T));d2 = d1 - sigma * sqrt(T);% 计算欧式看涨期权价格C = S * normcdf(d1) - K * exp(-r * T) * normcdf(d2);disp(['European Call Option Price: ', num2str(C)]);Black-Scholes 模型的结果将显示期权的价格:
European Call Option Price: 10.45 - 环境科学
- 使用非线性模型预测环境污染物的浓度变化。例如,使用 Michaelis-Menten 方程描述酶促反应速率。
-
% Michaelis-Menten 方程参数Vmax = 1.5; % 最大反应速率Km = 0.5; % 米氏常数% 底物浓度 (μM)S = 0:0.1:10;% 计算反应速率v = (Vmax * S) ./ (Km + S);% 绘制结果plot(S, v);title('Michaelis-Menten Kinetics');xlabel('Substrate Concentration (μM)');ylabel('Reaction Rate (μM/min)';grid on;下表总结了非线性模型的典型应用领域及相应的 Matlab 操作:
应用领域 说明 示例函数 人口增长模型 使用 Logistic 增长模型描述人口增长 exp,plot传染病模型 使用 SIR 模型描述传染病传播 ode45,plot物理系统模拟 使用单摆模型模拟物体运动 ode45,plot金融模型 使用 Black-Scholes 模型定价期权 normcdf,disp环境科学 使用 Michaelis-Menten 方程描述酶促反应速率 plot五、实例示范:传染病传播模型
为了更好地理解非线性模型,我们通过一个实例展示 SIR 模型在传染病传播中的应用。
假设我们需要模拟某传染病在一个1000人的社区内的传播情况,初始状态下有1个感染者,999个易感者。我们假设传染率()为0.3,治愈率()为0.1。
- 定义模型参数
-
beta = 0.3; % 传染率gamma = 0.1; % 治愈率S0 = 999; % 初始易感者人口I0 = 1; % 初始感染者人口R0 = 0; % 初始治愈者人口N = S0 + I0 + R0; % 社区总人口数 - 定义 SIR 模型
-
sir_model = @(t, y) [-beta * y(1) * y(2) / N; % 易感者变化率beta * y(1) * y(2) / N - gamma * y(2); % 感染者变化率gamma * y(2) % 治愈者变化率]; - 求解微分方程
-
% 定义求解时间范围tspan = [0, 100];% 初始条件y0 = [S0, I0, R0];% 求解 SIR 模型[t, y] = ode45(sir_model, tspan, y0); - 可视化结果
-
% 绘制结果plot(t, y);title('SIR Model of Infectious Disease Spread');xlabel('Time');ylabel('Population');legend({'Susceptible', 'Infected', 'Recovered'}, 'Location', 'Best');grid on;实例总结
通过上述实例,我们展示了非线性模型在传染病传播中的应用,并通过 Matlab 进行了建模、求解和仿真。以下是该模型应用的总结:
步骤 说明 示例 定义模型参数 定义传染率、治愈率和初始状态 beta = 0.3; gamma = 0.1; S0 = 999; I0 = 1;定义模型 定义 SIR 模型 sir_model = @(t, y) [...];求解微分方程 使用 ode45求解微分方程[t, y] = ode45(sir_model, tspan, y0);可视化结果 绘制易感者、感染者和治愈者人口随时间变化的曲线 plot(t, y); title(...); xlabel(...);五、总结
本文详细介绍了非线性模型及其在实际中的应用,包括非线性方程组、非线性规划、微分方程模型及其应用领域。通过实际案例,我们演示了如何使用 Matlab 建立和求解非线性模型,如人口增长模型、传染病模型、物理系统模拟和金融模型等。
使用非线性模型可以更准确地描述和预测复杂系统的行为,掌握这些工具和方法将大大提高我们在科学研究和工程实践中的建模能力和决策水平。
下表总结了非线性模型的基础知识和应用领域:
模型类型 说明 示例函数 非线性方程组 用于求解多个变量的非线性方程 fsolve(fun, x0);非线性规划(无约束) 用于求解无约束非线性优化问题 fminunc(fun, x0);非线性规划(有约束) 用于求解有约束非线性优化问题 fmincon(fun, x0, [], [], [], [], [], [], nonlcon);常微分方程 用于描述系统的动态行为,通过ODE求解 ode45(dydt, tspan, y0);偏微分方程 用于描述多个变量的动态行为,通过PDE求解 pdepe(m, pdefun, icfun, bcfun, x, t);人口增长模型 Logistic增长模型描述人口增长 plot(t, P);传染病模型 SIR 模型描述传染病传播 ode45(sir_model, tspan, y0);物理系统模拟 单摆模型描述物体运动 ode45(pendulum_ode, tspan, y0);金融模型 Black-Scholes 模型定价期权 normcdf(d1); normcdf(d2);环境科学 Michaelis-Menten 方程描述酶促反应速率 plot(S, v);
相关文章:

数学建模基础:非线性模型
目录 前言 一、非线性方程组 二、非线性规划 三、微分方程模型 四、非线性模型的应用 五、实例示范:传染病传播模型 实例总结 五、总结 前言 非线性模型用于描述变量之间的非线性关系,相比线性模型,其数学形式更为复杂,但…...
Kotlin 语言基础学习
什么是Kotlin ? Kotiln翻译为中文是:靠他灵。它是由JetBrains 这家公司开发的,JetBrains 是一家编译器软件起家的,例如常用的WebStorm、IntelliJ IDEA等软件。 Kotlin官网 JetBrains 官网 Kotlin 语言目前的现状: 目前Android 已将Kotlin 作为官方开发语言。 Spring 框…...

Kafka 之 KRaft —— 配置、存储工具、部署注意事项、缺失的特性
目录 一. 前言 二. 配置(Configuration) 2.1. 处理者角色(Process Roles) 2.2. 控制器(controller) 2.3. 存储工具(Storage Tool) 2.4. 调试(Debugging)…...

专业和学校到底怎么选,兴趣和知名度到底哪个重要?
前言 2024高考已经落下帷幕,再过不久就到了激动人心的查分和填报志愿的时刻,在那天到来,小伙伴们就要根据自己的分数选取院校和专业,接下来我就以参加22年(破防年)河南高考的大二生来讲述一下我自己对于如何选取院校和专业的看法以…...

【MySQL】数据库
数据库概述 【MySQL】数据库概述-CSDN博客 数据库基本操作 【MySQL】数据库基本操作-CSDN博客 数据表基本操作 【MySQL】数据表基本操作-CSDN博客 约束 【MySQL】约束-CSDN博客 基本增删改查 【MySQL】基本增删改查-CSDN博客 多表操作 【MySQL】多表操作-CSDN博客 视图 …...

D111FCE01LC2NB70带流量调节派克比例阀
D111FCE01LC2NB70带流量调节派克比例阀 派克比例阀:由于采用(秉圣135陈工6653询3053)电液混合控制技术,响应速度更快、精度更高、控制更平稳。同时,由于采用高质量的材料制造,具有较高的承压能力和抗磨损性…...
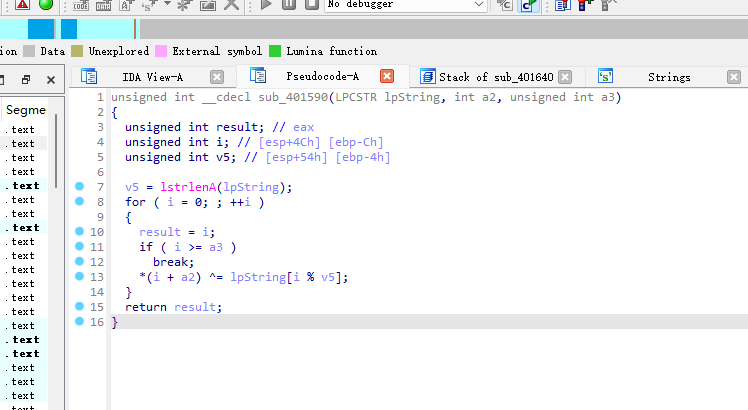
buuctf-findKey
exe文件 运行发现这个窗口,没有任何消息 32位 进入字符串就发现了flag{ 左边红色代表没有F5成功 我们再编译一下(选中红色的全部按p) LRESULT __stdcall sub_401640(HWND hWndParent, UINT Msg, WPARAM wParam, LPARAM lParam) {int v5; // eaxsize_t v6; // eaxDWORD v7; /…...

针对oracle系列数据库慢数据量大的问题
-- 确保索引存在 create index idx_risk_assessment_hazard on risk_assessment_hazard(data_time, perception_id); create index idx_risk_dispose_base_info on risk_dispose_base_info(perception_id); -- 使用并行查询和with子句进行优化 explain plan for with t2 as (se…...
Nginx-Rewrite
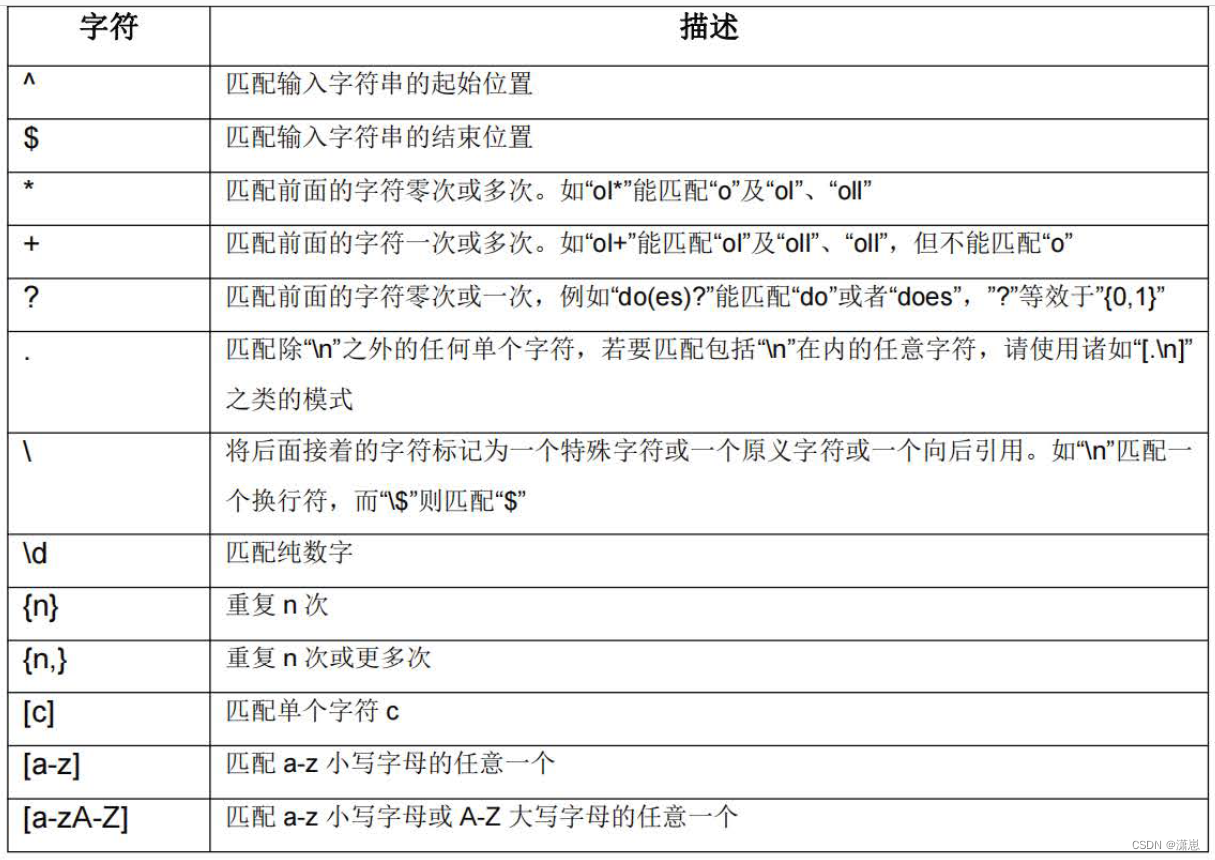
1、Rewrite的定义 rewrite功能就是使用nginx提供的全局变量或自己设置的变量,结合正则表达式和标志位实现url重写以及重定向。rewrite只能放在 server { }, location { }, if { }中,并且只能对域名后边的除去传递的参数外的字符串起作用。 例如location…...

2024 年 Python 基于 Kimi 智能助手 Moonshot Ai 模型搭建微信机器人(更新中)
注册 Kimi 开放平台 Kimi:https://www.moonshot.cn/ Kimi智能助手是北京月之暗面科技有限公司(Moonshot AI)于2023年10月9日推出的一款人工智能助手,主要为用户提供高效、便捷的信息服务。它具备多项强大功能,包括多…...
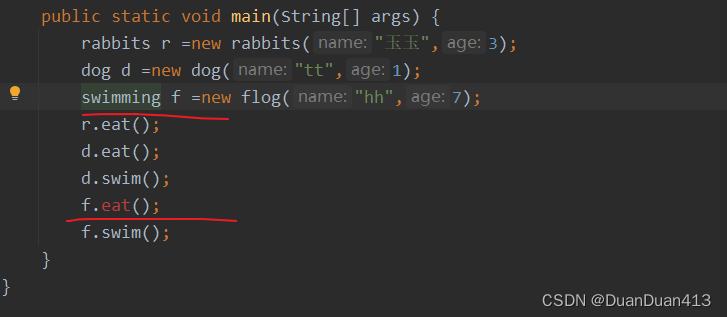
关于接口多态,何时使用接口名创建对象?何时使用子类创建对象?
接口创建对象只能创建他的实现类,所以会出现两种创建方式: 1、接口 对象名 new 类名 2、子类对象 对象名 new 类名 举个例子,swimming是一个接口,flog是他的一个实现类,重写了swimming的eat()方法 子类对象 对象名…...

短视频热恋进行时:成都柏煜文化传媒有限公司
短视频热恋进行时:情感与创意的碰撞与融合 在数字时代的浪潮中,短视频以其独特的魅力,成为了当代人表达情感、分享生活的新宠。它如同一个浓缩的时空胶囊,将那些瞬间的美好、感人的故事、创意的火花,封装在短短几十秒…...
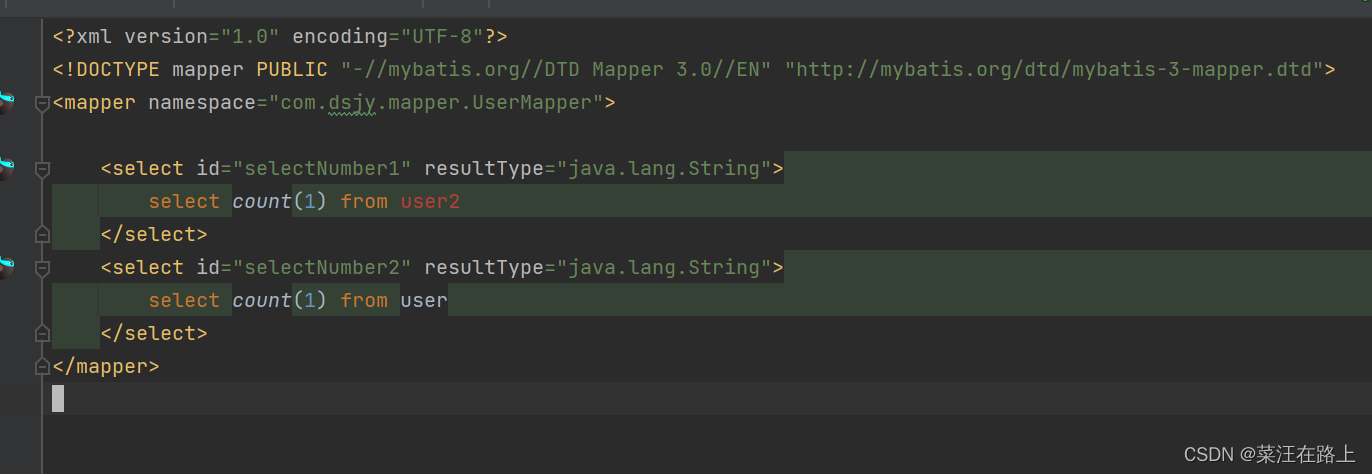
springBoot多数据源使用、配置
又参加了一个新的项目,虽然是去年做的项目,拿来复用改造,但是也学到了很多。这个项目会用到其他项目的数据,如果调用他们的接口取数据,我还是觉得太麻烦了。打算直接配置多数据源。 然后去另一个数据库系统中取出数据…...
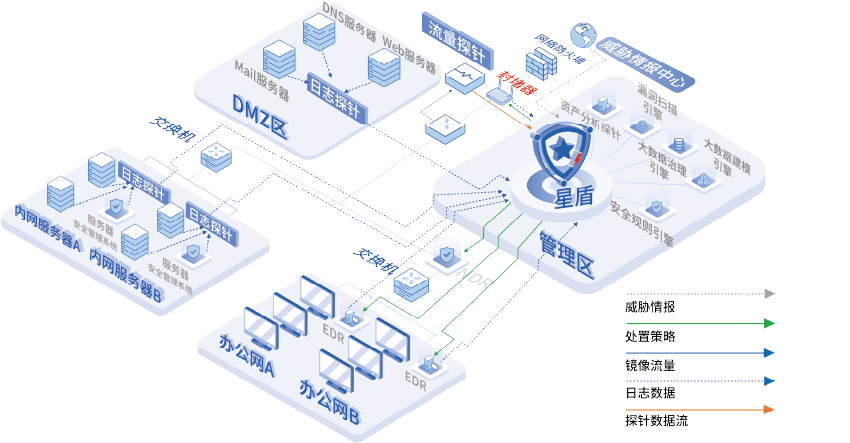
打破安全设备孤岛,多源威胁检测与响应(XDR)如何构建一体化安全防线
在数字化和信息化迅猛发展的当下,安全设备孤岛现象成为网络安全治理中的一大挑战。在多元化的市场环境中,不同厂商的安全设备因数据格式与系统兼容性的差异,导致信息流通受阻、共享困难,形成孤立的安全防线。 安全设备孤岛现象不仅…...
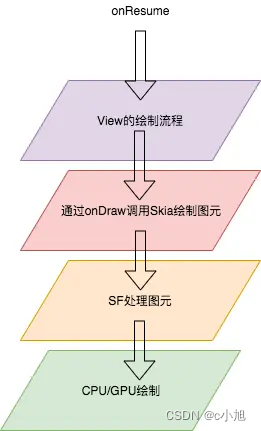
Android SurfaceFlinger——概述(一)
一、基础介绍 SurfaceFlinger 是 Android 系统中的一个关键组件,负责管理屏幕显示的合成和渲染。 服务角色:SurfaceFlinger 作为一个系统服务独立运行,它不依赖于任何应用程序进程,而是由系统启动并持续运行。窗口管理:…...
工业 web4.0,UI 风格令人赞叹
工业 web4.0,UI 风格令人赞叹...

HarmonyOS 角落里的知识 —— 状态管理
一、前言 在探索 HarmonyOS 的过程中,我们发现了许多有趣且实用的功能和特性。有些总是在不经意间或者触类旁通的找到。或者是某些开发痛点。其中,状态管理是ArkUI开发非常核心的一个东西,我们进行了大量的使用和测试遇到了许多奇奇怪怪的问…...

TDengine数据迁移
前言 taosdump 是一个支持从运行中的 TDengine 集群备份数据并将备份的数据恢复到相同或另一个运行中的 TDengine 集群中的工具应用程序。 taosdump 可以用数据库、超级表或普通表作为逻辑数据单元进行备份,也可以对数据库、超级 表和普通表中指定时间段内的数据记录…...

使用ZIP包安装MySQL及配置教程
在本教程中,我们将指导您完成使用ZIP包安装MySQL的过程,并对配置文件进行必要的修改,以及解决可能遇到的问题。本示例以MySQL 5.7.44为例,但步骤同样适用于其他版本如MySQL 8.3.0等。请根据实际需要选择适合的版本下载:…...

Java基础入门day64
day64 web项目 数据库设计 在小米商城主页,主要的内容是多种商品类型的展示,分别有手机,智能穿戴,笔记本平板,家电,生活电器,厨房电器,智能家具等大的七个分类,根据这个…...
详解)
后进先出(LIFO)详解
LIFO 是 Last In, First Out 的缩写,中文译为后进先出。这是一种数据结构的工作原则,类似于一摞盘子或一叠书本: 最后放进去的元素最先出来 -想象往筒状容器里放盘子: (1)你放进的最后一个盘子(…...

conda相比python好处
Conda 作为 Python 的环境和包管理工具,相比原生 Python 生态(如 pip 虚拟环境)有许多独特优势,尤其在多项目管理、依赖处理和跨平台兼容性等方面表现更优。以下是 Conda 的核心好处: 一、一站式环境管理:…...

深入剖析AI大模型:大模型时代的 Prompt 工程全解析
今天聊的内容,我认为是AI开发里面非常重要的内容。它在AI开发里无处不在,当你对 AI 助手说 "用李白的风格写一首关于人工智能的诗",或者让翻译模型 "将这段合同翻译成商务日语" 时,输入的这句话就是 Prompt。…...

在鸿蒙HarmonyOS 5中实现抖音风格的点赞功能
下面我将详细介绍如何使用HarmonyOS SDK在HarmonyOS 5中实现类似抖音的点赞功能,包括动画效果、数据同步和交互优化。 1. 基础点赞功能实现 1.1 创建数据模型 // VideoModel.ets export class VideoModel {id: string "";title: string ""…...

8k长序列建模,蛋白质语言模型Prot42仅利用目标蛋白序列即可生成高亲和力结合剂
蛋白质结合剂(如抗体、抑制肽)在疾病诊断、成像分析及靶向药物递送等关键场景中发挥着不可替代的作用。传统上,高特异性蛋白质结合剂的开发高度依赖噬菌体展示、定向进化等实验技术,但这类方法普遍面临资源消耗巨大、研发周期冗长…...

Go 语言接口详解
Go 语言接口详解 核心概念 接口定义 在 Go 语言中,接口是一种抽象类型,它定义了一组方法的集合: // 定义接口 type Shape interface {Area() float64Perimeter() float64 } 接口实现 Go 接口的实现是隐式的: // 矩形结构体…...

oracle与MySQL数据库之间数据同步的技术要点
Oracle与MySQL数据库之间的数据同步是一个涉及多个技术要点的复杂任务。由于Oracle和MySQL的架构差异,它们的数据同步要求既要保持数据的准确性和一致性,又要处理好性能问题。以下是一些主要的技术要点: 数据结构差异 数据类型差异ÿ…...

如何将联系人从 iPhone 转移到 Android
从 iPhone 换到 Android 手机时,你可能需要保留重要的数据,例如通讯录。好在,将通讯录从 iPhone 转移到 Android 手机非常简单,你可以从本文中学习 6 种可靠的方法,确保随时保持连接,不错过任何信息。 第 1…...

c#开发AI模型对话
AI模型 前面已经介绍了一般AI模型本地部署,直接调用现成的模型数据。这里主要讲述讲接口集成到我们自己的程序中使用方式。 微软提供了ML.NET来开发和使用AI模型,但是目前国内可能使用不多,至少实践例子很少看见。开发训练模型就不介绍了&am…...

如何在网页里填写 PDF 表格?
有时候,你可能希望用户能在你的网站上填写 PDF 表单。然而,这件事并不简单,因为 PDF 并不是一种原生的网页格式。虽然浏览器可以显示 PDF 文件,但原生并不支持编辑或填写它们。更糟的是,如果你想收集表单数据ÿ…...
