当前位置： 首页 > news >正文

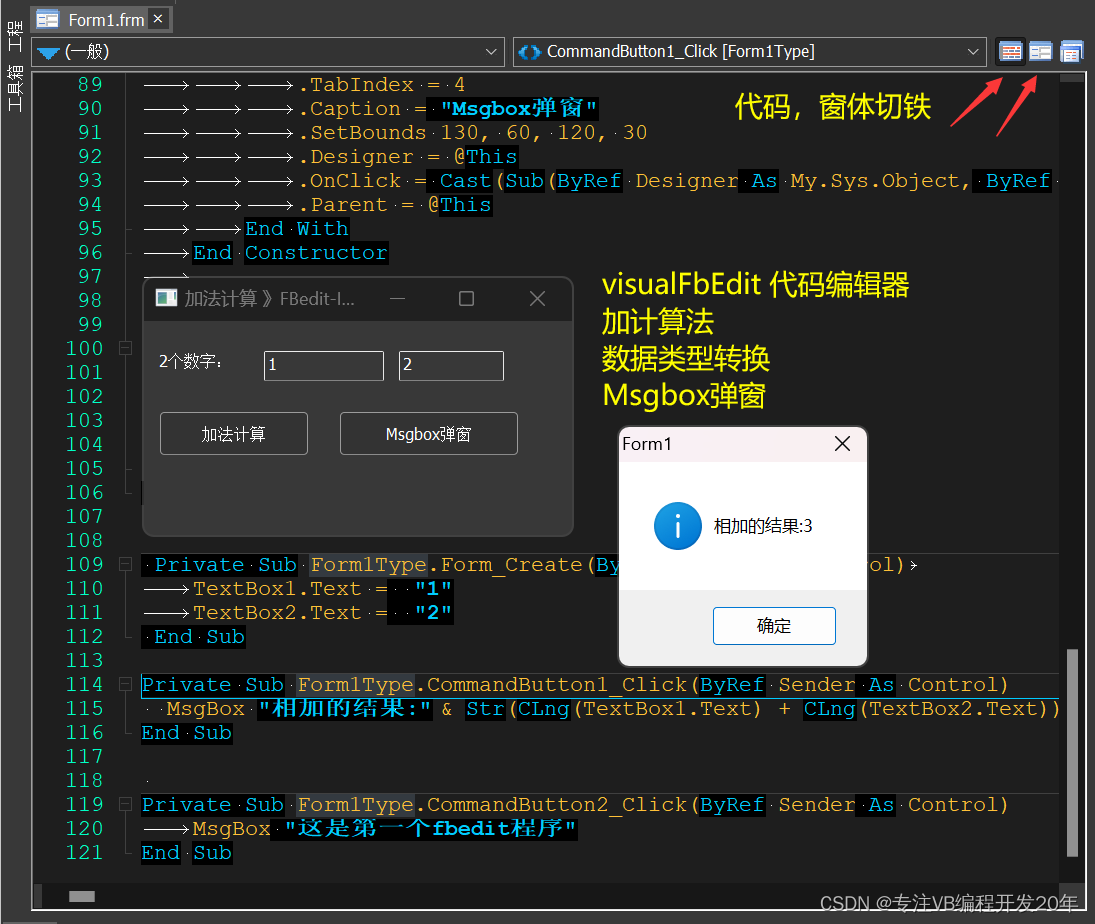
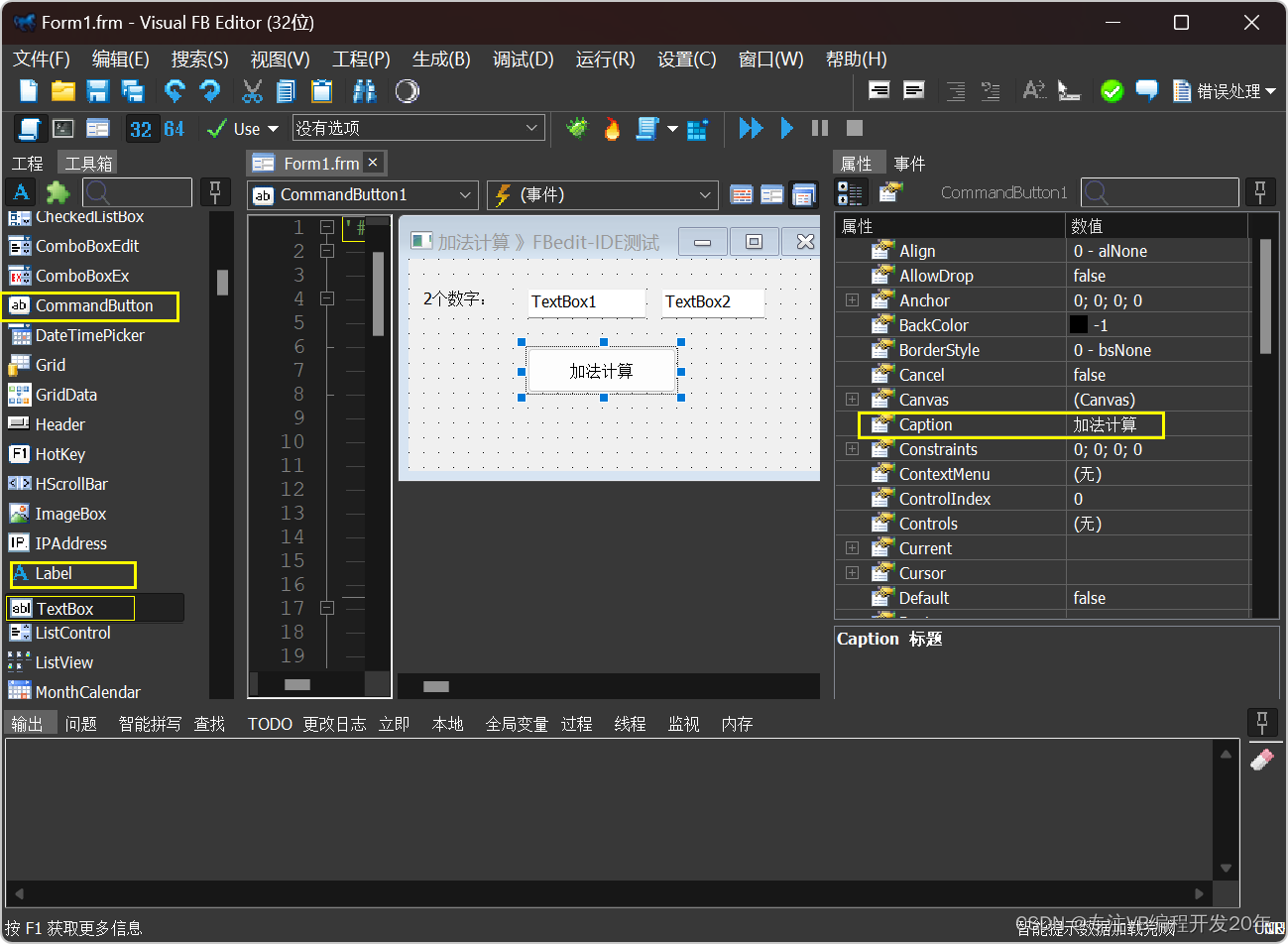
开源VisualFbeditor中文版,vb7 IDE,VB6升级64位跨平台开发安卓APP,Linux程序

news 2025/10/15 4:51:36

吴涛老矣，社区苦无64位易语言，用注入DLL增强菜单，做成VS一样的界面
终归是治标不治本，一来会报毒，二来闭源20年没更新了
开源的VB7，欢迎易语言的铁粉进群：1032313876
【Freebasic编程语言】编绎器开源，支持跨平台Linux/安卓开发
-----------安装注意，不要安装到中文目录，不要带空格的路径
比如 D:\VisualFBEditor  然后发送桌面快捷方式：VisualFBEditorPro32.exe

Download: GitCode - VisualFBEditor登录后下载当前目录

>>官方社区-意见BUG反馈 VisualFBEditor - IDE for  freebasic.net

Github开源项目 https://github.com/XusinboyBekchanov/VisualFBEditor

080a3dddc6fb42899cf01bc5ed6a04b5.png

f0f2a2b2e1ee42e4a0b4fc29f817c20e.png
==========================
第2个项目twinbasic不开源，火速开发中，功能最像VB6
32位免费使用，64位会有5秒的弹窗
VB7/64位VB6开发工具office插件开发-twinbasic【含汉化工具】
https://blog.csdn.net/xiaoyao961/article/details/139558711
全新的VB7，twinbasic，支持64位开发，支持EXCEL插件开发，老外连续3年闭关修练终成正果

官方下载：https://github.com/twinbasic/twinbasic/releases

GITHUB TB最新问题反馈
https://github.com/twinbasic/twinbasic/issues
大家要每天用2小时，把问题反馈给首席设计师，把BUG都消灭掉。
以后要是没人开发了，BUG也没人解决，自已最痛苦

Twinbasic论坛新版发布和反馈
https://www.vbforums.com/showthread.php?905047

相关文章：

开源VisualFbeditor中文版,vb7 IDE,VB6升级64位跨平台开发安卓APP,Linux程序

吴涛老矣，社区苦无64位易语言，用注入DLL增强菜单，做成VS一样的界面 终归是治标不治本，一来会报毒，二来闭源20年没更新了 开源的VB7，欢迎易语言的铁粉进群：1032313876 【Freebasic编程语言】编绎…...

编程日记 2024/6/20 2:30:29

github安全问题token和sshkeys

文章目录 sshkeys问题问题方法一：方法二：获取密钥添加密钥token问题问题:生成tokens设置tokenssshkeys问题 问题 当我们git clone代码时，会报如下错误，此时有2种解决方法。 git clone git@github.com:gjianw217/xboard-uboot.git Cloning into xboard-uboot... Permissio…...

编程日记 2024/6/20 2:29:27

超详细的selenium使用指南

🍅 视频学习：文末有免费的配套视频可观看 🍅 点击文末小卡片 ，免费获取软件测试全套资料，资料在手，涨薪更快 概述 selenium是网页应用中最流行的自动化测试工具，可以用来做自动化测试或者浏览器…...

编程日记 2024/6/20 2:28:26

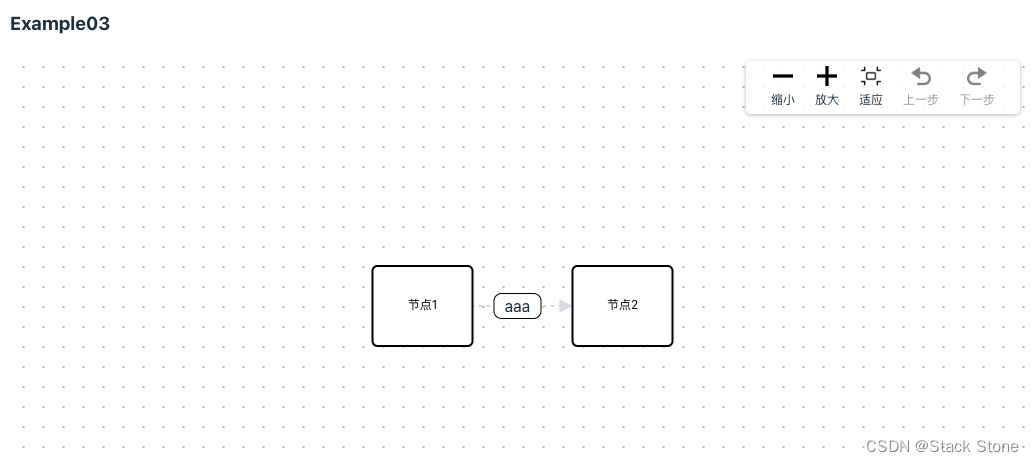
LogicFlow 学习笔记——1. 初步使用 LogicFlow

什么是 LogicFlow LogicFlow 是一个开源的前端流程图编辑器和工作流引擎，旨在帮助开发者和业务人员在网页端创建、编辑和管理复杂的业务流程和工作流。它提供了一个直观的界面和强大的功能，使得设计和管理工作流变得更加高效和便捷。 官网地址&#xff…...

编程日记 2024/6/20 2:26:23

场外个股期权通道业务是什么意思？

今天带你了解场外个股期权通道业务是什么意思？场外个股期权业务是指在沪深交易所之外进行的个股期权交易。它是一种非标准化的合约，不在交易所内进行交割。 场外个股期权通道业务，是指投资者通过与场外个股期权机构通道签订合约，购…...

编程日记 2024/6/20 2:25:22

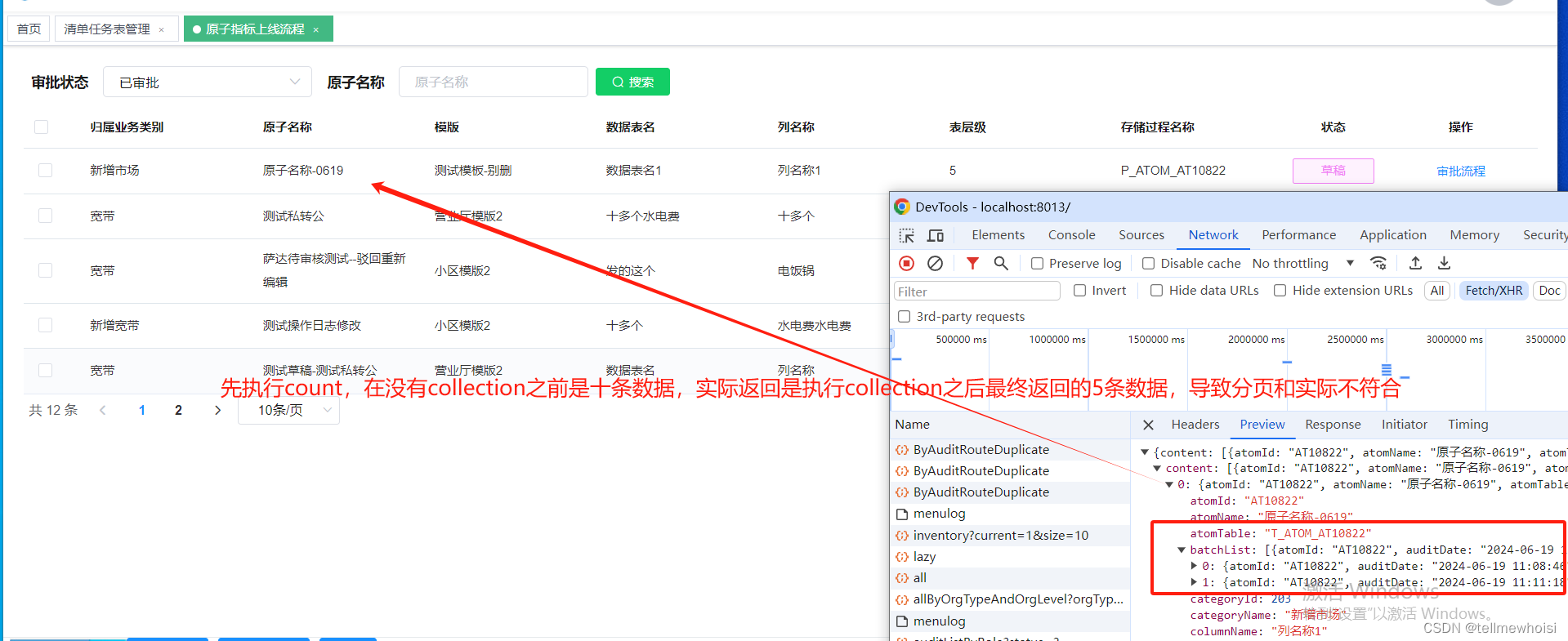
分页插件结合collection标签后分页数量不准确的问题

问题1:不使用collection 聚合分页正确 简单列子 T_ATOM_DICT表有 idname1原子12原子23原子34原子45原子56原子6 T_ATOM_DICT_AUDIT_ROUTE表审核记录表有 idaudit1拒绝1通过4拒绝 我要显示那些原子审核了,我把两个表inner join 就是那些原子审核过了 idnameaudit1原子1拒绝…...

编程日记 2024/6/20 2:24:21

git diff 命令

目录标题 [Q&A] git diff 作用常见用法比较工作目录与暂存区比较暂存区与最近一次提交比较工作目录与最近一次提交比较两个具体的提交之间差异 [Q&A] git diff 作用 git diff 用于展示不同版本之间文件内容的变化。 常见用法 比较工作目录与暂存区 显示工作目录中尚…...

编程日记 2024/6/20 2:22:18

Code Review常用术语

CR: Code Review. 请求代码审查。PR： pull request. 拉取请求，给其他项目提交代码。MR： merge request. 合并请求。LGTM： Looks Good To Me.对我来说，还不错。表示认可这次PR，同意merge合并代码到远程仓库。…...

编程日记 2024/6/20 2:21:16

HashMap 源码中的巧妙小技巧

根据容量计算大于容量的最小的哈希表的大小(table的length)，这里的length需要满足length2^n，也就是我们需要根据容量算出最小的n的值 static final int tableSizeFor(int cap) {int n cap - 1;n | n >>> 1;n | n >>> 2;n | n >&g…...

编程日记 2024/6/20 2:20:14

极具吸引力的小程序 UI 风格

极具吸引力的小程序 UI 风格...

编程日记 2024/6/20 2:18:12

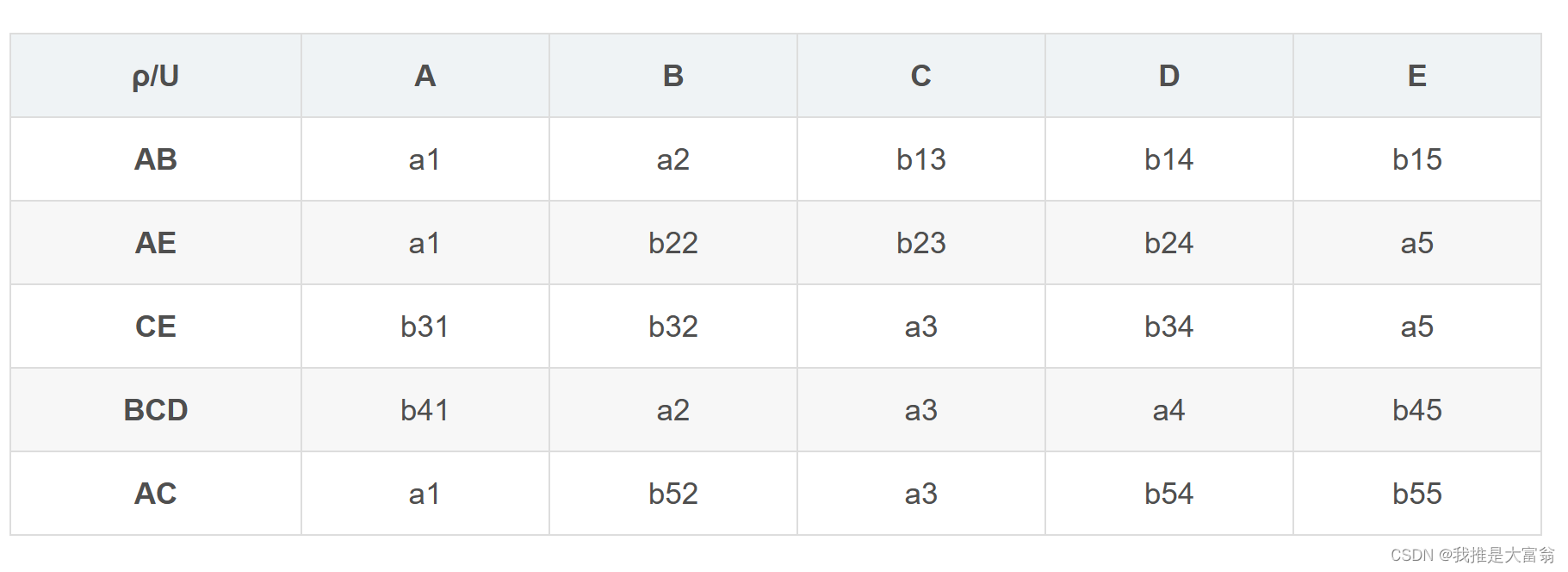
数据库 | 试卷五试卷六试卷七

1. 主码不相同！相同的话就不能唯一标识非主属性了 2.从关系规范化理论的角度讲，一个只满足 1NF 的关系可能存在的四方面问题 是： 数据冗余度大，插入异常，修改异常，删除异常 3.数据模型的三大要素是什么&…...

编程日记 2024/6/20 2:16:09

网页五子棋对战项目测试(selenium+Junit5)

目录 网页五子棋对战项目介绍 网页五子棋对战测试的思维导图​ 网页五子棋对战的UI自动化测试 测试一：测试注册界面 测试二：测试登陆界面 测试三：测试游戏大厅界面 测试四：测试游戏房间界面以及观战房间界面 测试五&#…...

编程日记 2024/6/20 2:15:08

stable diffusion 局部重绘 reference-only api 接口调试

webUI api payload 插件生成的接口参数不准确，reference-only 的image不是对象，就是不同字符串字段，直接传，不是套image。 综上，那个插件参数不确定，应直接看插件的源码，看它接受什么参数 错误…...

编程日记 2024/6/20 2:14:07

浪潮信息内存故障预警技术再升级 服务器稳定性再获提升

浪潮信息近日对其内存故障智能预警修复技术进行了全面升级，再次取得技术突破。此次升级后，公司服务器的宕机率实现了80%锐降，再次彰显了浪潮信息在服务器技术领域的卓越能力。 浪潮信息全新升级服务器内存故障智能预警修复技术MUPR (Memory …...

编程日记 2024/6/20 2:12:04

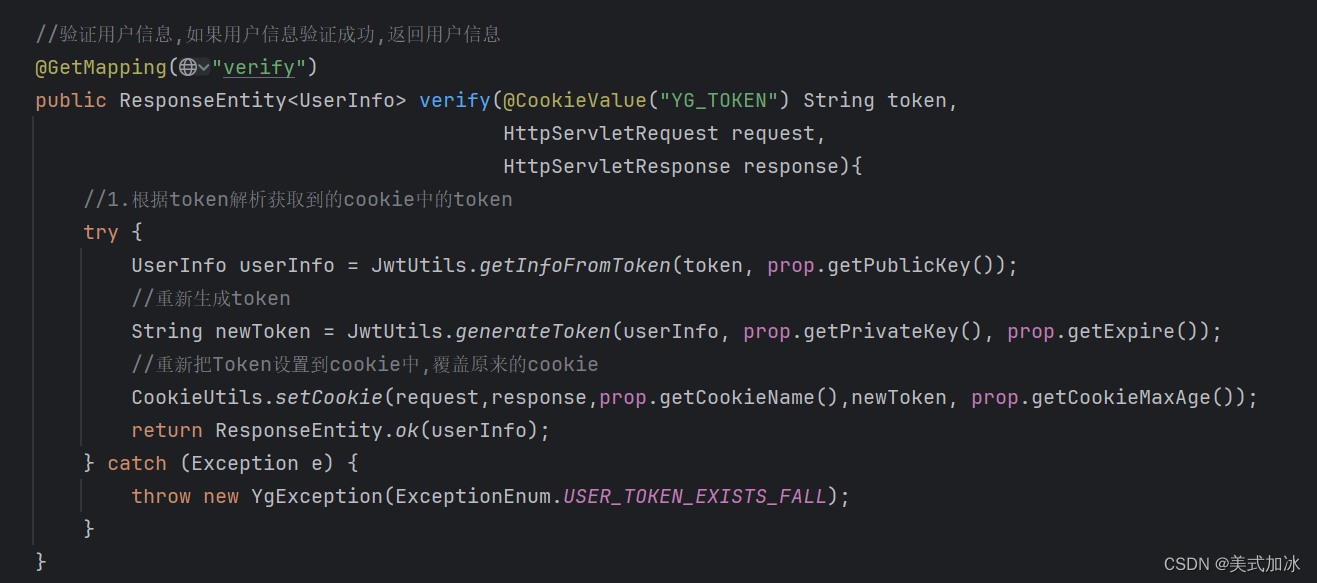
JWT整合Gateway实现鉴权(RSA与公私密钥工具类)

一.业务流程 1.使用RSA生成公钥和私钥。私钥保存在授权中心，公钥保存在网关(gateway)和各个信任微服务中。 2.用户请求登录。 3.授权中心进行校验，通过后使用私钥对JWT进行签名加密。并将JWT返回给用户 4.用户携带JWT访问 5.gateway直接通过公钥解密JWT进…...

编程日记 2024/6/20 2:11:03

vue实现全屏screenfull-封装组件

1. 安装依赖 npm install --save screenfull 2. 引用 import screenfull from "screenfull" 3.封装fullScreen/index: <template><div><el-tooltip v-if"!content" effect"dark" :content"fullscreenTips" placement&…...

编程日记 2024/6/20 2:10:01

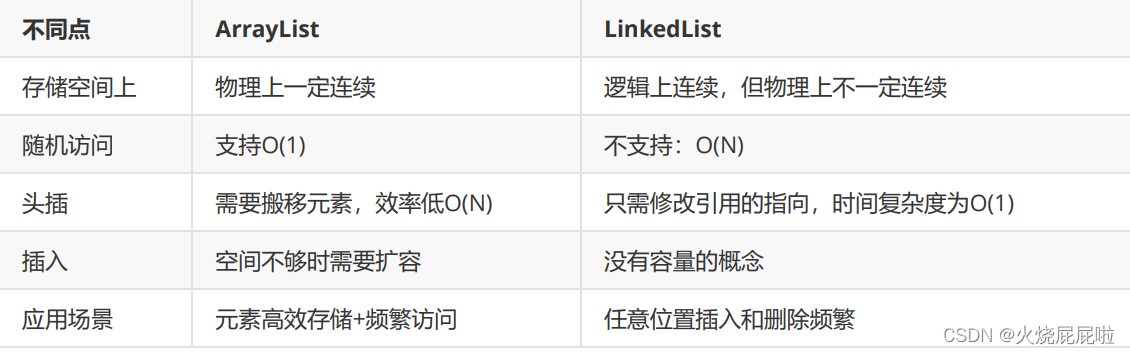
【LinkedList与链表】

目录 1&#xff0c;ArrayList的缺陷 2&#xff0c;链表 2.1 链表的概念及结构 2.2 链表的实现 2.2.1 无头单向非循环链表实现 3&#xff0c;LinkedList的模拟实现 3.1 无头双向链表实现 4&#xff0c;LinkedList的使用 4.1 什么是LinkedList 4.2 LinkedList的使用 5…...

编程日记 2024/6/20 2:07:58

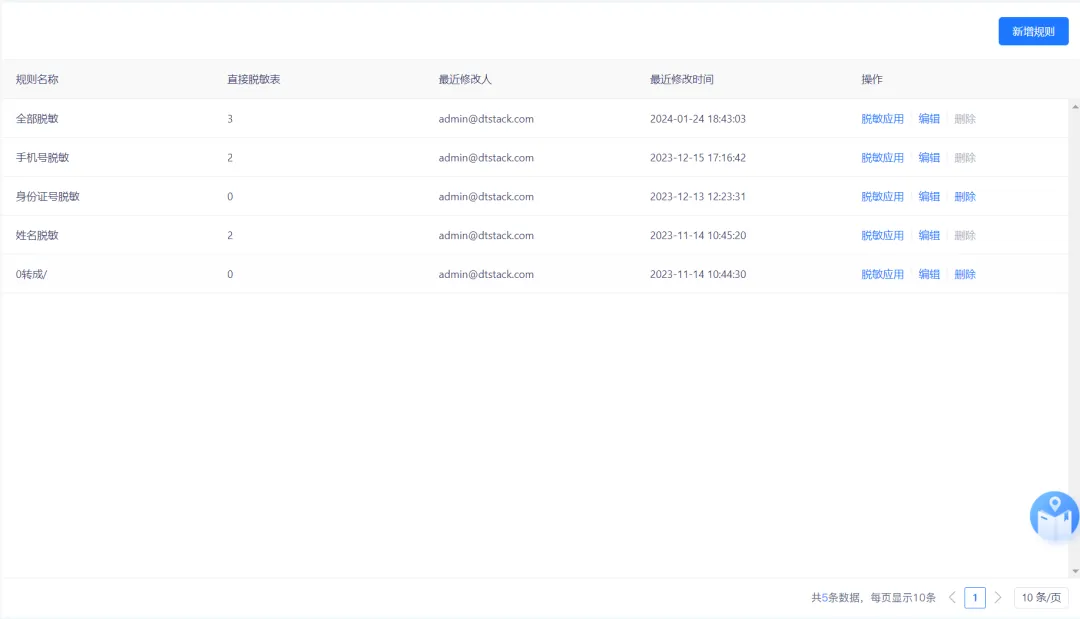
为数据安全护航，袋鼠云在数据分类分级上的探索实践

在大数据时代&#xff0c;数据具有多源异构的特性&#xff0c;且价值各异&#xff0c;企业需依据数据的重要性、价值指数等予以区分&#xff0c;以利采取不同的数据保护举措&#xff0c;避免数据泄露。故而&#xff0c;数据分类分级管理属于数据安全保护中极为重要的环节之一。…...

编程日记 2024/6/20 2:06:56

Spring 循环依赖详解

Spring 循环依赖详解 1. 引言 在Spring框架中&#xff0c;依赖注入&#xff08;Dependency Injection, DI&#xff09;是其核心功能之一&#xff0c;它通过配置来管理对象的创建和它们之间的依赖关系。然而&#xff0c;在复杂的应用程序中&#xff0c;开发人员有时会遇到循环…...

编程日记 2024/6/20 2:05:54

项目经理真的不能太“拧巴”

前期的项目经理经常是“拧巴”的&#xff0c;就是心里纠结、思路混乱、行动迟缓。对于每天需要面对各种挑战、协调各方资源、确保项目顺利进行的项目经理来说&#xff0c;这种“拧巴”不仅会让自己陷入内耗中&#xff0c;还会让项目出大问题。 项目计划总是改来改去&#xff0…...

编程日记 2024/6/20 2:04:52

Leetcode 3576. Transform Array to All Equal Elements

Leetcode 3576. Transform Array to All Equal Elements 1. 解题思路2. 代码实现 题目链接&#xff1a;3576. Transform Array to All Equal Elements 1. 解题思路 这一题思路上就是分别考察一下是否能将其转化为全1或者全-1数组即可。 至于每一种情况是否可以达到&#xf…...

编程新知 2025/9/17 7:25:07

基于Java Swing的电子通讯录设计与实现：附系统托盘功能代码详解

JAVASQL电子通讯录带系统托盘 一、系统概述 本电子通讯录系统采用Java Swing开发桌面应用&#xff0c;结合SQLite数据库实现联系人管理功能&#xff0c;并集成系统托盘功能提升用户体验。系统支持联系人的增删改查、分组管理、搜索过滤等功能&#xff0c;同时可以最小化到系统…...

编程新知 2025/10/4 20:58:43

安宝特案例丨Vuzix AR智能眼镜集成专业软件，助力卢森堡医院药房转型，赢得辉瑞创新奖

在Vuzix M400 AR智能眼镜的助力下&#xff0c;卢森堡罗伯特舒曼医院&#xff08;the Robert Schuman Hospitals, HRS&#xff09;凭借在无菌制剂生产流程中引入增强现实技术&#xff08;AR&#xff09;创新项目&#xff0c;荣获了2024年6月7日由卢森堡医院药剂师协会&#xff0…...

编程新知 2025/9/28 3:35:11

如何更改默认 Crontab 编辑器 ？

在 Linux 领域中&#xff0c;crontab 是您可能经常遇到的一个术语。这个实用程序在类 unix 操作系统上可用&#xff0c;用于调度在预定义时间和间隔自动执行的任务。这对管理员和高级用户非常有益&#xff0c;允许他们自动执行各种系统任务。 编辑 Crontab 文件通常使用文本编…...

编程新知 2025/10/1 7:32:54

Web中间件--tomcat学习

Web中间件–tomcat Java虚拟机详解 什么是JAVA虚拟机 Java虚拟机是一个抽象的计算机&#xff0c;它可以执行Java字节码。Java虚拟机是Java平台的一部分&#xff0c;Java平台由Java语言、Java API和Java虚拟机组成。Java虚拟机的主要作用是将Java字节码转换为机器代码&#x…...

编程新知 2025/9/13 18:20:34

uniapp 字符包含的相关方法

在uniapp中&#xff0c;如果你想检查一个字符串是否包含另一个子字符串&#xff0c;你可以使用JavaScript中的includes()方法或者indexOf()方法。这两种方法都可以达到目的&#xff0c;但它们在处理方式和返回值上有所不同。 使用includes()方法 includes()方法用于判断一个字…...

编程新知 2025/9/28 19:00:18

第7篇：中间件全链路监控与 SQL 性能分析实践

7.1 章节导读 在构建数据库中间件的过程中&#xff0c;可观测性 和 性能分析 是保障系统稳定性与可维护性的核心能力。 特别是在复杂分布式场景中&#xff0c;必须做到&#xff1a; &#x1f50d; 追踪每一条 SQL 的生命周期&#xff08;从入口到数据库执行&#xff09;&#…...

编程新知 2025/8/8 6:07:28

stm32wle5 lpuart DMA数据不接收

配置波特率9600时&#xff0c;需要使用外部低速晶振...

编程新知 2025/10/13 9:20:12

消防一体化安全管控平台：构建消防“一张图”和APP统一管理

在城市的某个角落&#xff0c;一场突如其来的火灾打破了平静。熊熊烈火迅速蔓延&#xff0c;滚滚浓烟弥漫开来&#xff0c;周围群众的生命财产安全受到严重威胁。就在这千钧一发之际&#xff0c;消防救援队伍迅速行动&#xff0c;而豪越科技消防一体化安全管控平台构建的消防“…...

编程新知 2025/10/15 1:22:11

高考志愿填报管理系统---开发介绍

高考志愿填报管理系统是一款专为教育机构、学校和教师设计的学生信息管理和志愿填报辅助平台。系统基于Django框架开发&#xff0c;采用现代化的Web技术&#xff0c;为教育工作者提供高效、安全、便捷的学生管理解决方案。 ## &#x1f4cb; 系统概述 ### &#x1f3af; 系统定…...

编程新知 2025/10/5 0:21:28