当前位置： 首页 > news >正文

linux配置Vnc Server给Windows连接

news 2026/2/11 1:56:42

1. linux 安装必要vnc server和桌面组件

 sudo apt -y install tightvncserversudo apt install xfce4 xfce4-goodies

2. linux 配置vncserver密码

#bash
vncserver
  • 参考: https://cn.linux-console.net/?p=21846#google_vignette

3. 将启动桌面命令写入.vnc/xstartup

# .vnc/xstartup 在最后一行追加
startxfce4 &

4. 启动vncserver

vncserver :1

5. Windows ssh linux 5901端口隧穿

# Windows, 这里改为你自己的linux服务器
ssh <username>@<vnsserverip>  -C  -L 5901:127.0.0.1:5901

6. Windows安装tigervnc (我这里使用scoop)

scoop install tigervnc
# 找到vncviewer.exe

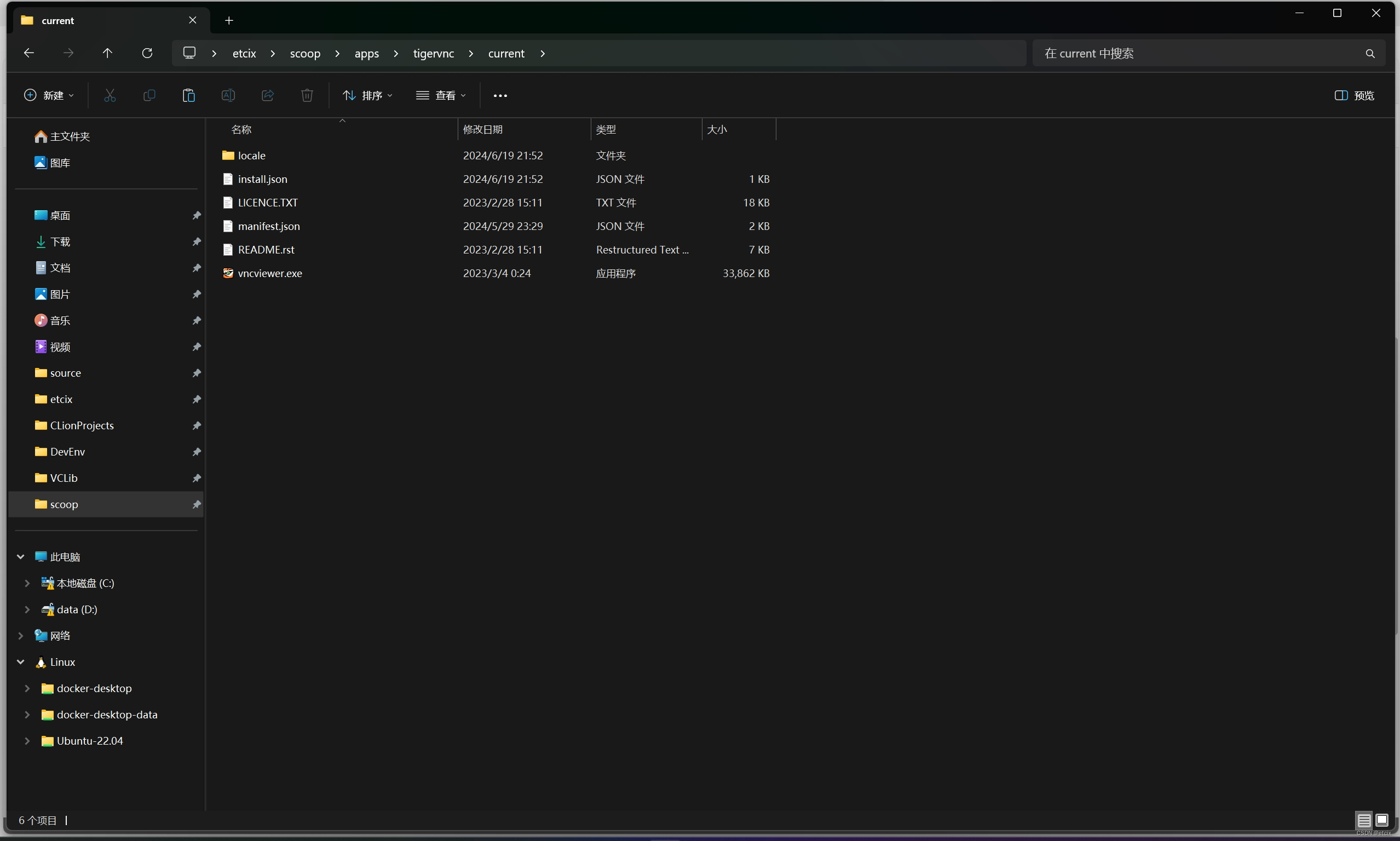
在这里插入图片描述

7. Windows连接, localhost:5901

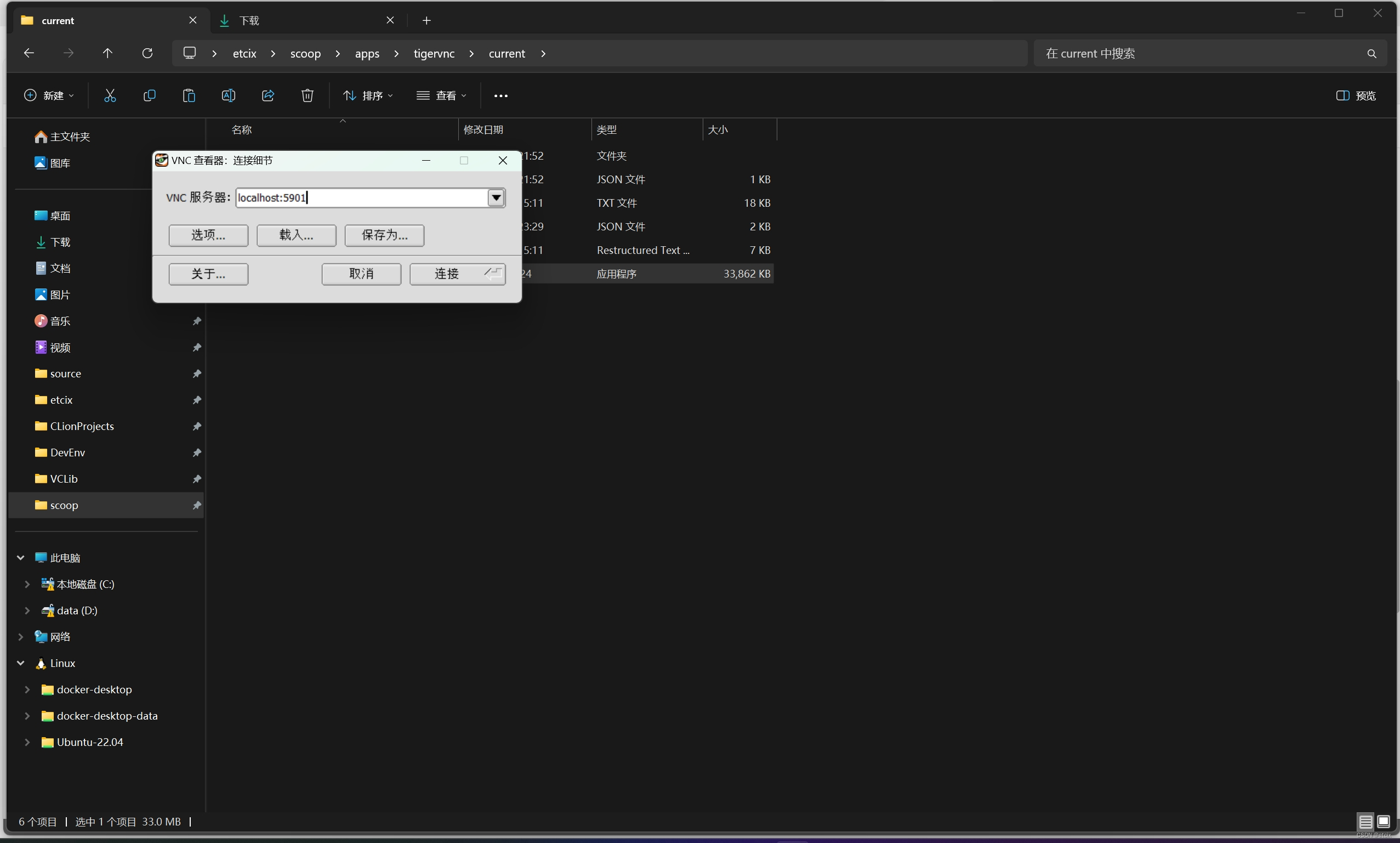
在这里插入图片描述

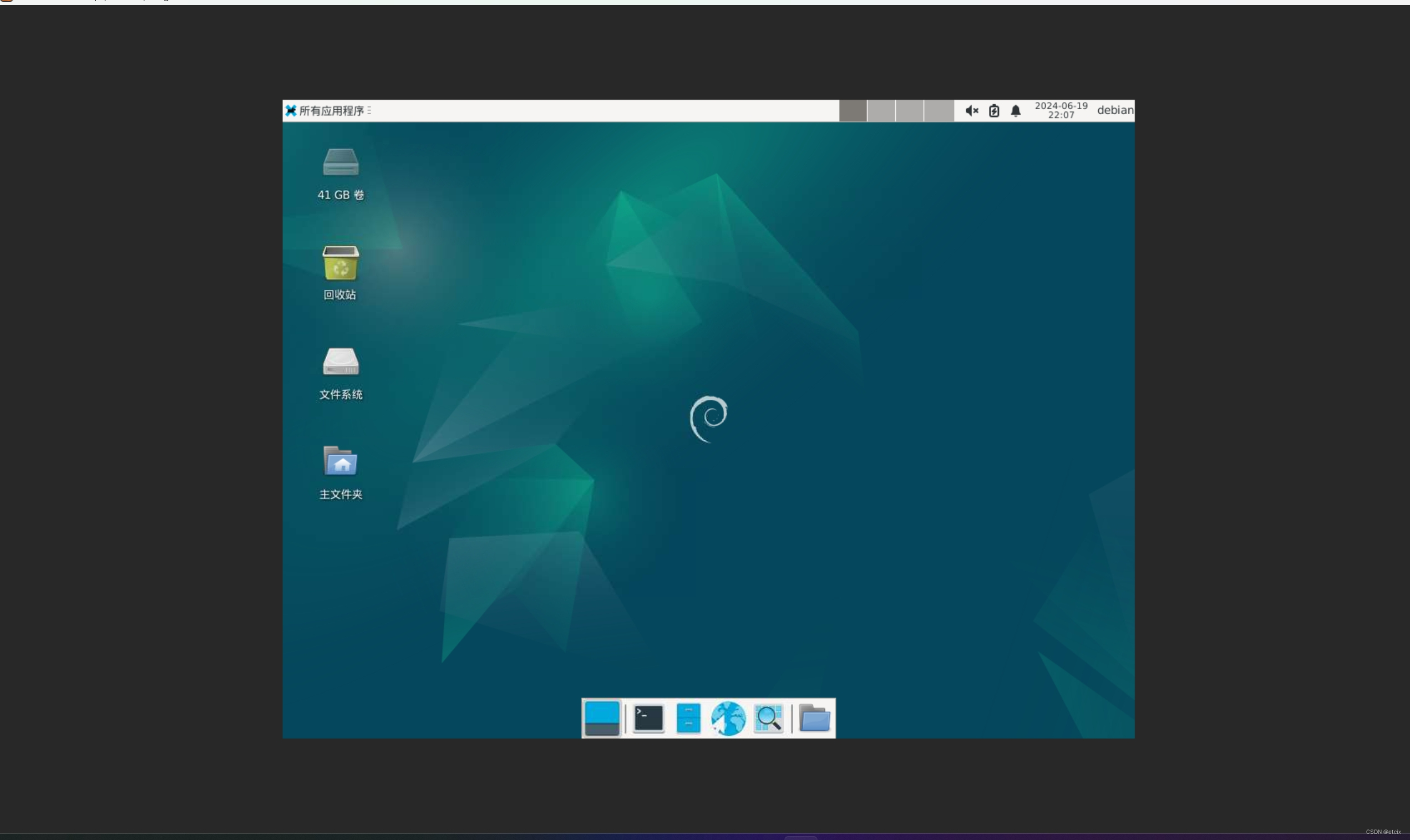
8. 输入vncserver配置的密码 登录linux图形界面, 你试试看

在这里插入图片描述

相关文章：

linux配置Vnc Server给Windows连接

1. linux 安装必要vnc server和桌面组件 sudo apt -y install tightvncserversudo apt install xfce4 xfce4-goodies2. linux 配置vncserver密码 #bash vncserver参考: https://cn.linux-console.net/?p21846#google_vignette 3. 将启动桌面命令写入.vnc/xstartup # .vnc/x…...

编程日记 2024/6/20 6:55:19

Android中的KeyEvent详解

介绍 在Android中&#xff0c;KeyEvent 是用来表示按键事件的类&#xff0c;可根据对应的事件来处理按键输入&#xff0c;具体包含了关于按键事件的信息&#xff0c;例如按键的代码、动作&#xff08;按下或释放&#xff09;以及事件的时间戳&#xff0c;KeyEvent 对象通常在用…...

编程日记 2024/6/20 6:52:15

移植案例与原理 - HDF驱动框架-驱动配置（2）

1.2.7 节点复制 节点复制可以实现在节点定义时从另一个节点先复制内容&#xff0c;用于定义内容相似的节点。语法如下&#xff0c;表示在定义"node"节点时将另一个节点"source_node"的属性复制过来。 node : source_node示例如下&#xff0c;编译后bar节点…...

编程日记 2024/6/20 6:51:14

年终奖发放没几天，提离职领导指责我不厚道，我该怎么办？

“年终奖都发了&#xff0c;你还跳槽&#xff1f;太不厚道了吧&#xff01;” “拿完年终奖就走人&#xff0c;这不是典型的‘骑驴找马’吗&#xff1f;” 每到岁末年初&#xff0c;关于“拿到年终奖后是否应该立即辞职”的话题总会引发热议。支持者认为&#xff0c;这是个人…...

编程日记 2024/6/20 6:49:11

多处理系统结构

目录 统一内存访问&#xff08;UMA&#xff09;多处理器系统结构 优点 缺点 应用场景 UMA 结构的架构示例 解决方案和改进 非统一内存访问&#xff08;NUMA&#xff09;多处理系统结构 概述 NUMA的优点 NUMA的缺点 NUMA系统的工作原理 NUMA优化策略 结论 现代计算…...

编程日记 2024/6/20 6:48:09

创建进程的常用方式

自学python如何成为大佬(目录):https://blog.csdn.net/weixin_67859959/article/details/139049996?spm1001.2014.3001.5501 在Python中有多个模块可以创建进程&#xff0c;比较常用的有os.fork()函数、multiprocessing模块和Pool进程池。由于os.fork()函数只适用于Unix/Linu…...

编程日记 2024/6/20 6:46:07

李宏毅2023机器学习作业HW06解析和代码分享

ML2023Spring - HW6 相关信息&#xff1a; 课程主页 课程视频 Sample code HW06 视频 HW06 PDF 个人完整代码分享: GitHub | Gitee | GitCode P.S. HW06 是在 Judgeboi 上提交的&#xff0c;出于学习目的这里会自定义两个度量的函数&#xff0c;不用深究&#xff0c;遵循 Sugge…...

编程日记 2024/6/20 6:44:03

专业技能篇--算法

文章目录 前言经典算法思想总结一、贪心算法二、动态规划三、回溯算法四、分治算法 前言 这篇简单理解一些常见的算法。如果面试的时候问到相关的算法&#xff0c;能够应付一二。 经典算法思想总结 一、贪心算法 思想&#xff1a;贪心算法是一种在每一步选择中都采取在当前状…...

编程日记 2024/6/20 6:42:01

Vue中CSS动态样式绑定

Vue中CSS动态样式绑定与注意事项_vue css动态绑定-CSDN博客 在 Vue 中&#xff0c;你不能直接在 CSS 中直接绑定 data 中的数据&#xff0c;因为 CSS 不是响应式的。但是&#xff0c;有几种方法可以实现根据 Vue 实例中的数据来动态地改变样式&#xff1a; 内联样式绑定&…...

编程日记 2024/6/20 6:40:59

【漏洞复现】契约锁电子签章平台 add 远程命令执行漏洞(XVE-2023-23720)

0x01 产品简介 契约锁电子签章平台是上海亘岩网络科技有限公司推出的一套数字签章解决方案。契约锁为中大型组织提供“数字身份、电子签章、印章管控以及数据存证服务”于一体的数字可信基础解决方案,可无缝集成各类系统,让其具有电子化签署的能力,实现组织全程数字化办公。通…...

编程日记 2024/6/20 6:39:56

计算机专业是否仍是“万金油”？

身份角度一&#xff1a;一名曾经的计算机专业学生  随着高考的结束&#xff0c;我站在了人生的分岔路口&#xff0c;面临着大学专业的选择。在众多的选择中&#xff0c;计算机专业一直是我深思熟虑后的一个重要选项。然而&#xff0c;我并不清楚自己是否真的适合这个专业&…...

编程日记 2024/6/20 6:37:50

Spring 启动顺序

在 Spring 框架中&#xff0c;应用启动过程涉及多个步骤和组件的初始化。理解 Spring 启动顺序不仅有助于优化应用性能&#xff0c;还能帮助开发人员排查启动过程中可能出现的问题。本文将详细介绍 Spring 启动过程中的关键步骤和顺序。 1. Spring 启动过程概述 Spring 应用的…...

编程日记 2024/6/20 6:36:48

2024.06.19 刷题日记

41. 缺失的第一个正数 这个题目的通过率很低&#xff0c;是一道难题&#xff0c;类似于脑筋急转弯&#xff0c;确实不好想。实际上&#xff0c;对于一个长度为 N 的数组&#xff0c;其中没有出现的最小正整数只能在 [1,N1] 中。 这个结论并不好想&#xff0c;举个例子&#x…...

编程日记 2024/6/20 6:35:46

linux系统中，pwd获取当前路径，dirname获取上一层路径；不使用 ../获取上一层路径

在实际项目中&#xff0c;我们通常可以使用 pwd 来获取当前路径&#xff0c;但是如果需要获取上一层路径&#xff0c;有不想使用 …/ 的方式&#xff0c;可以尝试使用 dirname指令 测试shell脚本 #!/bin/bash# 获取当前路径 CURRENT_PATH$PWD echo "CURRENT_PATH$CURREN…...

编程日记 2024/6/20 6:34:45

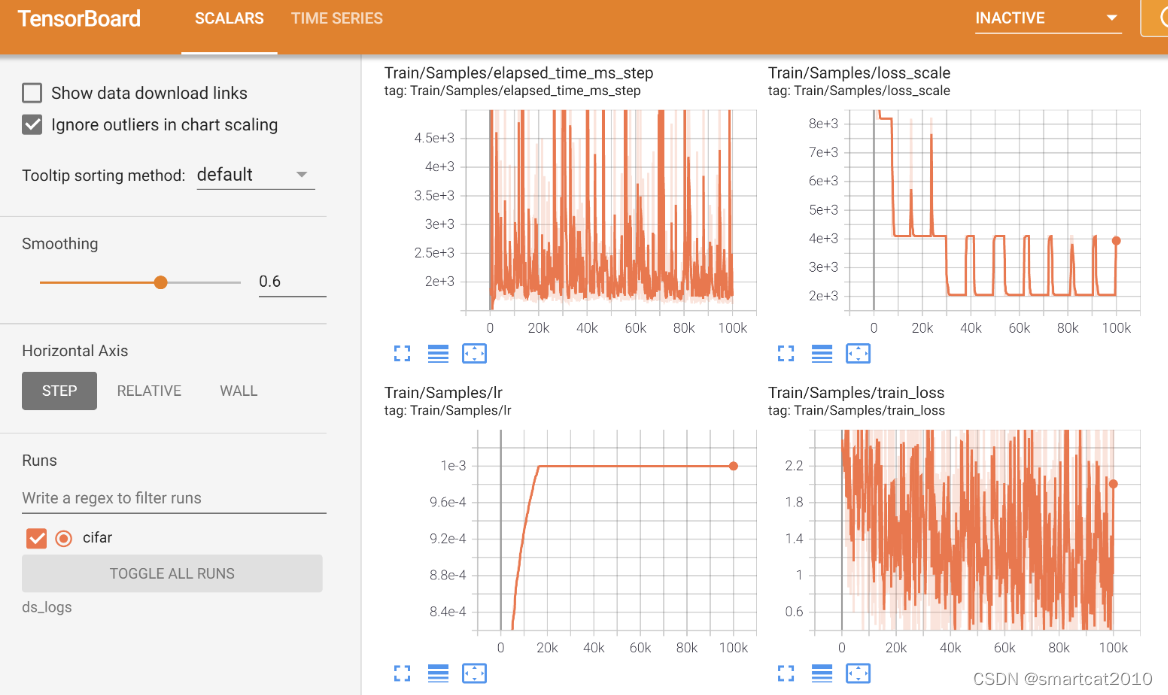
DeepSpeed Monitoring Comm. Logging

Monitoring 支持多种后端&#xff1a;Tensorboard、WandB、Comet、CSV文件&#xff1b; TensorBoard例子&#xff1a; 自动监控&#xff1a;DeepSpeed自动把重要metric记录下来。只需在配置文件里enable相应的看板后端即可&#xff1a; {"tensorboard": {"enabl…...

编程日记 2024/6/20 6:33:43

关于INCA的几个实用功能

01--VUI窗口设计 这个可以按照自己的想法设计INCA观测或标定窗口 首先进入到INCA的环境内&#xff0c;点击实验→加载VUI窗口 选择空的窗口 打开后如下所示&#xff1a; 点击UI开发模式&#xff0c;如下图 如下&#xff1a; 添加标定量、观测量、示波器 窗口的大小需要在开发…...

编程日记 2024/6/20 6:32:42

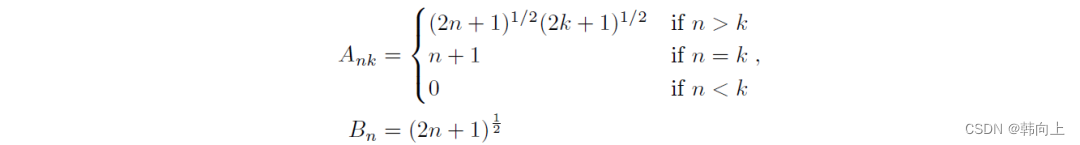
Mamaba3--RNN、状态方程、勒让德多项式

Mamaba3–RNN、状态方程、勒让德多项式 一、简单回顾 在Mamba1和Mamba2中分别介绍了RNN和状态方程。 下面从两个图和两个公式出发&#xff0c;对RNN和状态方程做简单的回顾&#xff1a; R N N : s t W s t − 1 U x t &#xff1b; O t V s t RNN: s_t Ws_{t-1}Ux_t&…...

编程日记 2024/6/20 6:31:40

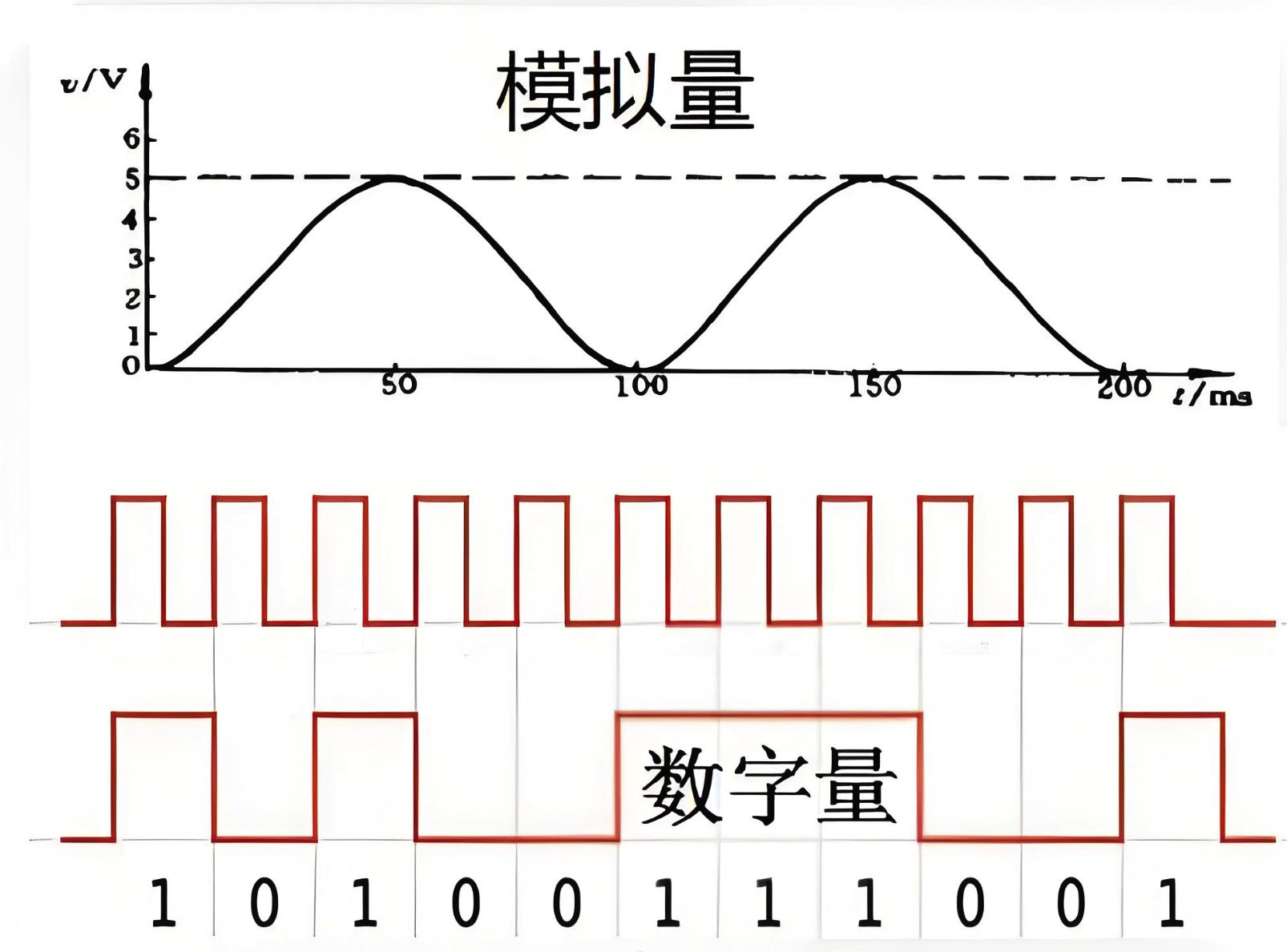
PLC模拟量和数字量到底有什么区别?

PLC模拟量和数字量的区别 在工业自动化领域&#xff0c;可编程逻辑控制器&#xff08;PLC&#xff09;是控制各种机械设备和生产过程的核心组件。PLC通过处理模拟量和数字量来实现对工业过程的精确控制。了解模拟量和数字量的区别对于设计高效、可靠的自动化系统至关重要。 1. …...

编程日记 2024/6/20 6:28:37

html中如何写一个提示框,css画一个提示框

在HTML中&#xff0c;提示框通常使用<div>元素来创建&#xff0c;然后使用CSS进行样式化。以下是一个示例&#xff0c;展示如何在HTML中写一个提示框&#xff0c;并使用CSS来设计其外观。 HTML 首先&#xff0c;创建一个HTML文件&#xff0c;其中包含一个提示框的结构&…...

编程日记 2024/6/20 6:25:32

ExoPlayer 学习笔记

https://www.51cto.com/article/777840.html ExoPlayer支持多种媒体格式和流媒体协议的播放器 播放视频&#xff1a;player.play()暂停视频&#xff1a;player.pause()停止播放&#xff1a;player.stop() Media3 ExoPlayer | Android media | Android Developers implem…...

编程日记 2024/6/20 6:23:30

【大模型RAG】拍照搜题技术架构速览：三层管道、两级检索、兜底大模型

摘要 拍照搜题系统采用“三层管道&#xff08;多模态 OCR → 语义检索 → 答案渲染&#xff09;、两级检索&#xff08;倒排 BM25 向量 HNSW&#xff09;并以大语言模型兜底”的整体框架&#xff1a; 多模态 OCR 层 将题目图片经过超分、去噪、倾斜校正后&#xff0c;分别用…...

编程新知 2026/2/10 23:40:16

React 第五十五节 Router 中 useAsyncError的使用详解

前言 useAsyncError 是 React Router v6.4 引入的一个钩子&#xff0c;用于处理异步操作&#xff08;如数据加载&#xff09;中的错误。下面我将详细解释其用途并提供代码示例。 一、useAsyncError 用途 处理异步错误&#xff1a;捕获在 loader 或 action 中发生的异步错误替…...

编程新知 2025/11/25 10:36:53

基于服务器使用 apt 安装、配置 Nginx

&#x1f9fe; 一、查看可安装的 Nginx 版本 首先&#xff0c;你可以运行以下命令查看可用版本&#xff1a; apt-cache madison nginx-core输出示例&#xff1a; nginx-core | 1.18.0-6ubuntu14.6 | http://archive.ubuntu.com/ubuntu focal-updates/main amd64 Packages ng…...

编程新知 2026/1/9 12:53:59

系统设计 --- MongoDB亿级数据查询优化策略

系统设计 --- MongoDB亿级数据查询分表策略 背景Solution --- 分表 背景 使用audit log实现Audi Trail功能 Audit Trail范围: 六个月数据量: 每秒5-7条audi log&#xff0c;共计7千万 – 1亿条数据需要实现全文检索按照时间倒序因为license问题&#xff0c;不能使用ELK只能使用…...

编程新知 2026/1/4 3:47:09

【Zephyr 系列 10】实战项目：打造一个蓝牙传感器终端 + 网关系统（完整架构与全栈实现）

🧠关键词：Zephyr、BLE、终端、网关、广播、连接、传感器、数据采集、低功耗、系统集成 📌目标读者：希望基于 Zephyr 构建 BLE 系统架构、实现终端与网关协作、具备产品交付能力的开发者 📊篇幅字数：约 5200 字 ✨ 项目总览 在物联网实际项目中，**“终端 + 网关”**是…...

编程新知 2026/1/31 6:12:22

高效线程安全的单例模式：Python 中的懒加载与自定义初始化参数

高效线程安全的单例模式：Python 中的懒加载与自定义初始化参数 在软件开发中，单例模式（Singleton Pattern）是一种常见的设计模式，确保一个类仅有一个实例，并提供一个全局访问点。在多线程环境下，实现单例模式时需要注意线程安全问题，以防止多个线程同时创建实例，导致…...

编程新知 2025/11/25 19:50:27

HubSpot推出与ChatGPT的深度集成引发兴奋与担忧

上周三&#xff0c;HubSpot宣布已构建与ChatGPT的深度集成&#xff0c;这一消息在HubSpot用户和营销技术观察者中引发了极大的兴奋&#xff0c;但同时也存在一些关于数据安全的担忧。 许多网络声音声称&#xff0c;这对SaaS应用程序和人工智能而言是一场范式转变。 但向任何技…...

编程新知 2026/2/6 4:24:06

django blank 与 null的区别

1.blank blank控制表单验证时是否允许字段为空 2.null null控制数据库层面是否为空 但是&#xff0c;要注意以下几点&#xff1a; Django的表单验证与null无关&#xff1a;null参数控制的是数据库层面字段是否可以为NULL&#xff0c;而blank参数控制的是Django表单验证时字…...

编程新知 2025/7/7 3:34:13

Sklearn 机器学习 缺失值处理 获取填充失值的统计值

💖亲爱的技术爱好者们，热烈欢迎来到 Kant2048 的博客！我是 Thomas Kant，很开心能在CSDN上与你们相遇～💖 本博客的精华专栏： 【自动化测试】 【测试经验】 【人工智能】 【Python】 使用 Scikit-learn 处理缺失值并提取填充统计信息的完整指南 在机器学习项目中，数据清…...

编程新知 2026/1/20 10:06:51

全面解析数据库：从基础概念到前沿应用​

在数字化时代&#xff0c;数据已成为企业和社会发展的核心资产&#xff0c;而数据库作为存储、管理和处理数据的关键工具&#xff0c;在各个领域发挥着举足轻重的作用。从电商平台的商品信息管理&#xff0c;到社交网络的用户数据存储&#xff0c;再到金融行业的交易记录处理&a…...

编程新知 2025/9/19 11:48:17