一种基于非线性滤波过程的旋转机械故障诊断方法(MATLAB)
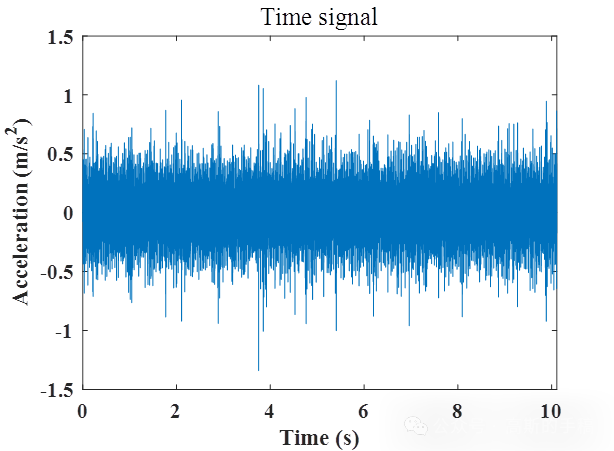
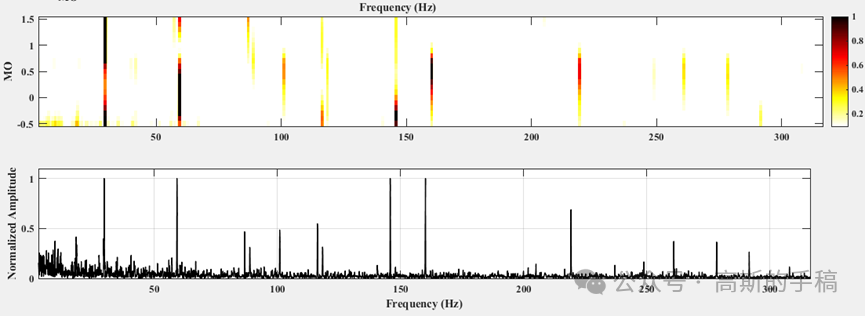
在众多的旋转机械故障诊断方法中,包络分析,又称为共振解调技术,是目前应用最为成功的方法之一。首先,对激励引起的共振频带进行带通滤波,然后对滤波信号进行包络谱分析,通过识别包络谱中的故障相关的特征频率,从而判断是否发生故障与故障的类型。然而,包络分析方法的主要难点在于共振频带的选取。为了解决这一难题,基于谱峭度的峭度图方法被提出,通过计算由STFT或者有限脉冲滤波器得到的窄带包络信号的峭度,确定信号中非高斯成分所在的频带。随着研究的深入,峭度图的缺点逐渐暴露。峭度指标不能区分冲击是否由循环冲击引起,因此,在两种情况下容易失效。第一种是存在较强的脉冲噪声时,第二种是故障脉冲重复频率较高时。
为了解决这一问题,众多学者提出了一系列的改进方法,例如:improvedKurto⁃gram,enhancedKurtogram,Protrugram,Info⁃gram,Autogram均取得了不错的效果。一些基于周期指标的峭度图被提出来,可以用来寻找具有指定周期成分所在的频带,极大地降低了背景噪声的影响。但是这类方法需要预知精确的故障周期,缺乏自适应性。到目前为止,找到最佳的解调频带依然不是一个简单的任务。峭度图方法寻找到的频带仅能识别一个最佳频带,由于缺陷产生的冲击会在不同的频率范围内激发机器结构产生共振,仅从一个频带恢复原信号,会丢失很多故障信息。尤其当信号中存在多个故障时,弱故障往往不能被识别,因此,需要对信号进行多频段滤波,才能完全提取出缺陷信号。
鉴于此,有大佬提出了一种新的非线性滤波的方法去分离信号,首先对振动信号进行傅里叶变换获得频域幅值谱和相位谱,通过对其幅值谱赋予不同权重的指数,并结合原始信号相位谱进行逆傅里叶变换,从而获得一系列的修正信号,最后通过修正信号平方包络的功率谱识别故障特征。该方法计算简单、效率高、自适应强,且摆脱了对评价指标的依赖,取得了显著的效果。
function Ren=renyi_entropy(TFR,t,f,alpha)
% Ren=renyi_entropy(TFR,t,f,alpha) calculates Renyi entropy from 2-D TFR
%
% Inputs:
% TFR : (M,N) 2-D TFR function.
% T : a time vector (default : (1:N)).
% F : a frequency vector (default : (1:M)).
% ALPHA : Renyi measure order (default : 3).
%
% Outputs:
% Ren=1/(1-ALPHA)*log2[Sum[TFR(Fi,Ti)^ALPHA dFi.dTi]]
% Fi,Ti : Alpha-order Renyi entropy
% ALPHA = 1: limit case, the outcomes will be Shannon entropy
% Sha = - Sum[TFR(Fi,Ti)log2[TFR(Fi,Ti)]dFi.dTi]
% Fi,Tiif (nargin == 0),error('At least one parameter required');
end;[M,N] = size(TFR);
if (nargin == 1),t=1:N; f=(1:M)'; alpha=3;
elseif (nargin == 2),f=(1:M)'; alpha=3;
elseif (nargin == 3),alpha=3;
end;f=sort(f); %sort frequency vector in ascending order such that the first
%row TFR must correspond to the lower frequenciesTFR = TFR./trapz(f,trapz(t,TFR,2));
% Normalisation TFR;
%trapz function is used to calculate 2D integral of %matrix TFR according
%to abscissa X and ordinate Yif alpha == 1 % limit case case: Shannon entropyif (min(min(TFR))<0)error('distribution with negative values => alpha=1 not allowed');elseRen=-trapz(f,trapz(t,TFR.*log2(TFR+eps),2));end
else % Renyi entropyRen=1/(1-alpha)*log2(trapz(f,trapz(t,TFR.^alpha,2))+eps);完整代码:https://mbd.pub/o/bread/mbd-ZJeYmJdv
end
相关文章:

一种基于非线性滤波过程的旋转机械故障诊断方法(MATLAB)
在众多的旋转机械故障诊断方法中,包络分析,又称为共振解调技术,是目前应用最为成功的方法之一。首先,对激励引起的共振频带进行带通滤波,然后对滤波信号进行包络谱分析,通过识别包络谱中的故障相关的特征频…...

HarmonyOS Next 系列之从手机选择图片或拍照上传功能实现(五)
系列文章目录 HarmonyOS Next 系列之省市区弹窗选择器实现(一) HarmonyOS Next 系列之验证码输入组件实现(二) HarmonyOS Next 系列之底部标签栏TabBar实现(三) HarmonyOS Next 系列之HTTP请求封装和Token…...

如果xml在mapper目录下,如何扫描到xml
如果xml在mapper目录下,如何扫描到xml 项目结构 src├── main│ ├── java│ │ └── com│ │ └── bg│ │ ├── Application.java│ │ ├── domain│ │ │ └── User.java│ │ …...
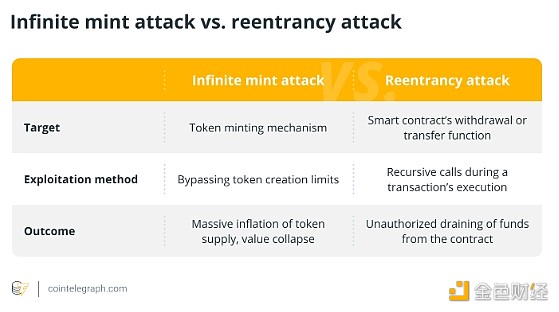
什么是无限铸币攻击?它是如何运作的?
一、无限铸币攻击解释 无限铸币攻击是指攻击者操纵合约代码不断铸造超出授权供应限制的新代币。 这种黑客行为在去中心化金融 (DeFi) 协议中最为常见。这种攻击通过创建无限数量的代币来损害加密货币或代币的完整性和价值。 例如,一名黑客利用了 Paid 网络的智能…...

【Android】怎么使APP进行开机启动
项目需求 在Android系统开启之后,目标app可以在系统开机之后启动。 项目实现 使用广播的方式 首先我们要创建一个广播(这里是启动了一个Service服务) public class BootReceiver extends BroadcastReceiver {Overridepublic void onReceive(Context context, I…...

详细分析Element Plus的el-pagination基本知识(附Demo)
目录 前言1. 基本知识2. Demo3. 实战 前言 需求:从无到有做一个分页并且附带分页的导入导出增删改查等功能 前提一定是要先有分页,作为全栈玩家,先在前端部署一个分页的列表 相关后续的功能,是Java,推荐阅读&#x…...

ubuntu换镜像源方法
查看ubuntu的版本,不同的版本对应的不同的镜像源 cat /etc/issue Ubuntu 18.04.6 LTS \n \l 先备份一个,防止更改错误 cobol cp /etc/apt/sources.list /etc/apt/sources.list.backup 先进入清华源,搜索ubuntu,点击问号 点进来可以看到可以…...

python flask配置邮箱发送功能,使用flask_mail模块
🌈所属专栏:【Flask】✨作者主页: Mr.Zwq✔️个人简介:一个正在努力学技术的Python领域创作者,擅长爬虫,逆向,全栈方向,专注基础和实战分享,欢迎咨询! 您的点…...

Flask快速入门(路由、CBV、请求和响应、session)
Flask快速入门(路由、CBV、请求和响应、session) 目录 Flask快速入门(路由、CBV、请求和响应、session)安装创建页面Debug模式快速使用Werkzeug介绍watchdog介绍快速体验 路由系统源码分析手动配置路由动态路由-转换器 Flask的CBV…...
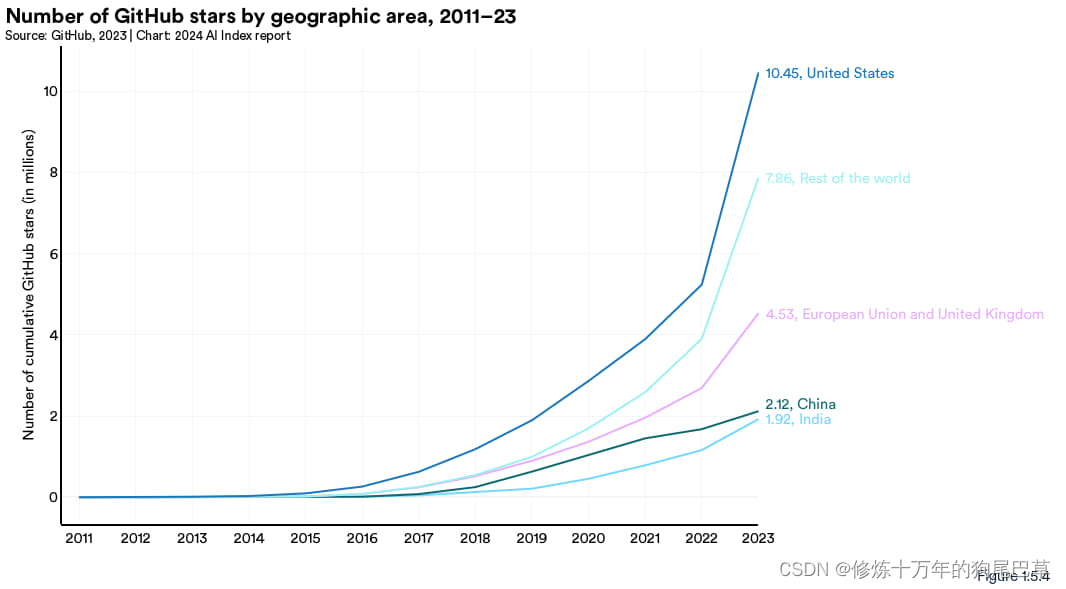
人工智能指数报告
2024人工智能指数报告(一):研发 前言 全面分析人工智能的发展现状。 从2017年开始,斯坦福大学人工智能研究所(HAI)每年都会发布一份人工智能的研究报告,人工智能指数报告(AII&…...
聊聊 Mybatis 动态 SQL
这篇文章,我们聊聊 Mybatis 动态 SQL ,以及我对于编程技巧的几点思考 ,希望对大家有所启发。 1 什么是 Mybatis 动态SQL 如果你使用过 JDBC 或其它类似的框架,你应该能理解根据不同条件拼接 SQL 语句有多痛苦,例如拼…...

【windows|004】BIOS 介绍及不同品牌电脑和服务器进入BIOS设置的方法
🍁博主简介: 🏅云计算领域优质创作者 🏅2022年CSDN新星计划python赛道第一名 🏅2022年CSDN原力计划优质作者 🏅阿里云ACE认证高级工程师 🏅阿里云开发者社区专家博主 💊交流社…...
lvgl的应用:移植MusicPlayer(基于STM32F407)
目录 概述 1 软硬件环境 1.1 UI开发版本 1.2 MCU开发环境 1.3 注意点 2 GUI Guider开发UI 2.1 使用GUI Guider创建UI 2.2 GUI Guider编译项目和测试 2.2.1 GUI Guider编译项目 2.2.2 编译 2.3 了解GUI Guider生成代码 3 移植项目 3.1 Keil中加载代码 3.2 调用G…...
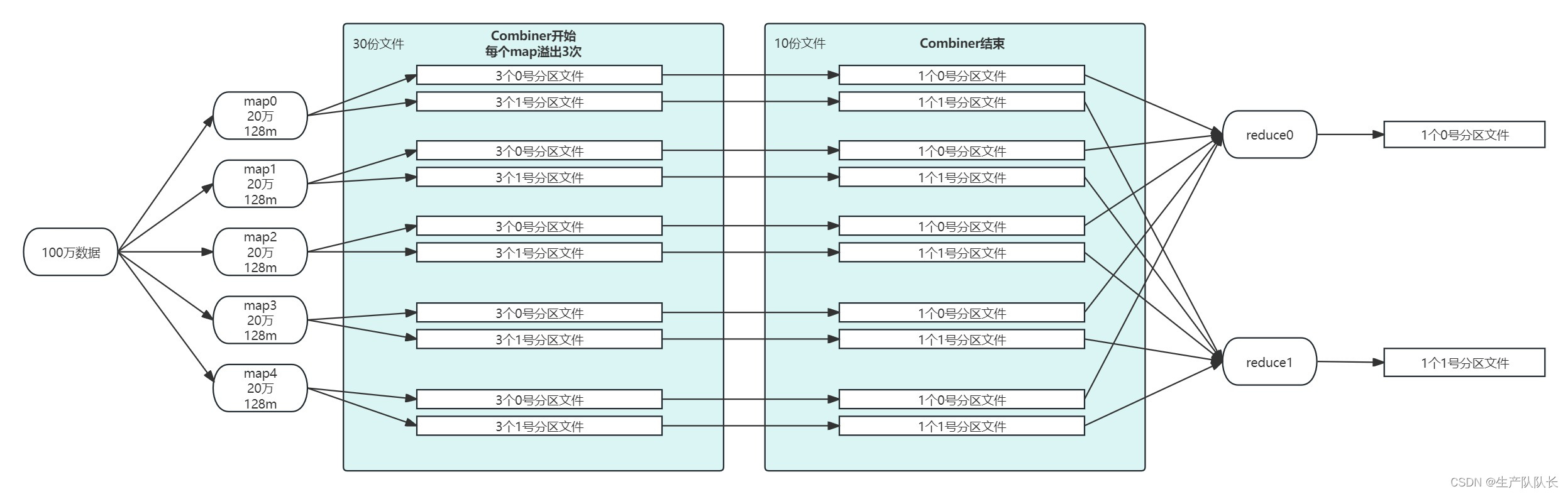
Hadoop3:MapReduce中的Shuffle机制
一、流程图 Shuffle是Map方法之后,Reduce方法之前的数据处理过程称。 二、图解说明 1、数据流向 map方法中context.write(outK, outV);开始,写入环形缓冲区,再进行分区排序,写到磁盘 reduce方法拉取磁盘上的数据,…...
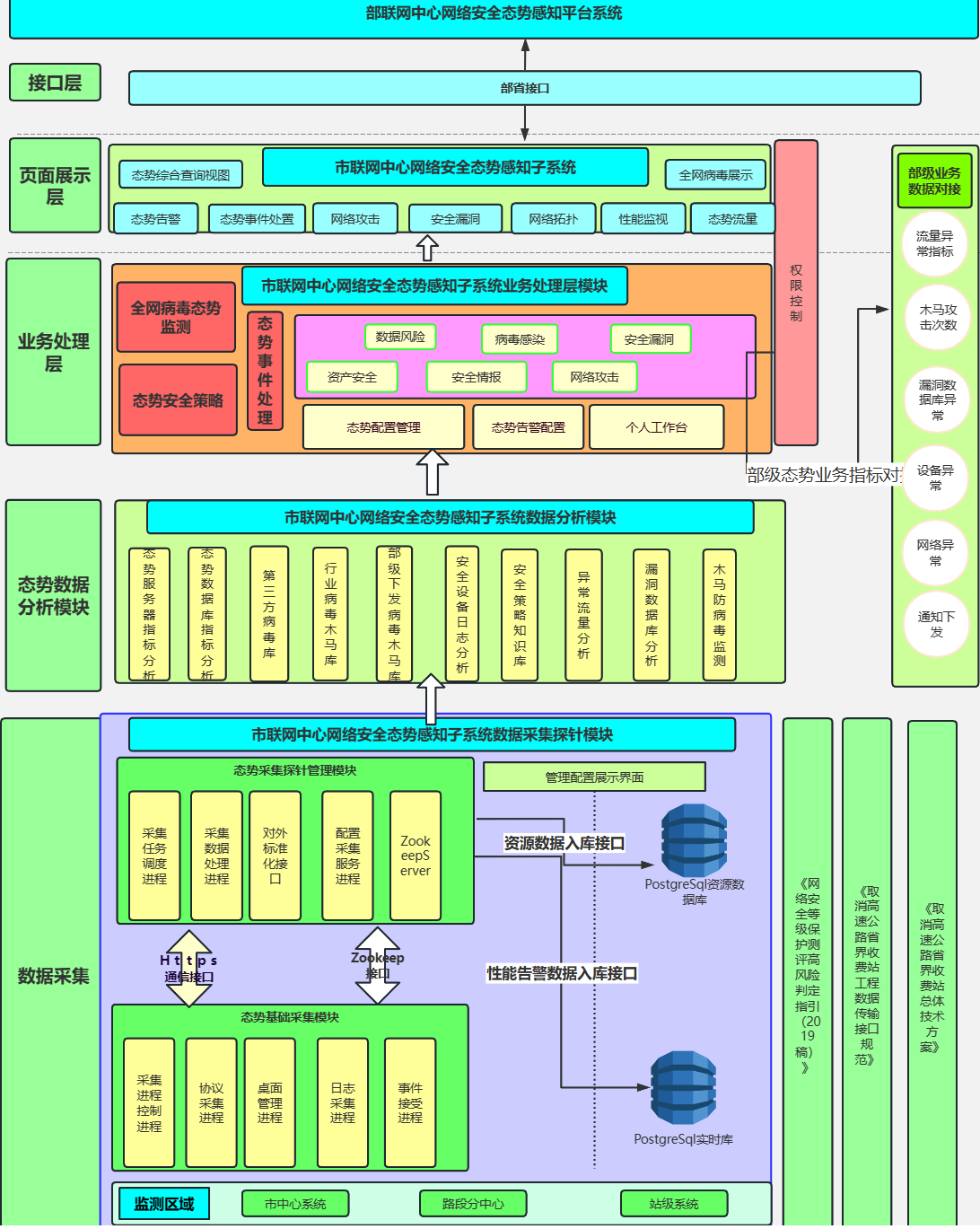
从设计到实践:高速公路监控技术架构全剖析
随着高速公路网络的迅速扩展和交通流量的日益增加,高效的监控系统成为保障交通安全、提升管理效率的重要手段。本文将深入探讨高速公路监控技术架构,从设计理念到实际应用,全面解析这一关键技术的各个环节。 ### 一、系统设计理念 #### 1. 高…...

Go Context
Context 介绍 Context 代表了协程的上下文,用以在父子协程之间传递控制信号,共享变量等操作// context.Context 接口 type Context interface {// 当Context自动取消或者到了取消时间被取消后返回Deadline() (deadline time.Time, ok bool)// 当Contex…...
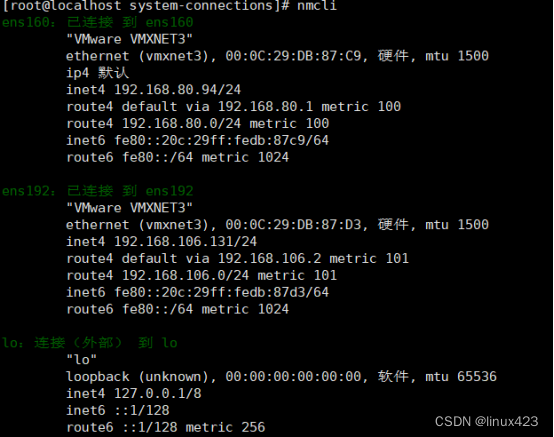
centOS Stream9配置NAT8网络
首先将VMware关机,添加网络适配器 启动虚拟机,查看ens192是否打开连接 安装的图形化需要查看右上角电源处网卡是否连接 最小化安装一般不会出现未连接的状态 使用ip a 查看 配置网卡文件 cd /etc/NetworkManager/system-connections/cd到当前目录下…...
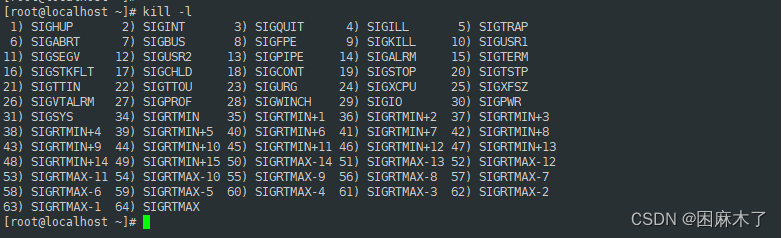
Linux - 进程
一、什么是进程 首先,Linux是一个多用户多进程的操作系统,系统上可以同时运行多个进程。 进程的产生:①是在执行程序或者命令时产生的;②定时任务进程 进程的类型:前台进程/后台进程 前台进程:一个终端…...
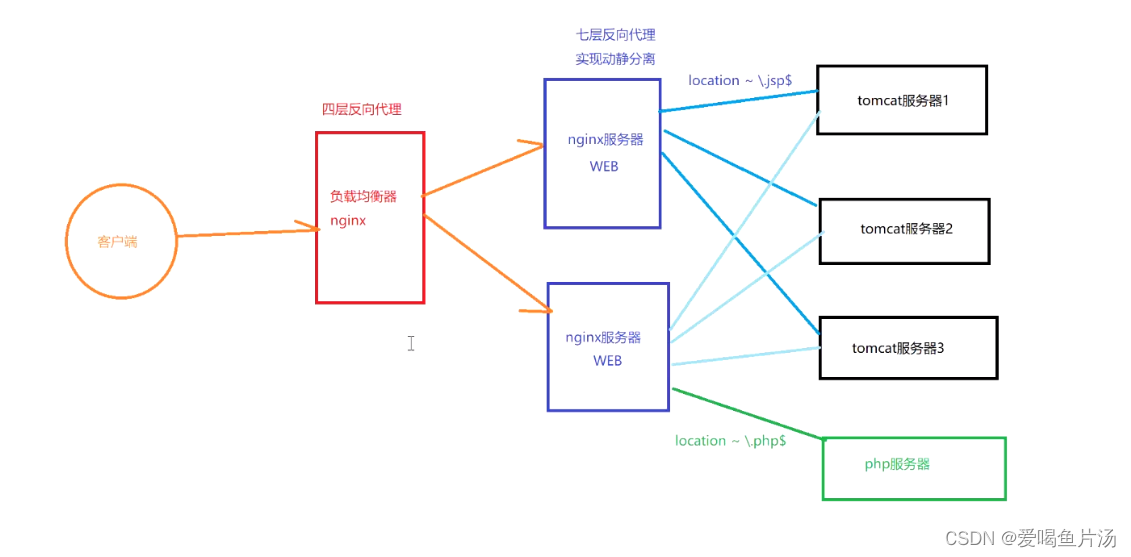
nginx+tomcat负载均衡、动静分离群集【☆☆☆☆☆】
Nginx是一款非常优秀的HTTP服务器软件,性能比tomcat更优秀,它支持高达50 000个并发连接数,拥有强大的静态资源处理能力,运行稳定,内存、CPU等系统资源消耗非常低。目前很多大型网站都应用Nginx服务器作为后端网站程序的…...

MySQL容器部署步骤
1、拉取MySQL镜像 docker pull mysql # 默认拉取最新版本docker pull mysql:5.7 # 拉取5.7版本docker pull mysql:8.0 # 拉取8.0版本 2、创建挂载目录 # 创建挂载目录 mkdir -p /home/mysql/conf/ # -p: 多级创建mkdir -p /home/mysql/log/mkdir -p /home/mysql/data/ 3…...

conda相比python好处
Conda 作为 Python 的环境和包管理工具,相比原生 Python 生态(如 pip 虚拟环境)有许多独特优势,尤其在多项目管理、依赖处理和跨平台兼容性等方面表现更优。以下是 Conda 的核心好处: 一、一站式环境管理:…...

Flask RESTful 示例
目录 1. 环境准备2. 安装依赖3. 修改main.py4. 运行应用5. API使用示例获取所有任务获取单个任务创建新任务更新任务删除任务 中文乱码问题: 下面创建一个简单的Flask RESTful API示例。首先,我们需要创建环境,安装必要的依赖,然后…...

Java如何权衡是使用无序的数组还是有序的数组
在 Java 中,选择有序数组还是无序数组取决于具体场景的性能需求与操作特点。以下是关键权衡因素及决策指南: ⚖️ 核心权衡维度 维度有序数组无序数组查询性能二分查找 O(log n) ✅线性扫描 O(n) ❌插入/删除需移位维护顺序 O(n) ❌直接操作尾部 O(1) ✅内存开销与无序数组相…...

【第二十一章 SDIO接口(SDIO)】
第二十一章 SDIO接口 目录 第二十一章 SDIO接口(SDIO) 1 SDIO 主要功能 2 SDIO 总线拓扑 3 SDIO 功能描述 3.1 SDIO 适配器 3.2 SDIOAHB 接口 4 卡功能描述 4.1 卡识别模式 4.2 卡复位 4.3 操作电压范围确认 4.4 卡识别过程 4.5 写数据块 4.6 读数据块 4.7 数据流…...

高等数学(下)题型笔记(八)空间解析几何与向量代数
目录 0 前言 1 向量的点乘 1.1 基本公式 1.2 例题 2 向量的叉乘 2.1 基础知识 2.2 例题 3 空间平面方程 3.1 基础知识 3.2 例题 4 空间直线方程 4.1 基础知识 4.2 例题 5 旋转曲面及其方程 5.1 基础知识 5.2 例题 6 空间曲面的法线与切平面 6.1 基础知识 6.2…...

NLP学习路线图(二十三):长短期记忆网络(LSTM)
在自然语言处理(NLP)领域,我们时刻面临着处理序列数据的核心挑战。无论是理解句子的结构、分析文本的情感,还是实现语言的翻译,都需要模型能够捕捉词语之间依时序产生的复杂依赖关系。传统的神经网络结构在处理这种序列依赖时显得力不从心,而循环神经网络(RNN) 曾被视为…...

CRMEB 框架中 PHP 上传扩展开发:涵盖本地上传及阿里云 OSS、腾讯云 COS、七牛云
目前已有本地上传、阿里云OSS上传、腾讯云COS上传、七牛云上传扩展 扩展入口文件 文件目录 crmeb\services\upload\Upload.php namespace crmeb\services\upload;use crmeb\basic\BaseManager; use think\facade\Config;/*** Class Upload* package crmeb\services\upload* …...
)
Angular微前端架构:Module Federation + ngx-build-plus (Webpack)
以下是一个完整的 Angular 微前端示例,其中使用的是 Module Federation 和 npx-build-plus 实现了主应用(Shell)与子应用(Remote)的集成。 🛠️ 项目结构 angular-mf/ ├── shell-app/ # 主应用&…...

10-Oracle 23 ai Vector Search 概述和参数
一、Oracle AI Vector Search 概述 企业和个人都在尝试各种AI,使用客户端或是内部自己搭建集成大模型的终端,加速与大型语言模型(LLM)的结合,同时使用检索增强生成(Retrieval Augmented Generation &#…...

视觉slam十四讲实践部分记录——ch2、ch3
ch2 一、使用g++编译.cpp为可执行文件并运行(P30) g++ helloSLAM.cpp ./a.out运行 二、使用cmake编译 mkdir build cd build cmake .. makeCMakeCache.txt 文件仍然指向旧的目录。这表明在源代码目录中可能还存在旧的 CMakeCache.txt 文件,或者在构建过程中仍然引用了旧的路…...
