【机器学习】:线性回归模型学习路线
Hi~!这里是奋斗的小羊,很荣幸您能阅读我的文章,诚请评论指点,欢迎欢迎 ~~
💥💥个人主页:奋斗的小羊
💥💥所属专栏:C语言
🚀本系列文章为个人学习笔记,在这里撰写成文一为巩固知识,二为展示我的学习过程及理解。文笔、排版拙劣,望见谅。
目录
- 初识线性回归模型
- 学习必备数学知识
- 掌握数据预处理技巧
- 学习模型训练过程
- 掌握模型评估指标
- 1. 初识线性回归模型
- 2. 学习必备数学知识
- 3. 掌握数据预处理技巧
- 4. 学习模型评估指标
- 5. 深入理解模型训练过程
- 6. 掌握模型调参技巧

初识线性回归模型
线性回归模型是一种用于建立自变量与因变量之间线性关系的模型。例如,在房价预测问题中,我们可以使用线性回归模型来预测房屋价格与房屋面积之间的关系。
import numpy as np
from sklearn.linear_model import LinearRegression# 创建示例数据
X = np.array([[1], [2], [3], [4]])
y = np.array([2, 4, 6, 8])# 构建线性回归模型
model = LinearRegression()
model.fit(X, y)# 预测房屋价格
new_X = np.array([[5]])
predicted_price = model.predict(new_X)
print("预测房屋价格:", predicted_price)
学习必备数学知识
在学习线性回归模型时,深入理解相关数学知识非常重要。例如,我们需要了解线性代数中的矩阵运算,微积分中的梯度下降算法等。
import numpy as np# 矩阵乘法示例
A = np.array([[1, 2], [3, 4]])
B = np.array([[5], [6]])
result = np.dot(A, B)
print("矩阵相乘结果:", result)
掌握数据预处理技巧
在实际应用中,数据预处理是机器学习的重要一步。例如,在预测学生考试成绩问题中,我们需要对数据进行缺失值处理和特征缩放等预处理操作。
import pandas as pd
from sklearn.preprocessing import StandardScaler# 读取数据
data = pd.read_csv("student_scores.csv")# 处理缺失值
data.fillna(data.mean(), inplace=True)# 特征缩放
scaler = StandardScaler()
data['score'] = scaler.fit_transform(data['score'].values.reshape(-1, 1))
学习模型训练过程
了解线性回归模型的训练过程对于深入理解模型至关重要。我们可以通过简单的例子来展示模型参数的更新过程。
import numpy as np# 示例数据
X_train = np.array([[1], [2], [3]])
y_train = np.array([2, 4, 6])# 初始参数
w = 0
b = 0
lr = 0.01# 模型训练过程
for i in range(100):y_pred = w * X_train + berror = y_pred - y_trainw -= lr * np.mean(error * X_train)b -= lr * np.mean(error)print("训练后的参数 w 和 b 分别为:", w, b)
掌握模型评估指标
评估模型性能是优化模型的关键步骤。例如,在线性回归模型中,我们可以使用均方误差(MSE)来评估模型的预测效果。
from sklearn.metrics import mean_squared_error# 计算均方误差
y_true = [3, -0.5, 2, 7]
y_pred = [2.5, 0.0, 2, 8]
mse = mean_squared_error(y_true, y_pred)
print("均方误差:", mse)
通过以上例子,我们可以深入学习线性回归模型的原理、应用和优化方法。希# 机器学习:线性回归模型学习路线
在机器学习领域,线性回归模型是一种用于建模自变量与因变量之间线性关系的常见模型。通过线性回归,我们可以预测连续型的因变量,例如房价、销售额等。接下来将详细介绍学习线性回归模型的路线,并结合实际例子进行解释。
1. 初识线性回归模型
线性回归模型的基本原理是利用自变量的线性组合来预测因变量。例如,考虑以下简单的线性回归方程:
y = m x + b y = mx + b y=mx+b
其中, y y y 是因变量, x x x 是自变量, m m m 是斜率, b b b 是截距。
例子: 假设我们有一组房屋的面积和价格数据,我们可以使用线性回归模型来预测房屋价格与面积之间的关系。
2. 学习必备数学知识
在理解线性回归模型时,我们需要掌握一些基础的数学知识,如线性代数和微积分。线性代数可以帮助我们理解特征之间的关系,微积分则有助于优化模型参数。
例子: 在线性代数中,我们可以使用矩阵运算来表示线性回归模型中的参数估计过程。例如,最小二乘法可以用矩阵形式表示为 β = ( X T X ) − 1 X T y β = (X^TX)^{-1}X^Ty β=(XTX)−1XTy。
3. 掌握数据预处理技巧
在应用线性回归模型之前,我们需要对数据进行预处理,以确保数据的质量和可靠性。
例子: 数据清洗阶段,我们可以处理异常值,填补缺失值等。例如,在房价预测中,我们可能需要处理一些缺失的房屋信息。
4. 学习模型评估指标
了解模型评估指标有助于评价模型的性能和准确性。
例子: 对于线性回归模型,我们可以使用均方误差(Mean Squared Error,MSE)来评估模型的预测效果。例如,MSE 越小,说明模型拟合得越好。
5. 深入理解模型训练过程
学习模型训练过程是提高模型性能的关键一步,需要了解梯度下降等优化算法。
例子: 在梯度下降算法中,我们根据损失函数的梯度更新模型参数,直到收敛于最优解。这可以帮助我们找到最优的模型参数来拟合数据。
6. 掌握模型调参技巧
调参是优化模型性能的重要一环,包括选择合适的正则化项、调整学习率等。
例子: 在正则化中,我们可以通过调整正则化参数来控制模型的复杂度,避免过拟合。
通过以上学习路线,结合大量实际例子,我们可以全面掌握线性回归模型的原理、应用和优化方法,从而在实际问题中灵活运用机器学习技术。希望以上内容对你学习线性回归模型有所帮助!
相关文章:

【机器学习】:线性回归模型学习路线
Hi~!这里是奋斗的小羊,很荣幸您能阅读我的文章,诚请评论指点,欢迎欢迎 ~~ 💥💥个人主页:奋斗的小羊 💥💥所属专栏:C语言 🚀本系列文章为个人学习…...
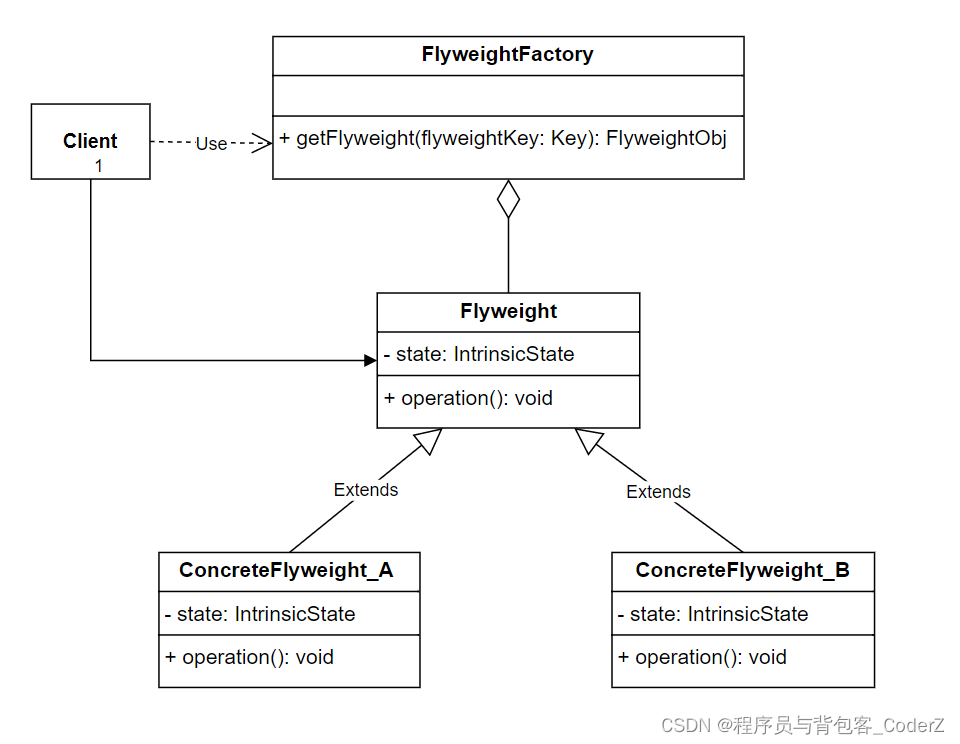
C++设计模式——Flyweight享元模式
一,享元模式简介 享元模式是一种结构型设计模式,它将每个对象中各自保存一份数据的方式改为多个对象共享同一份数据,该模式可以有效减少应用程序的内存占用。 享元模式的核心思想是共享和复用,通过设置共享资源来避免创建过多的实…...

Github 2024-06-19 开源项目日报 Top10
根据Github Trendings的统计,今日(2024-06-19统计)共有10个项目上榜。根据开发语言中项目的数量,汇总情况如下: 开发语言项目数量TypeScript项目3Rust项目2Go项目2JavaScript项目1Python项目1Dart项目1非开发语言项目1Ruby项目1HTML项目1项目化学习 创建周期:2538 天协议类…...

【ARM】如何通过Keil MDK查看芯片的硬件信息
【更多软件使用问题请点击亿道电子官方网站】 1、文档目标: 解决在开发过程中对于开发项目所使用的的芯片的参数查看的问题 2、问题场景: 在项目开发过程中,经常需要对于芯片的时钟、寄存器或者一些硬件参数需要进行确认。大多数情况下是需…...
elasticsearch的安装和配置
单节点安装与部署 我们通过docker进行安装 1.docker的安装 如果以及安装了docker就可以跳过这个步骤。 首先更新yum: yum update安装docker: yum install docker查看docker的版本: docker -v此时我们的docker就安装成功了。 2.创建网络 我们还需要部署kiban…...
华为云下Ubuntu20.04中Docker的部署
我想用Docker拉取splash,Docker目前已经无法使用(镜像都在国外)。这导致了 docker pull 命令的失败,原因是timeout。所以我们有必要将docker的源设置在国内,直接用国内的镜像。 1.在华为云下的Ubuntu20.04因为源的原因…...

1、C++编程中的基本运算 - 课件
一、基础知识 1、C程序的基本框架 // 预处理器指令,引入需要的头文件 #include <iostream> // 使用标准命名空间 using namespace std; // 主函数,程序的入口 int main() {// 局部变量声明// 程序逻辑代码// 返回值,表示程序正常结束…...

Java动态代理详解
文章目录 一、JDK动态代理1、关键类和接口2、实现步骤 二、CGLIB动态代理1、关键类2、实现步骤 三、总结 Java中的动态代理是一种设计模式,它允许在运行时创建代理对象,而不是在编译时。代理对象可以用来代理真实对象的方法调用。 Java中的动态代理主要…...

Python基础学习文档
一、Python入门 1.Python简介: Python是一种高级编程语言,用于多种应用,包括网站开发、数据科学、人工智能等。 Python具有语法简洁、易读性强、功能强大等特点。 2.安装Python ①访问Python官网(https://www.python.org/&am…...

数据结构与算法笔记:基础篇 - 分治算法:谈一谈大规模计算框架MapReduce中的分治思想
概述 MapReduce 是 Google 大数据处理的三姐马车之一,另外两个事 GFS 和 Bigtable。它在倒排索引、PageRank 计算、网页分析等搜索引擎相关的技术中都有大量的应用。 尽管开发一个 MapReduce 看起来很高深。实际上,万变不离其宗,它的本质就…...

如何清除anaconda3缓存?
如果长期使用anaconda不清理缓存,会导致anaconda占用磁盘空间越来越多,甚至系统磁盘撑爆。 清除包缓存: 打开 Anaconda Prompt 或者命令行窗口。运行以下命令清除包缓存:conda clean --all这会清除所有的包缓存,释放磁…...

智慧校园发展趋势:2024年及未来教育科技展望
展望2024年及未来的教育科技领域,智慧校园的发展正引领着一场教育模式的深刻变革,其核心在于更深层次地融合技术与教育实践。随着人工智能技术的不断成熟,个性化学习将不再停留于表面,而是深入到每个学生的个性化需求之中。通过精…...
【Python机器学习系列】针对特定数据构建管道流水线进行机器学习预测(案例+源码)
这是我的第305篇原创文章。 一、引言 机器学习项目中有可以自动化的标准工作流程。在 Python scikit-learn 中,管道有助于明确定义和自动化这些工作流程。使用pipeline后,我们每一步的输出都会自动的作为下一个的输入。一套完整的机器学习应用流程如下&a…...

Python 学习 第三册 第12章 图的最优化问题
----用教授的方式学习。 目录 12.1图的最优化问题 12.1.1最短路径:深度优先搜索和广度优先搜索 12.1图的最优化问题 我们下面研究另一种最优化问题。假设你有一个航空公司航线的价格列表,其中包括美国任意两个城市之间的航班价格。假设有3个城市A、B和C,从A出发经过B到达…...

建筑工程乙级资质与工程质量控制体系的构建
1. 质量管理体系建立 ISO 9001认证:虽然不是直接要求,但许多乙级资质企业会选择通过ISO 9001质量管理体系认证,以标准化管理流程,提升质量管理水平。质量方针与目标:明确企业的质量方针,设定可量化、可追踪…...

kafka学习笔记07
Kafka高可用集群搭建节点需求规划 开放端口。 Kafka高可用集群之zookeeper集群搭建环境准备 删除之前的kafka和zookeeper。 重新进行环境部署: 我们解压我们的zookeeper: 编辑第一个zookeeper的配置文件: 我们重复类似的操作,创建三个zookeeper节点: 记…...
MQTTfx连接阿里云(详细版)
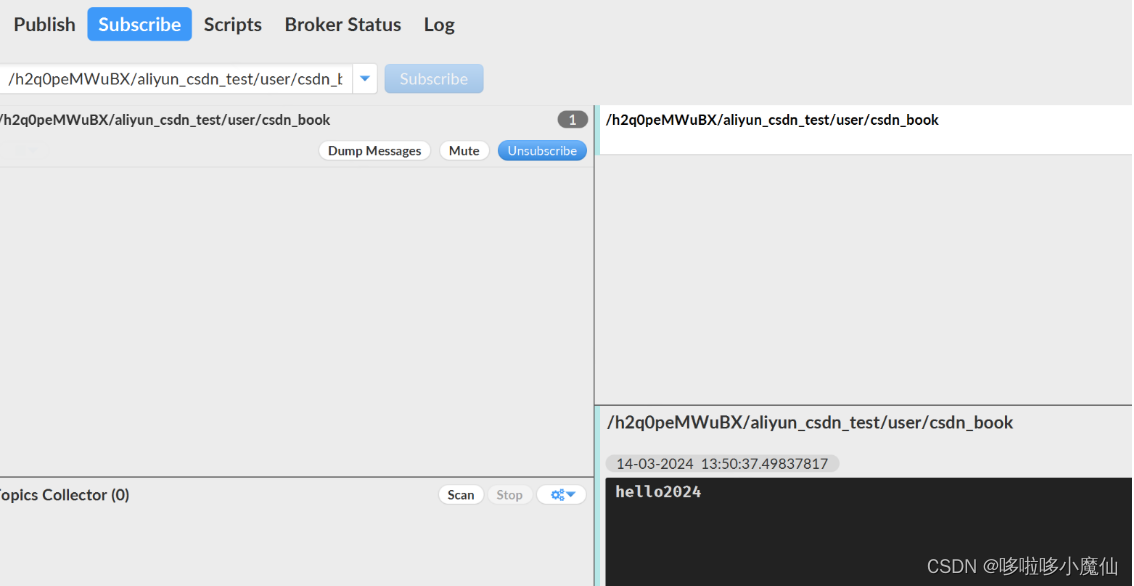
1、介绍 作为物联网开放平台,阿里云可谓是吸引大多数嵌入式爱好者的平台。物联网MQTT协议火热的今天,你使用过阿里云吗?本篇文章带你接触阿里云,实现MQTT通信。 我们在测试MQTT之前先了解下什么是MQTT协议。大家都知道它是一种发…...

Vue3使用provide和inject实现孙组件给爷组件传递数据
前言: 最近在研究gitHub中的一个项目并将与自己之前完成的项目进行结合,其中有一个功能是需要在孙组件将数据传递给爷组件,笔者研究后将使用总结如下: 具体步骤: 1.爷组件先定义一个空的函数传递给孙子 2.孙组件使…...
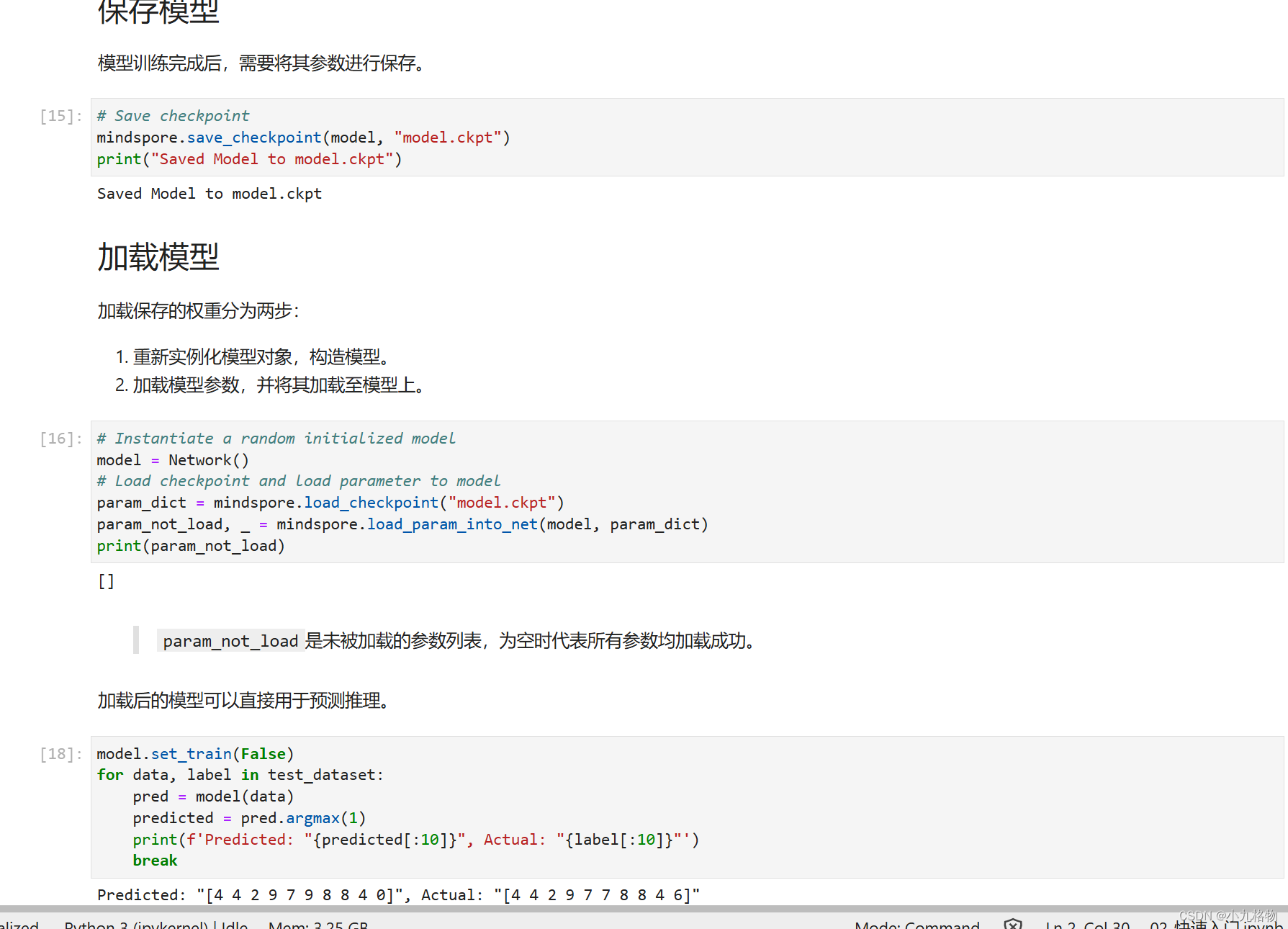
昇思25天学习打卡营第1天|基本介绍及快速入门
1.第一天学习总体复盘 1)成功注册昇思大模型平台,并成功申请算力; 2)在jupyter环境下学习初学入门/初学教程的内容; 在基本介绍部分,快速撸了一边内容,有了一个基本的了解(没理解到位的计划采用…...

C#.Net筑基-类型系统②常见类型
01、结构体类型Struct 结构体 struct 是一种用户自定义的值类型,常用于定义一些简单(轻量)的数据结构。对于一些局部使用的数据结构,优先使用结构体,效率要高很多。 可以有构造函数,也可以没有。因此初始…...

使用docker在3台服务器上搭建基于redis 6.x的一主两从三台均是哨兵模式
一、环境及版本说明 如果服务器已经安装了docker,则忽略此步骤,如果没有安装,则可以按照一下方式安装: 1. 在线安装(有互联网环境): 请看我这篇文章 传送阵>> 点我查看 2. 离线安装(内网环境):请看我这篇文章 传送阵>> 点我查看 说明:假设每台服务器已…...

Java 8 Stream API 入门到实践详解
一、告别 for 循环! 传统痛点: Java 8 之前,集合操作离不开冗长的 for 循环和匿名类。例如,过滤列表中的偶数: List<Integer> list Arrays.asList(1, 2, 3, 4, 5); List<Integer> evens new ArrayList…...

【HTML-16】深入理解HTML中的块元素与行内元素
HTML元素根据其显示特性可以分为两大类:块元素(Block-level Elements)和行内元素(Inline Elements)。理解这两者的区别对于构建良好的网页布局至关重要。本文将全面解析这两种元素的特性、区别以及实际应用场景。 1. 块元素(Block-level Elements) 1.1 基本特性 …...

用docker来安装部署freeswitch记录
今天刚才测试一个callcenter的项目,所以尝试安装freeswitch 1、使用轩辕镜像 - 中国开发者首选的专业 Docker 镜像加速服务平台 编辑下面/etc/docker/daemon.json文件为 {"registry-mirrors": ["https://docker.xuanyuan.me"] }同时可以进入轩…...

QT: `long long` 类型转换为 `QString` 2025.6.5
在 Qt 中,将 long long 类型转换为 QString 可以通过以下两种常用方法实现: 方法 1:使用 QString::number() 直接调用 QString 的静态方法 number(),将数值转换为字符串: long long value 1234567890123456789LL; …...

有限自动机到正规文法转换器v1.0
1 项目简介 这是一个功能强大的有限自动机(Finite Automaton, FA)到正规文法(Regular Grammar)转换器,它配备了一个直观且完整的图形用户界面,使用户能够轻松地进行操作和观察。该程序基于编译原理中的经典…...

html css js网页制作成品——HTML+CSS榴莲商城网页设计(4页)附源码
目录 一、👨🎓网站题目 二、✍️网站描述 三、📚网站介绍 四、🌐网站效果 五、🪓 代码实现 🧱HTML 六、🥇 如何让学习不再盲目 七、🎁更多干货 一、👨…...

动态 Web 开发技术入门篇
一、HTTP 协议核心 1.1 HTTP 基础 协议全称 :HyperText Transfer Protocol(超文本传输协议) 默认端口 :HTTP 使用 80 端口,HTTPS 使用 443 端口。 请求方法 : GET :用于获取资源,…...

MFC 抛体运动模拟:常见问题解决与界面美化
在 MFC 中开发抛体运动模拟程序时,我们常遇到 轨迹残留、无效刷新、视觉单调、物理逻辑瑕疵 等问题。本文将针对这些痛点,详细解析原因并提供解决方案,同时兼顾界面美化,让模拟效果更专业、更高效。 问题一:历史轨迹与小球残影残留 现象 小球运动后,历史位置的 “残影”…...

CRMEB 中 PHP 短信扩展开发:涵盖一号通、阿里云、腾讯云、创蓝
目前已有一号通短信、阿里云短信、腾讯云短信扩展 扩展入口文件 文件目录 crmeb\services\sms\Sms.php 默认驱动类型为:一号通 namespace crmeb\services\sms;use crmeb\basic\BaseManager; use crmeb\services\AccessTokenServeService; use crmeb\services\sms\…...

