【C++题解】1670 - 象棋大赛
问题:1670 - 象棋大赛
类型:分支问题
题目描述:
市里要组织象棋大赛,年龄在 8∼30 周岁之间的选手可以报名参赛。为了公平起见,大赛组委会将选手们分了青年组、少年组和儿童组,大赛组委会规定:
15∼30 周岁之间的选手为青年组选手、11∼14 周岁之间的选手为少年组选手、8∼10 周岁的选手为儿童组选手。
请从键盘读入一名选手的年龄,输出他应该分到哪一组。
青年组请输出 qingnianzu 、少年组请输出 shaonianzu 、儿童组请输出 ertongzu 。
输入:
输入一个整数 n 代表某位选手的年龄(n 是8∼30 之间的整数)。
输出:
输出该选手的分组。
样例:
输入:
28
输出:
qingnianzu
完整代码如下:
#include<bits/stdc++.h>
using namespace std;
int main(){//一、分析问题//已知:某位选手的年龄;//未知:他应该分到哪一组?青年组请输出 qingnianzu 、少年组请输出 shaonianzu 、儿童组请输出 ertongzu 。//关系:15~30 周岁之间的选手为青年组选手、11~14 周岁之间的选手为少年组选手、8~10 周岁的选手为儿童组选手。//二、数据定义 int n;//三、数据输入 cin>>n;//四、数据计算 if(n>=8&&n<=10){//五、输出结果 cout<<"ertongzu";}else if(n>=11&&n<=14){//五、输出结果 cout<<"shaonianzu";}else{//五、输出结果 cout<<"qingnianzu";}return 0;
}
相关文章:

【C++题解】1670 - 象棋大赛
问题:1670 - 象棋大赛 类型:分支问题 题目描述: 市里要组织象棋大赛,年龄在 8∼30 周岁之间的选手可以报名参赛。为了公平起见,大赛组委会将选手们分了青年组、少年组和儿童组,大赛组委会规定:…...

Samba:用于高效无限上下文语言建模的简单混合状态空间模型
Samba: Simple Hybrid State Space Models for Efficient Unlimited Context Language Modeling 📜 文献卡 Samba: Simple Hybrid State Space Models for Efficient Unlimited Context Language Modeling作者: Liliang Ren; Yang Liu; Yadong Lu; Yelong Shen; …...

通俗易懂的ChatGPT原理简介
一、引言 随着人工智能的发展,聊天机器人已经成为我们生活中的常见工具。而在众多聊天机器人中,ChatGPT 无疑是最受关注的一个。ChatGPT 是由 OpenAI 开发的一种基于生成式预训练模型(GPT)的大型语言模型。本文将通俗易懂地介绍 …...
你认为 AI 作图程序「MidJourney」有哪些比较好用的关键词?
玩了一段时间的MidJourney,打算把这个回答做成资源帖。也欢迎在评论区补充讨论。 MidJourney的极简指南 快速上手 装discord,或者直接打开网址 https://discord.gg/midjourney 注册用户。进入Midjourney的官方服务器后,在左侧栏找一个newb…...
excute()方法)
9.2JavaEE——JDBCTemplate的常用方法(一)excute()方法
execute()方法用于执行SQL语句,其语法格式如下: jdTemplate.execute("SQL 语句");下面以创建数据表的SQL语句为例,来演示excute()方法的使用,具体步骤如下。 1、创建数据库 在MySQL中,创建一个名为spring的…...

正向代理和反向代理的区别
正向代理和反向代理的主要区别在于代理服务器所服务的对象不同。 正向代理(Forward Proxy):正向代理的客户端是内部网络的用户。当内部网络的用户想要访问外部网络(例如互联网)时,可以通过正向代理服务器来…...
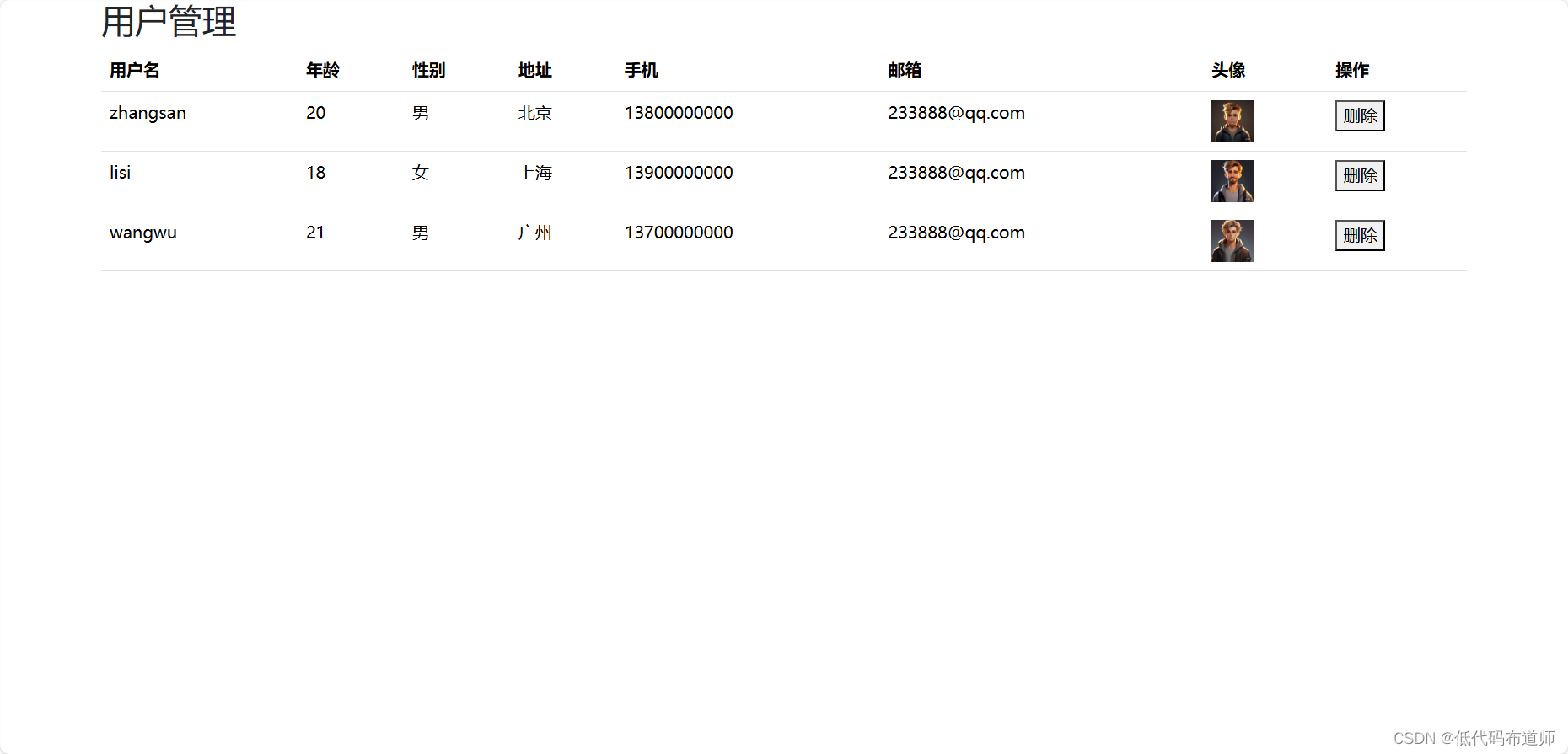
express入门03增删改查
目录 1 搭建服务器2 静态文件托管3 引入bootstrap4 引入jquery5 编写后端接口5.1 添加列表查询方法5.2 添加路由5.3 添加数据表格 总结 我们前两篇介绍了如何利用express搭建服务器,如何实现静态资源托管。那利用这两篇的知识点,我们就可以实现一个小功能…...
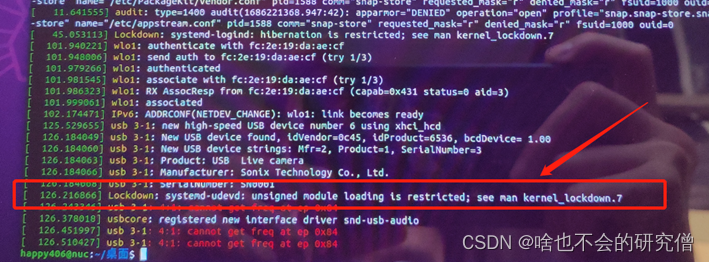
【usb设备端口异常】——使用ls /dev/video*查看设备号时出现报错:ls:无法访问‘/dev/video*‘: 没有那个文件或目录
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 前言一、ls:无法访问/dev/video*: 没有那个文件或目录1. 问题描述2. 原因分析3. 解决方法 总结 前言 一、ls:无法访问’/dev/video*: 没有那个文件或目录 使用的这…...

Java实现异步开发的方式
1)、继承 Thread 2)、实现 Runnable 接口 3)、实现 Callable 接口 FutureTask (可以拿到返回结果,可以处理异常) 4)、使用线程池 区别:1、2)不能得到返回值 …...

小知识点快速总结:Batch Normalization Layer(BN层)的作用
本系列文章只做简要总结,不详细说明原理和公式。 目录 1. 参考文章2. 主要作用3. 具体分析3.1 正则化,降低过拟合3.2 提高模型收敛速度,加速训练3.3 减少梯度爆炸或者梯度消失的情况 4. 补充4.1 BN层做的是标准化不是归一化4.2 BN层的公式4.…...
【SpringCloud】负载均衡(Spring Cloud LoadBalancer)
负载均衡 当服务流量增大时,通常会采用增加机器的方式进行扩容。负载均衡就是用来在多个机器或者其他资源中,按照一定的规则合理分配负载。其中的实现可以分成客户端负载均衡和服务端负载均衡。 服务端负载均衡 在服务端进行负载均衡的算法分配。 比…...

三生随记——输入法之谜
在深夜的电脑前,李浩专心致志地敲打着键盘,为他的小说写下最后一章。然而,随着他不断输入文字,他渐渐察觉到一丝不对劲。每次他尝试输入特定的词汇,输入法都会自动跳转到一些与主题毫不相关的句子,甚至有些…...

【名词解释】Unity中的3D物理系统:刚体
Unity中的3D物理系统是用于模拟现实世界中物体的运动和相互作用的一套工具和组件。刚体(Rigidbody)是Unity 3D物理系统中的一个核心组件,它允许游戏对象(GameObject)受到重力和外力的影响,并参与碰撞检测。…...
icon转svg处理
一般情况下,图标我们可以找UI或者去iconfont.cn获得一个svg格式的文件。然后再IDE中以文本的方式打开,然后格式化,就可以看到代码。代码中一般是最外层一个svg标签,里面是一个或者多个path。这个时候,我们使用h方法来实…...

已成功见刊检索的国际学术会议论文海报展示(2)
【先投稿先送审】第四届计算机、物联网与控制工程国际学术会议(CITCE 2024) 大会官网:www.citce.org 时间地点:2024年11月1-3日,中国-武汉 收录检索:EI Compendex,Scopus 主办单位:四川师范…...

EasyCVR/EasyDSS无人机直播技术助力野生动物监测
近日有新闻报道,一名挖掘机师傅在清理河道时,意外挖出一只稀有的扬子鳄,挖机师傅小心翼翼地将其放在一边,扬子鳄也顺势游回一旁的河道中。 随着人类对自然环境的不断探索和开发,野生动物及其栖息地的保护显得愈发重要。…...

AI视频教程下载-ChatGPT 生产力 + 时间管理
ChatGPT Productivity Time Management. ChatGPT Productivity ChatGPT 显著提升生产力 不寻常的时间管理技巧。ChatGPT 工作,Chat GPT 自动化,ChatGPT 2023! 对关于ChatGPT的讨论感到好奇,想知道如何利用它为自己带来好处吗&a…...

Java 集合框架:LinkedList 的介绍、使用、原理与源码解析
大家好,我是栗筝i,这篇文章是我的 “栗筝i 的 Java 技术栈” 专栏的第 014 篇文章,在 “栗筝i 的 Java 技术栈” 这个专栏中我会持续为大家更新 Java 技术相关全套技术栈内容。专栏的主要目标是已经有一定 Java 开发经验,并希望进…...

【Ruby爬虫01】某吃瓜网站图片数据采集
介绍 由于最近在学习Ruby,写一个爬虫锻炼一下。涉及xml解析、多线程、xpath语法等基础知识。 实现代码 使用说明 使用前请先安装如下gem gem install nokogiri http openssl# nokogiri:一个解析xml和html的库,支持css、xpath语法 # htt…...

可以免费领取tokens的大模型服务
本文更新时间:2024年6月20日 豆包大模型 “亲爱的客户,模型提供方将在5月15日至8月30日期间,为您提供一次独特的机会,即高达5亿tokens的免费权益。这是我们对您长期支持的感谢,也是对未来合作的期待。” 在8月30日之…...

wordpress后台更新后 前端没变化的解决方法
使用siteground主机的wordpress网站,会出现更新了网站内容和修改了php模板文件、js文件、css文件、图片文件后,网站没有变化的情况。 不熟悉siteground主机的新手,遇到这个问题,就很抓狂,明明是哪都没操作错误&#x…...

Chapter03-Authentication vulnerabilities
文章目录 1. 身份验证简介1.1 What is authentication1.2 difference between authentication and authorization1.3 身份验证机制失效的原因1.4 身份验证机制失效的影响 2. 基于登录功能的漏洞2.1 密码爆破2.2 用户名枚举2.3 有缺陷的暴力破解防护2.3.1 如果用户登录尝试失败次…...

【人工智能】神经网络的优化器optimizer(二):Adagrad自适应学习率优化器
一.自适应梯度算法Adagrad概述 Adagrad(Adaptive Gradient Algorithm)是一种自适应学习率的优化算法,由Duchi等人在2011年提出。其核心思想是针对不同参数自动调整学习率,适合处理稀疏数据和不同参数梯度差异较大的场景。Adagrad通…...

什么?连接服务器也能可视化显示界面?:基于X11 Forwarding + CentOS + MobaXterm实战指南
文章目录 什么是X11?环境准备实战步骤1️⃣ 服务器端配置(CentOS)2️⃣ 客户端配置(MobaXterm)3️⃣ 验证X11 Forwarding4️⃣ 运行自定义GUI程序(Python示例)5️⃣ 成功效果
HashMap中的put方法执行流程(流程图)
1 put操作整体流程 HashMap 的 put 操作是其最核心的功能之一。在 JDK 1.8 及以后版本中,其主要逻辑封装在 putVal 这个内部方法中。整个过程大致如下: 初始判断与哈希计算: 首先,putVal 方法会检查当前的 table(也就…...

WebRTC从入门到实践 - 零基础教程
WebRTC从入门到实践 - 零基础教程 目录 WebRTC简介 基础概念 工作原理 开发环境搭建 基础实践 三个实战案例 常见问题解答 1. WebRTC简介 1.1 什么是WebRTC? WebRTC(Web Real-Time Communication)是一个支持网页浏览器进行实时语音…...

多元隐函数 偏导公式
我们来推导隐函数 z z ( x , y ) z z(x, y) zz(x,y) 的偏导公式,给定一个隐函数关系: F ( x , y , z ( x , y ) ) 0 F(x, y, z(x, y)) 0 F(x,y,z(x,y))0 🧠 目标: 求 ∂ z ∂ x \frac{\partial z}{\partial x} ∂x∂z、 …...
)
背包问题双雄:01 背包与完全背包详解(Java 实现)
一、背包问题概述 背包问题是动态规划领域的经典问题,其核心在于如何在有限容量的背包中选择物品,使得总价值最大化。根据物品选择规则的不同,主要分为两类: 01 背包:每件物品最多选 1 次(选或不选&#…...
)
【系统架构设计师-2025上半年真题】综合知识-参考答案及部分详解(回忆版)
更多内容请见: 备考系统架构设计师-专栏介绍和目录 文章目录 【第1题】【第2题】【第3题】【第4题】【第5题】【第6题】【第7题】【第8题】【第9题】【第10题】【第11题】【第12题】【第13题】【第14题】【第15题】【第16题】【第17题】【第18题】【第19题】【第20~21题】【第…...

鸿蒙APP测试实战:从HDC命令到专项测试
普通APP的测试与鸿蒙APP的测试有一些共同的特征,但是也有一些区别,其中共同特征是,它们都可以通过cmd的命令提示符工具来进行app的性能测试。 其中区别主要是,对于稳定性测试的命令的区别,性能指标获取方式的命令的区…...
