掌握高等数学、线性代数、概率论所需数学知识及标题建议
在数学的广袤领域中,高等数学、线性代数和概率论作为三大核心分支,不仅在理论研究中占据重要地位,更在实际应用中发挥着举足轻重的作用。为了深入理解和掌握这三门学科,我们需要掌握一系列扎实的数学知识。
高等数学所需数学知识
高等数学是大学数学的重要组成部分,它以微积分为主要内容,研究函数、极限、导数、微分、积分等概念和方法。要学好高等数学,需要掌握以下数学知识:
- 基本代数知识:包括多项式的加减乘除、整式、有理式的化简和分解、方程和不等式的解法等。这些基础知识是高等数学中函数、极限等概念学习的基础。
- 初等函数知识:包括指数函数、对数函数、三角函数、反三角函数等的概念、性质和图像等。这些函数在高等数学中频繁出现,是理解和应用微积分的重要工具。
- 微积分基础知识:包括导数、微分、积分、微积分基本定理等。这些内容是高等数学的核心,也是后续学习的基础。
线性代数所需数学知识
线性代数是研究向量空间、线性变换及其性质的一门数学学科。在学习线性代数时,需要掌握以下数学知识:
- 基本代数知识:包括变量、方程、不等式、函数等基本概念和运算规则。这些基础知识是线性代数学习的基础。
- 矩阵和向量:了解矩阵的定义、性质和运算规则,以及向量的表示和运算方法。矩阵和向量是线性代数的基本研究对象。
- 行列式:掌握行列式的定义、性质和计算方法,包括展开定理和拉普拉斯定理等。行列式在解线性方程组、判断矩阵的逆等方面有重要应用。
- 线性方程组:理解线性方程组的概念和解法,包括高斯消元法和矩阵逆等方法。线性方程组是线性代数的重要研究对象之一。
此外,还需要了解矩阵的特征值和特征向量、线性空间和线性变换、向量空间的基和维数、线性映射和线性变换的核与像、内积空间和正交性、二次型和正定矩阵等概念和方法。
概率论所需数学知识
概率论是研究随机现象的数量规律的数学分支。在学习概率论时,需要掌握以下数学知识:
- 随机事件和概率:了解基本概念、性质和公式,以及重要概型如古典概型、几何概型、贝努利概型等。
- 随机变量及其分布:掌握一维随机变量和二维随机变量的分布,以及随机变量函数的分布。
- 重要的一维和二维分布:了解一维分布如(0-1)分布、二项分布、泊松分布、正态分布等,以及二维分布如二维均匀分布、二维正态分布等。
- 随机变量的数字特征:包括数学期望(平均值)、方差和标准差等。这些数字特征是描述随机变量特性的重要工具。
- 大数定律和中心极限定理:了解切比雪夫不等式、中心极限定理等重要公式与结论。
- 数理统计的基本概念:包括基本概念、性质与公式,以及三个抽样分布如x^2分布(卡方分布)、t分布与F分布等。
相关文章:
掌握高等数学、线性代数、概率论所需数学知识及标题建议
在数学的广袤领域中,高等数学、线性代数和概率论作为三大核心分支,不仅在理论研究中占据重要地位,更在实际应用中发挥着举足轻重的作用。为了深入理解和掌握这三门学科,我们需要掌握一系列扎实的数学知识。 高等数学所需数学知识 …...

value_and_grad
value_and_grad 是 JAX 提供的一个便捷函数,它同时计算函数的值和其梯度。这在优化过程中非常有用,因为在一次函数调用中可以同时获得损失值和相应的梯度。 以下是对 value_and_grad(loss, argnums0, has_auxFalse)(params, data, u, tol) 的详细解释&a…...

AI 已经在污染互联网了。。赛博喂屎成为现实
大家好,我是程序员鱼皮。这两年 AI 发展势头迅猛,更好的性能、更低的成本、更优的效果,让 AI 这一曾经高高在上的技术也走入大众的视野,能够被我们大多数普通人轻松使用,无需理解复杂的技术和原理。 其中,…...
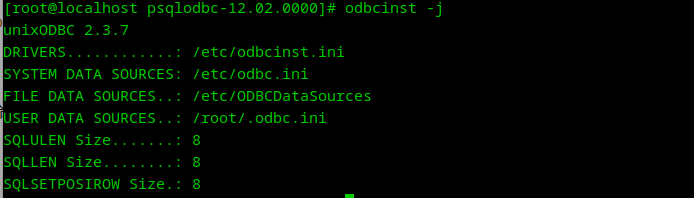
Linux系统安装ODBC驱动,统信服务器E版安装psqlodbc方法
应用场景 硬件/整机信息:AMD平台 OS版本信息:服务器e版 软件信息:psqlodbc 12.02版本 功能介绍 部分用户在使用etl工具连接数据库时,需要使用到odbc驱动,下面介绍下服务器e版系统中编译安装此工具的相关过程。 E…...

品牌对电商平台价格的监测流程
在当今的电商时代,品牌商会重点关注众多电商平台,如淘宝、天猫、京东、拼多多、苏宁、小红书、抖音、快手等。之所以这些平台备受瞩目,很大程度上是因为其上的店铺数量众多,情况复杂。如今,无论是品牌的经销商还是非经…...
osgearth提示“simple.earth: file not handled”
在用vcpkg编译完osg和osgearth后,为了验证osgearth编译是否正确,进行测试,模型加载代码如下: root->addChild(osgDB::readNodeFile("simple.earth")); 此时以为是simple.earth路径的问题,遂改为以下代码…...
hbuilderx如何打包ios app,如何生成证书
hbuilderx可以打包ios app, 但是打包的时候,却需要两个证书文件,我们又如何生成这两个证书文件呢? 点击hbuilderx的官网链接,教程是需要使用mac电脑苹果开发者账号去创建这两个文件,可是问题来了,我们没有…...

扩散模型荣获CVPR2024最佳论文奖,最新成果让评估和改进生成模型更加效率!
CVPR 2024最佳论文奖新鲜出炉 其中一篇是Rich Human Feedback for Text-to-Image Generation,受大模型中的RLHF技术启发,团队用人类反馈来改进Stable Diffusion等文生图模型。 作者提出了收集丰富的细粒度人类反馈信息,用于更好地评估和改进…...

通过CSS样式来禁用href
<style>.disabled-link {pointer-events: none;cursor: default;text-decoration: none;color: inherit; }</style><a href"https://www.example.com" class"disabled-link">禁用链接</a> 在上述CSS样式中, pointer-…...

汽车传动系统为汽车动力总成重要组成部分 我国市场参与者数量不断增长
汽车传动系统为汽车动力总成重要组成部分 我国市场参与者数量不断增长 汽车系统主要包括动力系统、制动系统、传动系统、转向系统、行驶系统、燃油供给系统、照明系统以及电器系统。汽车传动系统指能够将发动机产生的动力转化为车辆行驶驱动力的动力传递装置。汽车传动系统为汽…...
智慧校园软件解决方案:提升学校管理效率的最佳选择
在当今教育领域,智慧校园信息化方案正逐渐成为提升学校管理水平与教学品质的关键途径。这一方案融合了最新科技,通过数字化、网络化及智能化方式,全面革新教育资源分配与教育互动模式,旨在为学校带来以下核心价值与优势 1. 综合信…...

数据结构之B数
目录 1.概述 2.特点 3.诞生 4.优缺点 4.1.优点 4.2.缺点 5.应用场景 6.C语言中的B树实现例子 7.总结 1.概述 B树(B-tree)是一种自平衡的树数据结构,广泛应用于数据库和文件系统中,以便高效地进行顺序读取、写入以及查找…...

计算机基础必须知道的76个常识!沈阳计算机软件培训
01 信息技术是指人们获取、存储、传递、处理、开发和利用信息资源的相关技术。 02 1、计算机的特点: (1)运算速度快 (2)存储容量大 (3)通用性强 (4)工作自动化 &…...

7,KQM模块的驱动
1,查资料,查模块的通信接口(单片机和模块之间采用什么方式通信)硬件接口,驱动方式(串口驱动用串口发送接收PC10,PC11) 只用了三个脚:VCC GND T&…...

软件验收测试报告模版分享,如何获取专业的验收测试报告?
软件验收测试报告是对软件开发过程中的最后一步确认,通过对软件进行全面、系统的检查和测试,形成一份详细的报告,以评估软件是否满足用户需求和设计要求。验收测试报告起到了非常重要的作用,不仅可以帮助开发者了解软件开发的质量…...
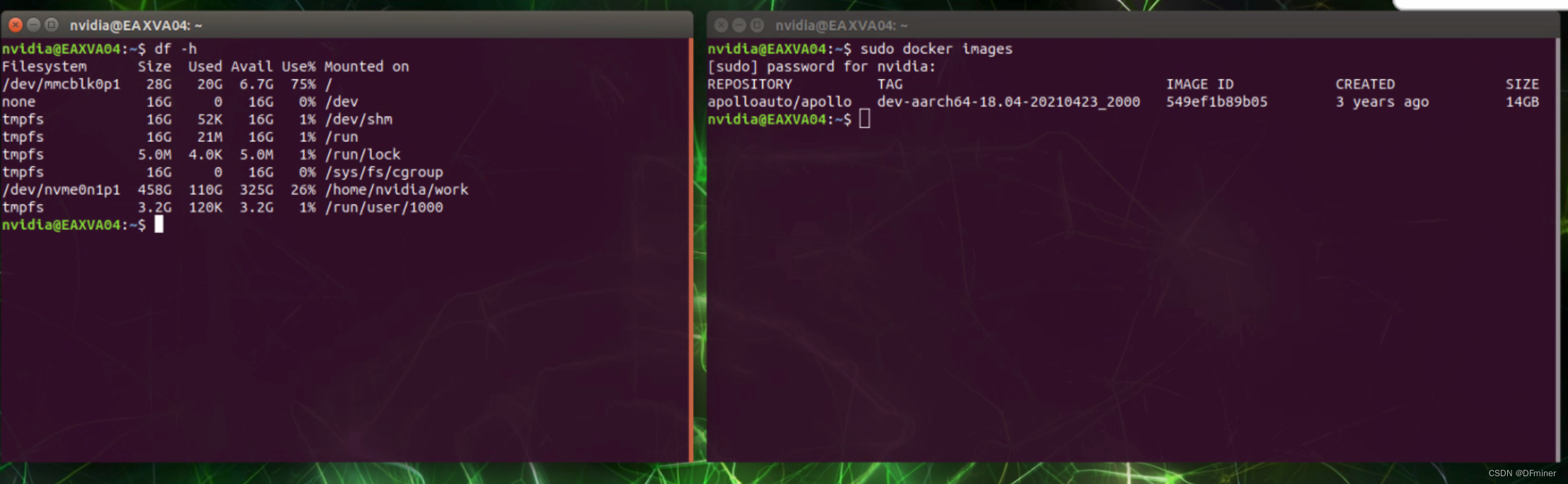
【arm扩容】docker load -i tar包 空间不足
背景: 首先我在/home/nvidia/work下导入了一些镜像源码tar包。然后逐个load进去。当我 load -i dev-aarch64-18.04-20210423_2000.tar包的时候,出现 Error processing tar file(exit status 1): write /9818cf5a7cbd5a828600d9a4d4e62185a7067e2a6f2ee…...

基于PID的直流电机自动控制系统的设计【MATLAB】
摘 要 本文在广泛查阅资料,了解直流电机特性的基础上,对直流电机的控制原理进行了的研究,设计了一款基于PID控制器的简单直流电机自动控制系统。 首先,分析了直流电机的应用背景和发展现状,对直流电机的工作原理和数学…...

MySQL----事务
MySQL 事务主要用于处理操作量大,复杂度高的数据。比如,在学校管理系统中,我们删除一个学生,既需要删除学生的基本资料,也要删除和该学生相关的信息,如班级,考试成绩等等,这样&#…...
客观评价,可道云teamOS搭建的企业网盘,如Windows本地电脑一般的使用体验真的蛮不错
不管是企业网盘还是私有网盘,简单易用一直是我比较在意的。快速能上手使用,甚至不需要习惯一套新的操作逻辑,代表着不需要学习适应,能够迅速投入正常使用。 在这个过程中,可道云teamos以其Windows电脑般的流畅体验&am…...

当页面中有多个echarts图表的时候,resize不生效的修改方法
一、本来的代码 var myChart1 this.$echarts.init(document.getElementById(‘xxxx’)); let option {}; myChart1.setOption(option); setTimeout(function () {window.onresize function () {myChart1.resize();} }, 200) 二、修改后的代码 var myChart1 this.$echart…...

练习(含atoi的模拟实现,自定义类型等练习)
一、结构体大小的计算及位段 (结构体大小计算及位段 详解请看:自定义类型:结构体进阶-CSDN博客) 1.在32位系统环境,编译选项为4字节对齐,那么sizeof(A)和sizeof(B)是多少? #pragma pack(4)st…...

云启出海,智联未来|阿里云网络「企业出海」系列客户沙龙上海站圆满落地
借阿里云中企出海大会的东风,以**「云启出海,智联未来|打造安全可靠的出海云网络引擎」为主题的阿里云企业出海客户沙龙云网络&安全专场于5.28日下午在上海顺利举办,现场吸引了来自携程、小红书、米哈游、哔哩哔哩、波克城市、…...

第一篇:Agent2Agent (A2A) 协议——协作式人工智能的黎明
AI 领域的快速发展正在催生一个新时代,智能代理(agents)不再是孤立的个体,而是能够像一个数字团队一样协作。然而,当前 AI 生态系统的碎片化阻碍了这一愿景的实现,导致了“AI 巴别塔问题”——不同代理之间…...

基于Docker Compose部署Java微服务项目
一. 创建根项目 根项目(父项目)主要用于依赖管理 一些需要注意的点: 打包方式需要为 pom<modules>里需要注册子模块不要引入maven的打包插件,否则打包时会出问题 <?xml version"1.0" encoding"UTF-8…...

【学习笔记】深入理解Java虚拟机学习笔记——第4章 虚拟机性能监控,故障处理工具
第2章 虚拟机性能监控,故障处理工具 4.1 概述 略 4.2 基础故障处理工具 4.2.1 jps:虚拟机进程状况工具 命令:jps [options] [hostid] 功能:本地虚拟机进程显示进程ID(与ps相同),可同时显示主类&#x…...
-HIve数据分析)
大数据学习(132)-HIve数据分析
🍋🍋大数据学习🍋🍋 🔥系列专栏: 👑哲学语录: 用力所能及,改变世界。 💖如果觉得博主的文章还不错的话,请点赞👍收藏⭐️留言Ǵ…...

Fabric V2.5 通用溯源系统——增加图片上传与下载功能
fabric-trace项目在发布一年后,部署量已突破1000次,为支持更多场景,现新增支持图片信息上链,本文对图片上传、下载功能代码进行梳理,包含智能合约、后端、前端部分。 一、智能合约修改 为了增加图片信息上链溯源,需要对底层数据结构进行修改,在此对智能合约中的农产品数…...

安宝特案例丨Vuzix AR智能眼镜集成专业软件,助力卢森堡医院药房转型,赢得辉瑞创新奖
在Vuzix M400 AR智能眼镜的助力下,卢森堡罗伯特舒曼医院(the Robert Schuman Hospitals, HRS)凭借在无菌制剂生产流程中引入增强现实技术(AR)创新项目,荣获了2024年6月7日由卢森堡医院药剂师协会࿰…...

HTML中各种标签的作用
一、HTML文件主要标签结构及说明 1. <!DOCTYPE html> 作用:声明文档类型,告知浏览器这是 HTML5 文档。 必须:是。 2. <html lang“zh”>. </html> 作用:包裹整个网页内容,lang"z…...
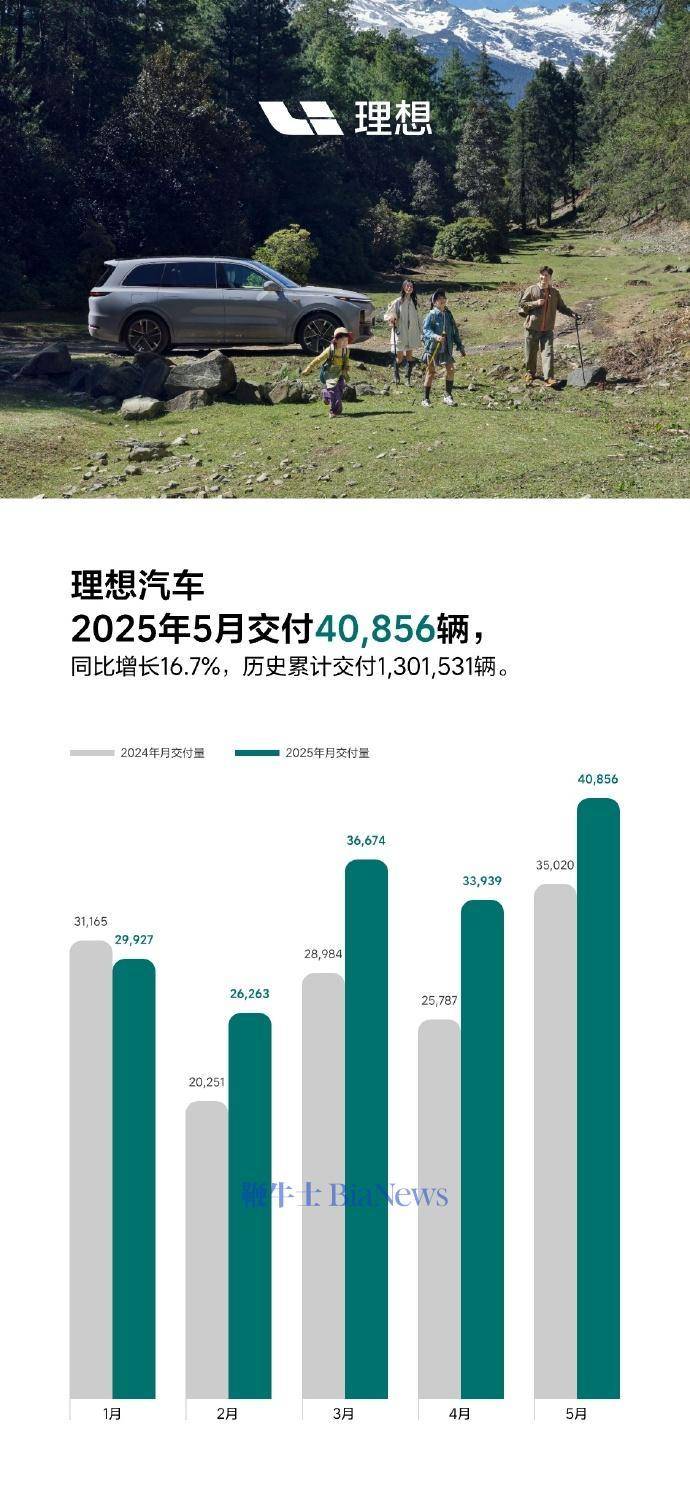
理想汽车5月交付40856辆,同比增长16.7%
6月1日,理想汽车官方宣布,5月交付新车40856辆,同比增长16.7%。截至2025年5月31日,理想汽车历史累计交付量为1301531辆。 官方表示,理想L系列智能焕新版在5月正式发布,全系产品力有显著的提升,每…...
