椭圆的矩阵表示法
椭圆的矩阵表示法
flyfish
1. 标准几何表示法
标准几何表示法是通过椭圆的几何定义来表示的:
x 2 a 2 + y 2 b 2 = 1 \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 a2x2+b2y2=1其中, a a a 是椭圆的长半轴长度, b b b 是椭圆的短半轴长度。

2. 线性代数表示法
线性代数表示法是通过椭圆的二次型表示的:
x T Σ − 1 x = c \mathbf{x}^T \Sigma^{-1} \mathbf{x} = c xTΣ−1x=c其中, x \mathbf{x} x 是点的向量表示 ( x y ) \begin{pmatrix} x \\ y \end{pmatrix} (xy), Σ \Sigma Σ 是一个正定矩阵(协方差矩阵的逆), c c c 是一个常数。
推导两者之间的关系
我们通过具体推导来看这两者之间的关系:
假设我们有一个标准形式的椭圆方程:
x 2 a 2 + y 2 b 2 = 1 \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 a2x2+b2y2=1
可以将其改写为矩阵形式:
( x y ) ( 1 a 2 0 0 1 b 2 ) ( x y ) = 1 \begin{pmatrix} x & y \end{pmatrix} \begin{pmatrix} \frac{1}{a^2} & 0 \\ 0 & \frac{1}{b^2} \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix} = 1 (xy)(a2100b21)(xy)=1在这里,矩阵 ( 1 a 2 0 0 1 b 2 ) \begin{pmatrix} \frac{1}{a^2} & 0 \\ 0 & \frac{1}{b^2} \end{pmatrix} (a2100b21) 就是 Σ − 1 \Sigma^{-1} Σ−1,而常数 c = 1 c = 1 c=1。
因此,标准形式的椭圆方程可以被视为线性代数表示法的一种特例,其中:
Σ − 1 = ( 1 a 2 0 0 1 b 2 ) \Sigma^{-1} = \begin{pmatrix} \frac{1}{a^2} & 0 \\ 0 & \frac{1}{b^2} \end{pmatrix} Σ−1=(a2100b21)
这也意味着:
Σ = ( a 2 0 0 b 2 ) \Sigma = \begin{pmatrix} a^2 & 0 \\ 0 & b^2 \end{pmatrix} Σ=(a200b2)
更一般的情况
如果椭圆不是标准形式的(例如旋转过或者平移过的椭圆),其线性代数表示法中的矩阵 Σ \Sigma Σ 将不是对角矩阵,而是一个包含非零的非对角元素的矩阵。
1. 椭圆的几何定义
设椭圆的两个焦点分别为 F 1 ( − c , 0 ) F_1(-c, 0) F1(−c,0) 和 F 2 ( c , 0 ) F_2(c, 0) F2(c,0),椭圆上的任意一点 P ( x , y ) P(x, y) P(x,y) 满足以下条件:
P F 1 + P F 2 = 2 a PF_1 + PF_2 = 2a PF1+PF2=2a
其中, 2 a 2a 2a 是椭圆的长轴长度, a a a 是长半轴的长度。
2. 代入距离公式
根据距离公式,可以得到 P P P 到 F 1 F_1 F1 和 F 2 F_2 F2 的距离分别为:
P F 1 = ( x + c ) 2 + y 2 PF_1 = \sqrt{(x + c)^2 + y^2} PF1=(x+c)2+y2
P F 2 = ( x − c ) 2 + y 2 PF_2 = \sqrt{(x - c)^2 + y^2} PF2=(x−c)2+y2根据椭圆的定义,有:
( x + c ) 2 + y 2 + ( x − c ) 2 + y 2 = 2 a \sqrt{(x + c)^2 + y^2} + \sqrt{(x - c)^2 + y^2} = 2a (x+c)2+y2+(x−c)2+y2=2a
3. 消除根号
为了简化这个方程,我们首先将方程两边平方:
( ( x + c ) 2 + y 2 + ( x − c ) 2 + y 2 ) 2 = ( 2 a ) 2 \left( \sqrt{(x + c)^2 + y^2} + \sqrt{(x - c)^2 + y^2} \right)^2 = (2a)^2 ((x+c)2+y2+(x−c)2+y2)2=(2a)2展开左边:
( x + c ) 2 + y 2 + ( x − c ) 2 + y 2 + 2 ( ( x + c ) 2 + y 2 ) ( ( x − c ) 2 + y 2 ) = 4 a 2 (x + c)^2 + y^2 + (x - c)^2 + y^2 + 2 \sqrt{((x + c)^2 + y^2)((x - c)^2 + y^2)} = 4a^2 (x+c)2+y2+(x−c)2+y2+2((x+c)2+y2)((x−c)2+y2)=4a2
4. 凑平方差
我们先简化左边的前两项:
( x + c ) 2 + y 2 + ( x − c ) 2 + y 2 = x 2 + 2 x c + c 2 + y 2 + x 2 − 2 x c + c 2 + y 2 (x + c)^2 + y^2 + (x - c)^2 + y^2 = x^2 + 2xc + c^2 + y^2 + x^2 - 2xc + c^2 + y^2 (x+c)2+y2+(x−c)2+y2=x2+2xc+c2+y2+x2−2xc+c2+y2
= 2 x 2 + 2 y 2 + 2 c 2 = 2x^2 + 2y^2 + 2c^2 =2x2+2y2+2c2代入上面的方程得到:
2 x 2 + 2 y 2 + 2 c 2 + 2 ( ( x + c ) 2 + y 2 ) ( ( x − c ) 2 + y 2 ) = 4 a 2 2x^2 + 2y^2 + 2c^2 + 2 \sqrt{((x + c)^2 + y^2)((x - c)^2 + y^2)} = 4a^2 2x2+2y2+2c2+2((x+c)2+y2)((x−c)2+y2)=4a2移项得到:
2 ( ( x + c ) 2 + y 2 ) ( ( x − c ) 2 + y 2 ) = 4 a 2 − 2 x 2 − 2 y 2 − 2 c 2 2 \sqrt{((x + c)^2 + y^2)((x - c)^2 + y^2)} = 4a^2 - 2x^2 - 2y^2 - 2c^2 2((x+c)2+y2)((x−c)2+y2)=4a2−2x2−2y2−2c2
( ( x + c ) 2 + y 2 ) ( ( x − c ) 2 + y 2 ) = 2 a 2 − x 2 − y 2 − c 2 \sqrt{((x + c)^2 + y^2)((x - c)^2 + y^2)} = 2a^2 - x^2 - y^2 - c^2 ((x+c)2+y2)((x−c)2+y2)=2a2−x2−y2−c2
5. 消去根号
为了继续消去根号,我们再次平方两边:
( ( ( x + c ) 2 + y 2 ) ( ( x − c ) 2 + y 2 ) ) 2 = ( 2 a 2 − x 2 − y 2 − c 2 ) 2 \left( \sqrt{((x + c)^2 + y^2)((x - c)^2 + y^2)} \right)^2 = (2a^2 - x^2 - y^2 - c^2)^2 (((x+c)2+y2)((x−c)2+y2))2=(2a2−x2−y2−c2)2展开左边:
( ( x + c ) 2 + y 2 ) ( ( x − c ) 2 + y 2 ) = ( 2 a 2 − x 2 − y 2 − c 2 ) 2 ((x + c)^2 + y^2)((x - c)^2 + y^2) = (2a^2 - x^2 - y^2 - c^2)^2 ((x+c)2+y2)((x−c)2+y2)=(2a2−x2−y2−c2)2
6. 简化方程
左边的展开:
( x 2 + 2 x c + c 2 + y 2 ) ( x 2 − 2 x c + c 2 + y 2 ) (x^2 + 2xc + c^2 + y^2)(x^2 - 2xc + c^2 + y^2) (x2+2xc+c2+y2)(x2−2xc+c2+y2)
= ( x 2 + y 2 + c 2 ) 2 − ( 2 x c ) 2 = (x^2 + y^2 + c^2)^2 - (2xc)^2 =(x2+y2+c2)2−(2xc)2
= ( x 2 + y 2 + c 2 ) 2 − 4 x 2 c 2 = (x^2 + y^2 + c^2)^2 - 4x^2c^2 =(x2+y2+c2)2−4x2c2右边的展开:
( 2 a 2 − x 2 − y 2 − c 2 ) 2 (2a^2 - x^2 - y^2 - c^2)^2 (2a2−x2−y2−c2)2
= 4 a 4 − 4 a 2 ( x 2 + y 2 + c 2 ) + ( x 2 + y 2 + c 2 ) 2 = 4a^4 - 4a^2(x^2 + y^2 + c^2) + (x^2 + y^2 + c^2)^2 =4a4−4a2(x2+y2+c2)+(x2+y2+c2)2令左边和右边相等:
( x 2 + y 2 + c 2 ) 2 − 4 x 2 c 2 = 4 a 4 − 4 a 2 ( x 2 + y 2 + c 2 ) + ( x 2 + y 2 + c 2 ) 2 (x^2 + y^2 + c^2)^2 - 4x^2c^2 = 4a^4 - 4a^2(x^2 + y^2 + c^2) + (x^2 + y^2 + c^2)^2 (x2+y2+c2)2−4x2c2=4a4−4a2(x2+y2+c2)+(x2+y2+c2)2相消掉相同项后:
− 4 x 2 c 2 = 4 a 4 − 4 a 2 ( x 2 + y 2 + c 2 ) - 4x^2c^2 = 4a^4 - 4a^2(x^2 + y^2 + c^2) −4x2c2=4a4−4a2(x2+y2+c2)
x 2 c 2 = a 2 ( x 2 + y 2 + c 2 ) − a 4 x^2c^2 = a^2(x^2 + y^2 + c^2) - a^4 x2c2=a2(x2+y2+c2)−a4由于 c 2 = a 2 − b 2 c^2 = a^2 - b^2 c2=a2−b2,我们将其代入上式中:
x 2 ( a 2 − b 2 ) = a 2 ( x 2 + y 2 + ( a 2 − b 2 ) ) − a 4 x^2(a^2 - b^2) = a^2(x^2 + y^2 + (a^2 - b^2)) - a^4 x2(a2−b2)=a2(x2+y2+(a2−b2))−a4
x 2 a 2 − x 2 b 2 = a 2 x 2 + a 2 y 2 + a 4 − a 2 b 2 − a 4 x^2a^2 - x^2b^2 = a^2x^2 + a^2y^2 + a^4 - a^2b^2 - a^4 x2a2−x2b2=a2x2+a2y2+a4−a2b2−a4
x 2 a 2 − x 2 b 2 = a 2 x 2 + a 2 y 2 − a 2 b 2 x^2a^2 - x^2b^2 = a^2x^2 + a^2y^2 - a^2b^2 x2a2−x2b2=a2x2+a2y2−a2b2整理后得到:
− x 2 b 2 = a 2 y 2 − a 2 b 2 -x^2b^2 = a^2y^2 - a^2b^2 −x2b2=a2y2−a2b2
x 2 b 2 = a 2 b 2 − a 2 y 2 x^2b^2 = a^2b^2 - a^2y^2 x2b2=a2b2−a2y2
x 2 a 2 + y 2 b 2 = 1 \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 a2x2+b2y2=1
最终的标准椭圆方程
x 2 a 2 + y 2 b 2 = 1 \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 a2x2+b2y2=1
相关文章:

椭圆的矩阵表示法
椭圆的矩阵表示法 flyfish 1. 标准几何表示法 标准几何表示法是通过椭圆的几何定义来表示的: x 2 a 2 y 2 b 2 1 \frac{x^2}{a^2} \frac{y^2}{b^2} 1 a2x2b2y21其中, a a a 是椭圆的长半轴长度, b b b 是椭圆的短半轴长度。 2.…...
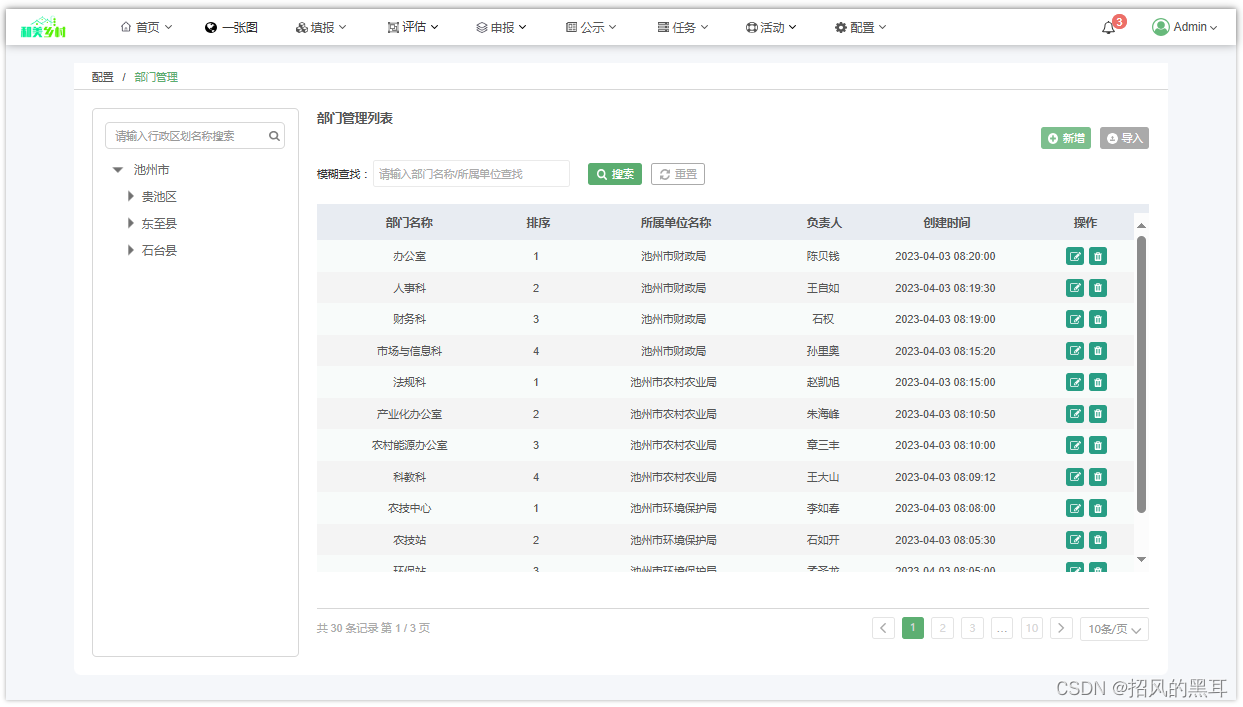
智慧乡村和美人家信息化系统
一、简介 智慧乡村和美人家信息化系统是一个综合管理平台,集成了首页概览、一张图可视化、数据填报、智能评估、便捷申报、公开公示、任务管理、活动发布和灵活配置等功能。该系统不仅提升了乡村管理效率,也优化了家庭生活的便捷性。通过一张图…...

ios-deploy - Required for installing your app on a physical device with the CLI
ios-deploy 是一个用于在 iOS 设备上安装、调试和运行 iOS 应用的开源工具。如果你正在使用命令行界面(CLI)来部署 React Native 或其他原生 iOS 应用到物理设备,那么安装 ios-deploy 是必要的。 以下是安装 ios-deploy 的一般步骤ÿ…...
thinkphp5使用模型删除与复杂查询EXP
模型删除 应用软删除 表中需要有字段,deletetime 模型中使用下面方法 use SoftDelete;protected $deleteTime delete_time;真实删除 // 软删除 User::destroy(1); // 真实删除 User::destroy(1,true); $user User::get(1); // 软删除 $user->delete(); // 真…...

铜陵市省重点实验室、省工程技术研究中心认定奖励补贴和申报认定条件流程归集
本文介绍铜陵市省重点实验室、省工程技术研究中心认定奖励补贴和申报认定条件等内容,详情如下,需要申报的可指导! 铜陵市省重点实验室、省工程技术研究中心认定奖励补贴(2023年发布) 对新认定的国家重点实验室、国家…...

Linux-目录和文件
目录 一、Linux目录 1、Linux常见目录 2、常见的Linux文件类型 二、cat-查看文件命令 1、cat命令用法 三、分页查看文件内容 1、 more命令 2、less命令 3、more和less的区别 四、查看文件开头或末尾 1、head命令 2、tail命令 3、wc-统计文件内容 4、grep 命令…...
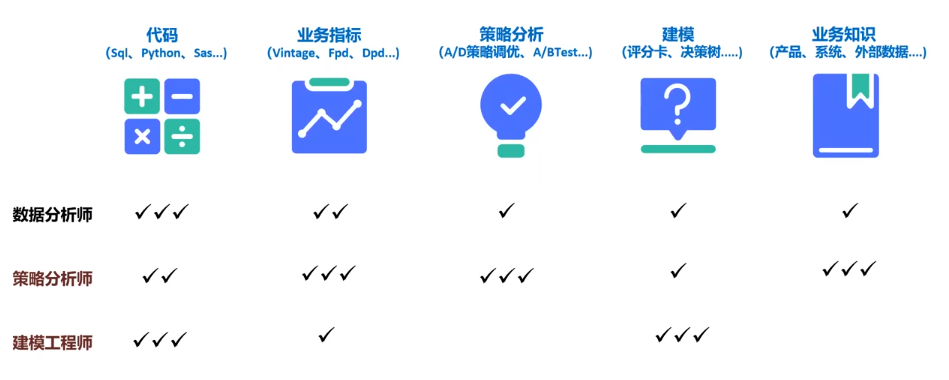
2024-06月 | 维信金科 | 风控数据岗位推荐,高收入岗位来袭!
今日推荐岗位:策略分析经理/分析专家、贷前、中策略分析、风控模型分析。 风控部门是金融业务的核心部门,而从事风控行业的人即称之为风险管理者。是大脑,是最最最重要的部门之一。今日推荐岗位的核心技能分布如下: 简历发送方式…...

不适合编程的人是怎样的?
你知道不适合编程的人是怎样的吗?其实,对编程没有兴趣的人往往都不适合从事编程工作。编程并非是一项轻松简单的任务,它需要投入大量的时间和精力。 编程领域有其独特的特点和要求。首先,编程有着相当陡峭的学习曲线。从最基础的语…...
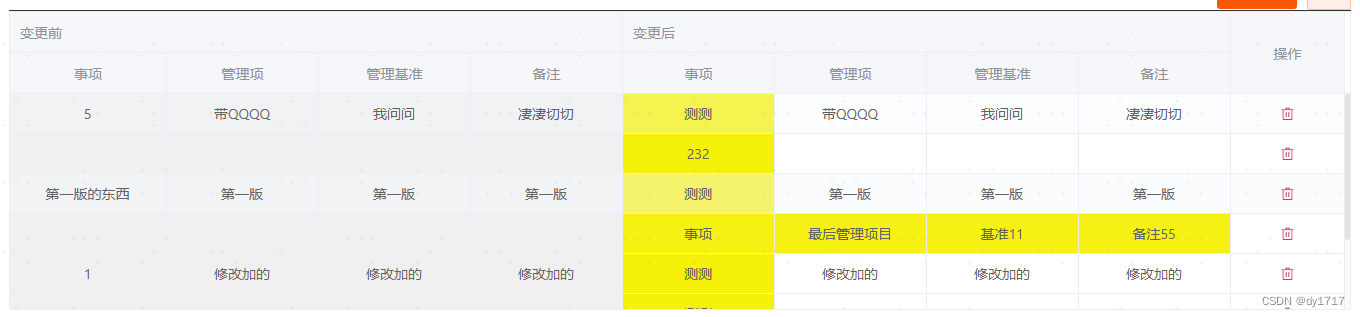
el-table表格变更前后根据数据值改变背景颜色
需求: 1.左侧变更前表格数据不可以编辑,并且背景色加灰 2.右侧变更后表格数据可被编辑,编辑后变更前与变更后行数据不一致,添加背景色区分 3.点击删除的时候,给变更后表格当前行,添加背景色和删除的中横…...

flask基础知识1
目录 1.介绍 2.体验一下 3.配置参数: 4.路由和URL 1.路由 2.动态路由: 自定义转换器: 3.使用自定义转换器 5.url_for函数 6.request参数 7.处理响应: 1.重定向: 2.返回json数据: 3.返回模板&…...

第8天:Django Admin高级配置
第8天:Django Admin高级配置 目标 定制Django Admin界面,提高数据管理效率。 任务概览 注册模型到Admin界面。定制Admin选项,如列表显示、搜索字段、过滤器等。 详细步骤 1. 注册模型到Admin界面 在Django Admin中注册模型,…...
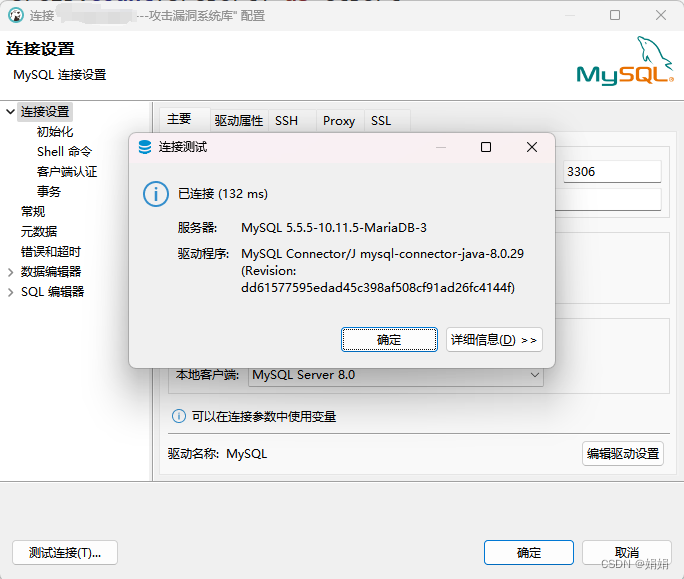
本地无法连接linux上的MariaDB数据库
问题:本地用DBeaver无法连接服务器上的MariaDB数据库 ? 测试1:在cmd中ping 服务器IP,看是否能ping通,能ping通,没有问题 测试2:在cmd中telnet 服务器IP 端口,看是否能访问…...

使用 Netty 自定义解码器处理粘包和拆包问题详解
使用 Netty 自定义解码器处理粘包和拆包问题详解 在网络编程中,粘包和拆包问题是常见的挑战。粘包是指多个数据包在传输过程中粘在一起,而拆包是指一个数据包在传输过程中被拆分成多个部分。Netty 是一个高性能、事件驱动的网络应用框架,提供…...

SDK编译IO Domain电压选择
开源鸿蒙硬件方案领跑者 触觉智能 本文适用于在Purple Pi OH开发板进行分区镜像烧录。触觉智能的Purple Pi OH鸿蒙开源主板,是华为Laval官方社区主荐的一款鸿蒙开发主板。 该主板主要针对学生党,极客,工程师,极大降低了开源鸿蒙…...
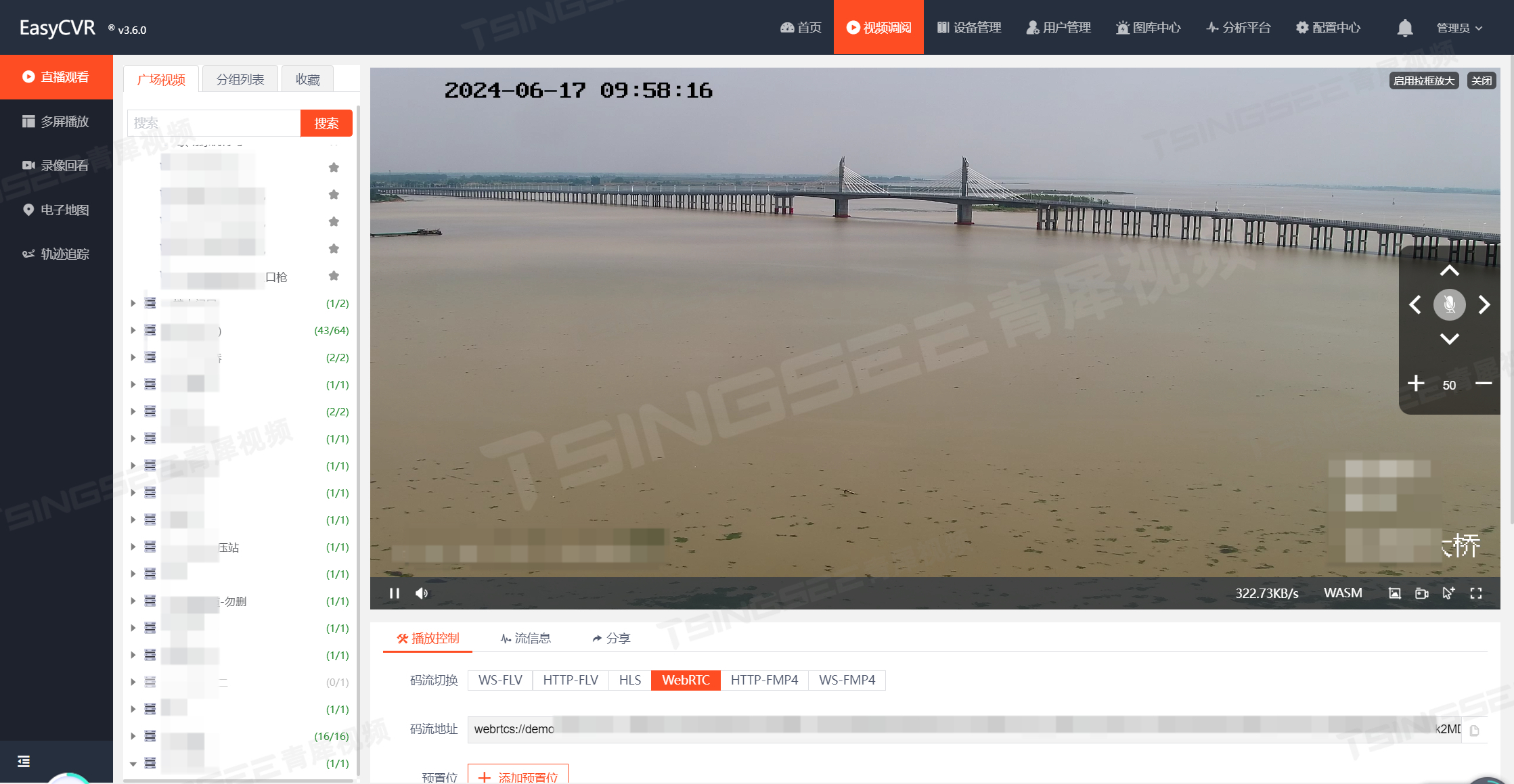
如何在纯内网环境下,将EasyCVR视频汇聚网关通过4G与第三方公网云平台级联?
EasyCVR视频汇聚网关是TSINGSEE青犀软硬一体的一款产品,可提供多协议的接入、音视频采集、处理,能实现海量前端设备的轻量化接入/转码/分发、视频直播、云端录像、云存储、检索回看、智能告警、平台级联等,兼容多种操作系统,轻松扩…...

2024-06-14 AI资讯:CCF论坛探讨大模型挑战,启动安全赛
智源社区 共话大模型技术进展与挑战,CCF大模型论坛北京会议圆满落幕! 2024 年 6 月 6 日中国计算机学会大模型论坛(CCF FoLM)主题会议在北京顺利举办。本次会议主题为“大模型技术进展与挑战”,各位专家围绕大模型技…...
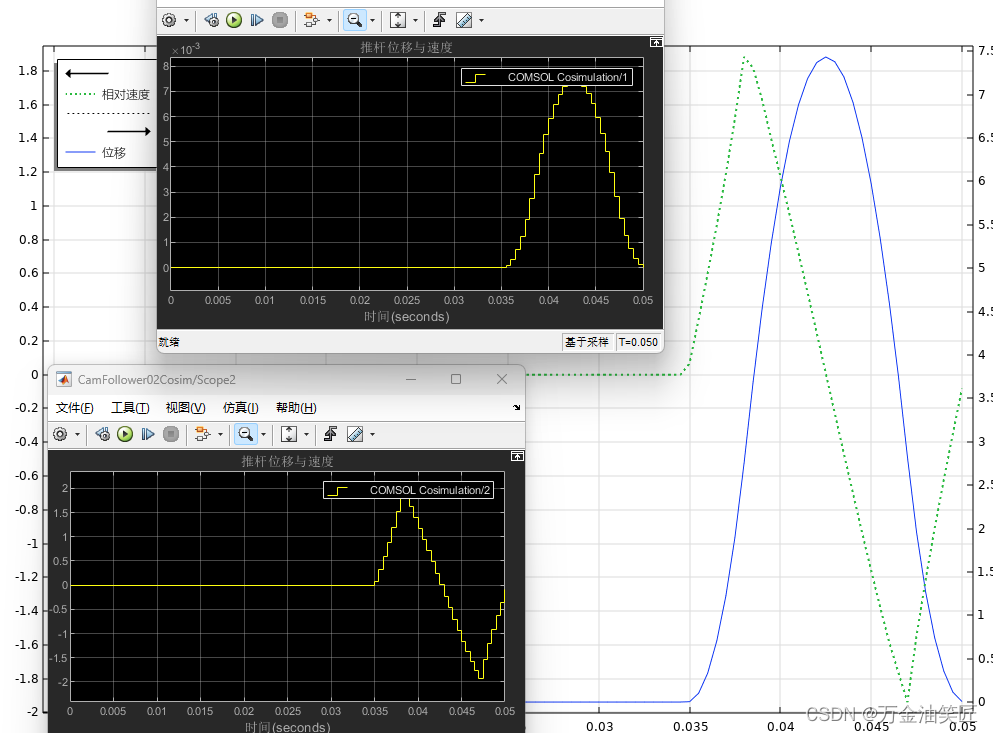
玩转Matlab-Simscape(初级)- 10 - 基于COMSOLSimulink 凸轮机构的控制仿真
** 玩转Matlab-Simscape(初级)- 10 - 基于COMSOL&Simulink 凸轮机构的控制仿真 ** 目录 玩转Matlab-Simscape(初级)- 10 - 基于COMSOL&Simulink 凸轮机构的控制仿真 前言一、简介二、在Solidworks中创建3D模型ÿ…...

spark学习总结
系列文章目录 第1天总结:spark基础学习 1- Spark基本介绍(了解)2- Spark入门案例(掌握)3- 常见面试题(掌握) 文章目录 系列文章目录前言一、Spark基本介绍1、Spark是什么1.1 定义1.2 Spark与M…...

eNSP学习——帧中继基本配置
目录 主要命令 基本原理 实验目的 实验内容 实验拓扑 实验编址 实验步骤 1、基本配置 2、静态与动态映射的配置 3、子接口配置和静态路由 主要命令 [R1]int s1/0/0 [R1-Serial1/0/0]link-protocol fr //配置链路层协议为FR Warning: The encapsulation protocol…...
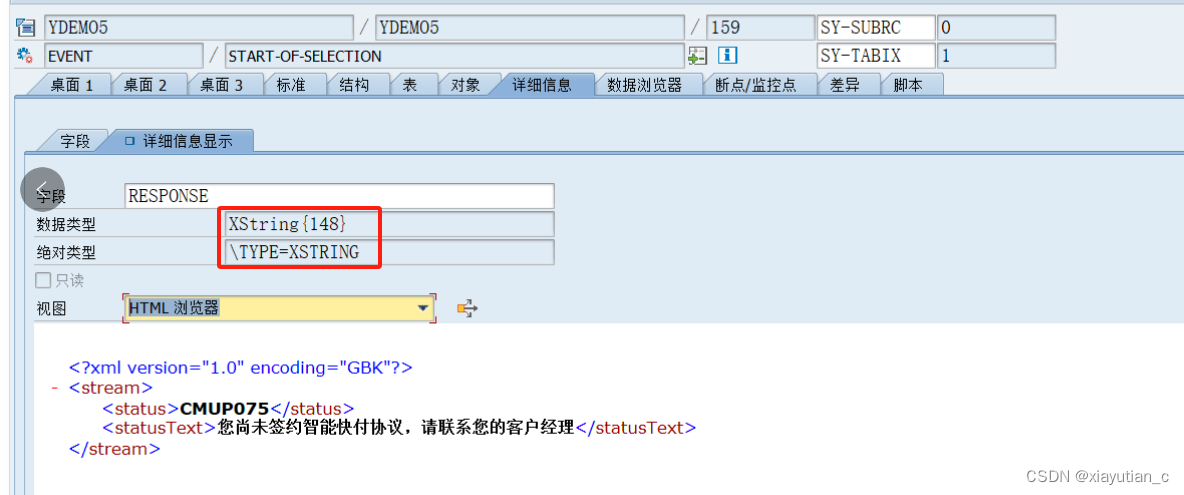
XML Encoding = ‘GBK‘ after STRANS,中文乱码
最近帮同事处理了一个中信银行银企直连接口的一个问题,同事反馈,使用STRANS转换XML后,encoding始终是’utf-16’,就算指定了GBK也不行。尝试了很多办法始终不行,发到银行的数据中,中文始终是乱码。 Debug使用HTML视图…...

【WiFi帧结构】
文章目录 帧结构MAC头部管理帧 帧结构 Wi-Fi的帧分为三部分组成:MAC头部frame bodyFCS,其中MAC是固定格式的,frame body是可变长度。 MAC头部有frame control,duration,address1,address2,addre…...

ssc377d修改flash分区大小
1、flash的分区默认分配16M、 / # df -h Filesystem Size Used Available Use% Mounted on /dev/root 1.9M 1.9M 0 100% / /dev/mtdblock4 3.0M...

pam_env.so模块配置解析
在PAM(Pluggable Authentication Modules)配置中, /etc/pam.d/su 文件相关配置含义如下: 配置解析 auth required pam_env.so1. 字段分解 字段值说明模块类型auth认证类模块,负责验证用户身份&am…...

[10-3]软件I2C读写MPU6050 江协科技学习笔记(16个知识点)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16...

2025 后端自学UNIAPP【项目实战:旅游项目】6、我的收藏页面
代码框架视图 1、先添加一个获取收藏景点的列表请求 【在文件my_api.js文件中添加】 // 引入公共的请求封装 import http from ./my_http.js// 登录接口(适配服务端返回 Token) export const login async (code, avatar) > {const res await http…...

Linux --进程控制
本文从以下五个方面来初步认识进程控制: 目录 进程创建 进程终止 进程等待 进程替换 模拟实现一个微型shell 进程创建 在Linux系统中我们可以在一个进程使用系统调用fork()来创建子进程,创建出来的进程就是子进程,原来的进程为父进程。…...

HarmonyOS运动开发:如何用mpchart绘制运动配速图表
##鸿蒙核心技术##运动开发##Sensor Service Kit(传感器服务)# 前言 在运动类应用中,运动数据的可视化是提升用户体验的重要环节。通过直观的图表展示运动过程中的关键数据,如配速、距离、卡路里消耗等,用户可以更清晰…...
安装docker)
Linux离线(zip方式)安装docker
目录 基础信息操作系统信息docker信息 安装实例安装步骤示例 遇到的问题问题1:修改默认工作路径启动失败问题2 找不到对应组 基础信息 操作系统信息 OS版本:CentOS 7 64位 内核版本:3.10.0 相关命令: uname -rcat /etc/os-rele…...

视觉slam十四讲实践部分记录——ch2、ch3
ch2 一、使用g++编译.cpp为可执行文件并运行(P30) g++ helloSLAM.cpp ./a.out运行 二、使用cmake编译 mkdir build cd build cmake .. makeCMakeCache.txt 文件仍然指向旧的目录。这表明在源代码目录中可能还存在旧的 CMakeCache.txt 文件,或者在构建过程中仍然引用了旧的路…...

根目录0xa0属性对应的Ntfs!_SCB中的FileObject是什么时候被建立的----NTFS源代码分析--重要
根目录0xa0属性对应的Ntfs!_SCB中的FileObject是什么时候被建立的 第一部分: 0: kd> g Breakpoint 9 hit Ntfs!ReadIndexBuffer: f7173886 55 push ebp 0: kd> kc # 00 Ntfs!ReadIndexBuffer 01 Ntfs!FindFirstIndexEntry 02 Ntfs!NtfsUpda…...
