Studying-代码随想录训练营day15| 222.完全二叉树的节点个数、110.平衡二叉树、257.二叉树的所有路径、404.左叶子之和
第十五天,二叉树part03💪,编程语言:C++
目录
257.完全二叉树的节点个数
110.平衡二叉树
257.二叉树的所有路径
404.左叶子之和
总结
257.完全二叉树的节点个数
文档讲解:代码随想录完全二叉树的节点个数
视频讲解:手撕完全二叉树的节点个数
题目:
学习:
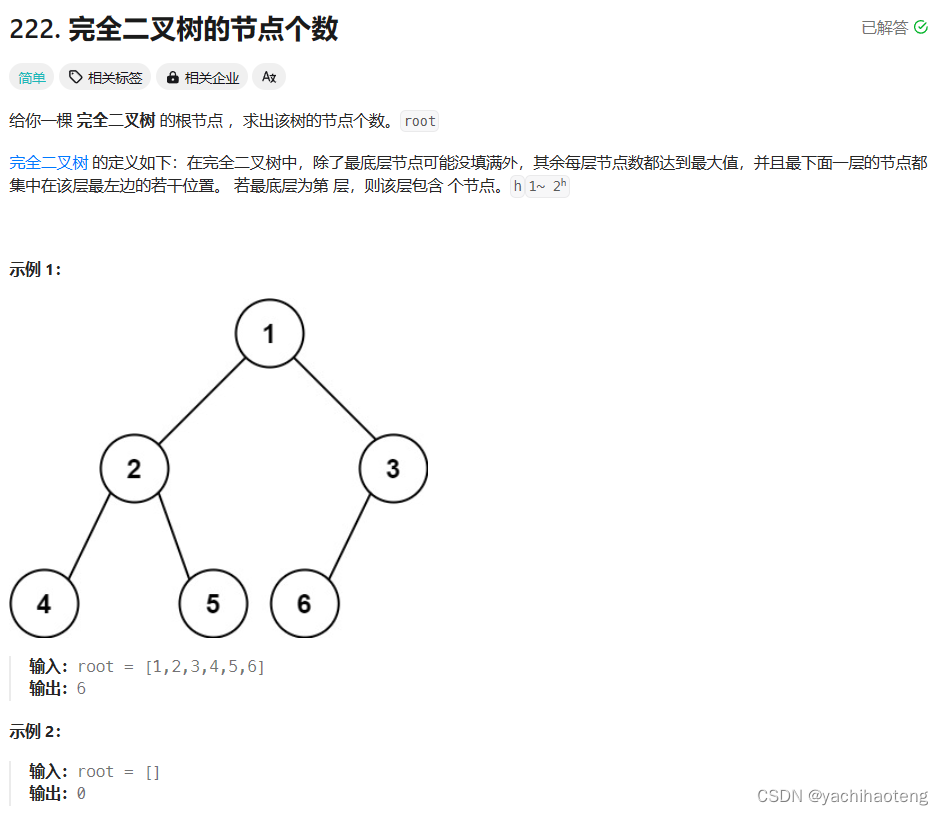
1. 根据完全二叉树的定义,我们可以把二叉树分为一个个满二叉树。满二叉树的定义为除叶子节点外,其余节点均含有左右两个孩子,此时节点的个数为2^height - 1;height就是这个满二叉树的高度。
2. 那如何确定是否是满二叉树呢,本题我们可以借助完全二叉树的定义,由于完全二叉树的特点,一个节点一定会先有它的左孩子,再有它的右孩子。因此倘若一棵树的一直往左遍历的深度,与一直往右遍历的深度相同,则说明这是一颗满二叉树,因为中间的节点一定是填满的,否则往右的深度一定时小于往左的深度。
3. 确定以上两点后,如何把一个二叉树分为一个个满二叉树。本题我们可以采用后序遍历的方法,在向下移动的过程中,我们可以每次判断该节点是否为一棵满二叉树的根节点(采用的方式就是2中所说的判断向左和向右的深度是否一样),如果是则可以通过满二叉树的式子直接返回该树的节点数,如果不是则继续往下。注意叶子节点在这也被我们看作成了一颗满二叉树,高度为1,节点个数为1。
代码:
//时间复杂度O(logn*logn)
//空间复杂度O(logn)
class Solution {
public:int countNodes(TreeNode* root) {//根节点为空,返回0//终止条件if (root == nullptr) return 0;TreeNode* left = root->left;TreeNode* right = root->right;int leftheight = 0; int rightheight = 0;while(left) {leftheight++;left = left->left;}while(right) {rightheight++;right = right->right;}//如果两边深度一样,则说明是一个完全二叉树,完全二叉树的节点数量为2^(leftheight + 1) - 1 if (leftheight == rightheight) return (2 << leftheight) - 1;//不满足终止条件的话,进入递归循环int leftnum = countNodes(root->left); //遍历左子树int rightnum = countNodes(root->right); //遍历右子树return 1 + leftnum + rightnum;}
};注意:本题也可以采用普通二叉树求节点数量的方式,采用层次遍历,时间复杂度为O(n)。
110.平衡二叉树
文档讲解:代码随想录平衡二叉树
视频讲解:手撕平衡二叉树
题目:
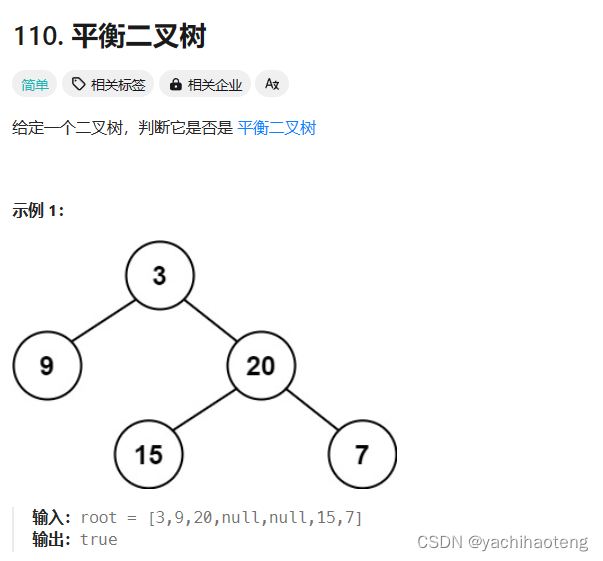
学习:平衡二叉树指的是,任意一个节点的左右子树的高度差不大于1。依据这个特点,我们可以采取后序遍历的方式,遍历每一个子树的高度,并且当存在一个子树的高度差大于2时,就可以立刻返回-1,不用继续遍历下去。
代码:
//时间复杂度O(n)
//空间复杂度O(n)
class Solution {
public://1.确定返回值,参数列表。//返回值:由于递归过程中需要比较左右子树的高度,所有返回值应该为int//参数:比较根节点左右子树的高度,因此只需要传入根节点即可int Height(TreeNode* root) {//2.确定终止条件、单层递归逻辑//①如果根节点为空,返回长度为0if (root == nullptr) return 0;//②如果已得知左子树不平衡,返回-1;int leftheight = Height(root->left);if (leftheight == -1) return -1;//③如果已得知右子树不平衡,返回-1;int rightheight = Height(root->right);if (rightheight == -1) return -1;return abs(leftheight - rightheight) > 1 ? -1 : (1 + max(leftheight, rightheight));} bool isBalanced(TreeNode* root) {if (Height(root) == -1) return false;return true;}
};注意:
- 此题不适合使用前序遍历,前序遍历一般用于求树的深度,是自顶向下的过程。 因此每次比较一个子树的深度时都需要遍历所有的子节点,时间复杂度会达到O(n^2)。后序遍历则不同,是自底向上的过程,在遍历的过程中,从底部开始比较,并把比较的结果不断往上传递,因此只需要遍历一遍节点即可。
- 此题也不适合使用迭代的方式,本题存在回溯比较的过程,使用迭代法会使得代码很复杂,且不利于实现回溯的过程,虽然递归一般来说都能用迭代来实现,但是也需要分析使用的场景。
257.二叉树的所有路径
文档讲解:二叉树的所有路径
视频讲解:手撕二叉树的所有路径
题目:
学习:
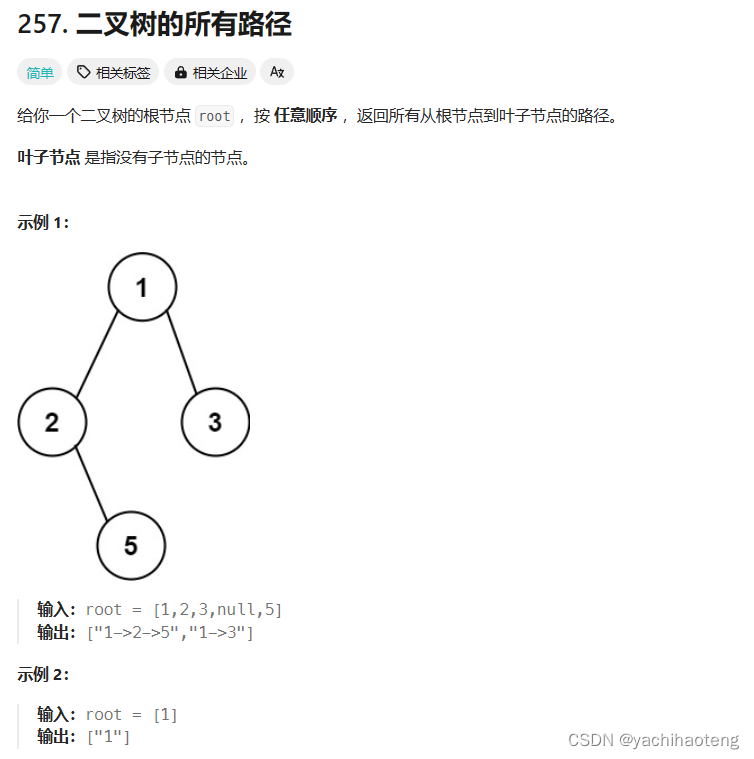
1. 本题要找到所有路径,因此必定需要遍历所有的节点,同时每条路径都是从根节点开始的,因此显然本题适合采用前序遍历来进行节点的遍历,遍历到下一个节点的时候,其父节点的信息就已经载入。
2. 同时本题存在大量的回溯过程,即找到一条路径后,要回到一个拐点(中间节点),再去寻找另一条路路径。回溯是下一章节的重点内容,其主要的实现方式就是递归实现,因此本题采用前序遍历的递归形式。
3. 本题在递归上有两个主要注意的点:①本题终止条件不再是找到空节点,而是找到叶子节点这条路径就可以终止了;②本题采用前序遍历,但是对节点的处理要放在终止条件判断前,因为每遍历到一个节点就需要把它加入到字符串当中。
代码:
//时间复杂度O(n^2)
//空间复杂度O(n^2)
class Solution {
public://注意path不能使用引用的方式,这种赋值的方式,不会改变传进来的值,因此会实现自动回溯void traversal(TreeNode* cur, string path, vector<string>& result) {path += to_string(cur->val); // 中,中为什么写在这里,因为最后一个节点也要加入到path中path += "->";if(cur->left == nullptr && cur->right == nullptr) {//把最后多余的箭头pop()掉path.pop_back();path.pop_back();result.push_back(path);}if(cur->left) { //左traversal(cur->left, path, result);}if(cur->right) { //右traversal(cur->right, path, result);}}vector<string> binaryTreePaths(TreeNode* root) {vector<string> result;traversal(root, "", result);return result;}
};注意:上面是使用了拷贝构造string path的方式,每一个递归拷贝了自己的一份path,以此来实现回溯过程。但也能够使用引用的方式,大家公用一份数组,但要注意此时需要自己进行回溯。
class Solution {
private:void traversal(TreeNode* cur, vector<int>& path, vector<string>& result) {path.push_back(cur->val); // 中,中为什么写在这里,因为最后一个节点也要加入到path中 // 这才到了叶子节点if (cur->left == NULL && cur->right == NULL) {string sPath;for (int i = 0; i < path.size() - 1; i++) {sPath += to_string(path[i]);sPath += "->";}sPath += to_string(path[path.size() - 1]);result.push_back(sPath);return;}if (cur->left) { // 左 traversal(cur->left, path, result);path.pop_back(); // 回溯}if (cur->right) { // 右traversal(cur->right, path, result);path.pop_back(); // 回溯}}public:vector<string> binaryTreePaths(TreeNode* root) {vector<string> result;vector<int> path;if (root == NULL) return result;traversal(root, path, result);return result;}
};总结:回溯的过程,实际上就是把上一个循环的所有数据环境保存下来,再回到上一个循环的时候,保证环境不变的过程。可以通过把递归放入栈中,体会回溯。
404.左叶子之和
文档讲解:代码随想录左叶子之和
视频讲解:手撕左叶子之和
题目:
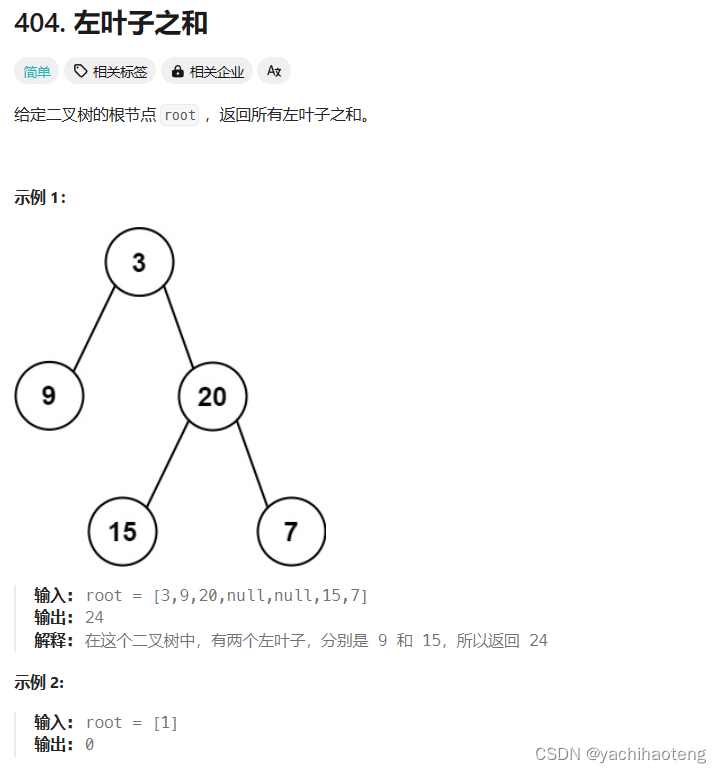
学习:本题需要找到所有的左叶子节点。左叶子节点的特点:1.是叶子节点,2.是父节点的左孩子。根据这两个特点来进行递归构造。
代码:前序遍历(递归)
//时间复杂度O(n)
//空间复杂度O(n)
class Solution {
public:// 1.确定返回值和参数列表,这里我们使用一个sum来计算总和,因此不需要返回值。void sumLeft(int& sum, TreeNode* root) {//左叶子节点的定义,1.是父节点的左节点,2.是叶子节点//2.确定终止条件if(root == nullptr) return;//其实这个也可以不写,如果不写不影响结果,但就会让递归多进行了一层。if(root->left == nullptr && root->right == nullptr) return;//3.确定单层递归逻辑//找到左叶子节点的父节点if(root->left != nullptr && root->left->left == nullptr && root->left->right == nullptr) {sum += root->left->val;}//如果没找到左叶子节点的父节点,则向下遍历sumLeft(sum, root->left);sumLeft(sum, root->right);}int sumOfLeftLeaves(TreeNode* root) {int sum = 0;sumLeft(sum, root);return sum;}
};注意:本题也可以采用后序遍历的方式。采用后序的遍历,返回值设为int型,从底部开始把左叶子节点的值累加并传递给父节点。
class Solution {
public:int sumOfLeftLeaves(TreeNode* root) {if (root == NULL) return 0;if (root->left == NULL && root->right== NULL) return 0;int leftValue = sumOfLeftLeaves(root->left); // 左if (root->left && !root->left->left && !root->left->right) { // 左子树就是一个左叶子的情况leftValue = root->left->val;}int rightValue = sumOfLeftLeaves(root->right); // 右int sum = leftValue + rightValue; // 中return sum;}
};
总结
今天的题重在对递归的使用,和对递归三大条件的设计上。
- 完全二叉树的节点个数:通过对递归条件终止条件的特殊处理,讲时间复杂度下降。
- 平衡二叉树:重点在于后序遍历求得树的高度,前序遍历求得树的深度,要根据需求进行选择。
- 二叉树的所有路径:重点在于对回溯的理解,要找到所有的路径,需要保存父节点的信息。同时由于每个节点遍历的时候就需要立马加入路径队列,因此还需要把对节点的处理放在终止条件的判断前。
- 左叶子之和:有两种不同的方法,根据左叶子节点的特点构造递归三部曲。
相关文章:

Studying-代码随想录训练营day15| 222.完全二叉树的节点个数、110.平衡二叉树、257.二叉树的所有路径、404.左叶子之和
第十五天,二叉树part03💪,编程语言:C 目录 257.完全二叉树的节点个数 110.平衡二叉树 257.二叉树的所有路径 404.左叶子之和 总结 257.完全二叉树的节点个数 文档讲解:代码随想录完全二叉树的节点个数 视频讲解…...

Python 基础:异常
目录 一、异常概念二、处理异常2.1 抛出异常2.2 使用 try-except 代码块2.3 使用 try-except-else 代码块2.4 静默失败 三、总结 遇到看不明白的地方,欢迎在评论中留言呐,一起讨论,一起进步! 本文参考:《Python编程&a…...

XML 应用程序
XML 应用程序 XML(可扩展标记语言)是一种用于存储和传输数据的标记语言。它是一种自我描述的语言,允许用户定义自己的标签和文档结构。XML广泛应用于各种应用程序中,包括网站开发、数据交换、文档管理等。本文将探讨XML的一些主要…...

SprringCloud Gateway动态添加路由不重启
文章目录 前言:一、动态路由必要性二、SpringCloud Gateway路由加载过程RouteDefinitionLocator接口PropertiesRouteDefinitionLocator类DiscoveryClientRouteDefinitionLocatorInMemoryRouteDefinitionRepositoryCompositeRouteDefinitionLocator类CachingRouteDef…...
Windows安装mysql
首先去官网下载社区版本的mysql(如果连不上,挂梯子) https://www.mysql.com/downloads/ 2. 去配置环境变量path 3. 在cmd里面初始化数据库(在搜索框输入cmd,或者在资源管理器下搜索烂输入cmd回车就行) my…...
chatgpt: linux 下用纯c 编写ui
在Linux下用纯C语言编写用户界面(UI),通常会使用GTK或Xlib。GTK是一个更高级的库,提供了丰富的控件和功能,而Xlib则是一个更底层的库,提供了直接操作X Window系统的功能。 下面是一个使用GTK在Linux上创建…...

Java十六进制Dump打印数据
代码 package test;import java.io.IOException;import sun.misc.HexDumpEncoder;@SuppressWarnings("restriction")...
某棋牌渗透测试
前言 由于传播、利用此文所提供的信息而造成的任何直接或者间接的后果及损失,均由使用者本人负责,文章作者不为此承担任何责任。 一、信息收集 这里通过fofa进行收集,语法为:body某棋牌 && titlexxx 图1-1 fofa资产收集 …...
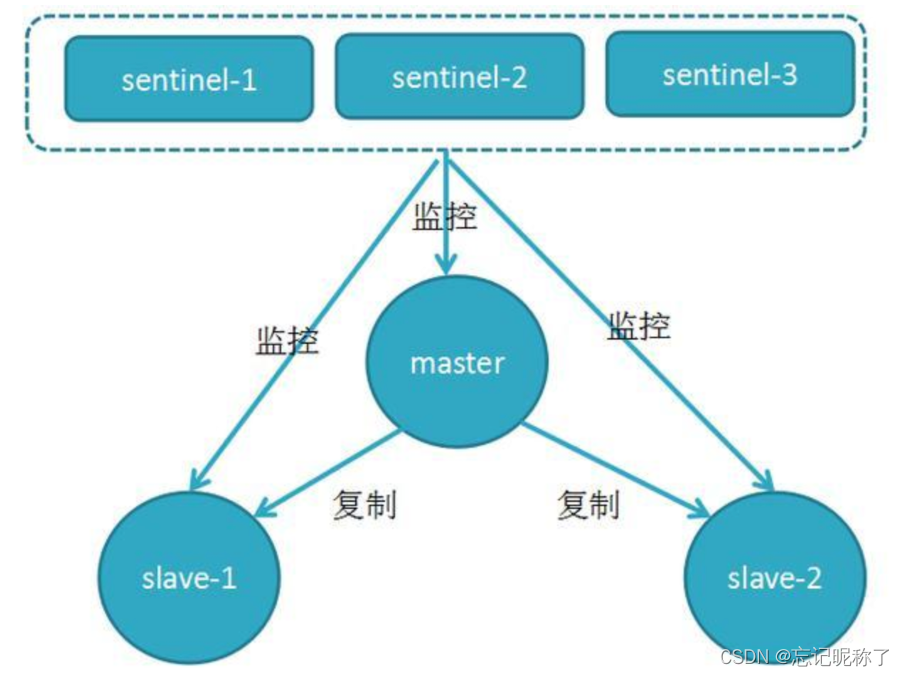
JAVA面试(六)
缓存 MemcachedredisRedis常见数据类型和使用Redis缓存持久化RDB-快照AOF-追加文件 Redis数据过期机制惰性删除定期删除Redis缓存淘汰策略(8种)算法LRU (Least Recently Used):最近最少使用LFU(Least Frequ…...

【C语言】手写学生管理系统丨附源码+教程
最近感觉大家好多在忙C语言课设~ 我来贡献一下,如果对你有帮助的话谢谢大家的点赞收藏喔! 1. 项目分析 小白的神级项目,99%的程序员,都做过这个项目! 掌握这个项目,就基本掌握 C 语言了! 跳…...

流媒体传输协议HTTP-FLV、WebSocket-FLV、HTTP-TS 和 WebSocket-TS的详细介绍、应用场景及对比
一、前言 HTTP-FLV、WS-FLV、HTTP-TS 和 WS-TS 是针对 FLV 和 TS 格式视频流的不同传输方式。它们通过不同的协议实现视频流的传输,以满足不同的应用场景和需求。接下来我们对这些流媒体传输协议进行剖析。 二、传输协议 1、HTTP-FLV 介绍:基于 HTTP…...

【机器学习】线性回归:从基础到实践的深度解析
🌈个人主页: 鑫宝Code 🔥热门专栏: 闲话杂谈| 炫酷HTML | JavaScript基础 💫个人格言: "如无必要,勿增实体" 文章目录 线性回归:从基础到实践的深度解析引言一、线性回归基础1.1 定义与目…...

短视频开源项目MoneyPrinterTurbo:AI副业搞起来,视频制作更轻松!
目录 引言一、MoneyPrinterTurbo简介二、MoneyPrinterTurbo的核心功能三、MoneyPrinterTurbo的未来发展四、MoneyPrinterTurbo与AI副业五、部署实践1、克隆代码2、创建虚拟环境3、安装依赖4、安装好 ImageMagick5、端口映射6、启动Web界面7、模型配置8、填写主题9、视频生成10、…...
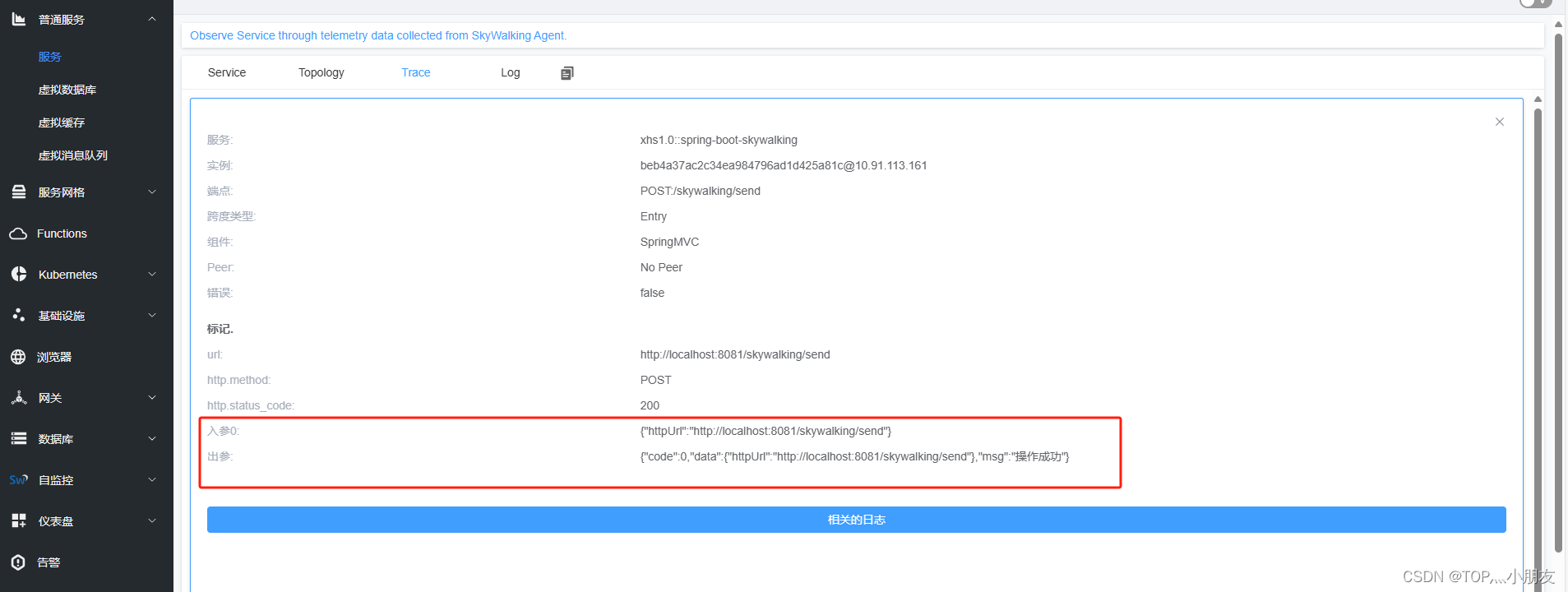
【JAVA】SpringBoot + skywalking 将接口的入参、出参、异常等信息上报到skywalking 链路追踪服务器上
【JAVA】SpringBoot skywalking 将接口的入参、出参、异常等信息上报到skywalking 链路追踪服务器上 1.下载SkyWalking APM https://skywalking.apache.org/downloads/ jdk8 不支持 SkyWalking APM 9.3.0以上版本,所以这里我们下载 9.3.0版本 2.下载 Java Agent …...

[xmake]构建静态库和动态库
xmake 静态库和动态库 在xmake中创建静态库和动态库的方法非常相似。以下是创建静态库和动态库的基本步骤: 创建xmake工程文件(xmake.lua)。 配置工程属性,包括工程名、版本等。 添加源代码文件到工程中。 设置是创建静态库还…...

功能测试 之 单模块测试----轮播图、登录、注册
单功能怎么测? 需求分析 拆解测试点 编写用例 1.轮播图 (1)需求分析 位置:后台--页面--广告管理---广告列表(搜索index页面增加广告位2) 操作完成后需要点击admin---更新缓存,前台页面刷新生效 (2)拆解…...

MyBatis-PageHelper 源码解说
归档 GitHub: MyBatis-PageHelper-源码解说 总说明 源码仓库: https://github.com/pagehelper/Mybatis-PageHelper克隆:git clone https://github.com/pagehelper/Mybatis-PageHelper.git切分支(tag):git checkout m…...

基于uni-app和图鸟UI的智慧校园圈子小程序开发实践
摘要: 随着教育信息化和“互联网教育”的快速发展,智慧校园建设已成为推动校园管理现代化、提高教育教学质量的重要手段。本文介绍了基于uni-app和图鸟UI开发的智慧校园圈子小程序,旨在通过一站式服务、个性化定制、数据互通和安全可靠等特点…...

STM32 keil工程移植到Visual Studio Code环境中编译
1、GCC Vscode 搭建 STM32 开发环境 GCC Vscode 搭建 STM32 开发环境(一)- 环境部署 - 知乎 (zhihu.com) 2、在原有keil工程下找到原本CUBEMX生成的.ioc工程文件 3、将.ioc文件复制一个新的文件夹下双击打开工程,将IDE选为Makefile&…...

细说CountDownLatch
CountDownLatch是Java中提供的一个同步辅助类,它允许一个或多个线程等待其他线程完成操作。在面试中,面试官经常会询问候选人是否在实际项目中使用过CountDownLatch,以评估其对多线程编程和并发控制的理解和经验。本文将详细介绍CountDownLat…...

手游刚开服就被攻击怎么办?如何防御DDoS?
开服初期是手游最脆弱的阶段,极易成为DDoS攻击的目标。一旦遭遇攻击,可能导致服务器瘫痪、玩家流失,甚至造成巨大经济损失。本文为开发者提供一套简洁有效的应急与防御方案,帮助快速应对并构建长期防护体系。 一、遭遇攻击的紧急应…...

Flask RESTful 示例
目录 1. 环境准备2. 安装依赖3. 修改main.py4. 运行应用5. API使用示例获取所有任务获取单个任务创建新任务更新任务删除任务 中文乱码问题: 下面创建一个简单的Flask RESTful API示例。首先,我们需要创建环境,安装必要的依赖,然后…...

label-studio的使用教程(导入本地路径)
文章目录 1. 准备环境2. 脚本启动2.1 Windows2.2 Linux 3. 安装label-studio机器学习后端3.1 pip安装(推荐)3.2 GitHub仓库安装 4. 后端配置4.1 yolo环境4.2 引入后端模型4.3 修改脚本4.4 启动后端 5. 标注工程5.1 创建工程5.2 配置图片路径5.3 配置工程类型标签5.4 配置模型5.…...

LLM基础1_语言模型如何处理文本
基于GitHub项目:https://github.com/datawhalechina/llms-from-scratch-cn 工具介绍 tiktoken:OpenAI开发的专业"分词器" torch:Facebook开发的强力计算引擎,相当于超级计算器 理解词嵌入:给词语画"…...

mac 安装homebrew (nvm 及git)
mac 安装nvm 及git 万恶之源 mac 安装这些东西离不开Xcode。及homebrew 一、先说安装git步骤 通用: 方法一:使用 Homebrew 安装 Git(推荐) 步骤如下:打开终端(Terminal.app) 1.安装 Homebrew…...
)
安卓基础(Java 和 Gradle 版本)
1. 设置项目的 JDK 版本 方法1:通过 Project Structure File → Project Structure... (或按 CtrlAltShiftS) 左侧选择 SDK Location 在 Gradle Settings 部分,设置 Gradle JDK 方法2:通过 Settings File → Settings... (或 CtrlAltS)…...

Python实现简单音频数据压缩与解压算法
Python实现简单音频数据压缩与解压算法 引言 在音频数据处理中,压缩算法是降低存储成本和传输效率的关键技术。Python作为一门灵活且功能强大的编程语言,提供了丰富的库和工具来实现音频数据的压缩与解压。本文将通过一个简单的音频数据压缩与解压算法…...

【Linux】Linux安装并配置RabbitMQ
目录 1. 安装 Erlang 2. 安装 RabbitMQ 2.1.添加 RabbitMQ 仓库 2.2.安装 RabbitMQ 3.配置 3.1.启动和管理服务 4. 访问管理界面 5.安装问题 6.修改密码 7.修改端口 7.1.找到文件 7.2.修改文件 1. 安装 Erlang 由于 RabbitMQ 是用 Erlang 编写的,需要先安…...

Spring Boot + MyBatis 集成支付宝支付流程
Spring Boot MyBatis 集成支付宝支付流程 核心流程 商户系统生成订单调用支付宝创建预支付订单用户跳转支付宝完成支付支付宝异步通知支付结果商户处理支付结果更新订单状态支付宝同步跳转回商户页面 代码实现示例(电脑网站支付) 1. 添加依赖 <!…...
)
stm32进入Infinite_Loop原因(因为有系统中断函数未自定义实现)
这是系统中断服务程序的默认处理汇编函数,如果我们没有定义实现某个中断函数,那么当stm32产生了该中断时,就会默认跑这里来了,所以我们打开了什么中断,一定要记得实现对应的系统中断函数,否则会进来一直循环…...
