双层循环和循环语句
echo 打印
echo -n 表示不换行输出
echo -e 表示输出转义字符
echo \b 相当于退格键(backspace)
echo \n 换行,相当于回车
echo \f 换行,换行后的新行的开头连着上一行的行尾
echo \t 相当于tab健 (横向制表符 )
echo -ne 制表符(相当于列表格)
while 和 until的语法
while满足条件就执行循环,不满足条件才会退出
死循环,不知道循环多少次,需要主动结束循环或者达到条件才结束循环
while格式:
while [判断条件]
do
命令序列
done
双层循环 (内循环是列 外循环是行)




反过来

break 1就是里面跳出循环,2就是里外都跳出循环(先执行里面在外面也一起跳出)
continue 1 就是里面跳 ,2就是里面先跳出然后从外面重新继续执行

continue

while
1-100求和

1-100的奇数和、偶数和

until
条件不成立才执行命令

打印/opt目录下所有的文件包括目录
测试网段(工作需要用到)

做一个简单的计算器
创建密码锁定
相关文章:

双层循环和循环语句
echo 打印 echo -n 表示不换行输出 echo -e 表示输出转义字符 echo \b 相当于退格键(backspace) echo \n 换行,相当于回车 echo \f 换行,换行后的新行的开头连着上一行的行尾 echo \t 相当于tab健 (…...

【Codesys】-计算开机通电运行时间,累计正常使用时间,故障停机时间
应客户要求,在程序添加了这个用来计算开机运行时间,原理就是取当前时间减去一开始记录的时间,没什么特别要求,记录一下使用的变量类型和数据写法,防止忘记了。 下文只写了一个开机通电运行时间的写法,累计…...

LINUX系统编程:线程的概念
目录 1.线程的概念 2.线程的理解 3.怎么做到划分代码的 本文主要介绍,在LIUNX下的线程。 1.线程的概念 在很多的书上的你可能见过这样的。 线程是进程内部的一个执行分支,线程是cpu调度的基本单位。 加载到内存的程序叫做进程。修正:进…...

如何更换OpenHarmony SDK API 10
OpenHarmony社区已经发布OpenHarmony SDK API 10 beta版本,有些 Sample案例 也有需要API10。那么如何替换使用新的OpenHarmony SDK API 10呢?本文做个记录。 1、如何获取OpenHarmony SDK 1.1 每日构建流水线 可以从OpenHarmony每日构建站点获取最新的…...

Java | Leetcode Java题解之第155题最小栈
题目: 题解: class MinStack {Deque<Integer> xStack;Deque<Integer> minStack;public MinStack() {xStack new LinkedList<Integer>();minStack new LinkedList<Integer>();minStack.push(Integer.MAX_VALUE);}public void …...
大润发超市购物卡怎么用?
收到大润发超市的礼品卡以后,我才发现,最近的大润发也得十来公里 为了100块的大润发打车也太不划算了 叫外送也不在配送范围内 最后没办法,在收卡云上出掉了,还好最近价格不错,也不亏,收卡云的到账速度也…...
【ai】tx2-nx:搭配torch的torchvision
微雪的教程pytorch_version 1.10.0 官方教程安装torch官方教程 依赖项 nvidia@tx2-nx:~/twork/03_yolov5$ $ sudo apt-get install libjpeg-dev zlib1g-dev lib...

深入浅出MyBatis:全面解析与实战指南
MyBatis 是一个优秀的持久层框架,它简化了 Java 应用与关系数据库之间的映射。对于大多数 Java 开发者而言,掌握 MyBatis 是必不可少的一部分。本文将详细介绍 MyBatis 的各个方面,包括其基本原理、配置、操作、动态 SQL、插件机制和高级应用…...
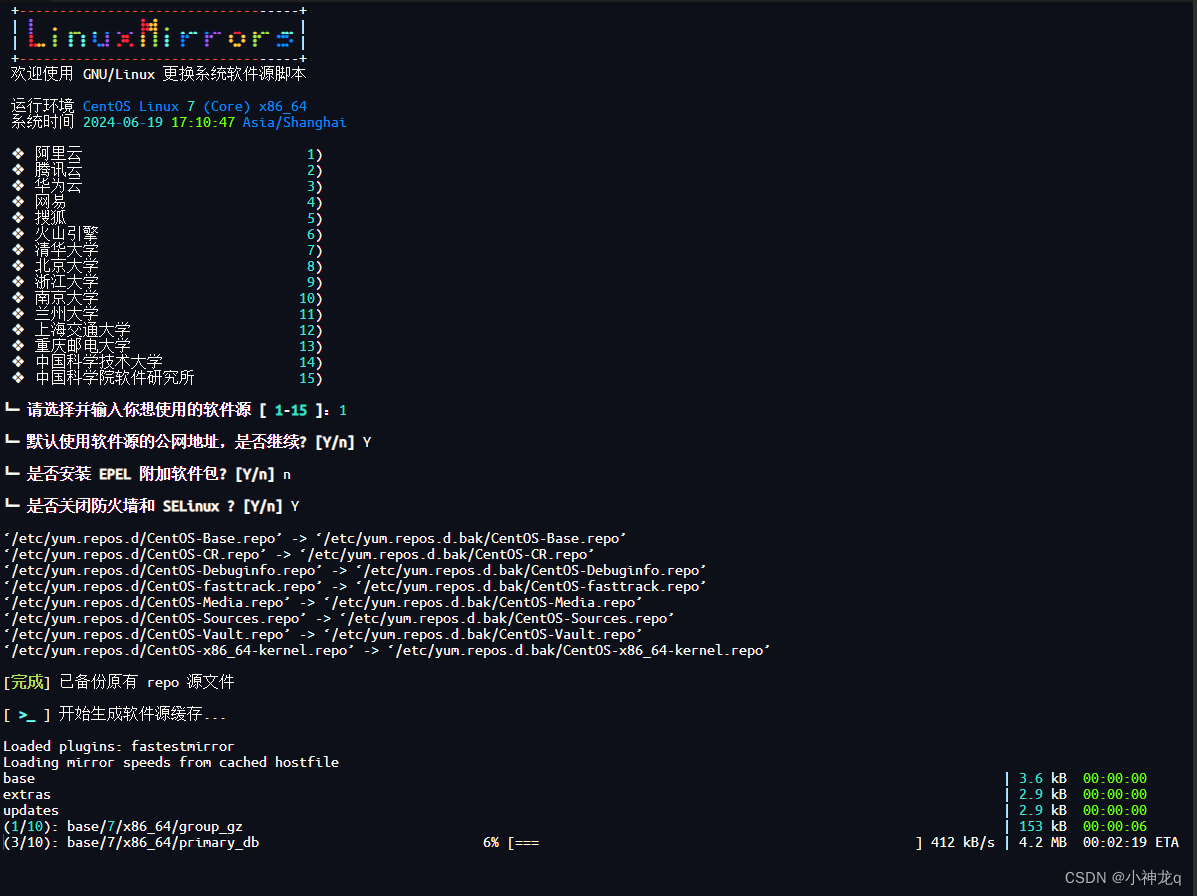
好用的linux一键换源脚本
最近发现一个好用的linux一键换源脚本,记录一下 官方链接 大陆使用 bash <(curl -sSL https://linuxmirrors.cn/main.sh)# github地址 bash <(curl -sSL https://raw.githubusercontent.com/SuperManito/LinuxMirrors/main/ChangeMirrors.sh) # gitee地址 …...

机器人----控制方式
位置控制 点位控制 点到点--PTP 只关心起点和目标点,不关心走过的轨迹。 连续轨迹控制 CP(continus path) eg:焊接,切割。 力控制 使用多大的力进行控制。 eg:用多大的力写字。...

json的特点
JJSON是一种轻量级的数据交换格式,它基于JavaScript编程语言的一个子集,采用完全独立于语言的文本格式,结构化程度高。 JSON的主要特点包括: 轻量级:JSON的格式紧凑,易于传输和解析。 结构化:…...
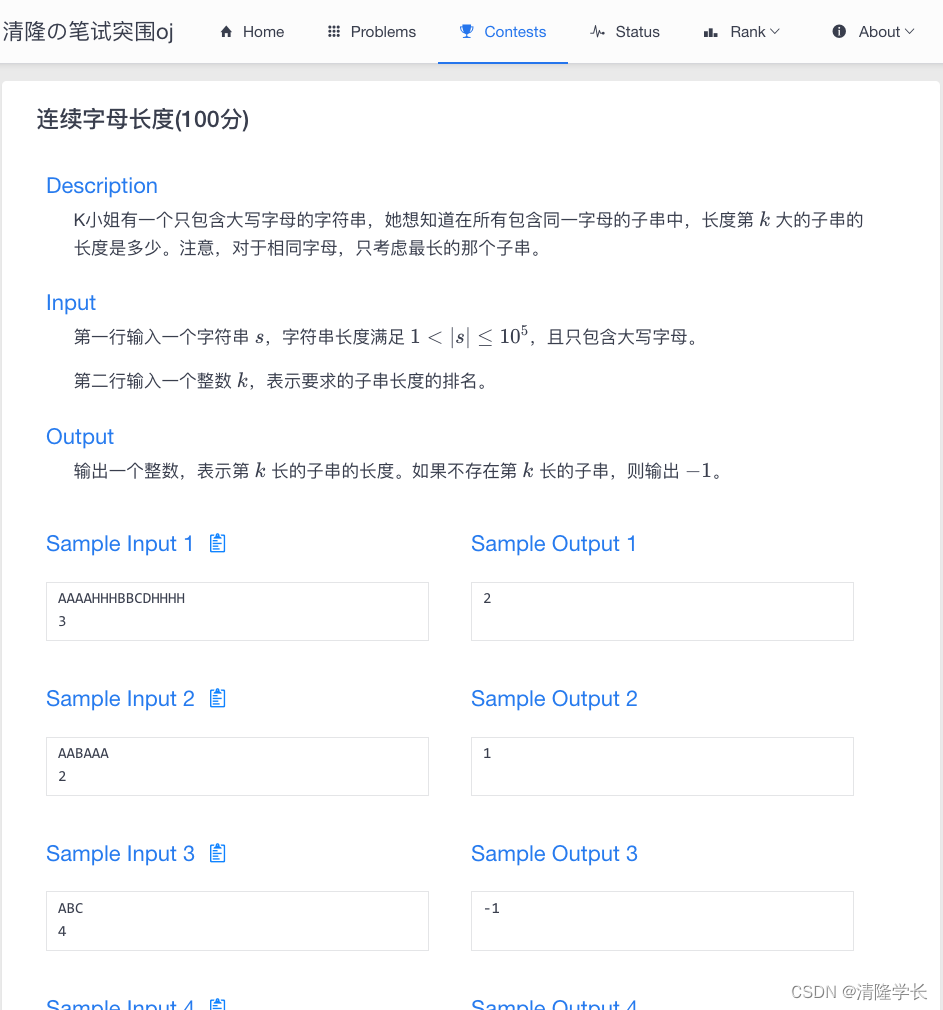
【2024最新华为OD-C/D卷试题汇总】[支持在线评测] 连续字母长度(100分) - 三语言AC题解(Python/Java/Cpp)
🍭 大家好这里是清隆学长 ,一枚热爱算法的程序员 ✨ 本系列打算持续跟新华为OD-C/D卷的三语言AC题解 💻 ACM银牌🥈| 多次AK大厂笔试 | 编程一对一辅导 👏 感谢大家的订阅➕ 和 喜欢💗 …...

18 Shell编程规范与变量
目录 18.1 Shell脚本概述 18.1.1 Shell的作用 18.1.2 编写第一个Shell脚本 18.1.3 重定向与管道操作 18.2 Shell变量的作用、类型 18.2.1 自定义变量 18.2.2 特殊的Shell变量 18.1 Shell脚本概述 可以批量处理、自动化地完成一系列维护任务,大大减轻管理员的负担。…...
Linux基础命令大全(详解版)
Linux基础命令(详解版) 文章目录 Linux基础命令(详解版)1.Linux的目录结构**2.Linux路径的描述方式**3.Linux命令基础格式4.ls命令 隐藏文件、文件夹5.pwd命令6.cd命令 特殊路径符7.mkdir命令 文件操作命令8.touch命令9.cat命令10…...

python列表常见去重方法
列表去重在python实际运用中,十分常见,也是最基础的重点知识。 1. 使用for循环实现列表去重 此方法去重后,原顺序保持不变。 # for循环实现列表去重 list1 [a, 4, 6, 4, b, hello, hello, world, 9, 9, 4, a] list2 [] for l1 in list1:…...

usb摄像头应用编程
作者简介: 一个平凡而乐于分享的小比特,中南民族大学通信工程专业研究生在读,研究方向无线联邦学习 擅长领域:驱动开发,嵌入式软件开发,BSP开发 作者主页:一个平凡而乐于分享的小比特的个人主页…...
康谋分享 | 自动驾驶联合仿真——功能模型接口FMI(一)
功能模型接口FMI(Functional Mock-up Interface)是一个开放且与工具解耦的标准。FMI包含了一个C-API(接口),一个用于描述接口的XML文件以及可交换的功能模型单元FMU(Functional Mock-up Unit)&a…...

OPenCV中绘制多条多边形曲线函数polylines的使用
操作系统:ubuntu22.04OpenCV版本:OpenCV4.9IDE:Visual Studio Code编程语言:C11 功能描述 绘制多条多边形曲线 原型1 void cv::polylines ( InputOutputArray img, InputArrayOfArrays pts, bool isClosed, const Scalar & color…...

气膜球幕影院:娱乐体验的新高度—轻空间
气膜球幕影院以其独特的全景沉浸体验和丰富的娱乐内容,成为了现代娱乐产业的重要组成部分。轻空间带您来探索一下气膜球幕影院带来的独特娱乐体验。 全景沉浸式体验 气膜球幕影院的360度全景沉浸式体验,彻底改变了传统观影方式。观众被包围在一个球形屏幕…...
阿里CEO个人投资的智驾公司,走了不一样的路
佑驾创新在去年8月和11月完成两轮融资,在今年5月底递表港交所,目前拿到了29家车企88款车型的量产订单。自动驾驶赛道不缺明星,这些因素本不足以凸显它的差异化。但是在招股书中,一条特殊的发展路线,却让佑驾创新显得不…...

Flask RESTful 示例
目录 1. 环境准备2. 安装依赖3. 修改main.py4. 运行应用5. API使用示例获取所有任务获取单个任务创建新任务更新任务删除任务 中文乱码问题: 下面创建一个简单的Flask RESTful API示例。首先,我们需要创建环境,安装必要的依赖,然后…...

【CSS position 属性】static、relative、fixed、absolute 、sticky详细介绍,多层嵌套定位示例
文章目录 ★ position 的五种类型及基本用法 ★ 一、position 属性概述 二、position 的五种类型详解(初学者版) 1. static(默认值) 2. relative(相对定位) 3. absolute(绝对定位) 4. fixed(固定定位) 5. sticky(粘性定位) 三、定位元素的层级关系(z-i…...

【论文笔记】若干矿井粉尘检测算法概述
总的来说,传统机器学习、传统机器学习与深度学习的结合、LSTM等算法所需要的数据集来源于矿井传感器测量的粉尘浓度,通过建立回归模型来预测未来矿井的粉尘浓度。传统机器学习算法性能易受数据中极端值的影响。YOLO等计算机视觉算法所需要的数据集来源于…...

Python爬虫(一):爬虫伪装
一、网站防爬机制概述 在当今互联网环境中,具有一定规模或盈利性质的网站几乎都实施了各种防爬措施。这些措施主要分为两大类: 身份验证机制:直接将未经授权的爬虫阻挡在外反爬技术体系:通过各种技术手段增加爬虫获取数据的难度…...

全面解析各类VPN技术:GRE、IPsec、L2TP、SSL与MPLS VPN对比
目录 引言 VPN技术概述 GRE VPN 3.1 GRE封装结构 3.2 GRE的应用场景 GRE over IPsec 4.1 GRE over IPsec封装结构 4.2 为什么使用GRE over IPsec? IPsec VPN 5.1 IPsec传输模式(Transport Mode) 5.2 IPsec隧道模式(Tunne…...

DeepSeek 技术赋能无人农场协同作业:用 AI 重构农田管理 “神经网”
目录 一、引言二、DeepSeek 技术大揭秘2.1 核心架构解析2.2 关键技术剖析 三、智能农业无人农场协同作业现状3.1 发展现状概述3.2 协同作业模式介绍 四、DeepSeek 的 “农场奇妙游”4.1 数据处理与分析4.2 作物生长监测与预测4.3 病虫害防治4.4 农机协同作业调度 五、实际案例大…...

GitFlow 工作模式(详解)
今天再学项目的过程中遇到使用gitflow模式管理代码,因此进行学习并且发布关于gitflow的一些思考 Git与GitFlow模式 我们在写代码的时候通常会进行网上保存,无论是github还是gittee,都是一种基于git去保存代码的形式,这样保存代码…...

FFmpeg:Windows系统小白安装及其使用
一、安装 1.访问官网 Download FFmpeg 2.点击版本目录 3.选择版本点击安装 注意这里选择的是【release buids】,注意左上角标题 例如我安装在目录 F:\FFmpeg 4.解压 5.添加环境变量 把你解压后的bin目录(即exe所在文件夹)加入系统变量…...

(一)单例模式
一、前言 单例模式属于六大创建型模式,即在软件设计过程中,主要关注创建对象的结果,并不关心创建对象的过程及细节。创建型设计模式将类对象的实例化过程进行抽象化接口设计,从而隐藏了类对象的实例是如何被创建的,封装了软件系统使用的具体对象类型。 六大创建型模式包括…...

Web后端基础(基础知识)
BS架构:Browser/Server,浏览器/服务器架构模式。客户端只需要浏览器,应用程序的逻辑和数据都存储在服务端。 优点:维护方便缺点:体验一般 CS架构:Client/Server,客户端/服务器架构模式。需要单独…...
