二叉树的这五种遍历方法你们都会了吗?
说在前面
🎈二叉树大家应该都很熟了吧,那二叉树的这五种遍历方式你们都会了吗?
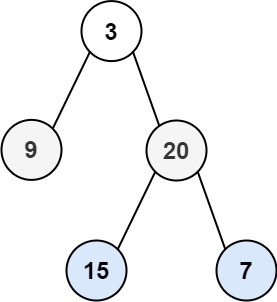
以这一二叉树为例子,我们来看看不同遍历方式返回的结果都是怎样的。
前序遍历
前序遍历的顺序是:首先访问根节点,然后递归地遍历左子树,最后递归地遍历右子树。
var preorderTraversal = function(root) {const res = [];const traversal = (r)=>{if (r === null) return;res.push(r.val); // 访问根节点traversal(r.left); // 遍历左子树traversal(r.right); // 遍历右子树};traversal(root);return res;
};
- 输出结果
[3,9,20,15,7]
中序遍历
中序遍历的顺序是:首先递归地遍历左子树,然后访问根节点,最后递归地遍历右子树。
var inorderTraversal = function(root) {const res = [];const traversal = (r)=>{if (r === null) return;traversal(r.left); // 遍历左子树res.push(r.val); // 访问根节点traversal(r.right); // 遍历右子树};traversal(root);return res;
};
- 输出结果
[9,3,15,20,7]
后序遍历
后序遍历的顺序是:首先递归地遍历左子树,然后递归地遍历右子树,最后访问根节点。
var postorderTraversal = function(root) {const res = [];const traversal = (r)=>{if (r === null) return;traversal(r.left); // 遍历左子树traversal(r.right); // 遍历右子树res.push(r.val); // 访问根节点};traversal(root);return res;
};
- 输出结果
[9,15,7,20,3]
层序遍历
层序遍历按照从上到下、从左到右的顺序访问二叉树的所有节点。
以广度优先策略遍历节点的方法:
- 使用队列作为辅助数据结构。
- 按照节点的深度层次访问二叉树,从根节点开始,逐层向下。
var levelOrderTraversal = function(root) {const res = [];const queue = [root];if(!root) return [];while(queue.length > 0){const node = queue.shift();res.push(node.val);node.left && queue.push(node.left);node.right && queue.push(node.right);}return res;
};
- 输出结果
[3,9,20,15,7]
垂序遍历
对位于 (row, col) 的每个结点而言,其左右子结点分别位于 (row + 1, col - 1) 和 (row + 1, col + 1) 。树的根结点位于 (0, 0) 。
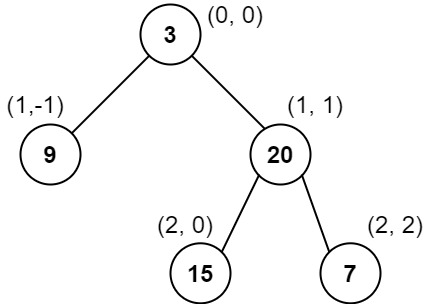
二叉树的 垂序遍历 从最左边的列开始直到最右边的列结束,按列索引每一列上的所有结点,形成一个按出现位置从上到下排序的有序列表。如果同行同列上有多个结点,则按结点的值从小到大进行排序。
在层序遍历的基础上记录每个数据所在的位置再重新进行排序即可。
var verticalTraversal = function (root) {const nodeList = [];const q = [{ node: root, row: 0, col: 0 }];//获取二叉树节点集合while (q.length) {const { node, row, col } = q.shift();nodeList.push({ val: node.val, row: row, col });if (node.left) q.push({ node: node.left, row: row - 1, col: col + 1 });if (node.right) q.push({ node: node.right, row: row + 1, col: col + 1 });}//对二叉树节点进行排序nodeList.sort((a, b) => {if (a.row === b.row && a.col === b.col) {return a.val - b.val;}return a.row - b.row;});//对二叉树节点进行分组const res = [[nodeList[0].val]];for (let i = 1; i < nodeList.length; i++) {if (nodeList[i].row !== nodeList[i - 1].row) {res.push([]);}res[res.length - 1].push(nodeList[i].val);}return res;
};
- 输出结果
[[9],[3,15],[20],[7]]
公众号
关注公众号『前端也能这么有趣』,获取更多有趣内容。
说在后面
🎉 这里是 JYeontu,现在是一名前端工程师,有空会刷刷算法题,平时喜欢打羽毛球 🏸 ,平时也喜欢写些东西,既为自己记录 📋,也希望可以对大家有那么一丢丢的帮助,写的不好望多多谅解 🙇,写错的地方望指出,定会认真改进 😊,偶尔也会在自己的公众号『
前端也能这么有趣』发一些比较有趣的文章,有兴趣的也可以关注下。在此谢谢大家的支持,我们下文再见 🙌。
相关文章:

二叉树的这五种遍历方法你们都会了吗?
说在前面 🎈二叉树大家应该都很熟了吧,那二叉树的这五种遍历方式你们都会了吗? 以这一二叉树为例子,我们来看看不同遍历方式返回的结果都是怎样的。 前序遍历 前序遍历的顺序是:首先访问根节点,然后递归地…...

使用模数转换器的比例电阻测量基础知识
A/D 转换器是比率式的,也就是说,它们的结果与输入电压与参考电压的比值成正比。这可用于简化电阻测量。 测量电阻的标准方法是让电流通过电阻并测量其压降 (见图 1)。然后,欧姆定律(V I x R) 可用于计算电压和电流的…...

(C++语言的设计和演化) C++的设计理念
文章目录 前言📖C 语言设计规则📐规则和原理📐一般性规则📐设计支持规则📐语言的技术性规则📐低级程序设计支持规则 📖标准化(扩充评判准则)📐它精确吗&#…...

AI音乐:创新引擎还是创意终结者?
✨作者主页: Mr.Zwq✔️个人简介:一个正在努力学技术的Python领域创作者,擅长爬虫,逆向,全栈方向,专注基础和实战分享,欢迎咨询! 您的点赞、关注、收藏、评论,是对我最大…...

20240621每日后端---------如何优化项目中的10000个if-else 语句?
如何优化 10000 个 if-else 语句?有没有好的解决方案? 额,本身问题就很奇怪,怎么可能有这种代码。。。世界你让我陌生,但是我们还是假象着看看能不能解决一下。 解决方案1:策略模式 使用策略模式确实可以…...
【STM32】时钟树系统
1.时钟树简介 1.1五个时钟源 LSI是低速内部时钟,RC振荡器,频率为32kHz左右。供独立看门狗和自动唤醒单元使用。 LSE是低速外部时钟,接频率为32.768kHz的石英晶体。这个主要是RTC的时钟源。 HSE是高速外部时钟,可接石英*/陶瓷谐振…...
docker换源
文章目录 前言1. 查找可用的镜像源2. 配置 Docker 镜像源3. 重启 Docker 服务4. 查看dock info是否修改成功5. 验证镜像源是否更换成功注意事项 前言 在pull镜像时遇到如下报错: ┌──(root㉿kali)-[/home/longl] └─# docker pull hello-world Using default …...
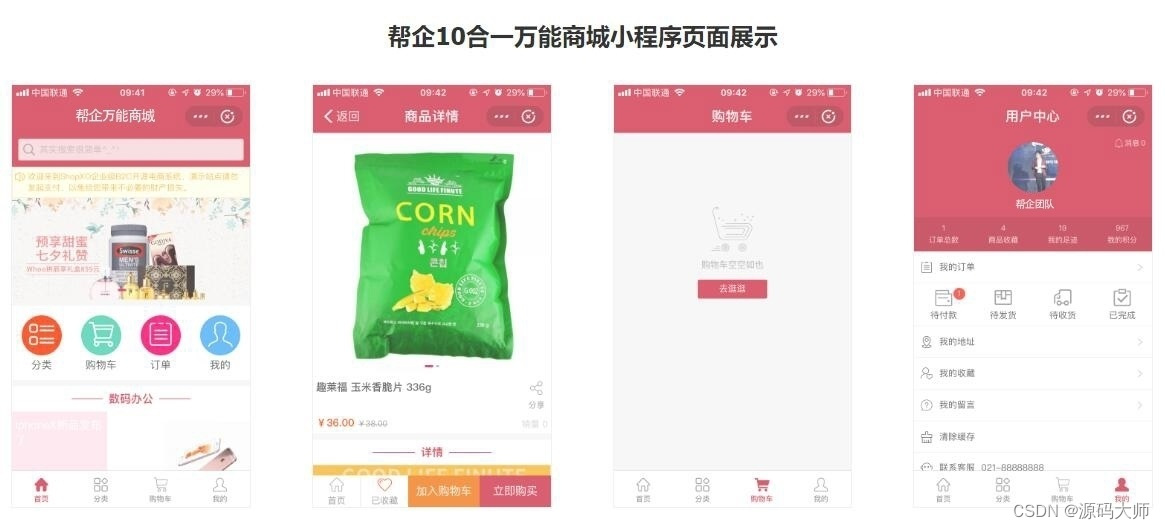
百度在线分销商城小程序源码系统 分销+会员组+新用户福利 前后端分离 带完整的安装代码包以及搭建部署教程
系统概述 百度在线分销商城小程序源码系统是一款集分销、会员组管理和新用户福利于一体的前后端分离的系统。它采用先进的技术架构,确保系统的稳定性、高效性和安全性。该系统的前端基于小程序开发,为用户提供了便捷的购物体验和交互界面。用户可以通过…...

Flutter【组件】富文本组件
简介 flutter 富文本组件。 github地址: https://github.com/ThinkerJack/jac_uikit pub地址:https://pub.dev/packages/jac_uikit 使用方式 运行 flutter pub add jac_uikit组件文档 使用方式: HighlightedTextWidget.builder(text: &…...

中国恋爱交友相亲软件有哪些?大型婚恋相亲交友APP真实测评推荐
嘿嘿,当了29年的单身汪,这下总算不再单着啦!这两年把身边能找的人都找遍了,也没碰到合适的。没办法,就跑到网上去试试,坚持了有半年,可算有对象啦!下面给大家说说我用过的几个能脱单…...
快速欧氏聚类与普通欧氏聚类比较
1、前言 文献《FEC: Fast Euclidean Clustering for Point Cloud Segmentation》介绍了一种快速欧氏聚类方法,大概原理可以参考如下图,具体原理可以参考参考文献。 2、时间效率比较:快速欧氏聚类VS普通欧氏聚类 网上搜集的快速欧式聚类,与自己手写的普通欧式聚类进行对比,…...

如何让大语言模型在规格普通的硬件上运行 - 量化技术
近年来,大型语言模型(LLMs)的能力有了飞跃式的发展,使其在越来越多的应用场景中更加友好和适用。然而,随着LLMs的智能和复杂度的增加,其参数数量,即权重和激活值的数量也在增加,这意…...

shell printf详解
默认的 printf 不会像 echo 自动添加换行符,我们可以手动添加 \n。 1. printf命令语法组成: printg format-string [arguments] 第一部分为格式化字符串,该字符串最好用引号括起来 第二部分为参数列表,例如字符串或变量值的列表,该列表需…...

【数据分析】用Python做事件抽取任务-快速上手方案
目录 方法一:使用OmniEvent库安装OmniEvent使用OmniEvent进行事件抽取OmniEvent优点缺点 方法二:使用大模型使用GPT网页版进行事件抽取事件类型列表 大模型优点缺点 总结 在自然语言处理(NLP)领域,事件抽取是一项关键任…...
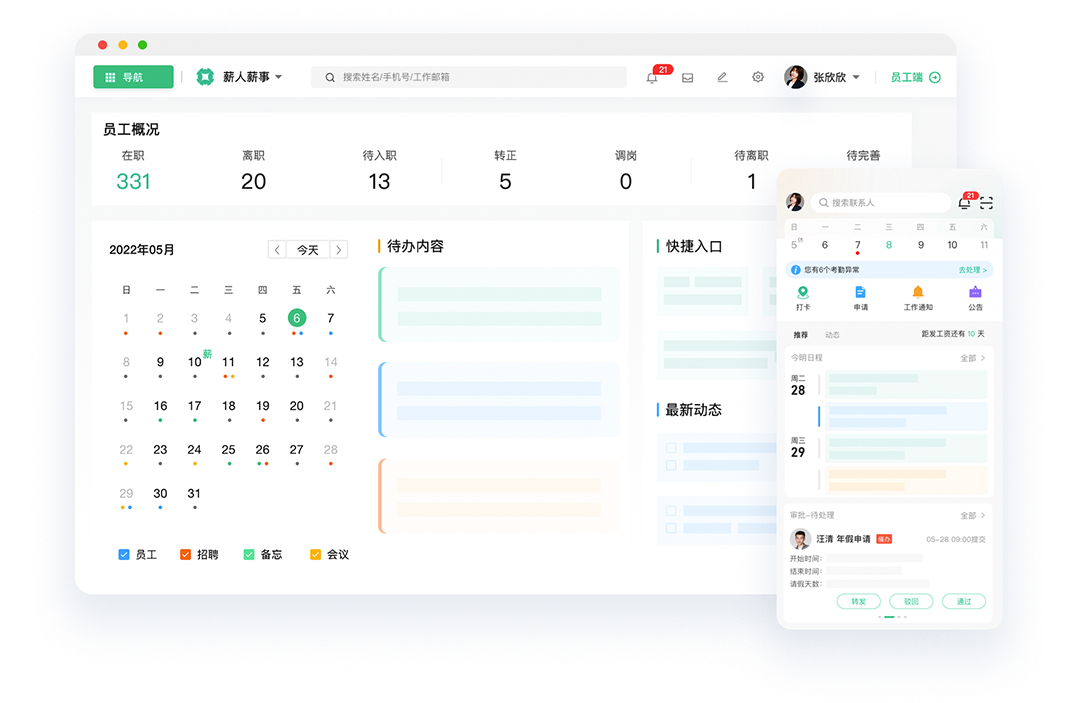
B端系统门门清之:HRM,人力资源系统,公司发展的源动力。
人才是公司发展的源动力,针对公司复杂人力的管理就是HRM系统的核心功能,本文就带领大家详细认识一下HRM系统,分别从什么是HRM系统,作用、功能模块、颜值提升四个方面来阐述。欢迎大家点赞评论收藏转发。 一、什么是HRM系统 HRM系…...

tplink安防监控raw文件转码合成mp4的方法
Tplink(深圳普联)专业的网络设备生产商,属于安防监控市场的后来者。Tplink的安防产品恢复了很多,其嵌入式文件系统也一直迭代更新。今天要说的案例比较特殊,其不仅仅要求恢复,还要求能解析出音频并且要求画面和声音实现“同步”。…...
- 聚类)
每天一个数据分析题(三百八十三)- 聚类
关于忽略自相关可以带来什么问题描述错误的是? A. 均方误差可能严重低估误差项的方差 B. 可能导致高估检验统计量t值,致使本不显著的变量变得显著了 C. 参数估计值的最小方差无偏性不再成立 D. 参数估计值的最小方差无偏性仍成立 数据分析认证考试介…...
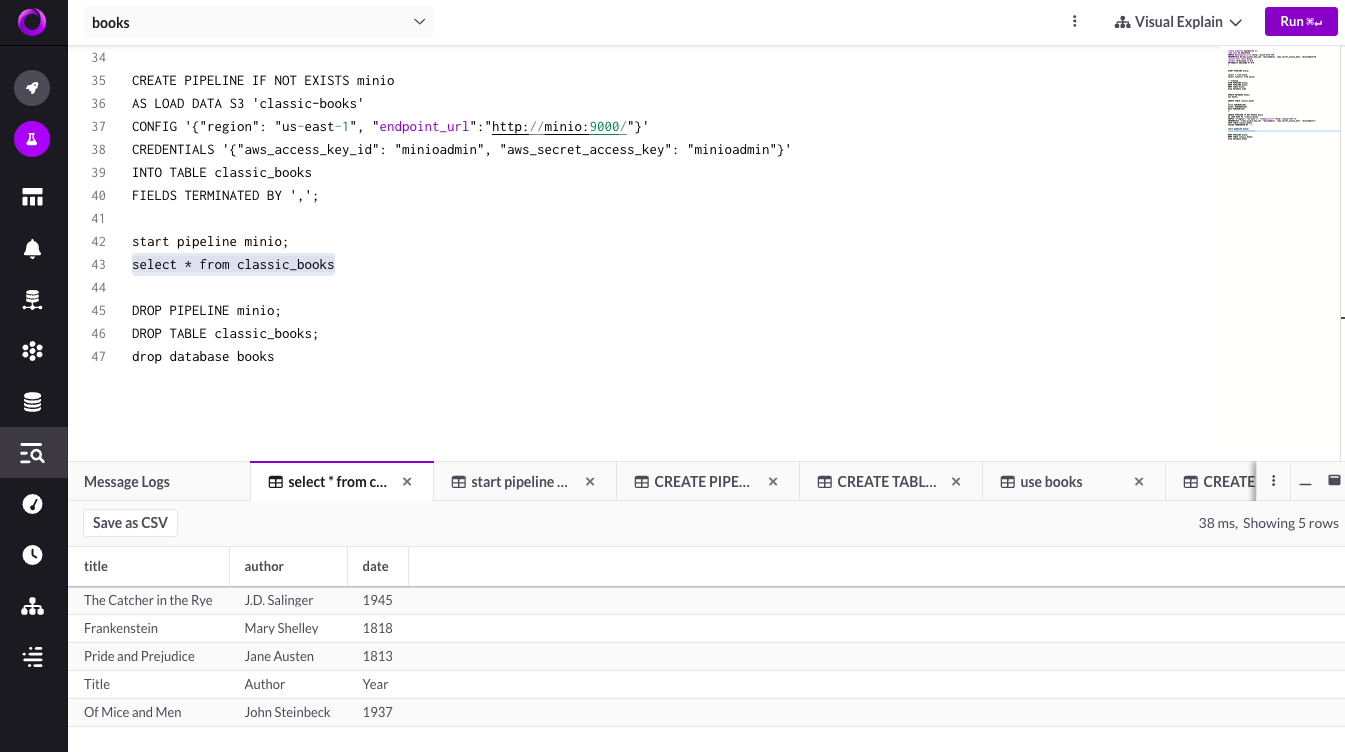
构建下一代数据解决方案:SingleStore、MinIO 和现代 Datalake 堆栈
SingleStore 是专为数据密集型工作负载而设计的云原生数据库。它是一个分布式关系 SQL 数据库管理系统,支持 ANSI SQL,并因其在数据引入、事务处理和查询处理方面的速度而受到认可。SingleStore 可以存储关系、JSON、图形和时间序列数据,以满…...

【经验分享】Ubuntu24.04安装微信
【经验分享】Ubuntu24.04安装微信(linux官方2024universal版) 文章如下,22.04和24.04微信兼容 【经验分享】Ubuntu22.04安装微信(linux官方2024universal版) 实测Ubuntu24.04LTS版本可以兼容。...
AXI学习笔记
文章目录 AXI口诀:AXI三种总线,三种接口,一个协议背景知识一、 AMBA:二、AXI2.1 通信协议与握手机制2.2 AXI协议特点2.3 三种AXI总线类型(AXI4、AXI4-lite、AXI4-stream)2.3.1 AXI通道(5通道&am…...

web vue 项目 Docker化部署
Web 项目 Docker 化部署详细教程 目录 Web 项目 Docker 化部署概述Dockerfile 详解 构建阶段生产阶段 构建和运行 Docker 镜像 1. Web 项目 Docker 化部署概述 Docker 化部署的主要步骤分为以下几个阶段: 构建阶段(Build Stage):…...

Cursor实现用excel数据填充word模版的方法
cursor主页:https://www.cursor.com/ 任务目标:把excel格式的数据里的单元格,按照某一个固定模版填充到word中 文章目录 注意事项逐步生成程序1. 确定格式2. 调试程序 注意事项 直接给一个excel文件和最终呈现的word文件的示例,…...

超短脉冲激光自聚焦效应
前言与目录 强激光引起自聚焦效应机理 超短脉冲激光在脆性材料内部加工时引起的自聚焦效应,这是一种非线性光学现象,主要涉及光学克尔效应和材料的非线性光学特性。 自聚焦效应可以产生局部的强光场,对材料产生非线性响应,可能…...

VB.net复制Ntag213卡写入UID
本示例使用的发卡器:https://item.taobao.com/item.htm?ftt&id615391857885 一、读取旧Ntag卡的UID和数据 Private Sub Button15_Click(sender As Object, e As EventArgs) Handles Button15.Click轻松读卡技术支持:网站:Dim i, j As IntegerDim cardidhex, …...

解锁数据库简洁之道:FastAPI与SQLModel实战指南
在构建现代Web应用程序时,与数据库的交互无疑是核心环节。虽然传统的数据库操作方式(如直接编写SQL语句与psycopg2交互)赋予了我们精细的控制权,但在面对日益复杂的业务逻辑和快速迭代的需求时,这种方式的开发效率和可…...

STM32F4基本定时器使用和原理详解
STM32F4基本定时器使用和原理详解 前言如何确定定时器挂载在哪条时钟线上配置及使用方法参数配置PrescalerCounter ModeCounter Periodauto-reload preloadTrigger Event Selection 中断配置生成的代码及使用方法初始化代码基本定时器触发DCA或者ADC的代码讲解中断代码定时启动…...

cf2117E
原题链接:https://codeforces.com/contest/2117/problem/E 题目背景: 给定两个数组a,b,可以执行多次以下操作:选择 i (1 < i < n - 1),并设置 或,也可以在执行上述操作前执行一次删除任意 和 。求…...

【2025年】解决Burpsuite抓不到https包的问题
环境:windows11 burpsuite:2025.5 在抓取https网站时,burpsuite抓取不到https数据包,只显示: 解决该问题只需如下三个步骤: 1、浏览器中访问 http://burp 2、下载 CA certificate 证书 3、在设置--隐私与安全--…...

Web 架构之 CDN 加速原理与落地实践
文章目录 一、思维导图二、正文内容(一)CDN 基础概念1. 定义2. 组成部分 (二)CDN 加速原理1. 请求路由2. 内容缓存3. 内容更新 (三)CDN 落地实践1. 选择 CDN 服务商2. 配置 CDN3. 集成到 Web 架构 …...

【Android】Android 开发 ADB 常用指令
查看当前连接的设备 adb devices 连接设备 adb connect 设备IP 断开已连接的设备 adb disconnect 设备IP 安装应用 adb install 安装包的路径 卸载应用 adb uninstall 应用包名 查看已安装的应用包名 adb shell pm list packages 查看已安装的第三方应用包名 adb shell pm list…...
