快速欧氏聚类与普通欧氏聚类比较
1、前言
文献《FEC: Fast Euclidean Clustering for Point Cloud Segmentation》介绍了一种快速欧氏聚类方法,大概原理可以参考如下图,具体原理可以参考参考文献。
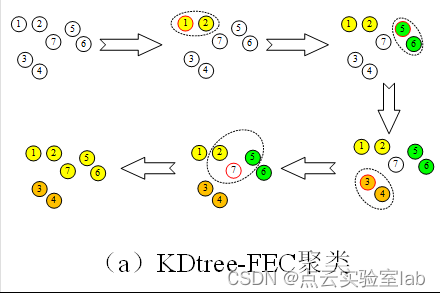
2、时间效率比较:快速欧氏聚类VS普通欧氏聚类
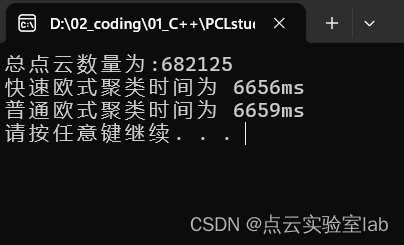
网上搜集的快速欧式聚类,与自己手写的普通欧式聚类进行对比,聚类结果相同。但是在算法效率上,两者相差很小。全部源代码如下,感兴趣的可以用自己数据进行测试。测试的点云数据量为68.2w个点,其中快速欧氏聚类耗时6656ms,普通欧氏聚类时间为6659ms。从下载的代码上来看,两者差别不大原因,可能是在寻找最小标号上,for循环上所占时间比较多。
#include<vector>
#include <pcl/point_types.h>
#include <pcl/point_cloud.h>
#include <pcl/kdtree/kdtree_flann.h>
#include<fstream>
#include<map>
#include<iomanip>
#include<time.h>
相关文章:

快速欧氏聚类与普通欧氏聚类比较
1、前言 文献《FEC: Fast Euclidean Clustering for Point Cloud Segmentation》介绍了一种快速欧氏聚类方法,大概原理可以参考如下图,具体原理可以参考参考文献。 2、时间效率比较:快速欧氏聚类VS普通欧氏聚类 网上搜集的快速欧式聚类,与自己手写的普通欧式聚类进行对比,…...

如何让大语言模型在规格普通的硬件上运行 - 量化技术
近年来,大型语言模型(LLMs)的能力有了飞跃式的发展,使其在越来越多的应用场景中更加友好和适用。然而,随着LLMs的智能和复杂度的增加,其参数数量,即权重和激活值的数量也在增加,这意…...

shell printf详解
默认的 printf 不会像 echo 自动添加换行符,我们可以手动添加 \n。 1. printf命令语法组成: printg format-string [arguments] 第一部分为格式化字符串,该字符串最好用引号括起来 第二部分为参数列表,例如字符串或变量值的列表,该列表需…...

【数据分析】用Python做事件抽取任务-快速上手方案
目录 方法一:使用OmniEvent库安装OmniEvent使用OmniEvent进行事件抽取OmniEvent优点缺点 方法二:使用大模型使用GPT网页版进行事件抽取事件类型列表 大模型优点缺点 总结 在自然语言处理(NLP)领域,事件抽取是一项关键任…...
B端系统门门清之:HRM,人力资源系统,公司发展的源动力。
人才是公司发展的源动力,针对公司复杂人力的管理就是HRM系统的核心功能,本文就带领大家详细认识一下HRM系统,分别从什么是HRM系统,作用、功能模块、颜值提升四个方面来阐述。欢迎大家点赞评论收藏转发。 一、什么是HRM系统 HRM系…...

tplink安防监控raw文件转码合成mp4的方法
Tplink(深圳普联)专业的网络设备生产商,属于安防监控市场的后来者。Tplink的安防产品恢复了很多,其嵌入式文件系统也一直迭代更新。今天要说的案例比较特殊,其不仅仅要求恢复,还要求能解析出音频并且要求画面和声音实现“同步”。…...
- 聚类)
每天一个数据分析题(三百八十三)- 聚类
关于忽略自相关可以带来什么问题描述错误的是? A. 均方误差可能严重低估误差项的方差 B. 可能导致高估检验统计量t值,致使本不显著的变量变得显著了 C. 参数估计值的最小方差无偏性不再成立 D. 参数估计值的最小方差无偏性仍成立 数据分析认证考试介…...
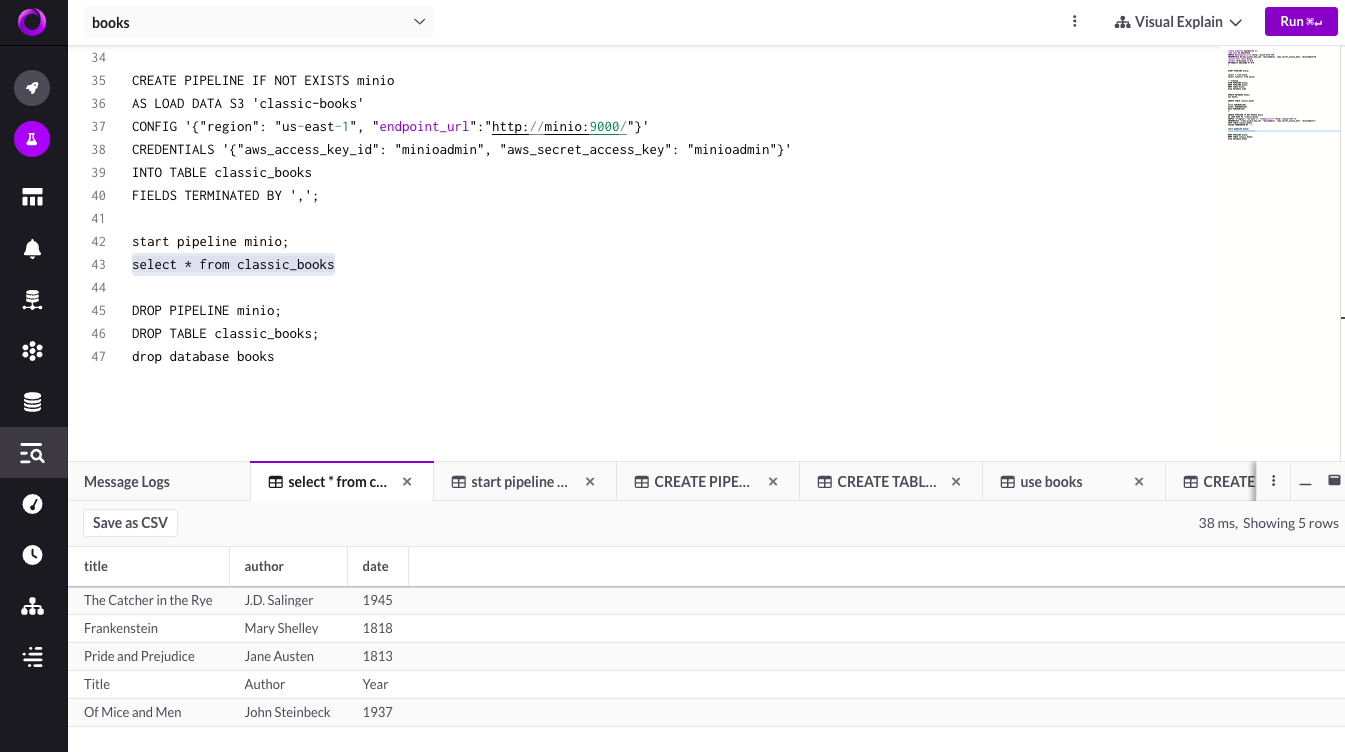
构建下一代数据解决方案:SingleStore、MinIO 和现代 Datalake 堆栈
SingleStore 是专为数据密集型工作负载而设计的云原生数据库。它是一个分布式关系 SQL 数据库管理系统,支持 ANSI SQL,并因其在数据引入、事务处理和查询处理方面的速度而受到认可。SingleStore 可以存储关系、JSON、图形和时间序列数据,以满…...

【经验分享】Ubuntu24.04安装微信
【经验分享】Ubuntu24.04安装微信(linux官方2024universal版) 文章如下,22.04和24.04微信兼容 【经验分享】Ubuntu22.04安装微信(linux官方2024universal版) 实测Ubuntu24.04LTS版本可以兼容。...
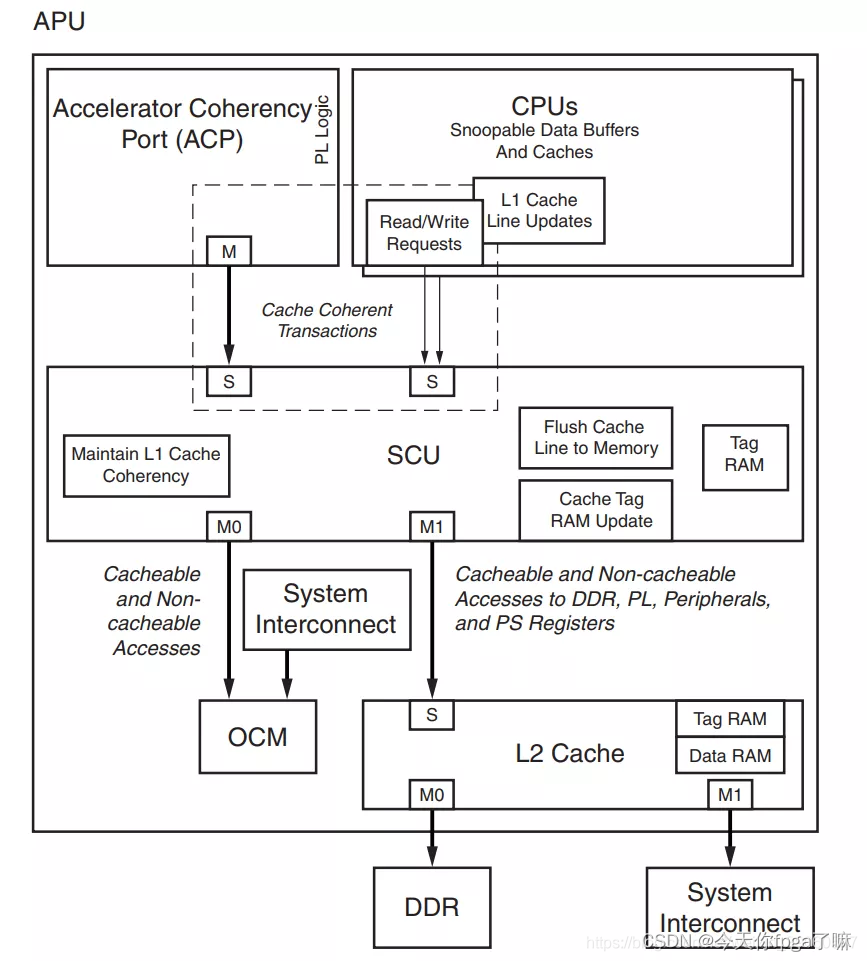
AXI学习笔记
文章目录 AXI口诀:AXI三种总线,三种接口,一个协议背景知识一、 AMBA:二、AXI2.1 通信协议与握手机制2.2 AXI协议特点2.3 三种AXI总线类型(AXI4、AXI4-lite、AXI4-stream)2.3.1 AXI通道(5通道&am…...
Spring boot 启动报:Do not use @ for indentation
一、使用maven插件动态切换配置时出现报错 二、配置文件及pom 2.1 配置文件结构 2.2 application.yml spring: # 根据环境读取配置文件(手动) # profiles: # active: dev# 根据环境读取配置文件(通过勾选maven插件)profiles…...

【数据结构】排序(下)
个人主页~ 排序(上) 栈和队列 排序 二、常见排序的实现8、快速排序的优化9、非递归快速排序(1)基本思想(2)代码实现(3)时间复杂度(4)空间复杂度 10、归并排序…...
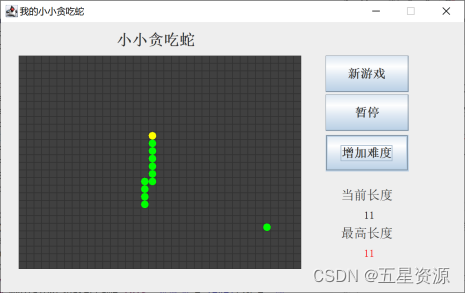
基于Java+Swing贪吃蛇小游戏(含课程报告)
博主介绍: 大家好,本人精通Java、Python、C#、C、C编程语言,同时也熟练掌握微信小程序、Php和Android等技术,能够为大家提供全方位的技术支持和交流。 我有丰富的成品Java、Python、C#毕设项目经验,能够为学生提供各类…...

三角形法恢复空间点深度
三角形法恢复空间点深度 如下图,以图 I 1 I_1 I1为参考,图 I 2 I_2 I2的变换矩阵为 T T T。相机光心为 O 1 O_1 O1和 O 2 O_2 O2。在图 I 1 I_1 I1中有特征点 p 1 p_1 p1,对应图 I 2 I_2 I2中有特征点 p 2 p_2 p2。理论上直…...

Linux 阻塞和非阻塞 IO 实验学习
Linux 阻塞和非阻塞 IO 实验学习 IO 指的是 Input/Output,也就是输入/输出,是应用程序对驱动设备的输入/输出操作。当应用程序对设备驱动进行操作的时候,如果不能获取到设备资源,那么阻塞式 IO 就会将应用程序对应的线程挂起&…...

JuiceFS 社区版 v1.2 发布,新增企业级权限管理、平滑升级功能
JuiceFS 社区版 v1.2 今天正式发布,这是自 2021 年开源以来的第三个大版本。v1.2 也是一个长期支持版本(LTS)。我们将持续维护 v1.2 以及 v1.1 这两个版本,v1.0 将停止更新。 JuiceFS 是为云环境设计的分布式文件系统,…...

虚拟3D沉浸式展会编辑平台降低了线上办展的门槛
在数字化浪潮的引领下,VR虚拟网上展会正逐渐成为企业展示品牌实力、吸引潜在客户的首选平台。我们与广交会携手走过三年多的时光,凭借优质的服务和丰富的经验,赢得了客户的广泛赞誉。 面对传统展会活动繁多、企业运营繁忙的挑战,许…...

泛微E9开发 查询页面添加按钮,完成特定功能
查询页面添加按钮,完成特定功能 1、关联知识(查询页面实现新增按钮)2、功能实现2.1. 点击按钮,输出选中的checkbox的值2.2. 点击按钮,打开一个自定义对话框 3、实现方法 1、关联知识(查询页面实现新增按钮&…...
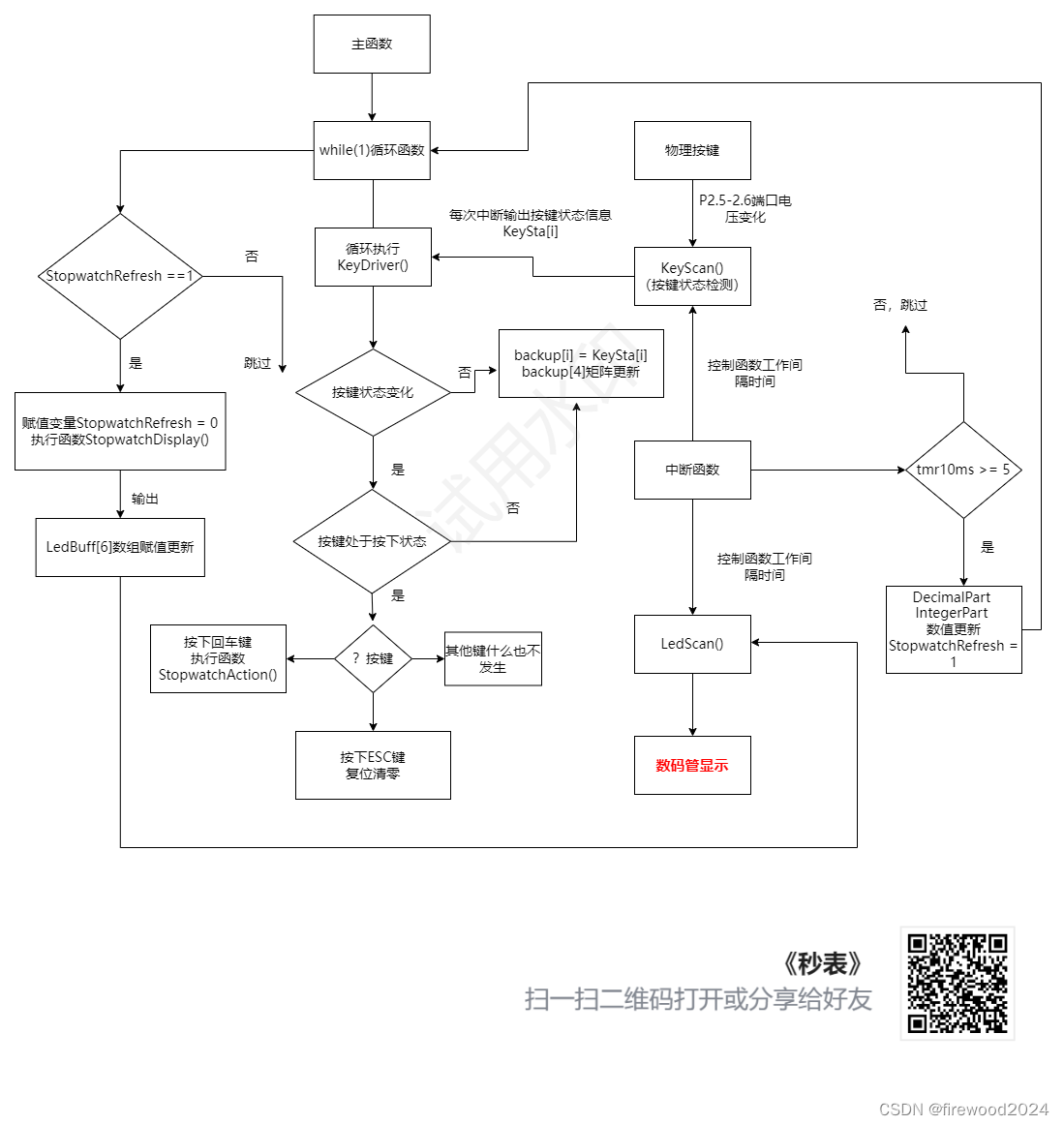
初学51单片机之数字秒表
不同数据类型间的相互转换 在C语言中,不同数据类型之间是可以混合运算的。当表达式中的数据类型不一致时,首先转换为同一类型,然后再进行计算。C语言有两种方式实现类型转换。一是自动类型转换,另外一种是强制类型转换。 转换的主…...
SpringBoot整合justauth实现多种方式的第三方登陆
目录 0.准备工作 1.引入依赖 2.yml文件 3. Controller代码 4.效果 参考 0.准备工作 你需要获取三方登陆的client-id和client-secret 以github为例 申请地址:Sign in to GitHub GitHub 1.引入依赖 <?xml version"1.0" encoding"UTF-8&quo…...

ES6从入门到精通:前言
ES6简介 ES6(ECMAScript 2015)是JavaScript语言的重大更新,引入了许多新特性,包括语法糖、新数据类型、模块化支持等,显著提升了开发效率和代码可维护性。 核心知识点概览 变量声明 let 和 const 取代 var…...

el-switch文字内置
el-switch文字内置 效果 vue <div style"color:#ffffff;font-size:14px;float:left;margin-bottom:5px;margin-right:5px;">自动加载</div> <el-switch v-model"value" active-color"#3E99FB" inactive-color"#DCDFE6"…...

tree 树组件大数据卡顿问题优化
问题背景 项目中有用到树组件用来做文件目录,但是由于这个树组件的节点越来越多,导致页面在滚动这个树组件的时候浏览器就很容易卡死。这种问题基本上都是因为dom节点太多,导致的浏览器卡顿,这里很明显就需要用到虚拟列表的技术&…...

MySQL用户和授权
开放MySQL白名单 可以通过iptables-save命令确认对应客户端ip是否可以访问MySQL服务: test: # iptables-save | grep 3306 -A mp_srv_whitelist -s 172.16.14.102/32 -p tcp -m tcp --dport 3306 -j ACCEPT -A mp_srv_whitelist -s 172.16.4.16/32 -p tcp -m tcp -…...

Maven 概述、安装、配置、仓库、私服详解
目录 1、Maven 概述 1.1 Maven 的定义 1.2 Maven 解决的问题 1.3 Maven 的核心特性与优势 2、Maven 安装 2.1 下载 Maven 2.2 安装配置 Maven 2.3 测试安装 2.4 修改 Maven 本地仓库的默认路径 3、Maven 配置 3.1 配置本地仓库 3.2 配置 JDK 3.3 IDEA 配置本地 Ma…...

【Go语言基础【12】】指针:声明、取地址、解引用
文章目录 零、概述:指针 vs. 引用(类比其他语言)一、指针基础概念二、指针声明与初始化三、指针操作符1. &:取地址(拿到内存地址)2. *:解引用(拿到值) 四、空指针&am…...

【笔记】WSL 中 Rust 安装与测试完整记录
#工作记录 WSL 中 Rust 安装与测试完整记录 1. 运行环境 系统:Ubuntu 24.04 LTS (WSL2)架构:x86_64 (GNU/Linux)Rust 版本:rustc 1.87.0 (2025-05-09)Cargo 版本:cargo 1.87.0 (2025-05-06) 2. 安装 Rust 2.1 使用 Rust 官方安…...

SQL慢可能是触发了ring buffer
简介 最近在进行 postgresql 性能排查的时候,发现 PG 在某一个时间并行执行的 SQL 变得特别慢。最后通过监控监观察到并行发起得时间 buffers_alloc 就急速上升,且低水位伴随在整个慢 SQL,一直是 buferIO 的等待事件,此时也没有其他会话的争抢。SQL 虽然不是高效 SQL ,但…...

AirSim/Cosys-AirSim 游戏开发(四)外部固定位置监控相机
这个博客介绍了如何通过 settings.json 文件添加一个无人机外的 固定位置监控相机,因为在使用过程中发现 Airsim 对外部监控相机的描述模糊,而 Cosys-Airsim 在官方文档中没有提供外部监控相机设置,最后在源码示例中找到了,所以感…...

淘宝扭蛋机小程序系统开发:打造互动性强的购物平台
淘宝扭蛋机小程序系统的开发,旨在打造一个互动性强的购物平台,让用户在购物的同时,能够享受到更多的乐趣和惊喜。 淘宝扭蛋机小程序系统拥有丰富的互动功能。用户可以通过虚拟摇杆操作扭蛋机,实现旋转、抽拉等动作,增…...
