探索C嘎嘎的奇妙世界:第十六关---STL(vector的练习)
1.只出现一次的数字

我们可以使用异或运算来解决这个问题:
异或运算有一个重要的性质:两个相同的数进行异或运算结果为 0,任何数与 0 异或结果为其本身。对于数组中的元素,依次进行异或运算,出现两次的元素异或后会变成 0,最后剩下的就是只出现一次的那个元素。
以下是具体步骤:
数组 [2,2,1],2^2=0,0^1=1,所以输出 1。
那么请看正确代码:
class Solution {
public:int singleNumber(vector<int>& nums) {int val=0;for(auto e :nums)val^=e;return val;}
};这是一种方法,然而还有一种传统的方法:
class Solution {
public:int singleNumber(vector<int>& nums) {int flag=0;for(size_t i=0;i<nums.size();i++){flag=0;for(size_t j=0;j<nums.size();j++){if(nums[i]==nums[j]&&i!=j)flag=1;}if(flag==0)return nums[i];}return 0;}
};上述代码首先创建一个变量flag并将其初始化为0,用于标记是否找到了只出现一次的元素。然后使用两个嵌套的循环遍历数组。外层循环用于遍历每个元素,内层循环用于比较当前元素与其他元素是否相等。如果找到了一个与当前元素相等且索引不同的元素,说明当前元素不是只出现一次的元素,将flag标记为1。最后,在外层循环中判断flag的值,如果flag为0,则说明当前元素是只出现一次的元素,直接返回该元素。如果循环结束后都没有找到只出现一次的元素,则返回0。
2.杨辉三角
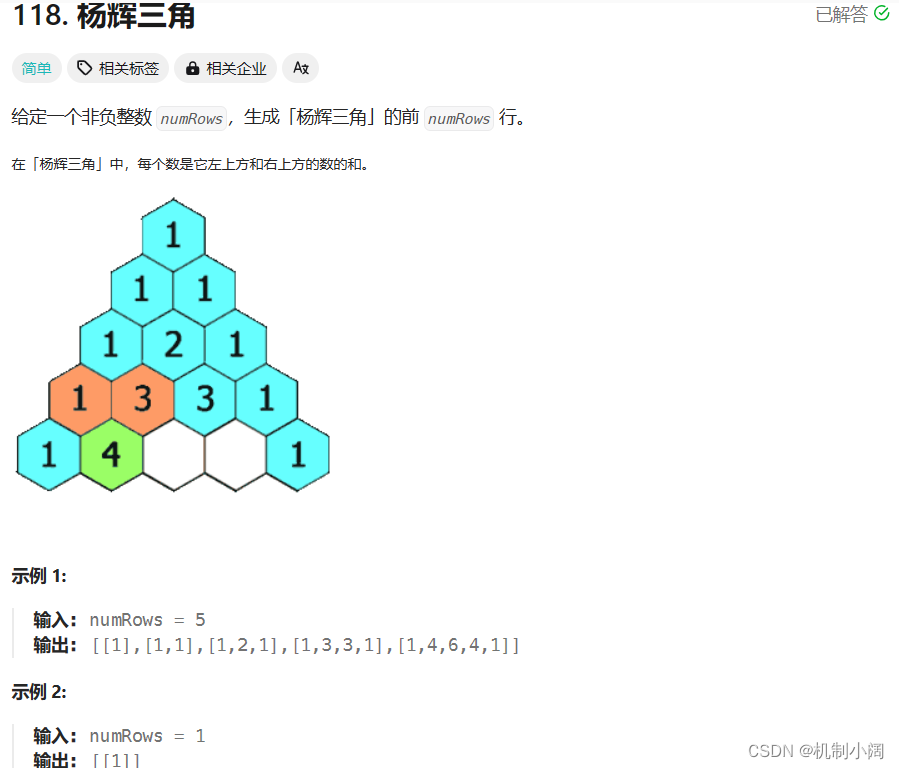
杨辉三角是一个数列,其第n行由 n个数字构成,每个数字等于它上方两个数字之和。首先,我们来看一下杨辉三角的定义:每一行的两侧数字都是1,中间的数字等于上一行对应位置的两个数字之和。可以使用二维数组来表示整个杨辉三角,其中第i行第j列的数字可以表示为triangle[i][j]。那么我们可以使用以下的编程思路来生成杨辉三角:
- 创建一个二维数组triangle,初始化为一个空的二维数组。
- 使用两个嵌套的循环来遍历杨辉三角的每一行和每一列,外层循环控制行数,内层循环控制列数。
- 在内层循环中,对于每一行的第一个位置和最后一个位置,将其值设置为1。
- 对于其他位置,将其值设置为其上一行对应位置的两个数字之和,即triangle[i][j] = triangle[i-1][j-1] + triangle[i-1][j]。
- 内层循环结束后,将当前行的数组添加到triangle中。
- 外层循环结束后,triangle中存储的就是完整的杨辉三角
请看正确代码:
class Solution {
public:vector<vector<int>> generate(int numRows) {vector<vector<int>> triangle;if (numRows <= 0) {return triangle;}for (int i = 0; i < numRows; i++) {vector<int> row(i+1, 1); // 初始化每一行为1for (int j = 1; j < i; j++) {row[j] = triangle[i-1][j-1] + triangle[i-1][j]; // 计算其他位置的值}triangle.push_back(row); // 将当前行添加到triangle中}return triangle;}
};这段代码使用了一个二维数组triangle来存储杨辉三角的每一行的数字。首先判断numRows的值,如果小于等于0,则直接返回空的triangle。然后,使用两个嵌套的循环来遍历杨辉三角的每一行和每一列。外层循环控制行数,内层循环控制列数。在内层循环中,对于每一行的第一个位置和最后一个位置,将其值设置为1。对于其他位置,将其值设置为其上一行对应位置的两个数字之和。内层循环结束后,将当前行的数组添加到triangle中。最后返回triangle即可得到完整的杨辉三角。这段代码的时间复杂度为O(numRows^2),其中numRows为所要生成杨辉三角的行数。因为需要使用两个嵌套的循环来遍历杨辉三角的每一行和每一列,时间复杂度较高。
3.删除有序数组中的重复项
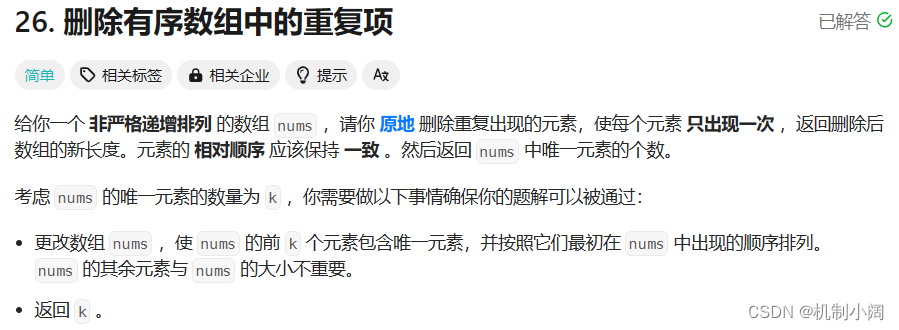

删除有序数组中的重复项可以使用双指针的方法来实现。具体的编程思路如下:
- 初始化两个指针:一个指针i用于遍历整个数组,另一个指针j用于指向当前确定的不重复元素的位置。
- 从数组的第二个元素开始遍历,即i=1。
- 如果当前元素nums[i]与前一个元素nums[i-1]相等,表示出现了重复元素,此时指针i继续向后移动一位。
- 如果当前元素nums[i]与前一个元素nums[i-1]不相等,表示找到了一个不重复的元素,将其复制到指针j的位置,并将指针j向后移动一位。
- 重复步骤3和步骤4,直到遍历完整个数组。
- 返回指针j的位置+1,即为删除重复项后的数组长度。
class Solution {
public:int removeDuplicates(vector<int>& nums) {if (nums.size() == 0) {return 0;}int j = 1; // 指针j初始指向第一个不重复元素的位置for (int i = 1; i < nums.size(); i++) {if (nums[i] != nums[i-1]) {nums[j++] = nums[i]; // 复制非重复元素到指针j的位置}}return j;}
};
这段代码使用了两个指针i和j。指针i用于遍历整个数组,指针j用于指向当前确定的不重复元素的位置。首先判断数组的长度是否为0,如果是则直接返回0。然后从数组的第二个元素开始遍历,即i=1。如果当前元素nums[i]与前一个元素nums[i-1]相等,表示出现了重复元素,此时指针i继续向后移动一位。如果当前元素nums[i]与前一个元素nums[i-1]不相等,表示找到了一个不重复的元素,将其复制到指针j的位置,并将指针j向后移动一位。重复上述步骤直到遍历完整个数组,最后返回指针j的位置+1,即为删除重复项后的数组长度。这段代码的时间复杂度为O(n),其中n为数组的长度。只需要遍历一次数组即可删除重复项,时间复杂度较低。
4.只出现一次的数字2.0

这道题和第一道题思路大概一致,只不过这里的重复次数变成了3次,还能不能使用异或呢,显然不能了,那我们第一道题的第二种方法能不能解呢?答案是可以的,那么请看示例代码:
class Solution {
public:int singleNumber(vector<int>& nums) {int flag=0;for(size_t i=0;i<nums.size();i++){flag=0;for(size_t j=0;j<nums.size();j++){if(nums[i]==nums[j]&&i!=j)flag=1;}if(flag==0)return nums[i];}return 0;}
};这里就不在解析了,思路和第一题的第二种方法一样。
5.只出现一次的数字3.0

思路依旧类似,只不过需要返回多个元素,只需要尾插到顺序表中即可,请看示例代码:
class Solution {
public:vector<int> singleNumber(vector<int>& nums) {vector<int> vv;int flag=0;for(size_t i=0;i<nums.size();i++){flag=0;for(size_t j=0;j<nums.size();j++){if(nums[i]==nums[j]&&i!=j)flag=1;}if(flag==0)vv.push_back(nums[i]);}return vv;}
};写法和前两种基本相似,不同之处在于,找到之后不会直接返回,而是尾插到顺序表中最后一块返回。
6.数组中出现次数超过一半的数字

常规写法就是统计他们出现的总次数,然后进行判断是否大于数组长度的一半,请看示例代码:
int count=0;for(size_t i=0;i<numbers.size();i++){count=1;for(size_t j=0;j<numbers.size();j++){if(numbers[i]==numbers[j]&&i!=j)count++; }if(count>numbers.size()/2)return numbers[i];}return 0;上述代码的具体的分析如下:
1. 初始化计数变量`count`为0。
2. 使用嵌套的循环结构遍历数组元素,外层循环是遍历数组中的每一个元素,内层循环是用来统计数组中该元素出现的次数。
3. 对于每一个外层循环迭代的元素,首先将计数变量`count`重置为1,表示当前元素至少出现了一次。
4. 然后通过内层循环遍历数组中的每一个元素,如果发现数组中有与当前元素相等的元素且索引不同,就将计数变量`count`加1。
5. 在内层循环结束后,判断计数变量`count`是否超过了数组长度的一半,如果超过了则说明该元素出现次数超过了数组长度的一半,直接返回该元素。
6. 如果没有找到出现次数超过数组长度一半的元素,最后返回0。
这段代码的时间复杂度为O(n^2),其中n为数组的长度。因为嵌套循环的复杂度为O(n^2),每个元素都需要遍历一次数组进行统计。所以在数组较大时,性能可能比较差。
那么有没有什么简单的方法呢?
分析一下题中的关键字“数组长度的一半“能不能想到把这个数组排序一下中间的就是我们要找的呢?哈哈,巧妙吧?那么请看示例代码吧:
class Solution {
public:int MoreThanHalfNum_Solution(vector<int>& numbers) {sort(numbers.begin(),numbers.end());return numbers[numbers.size()/2];}
};直接对数组进行排序,取其中间值就行。
到此我们只是简单的讲解了一下STL中vector的相关习题~,后续我们会一一展开学习的,希望这篇博客能给您带来一些启发和思考!那我们下次再一起探险喽,欢迎在评论区进行讨论~~~
相关文章:

探索C嘎嘎的奇妙世界:第十六关---STL(vector的练习)
1.只出现一次的数字 我们可以使用异或运算来解决这个问题: 异或运算有一个重要的性质:两个相同的数进行异或运算结果为 0,任何数与 0 异或结果为其本身。对于数组中的元素,依次进行异或运算,出现两次的元素异…...

最新扣子(Coze)实战案例:扣子卡片的制作及使用,完全免费教程
🧙♂️ 大家好,我是斜杠君,手把手教你搭建扣子AI应用。 📜 本教程是《AI应用开发系列教程之扣子(Coze)实战教程》,完全免费学习。 👀 关注斜杠君,可获取完整版教程。👍Ἷ…...

Node-red win11安装
文章目录 前言一、安装node.js和npm二、安装Node-red三、 运行Node-red 前言 Node-RED 是一种编程工具,用于以新颖有趣的方式将硬件设备、API 和在线服务连接在一起。 它提供了一个基于浏览器的编辑器,只需单击一下即可将调色板中的各种节点轻松连接在…...

永久更改R包的安装目录
要永久更改 R 包的安装目录,可以通过设置 R 配置文件来实现。以下是步骤说明: 1. 查找和修改 R 配置文件 R 有几个配置文件用于保存用户和系统的设置: 用户级配置文件:通常位于 ~/.Rprofile系统级配置文件:通常位于…...
)
Webrtc支持FFMPEG硬解码之NVIDA(二)
一、前言 此系列文章分分为三篇, Webrtc支持FFMPEG硬解码之Intel(一)-CSDN博客 Webrtc支持FFMPEG硬解码之NVIDA(二)-CSDN博客 Webrtc支持FFMPEG硬解码之解码实现-CSDN博客 AMD硬解目前还没找到可用解码器,欢迎留言交流 二、环境 Windows平台 VS2019 Cmake 三、下…...
)
整理好了!2024年最常见 20 道设计模式面试题(九)
上一篇地址:整理好了!2024年最常见 20 道设计模式面试题(八)-CSDN博客 十七、什么是享元模式?它在资源优化中扮演什么角色? 享元模式(Flyweight Pattern)是一种常用的软件设计模式…...

RAG实操教程langchain+Milvus向量数据库创建你的本地知识库 二
Miluvs 向量数据库 关于 Milvui 可以参考我的前两篇文章 • 一篇文章带你学会向量数据库Milvus(一)[1]• 一篇文章带你学会向量数据库Milvus(二)[2] 下面我们安装 pymilvus 库 pip install --upgrade --quiet pymilvus如果你…...
Spring+SpringMVC介绍+bean实例化+依赖注入实战
Spring介绍 Spring是一个轻量级的Java 开发框架,核心是IOC(控制反转)和AOP(面向切面编程) Spring解决了业务层(Service包)与其他各层(表现层,包括Model,Vie…...
【安装笔记-20240616-Linux-为 OpenWrt 自动挂载 Windows 主机共享目录】
安装笔记-系列文章目录 安装笔记-20240616-Linux-为 OpenWrt 自动挂载 Windows 主机共享目录 文章目录 安装笔记-系列文章目录安装笔记-20240616-Linux-为 OpenWrt 自动挂载 Windows 主机共享目录 前言一、软件介绍名称:cifsutils主页官方介绍特点 二、安装步骤测试…...

61.WEB渗透测试-信息收集- WAF、框架组件识别(1)
免责声明:内容仅供学习参考,请合法利用知识,禁止进行违法犯罪活动! 内容参考于: 易锦网校会员专享课 上一个内容:60.WEB渗透测试-信息收集- 端口、目录扫描、源码泄露(8) WAF的识…...

qmt量化交易策略小白学习笔记第45期【qmt编程之期货行情数据--如何获取日线行情、tick行情】
qmt编程之获取期货行情数据 qmt更加详细的教程方法,会持续慢慢梳理。 也可找寻博主的历史文章,搜索关键词查看解决方案 ! 感谢关注,咨询免费开通量化回测与获取实盘权限,欢迎和博主联系! 获取日线行情数…...

c#default 运算符
值类型默认值boolfalsebyte0char‘\0’decimal0.0Mdouble0.0Denum表达式 (E)0 产生的值,其中 E 为 enum 标识符。float0.0Fint0long0Lsbyte0short0struct将所有的值类型字段设置为默认值并将所有的引用类型字段设置为 null 时产生的值。uint0ulong0ushort0引用类型n…...

25计算机考研,这所985有机会!
吉林大学的计算机学科评估是A-,软件是B 实力还是很强的! 考研的专科课代码分别是941和966 其实就是自命题,941是四合一:数据结构,计算机组成与设计,操作系统和计算机网络,这个和408统考的科目…...

SQL 基础入门教程
目录 什么是 SQL? SQL 的基本操作 数据库的创建和删除 表的创建和删除 数据的插入 数据的查询 数据的更新 数据的删除 SQL 的高级操作 表的连接 聚合函数 分组和排序 子查询 视图 索引 SQL 的数据完整性和约束 总结 SQL(Structured Que…...

<Python><paddleocr>基于python使用百度paddleocr实现图片文字识别与替换
前言 本文是使用百度的开源库paddleocr来实现对图片文字的识别,准确度还不错,对图片文字的替换,则利用opencv来完成。 环境配置 系统:windows 平台:visual studio code 语言:python 库:paddleocr、opencv、pyqt5 依赖库安装 本例所需要的库可以直接用pip来安装。 安装…...

小程序开发的费用简介篇
小程序的价格跟很多因素有关系,比如你想要的复杂度、功能多不多等等 今天我就来具体说说开发一款APP/小程序到底需要多少 ❶功能复杂度:功能越多越复杂,开发时间和费用就越高,费用就会高 ❷设计要求:高级的…...

torch.unflod与torch.nn.functional.pad用法
PyTorch 中的两个函数:torch.unfold 和 torch.nn.unfold。它们分别用于不同的目的,让我们分别来理解一下: torch.nn.Unfold 类功能: 类似于函数 torch.unfold,torch.nn.Unfold 类也用于沿着指定维度滑动提取窗口并将每个窗口展平。与函数不同的是,torch.nn.Unfold 是一个…...

江苏 服务器性能监控包含哪些方面?
服务器的性能监控主要是为了确保服务器能够正常运行工作和性能优化的重要手段,接下来就来看一下服务器性能监控所包含的内容有哪些吧! 首先对于服务器的系统资源进行一定的监控,CPU作为服务器的核心组件之一,所以我们要监控CPU的使…...
卓越的 App UI 风格引领潮流
卓越的 App UI 风格引领潮流...
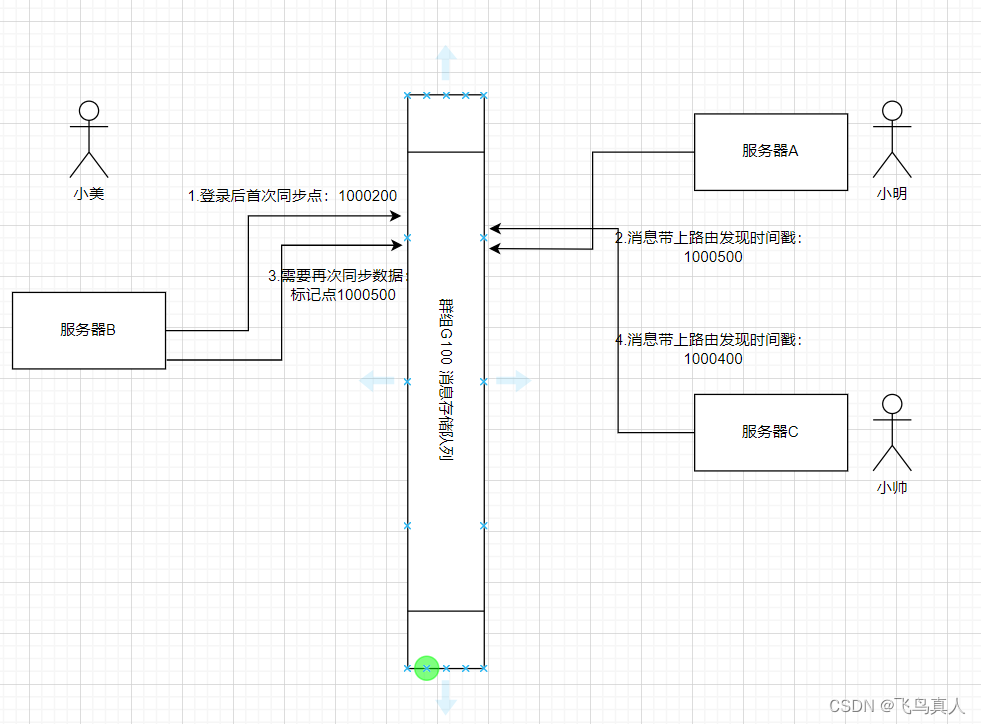
BirdTalk IM集群中消息流转策略讨论
BirdTalk IM集群中消息流转策略讨论 目前群聊的存储策略是1写多读方案;每个群组一个队列,按时间顺序排列,不区分用户; 私聊的存储是写扩散的,每个人都有自己的消息队列,按时间顺序 保存所有的消息&#x…...

Android Wi-Fi 连接失败日志分析
1. Android wifi 关键日志总结 (1) Wi-Fi 断开 (CTRL-EVENT-DISCONNECTED reason3) 日志相关部分: 06-05 10:48:40.987 943 943 I wpa_supplicant: wlan0: CTRL-EVENT-DISCONNECTED bssid44:9b:c1:57:a8:90 reason3 locally_generated1解析: CTR…...

Prompt Tuning、P-Tuning、Prefix Tuning的区别
一、Prompt Tuning、P-Tuning、Prefix Tuning的区别 1. Prompt Tuning(提示调优) 核心思想:固定预训练模型参数,仅学习额外的连续提示向量(通常是嵌入层的一部分)。实现方式:在输入文本前添加可训练的连续向量(软提示),模型只更新这些提示参数。优势:参数量少(仅提…...
)
Java 语言特性(面试系列1)
一、面向对象编程 1. 封装(Encapsulation) 定义:将数据(属性)和操作数据的方法绑定在一起,通过访问控制符(private、protected、public)隐藏内部实现细节。示例: public …...

遍历 Map 类型集合的方法汇总
1 方法一 先用方法 keySet() 获取集合中的所有键。再通过 gey(key) 方法用对应键获取值 import java.util.HashMap; import java.util.Set;public class Test {public static void main(String[] args) {HashMap hashMap new HashMap();hashMap.put("语文",99);has…...

使用分级同态加密防御梯度泄漏
抽象 联邦学习 (FL) 支持跨分布式客户端进行协作模型训练,而无需共享原始数据,这使其成为在互联和自动驾驶汽车 (CAV) 等领域保护隐私的机器学习的一种很有前途的方法。然而,最近的研究表明&…...

基础测试工具使用经验
背景 vtune,perf, nsight system等基础测试工具,都是用过的,但是没有记录,都逐渐忘了。所以写这篇博客总结记录一下,只要以后发现新的用法,就记得来编辑补充一下 perf 比较基础的用法: 先改这…...

linux 下常用变更-8
1、删除普通用户 查询用户初始UID和GIDls -l /home/ ###家目录中查看UID cat /etc/group ###此文件查看GID删除用户1.编辑文件 /etc/passwd 找到对应的行,YW343:x:0:0::/home/YW343:/bin/bash 2.将标红的位置修改为用户对应初始UID和GID: YW3…...

k8s业务程序联调工具-KtConnect
概述 原理 工具作用是建立了一个从本地到集群的单向VPN,根据VPN原理,打通两个内网必然需要借助一个公共中继节点,ktconnect工具巧妙的利用k8s原生的portforward能力,简化了建立连接的过程,apiserver间接起到了中继节…...

【Oracle】分区表
个人主页:Guiat 归属专栏:Oracle 文章目录 1. 分区表基础概述1.1 分区表的概念与优势1.2 分区类型概览1.3 分区表的工作原理 2. 范围分区 (RANGE Partitioning)2.1 基础范围分区2.1.1 按日期范围分区2.1.2 按数值范围分区 2.2 间隔分区 (INTERVAL Partit…...

DeepSeek 技术赋能无人农场协同作业:用 AI 重构农田管理 “神经网”
目录 一、引言二、DeepSeek 技术大揭秘2.1 核心架构解析2.2 关键技术剖析 三、智能农业无人农场协同作业现状3.1 发展现状概述3.2 协同作业模式介绍 四、DeepSeek 的 “农场奇妙游”4.1 数据处理与分析4.2 作物生长监测与预测4.3 病虫害防治4.4 农机协同作业调度 五、实际案例大…...
