【考研408计算机组成原理】数值表示和运算之快速数值转换

苏泽
“弃工从研”的路上很孤独,于是我记下了些许笔记相伴,希望能够帮助到大家
另外,利用了工作之余的一点点时间,整理了一套考研408的知识图谱,
我根据这一套知识图谱打造了这样一个408知识图谱问答系统
里面的每一个回答都是根据考研408的考点回复的

目前暂时只接入了微信,如果大家对这个问答系统感兴趣的话可以在我的主页里找到我的微信号
找我拉进测试群免费体验哦
这一章希望分享一份快速数值转换的技巧笔记
目录
这一章希望分享一份快速数值转换的技巧笔记
数值转换的几个方向
进制转换
这里我们可以观察这个表发现一个规律,那就是所有十六进制的每一位都能够用 二进制的四位来表示
各种“码”的转换
关于原码、反码、补码以及移码的转换,以下是整理的要点:
其中原码转补码的小技巧
考研易错点难点:浮点数
先说浮点数的定义
☆求补运算的使用
数值转换的几个方向
进制转换
首先考研只会考到2进制 10进制 和16进制的转换 所以对于这些数值之间的表示和不同进制之间的转换就成为了一项必备技能
而这些进制的转换相信大家都不陌生 通过辗转相除法之类的计算方法就能计算得出, 但我这里要记录的 是一种能够通过少量记忆 达到免除计算 节省时间的一种方法
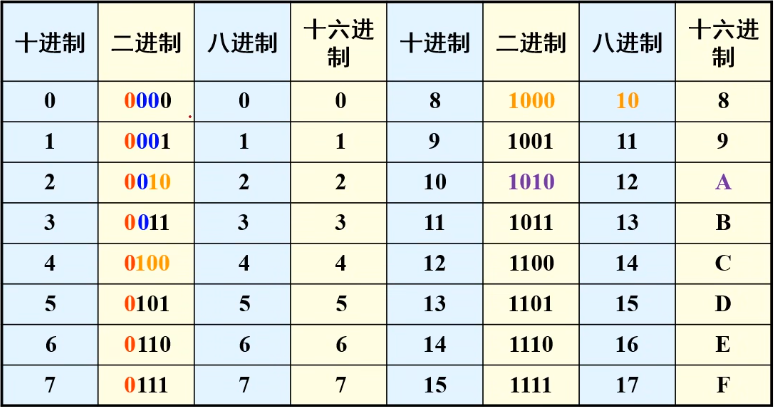
首先我们可以看到这样一个表 这个表并不稀奇 大家也能自己去算一下 也不需要背考试的时候
其实只需要把16进制当中的A~F对应的十进制数给写到草稿纸上即可
A~F分别对应的是10~15
这里我们可以观察这个表发现一个规律,那就是所有十六进制的每一位都能够用 二进制的四位来表示
用下面这个例子快速掌握这个小技巧

这里要求16进制转2进制
那么现在问题就变成了“3”如何用4位二进制表示,是不是2的1次方+2的0次方,所以是0011
B是11 =8+0+2+1 所以是1011
...以此类推
这样我们把每一位转成二进制的数 都写到纸上 然后按顺序拼起来就是结果了
就不需要用传统方法模16那种方法 无需计算快速得出结果
各种“码”的转换
再到经典的原、反、补、移码了
先看这张整理好的图
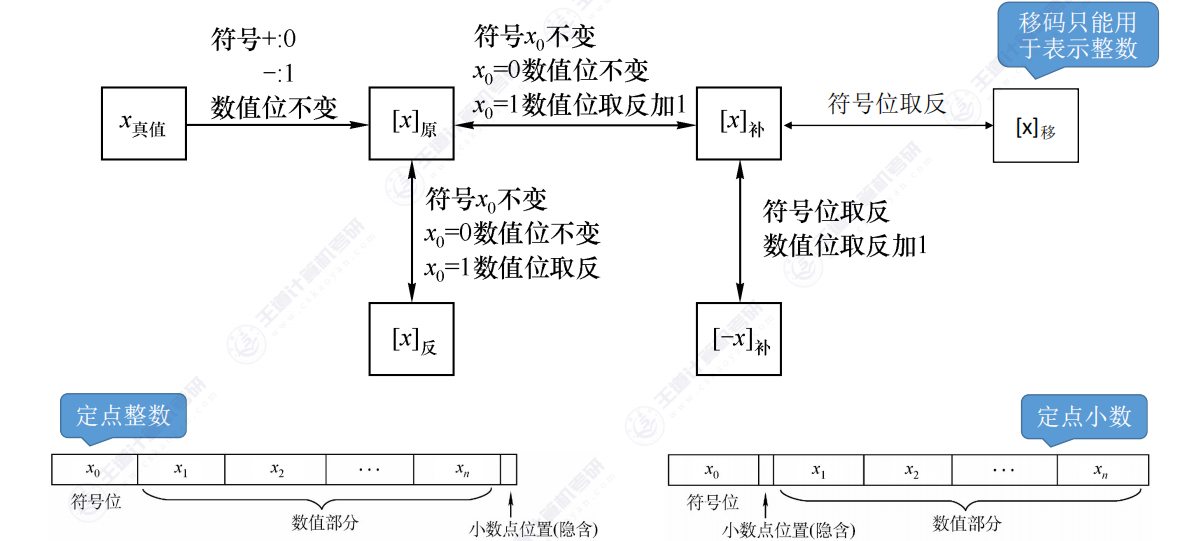
关于原码、反码、补码以及移码的转换,以下是整理的要点:
-
原码:
- 原码是最直接的表示方式,最高位是符号位,0代表正数,1代表负数。其余位表示数值的大小。
-
反码:
- 正数的反码与其原码相同。
- 负数的反码是将其原码除符号位外的所有位取反。
-
补码:
- 正数的补码与其原码相同。
- 负数的补码是其反码加1。
-
移码:
- 移码是补码的一种变体,其符号位取反。这使得正数的移码比补码大1,而负数的移码比补码小1。
其中原码转补码的小技巧
这里有个小技巧 王道里面也说过的:符号位不变,从左往右数第一个“1” ,它的左边全取反 右边保留原样
这个技巧能够其他转换当中的完美等价“数值位取反加1”这一条件
考研易错点难点:浮点数
先说浮点数的定义
之所以“浮” 是因为他的小数点 飘忽不定 例如1.01 可以写成10.1*10^-1
所以计算机当中需要一个统一的标准 将这些小数给统一起来 就有了下面的部分 来介绍计算机是如何统一的表示浮点数的
-
浮点数的组成:
- 浮点数通常由三部分组成:阶码(Exponent)、尾数(Mantissa)和符号位(Sign)。

关于浮点数移位的解释 和记忆的口诀
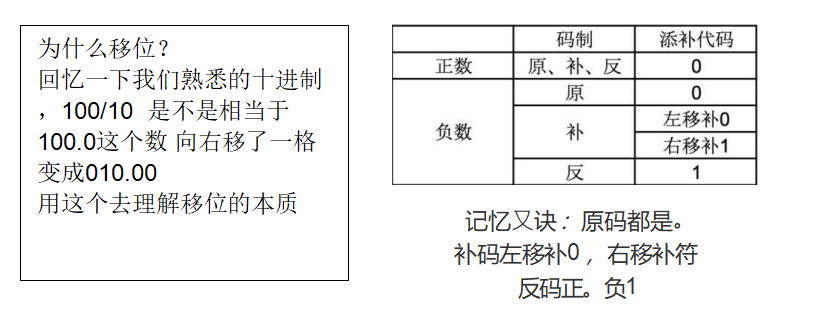
逻辑移位: 将操作数视为⽆符号 ,⼀律补0
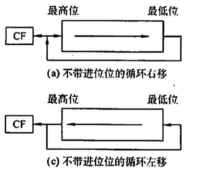
循环移位: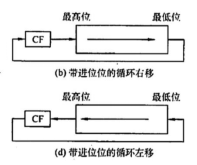
☆求补运算的使用
负16进制->补码 (快速)
原码
正数补码=原码,所以不多说
负数2进制补码: ⽤常归⽅法即可
负数16进制补码: 求补运算,说⽩了就是求这个数的⼀个互补值,使得这个数最高位能够进1位且其他位都为 0,这种运算就称之为“求补运算 ”
例 :求带符 号补 码FCA358H的 真值?
使用求补运算相当求让FCA358H加上一个数使其=10000000H
FCA358H+035CA8H= 10000000H
此时我们求出来的是FCA358H的补数,由于FCA358H显然是负数, 所以在转为真值的时候 一 定要记得加上负号! !
同时,将有符号补数转为原码时也要保持符号一致性,所以最后FCA358H的原码为: 835CA8H
1000H-002BH =FFD5H
相关文章:

【考研408计算机组成原理】数值表示和运算之快速数值转换
苏泽 “弃工从研”的路上很孤独,于是我记下了些许笔记相伴,希望能够帮助到大家 另外,利用了工作之余的一点点时间,整理了一套考研408的知识图谱, 我根据这一套知识图谱打造了这样一个408知识图谱问答系统 里面的每一…...

理解 JTBD 框架和EJ 理念:深挖以用户为中心的设计
在与用户的交流中,我们发现对用户需求的精准洞察普遍困扰着产品经理、设计、企划人员,因为当今消费者行为已经由单品消费转向场景消费,千人千面的个性化需求出现,消费者数据维度极大丰富,这对把握用户体验造成了很大挑…...

数据提取与治理:企业实现数据驱动决策的必经之路
数据提取与治理:企业实现数据驱动决策的必经之路 随着信息技术的迅猛发展,数据已经成为企业最宝贵的资产之一。然而,数据并非天生就具有价值,只有通过有效的提取和治理,才能转化为企业决策的有力支撑。本文将探讨数据…...
Avalonia:一个.NET跨平台UI框架
概述 Avalonia是一个强大的框架,使开发人员能够使用. NET创建跨平台应用程序。它使用自己的渲染引擎来绘制UI控件,确保在各种平台上保持一致的外观和行为,包括Windows,macOS,Linux,Android,iOS…...
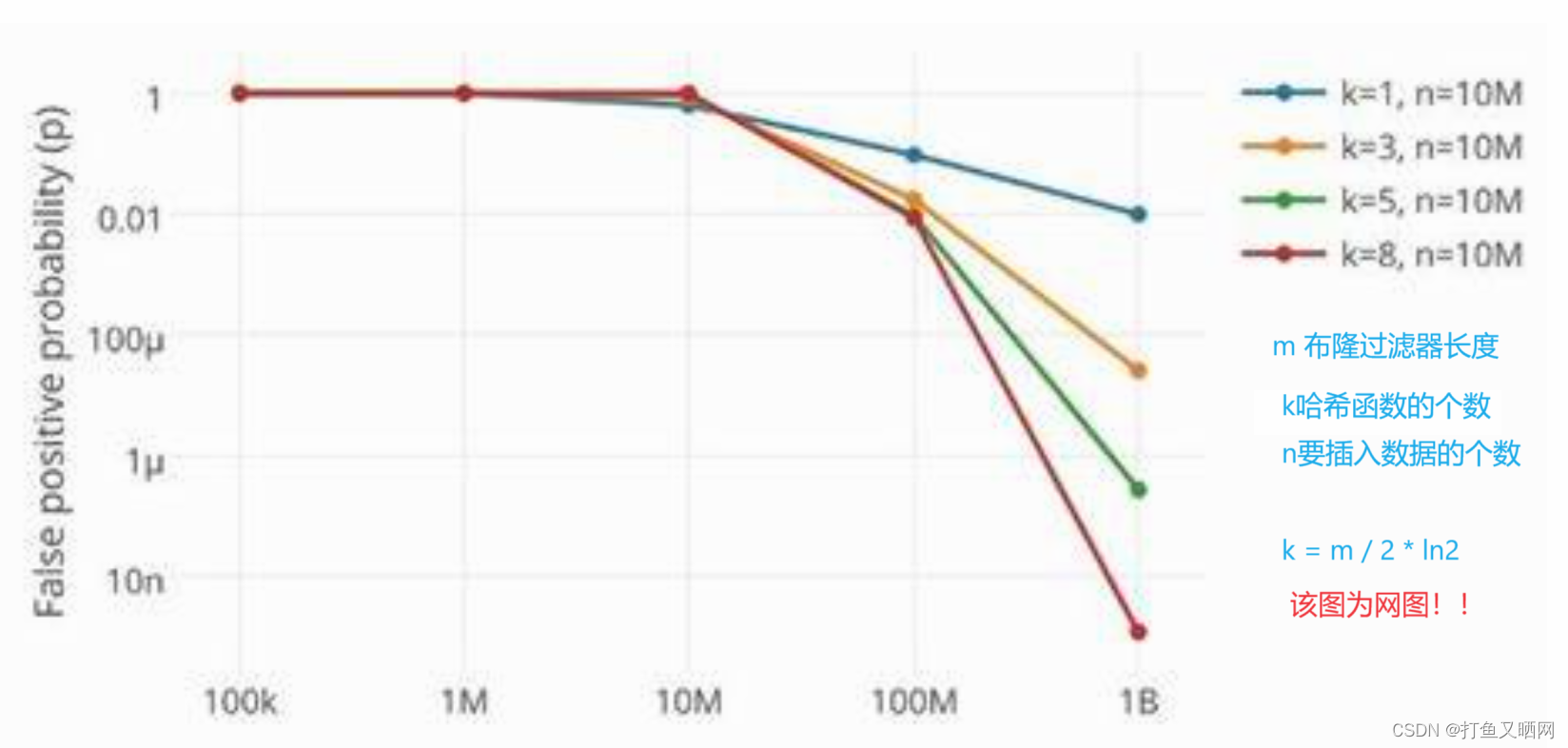
海量数据处理——bitMap/BloomFilter、hash + 统计 + 堆/归并/快排
前言:海量数据处理是面试中一道常考的问题, 生活中也容易遇到这种问题。 通常就是有一个大文件, 让我们对这个文件进行一系列操作——找出现次数最多的数据、求交集、是否重复出现等等。 因为文件的内容太多, 我们的内存通常是放不…...
)
TrainingArguments、ModelArguments、DataArguments参数使用(@dataclass)
文章目录 前言一、@dataclass装饰器说明二、transformers.HfArgumentParser参数使用Demo三、field函数四、llava模型参数1、模型参数设置2、数据参数设置3、训练参数设置4、参数解析5、参数传递6、参数添加前言 理解llava相关参数传递方法,有利于我们对模型修改模块使用参数来…...
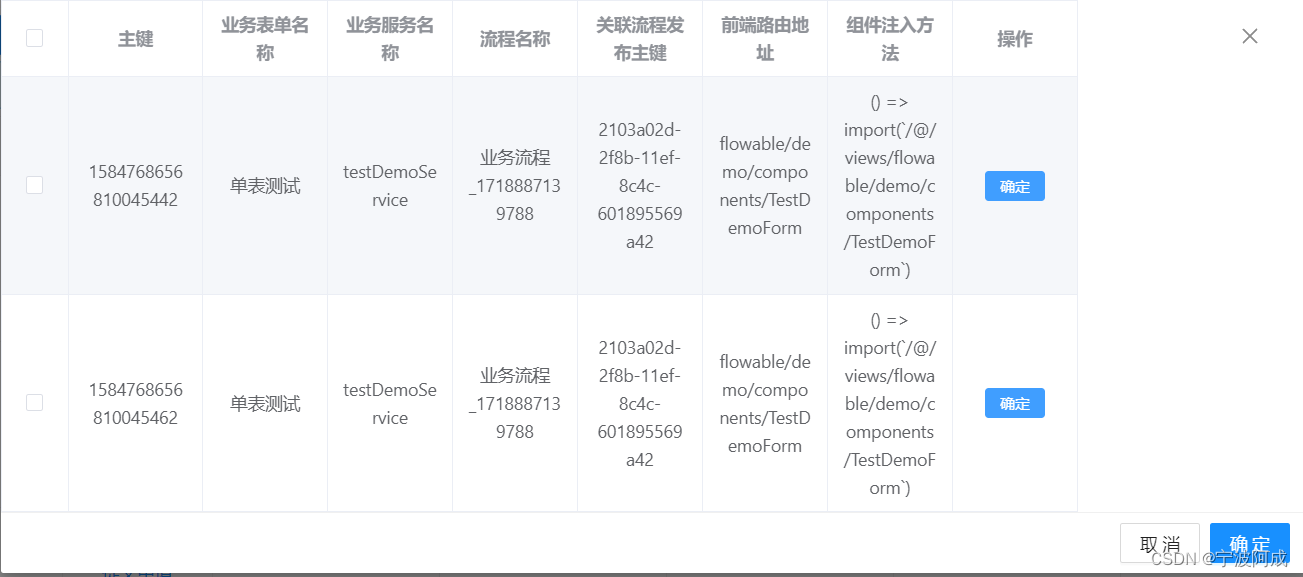
基于jeecgboot-vue3的Flowable流程-自定义业务表单处理(一)支持同一个业务多个关联流程的选择支持
因为这个项目license问题无法开源,更多技术支持与服务请加入我的知识星球。 这部分先讲讲支持自定义业务表单一个业务服务表单多个流程的支持处理 1、后端mapper部分 如下,修改selectSysCustomFormByServiceName为list对象,以便支持多个 &…...
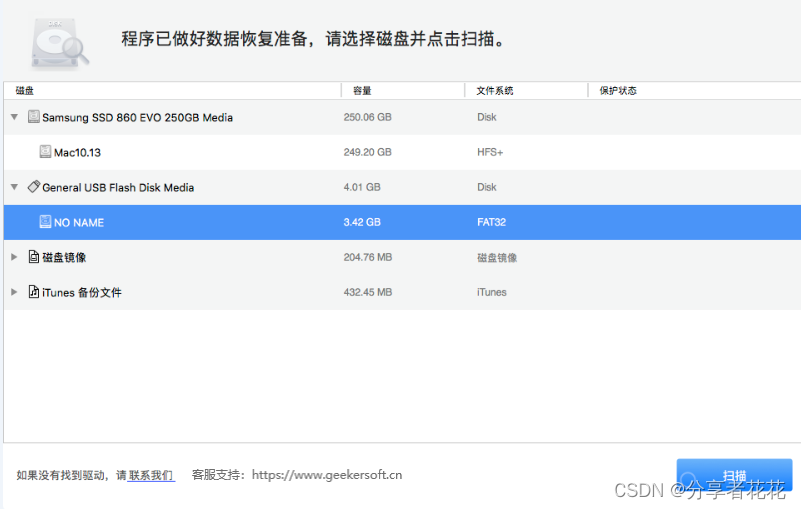
解决数据丢失问题的MacOS 数据恢复方法
每个人都经历过 Mac 硬盘或 USB 驱动器、数码相机、SD/存储卡等数据丢失的情况。我们中的一些人可能认为已删除或格式化的数据将永远丢失,因此就此作罢。对于 macOS 用户来说,当文件被删除时,垃圾箱已被清空,他们可能不知道如何恢…...

[ARM-2D 专题]3. ##运算符
C语言的宏系统相当强大,它允许使用##符号来处理预处理期的文本替换。这种用法被称为标记连接(token pasting)操作,其结果是将两个标记紧紧地连接在一起,而省略掉它们之间的所有空格。在复杂的宏定义中,运用…...
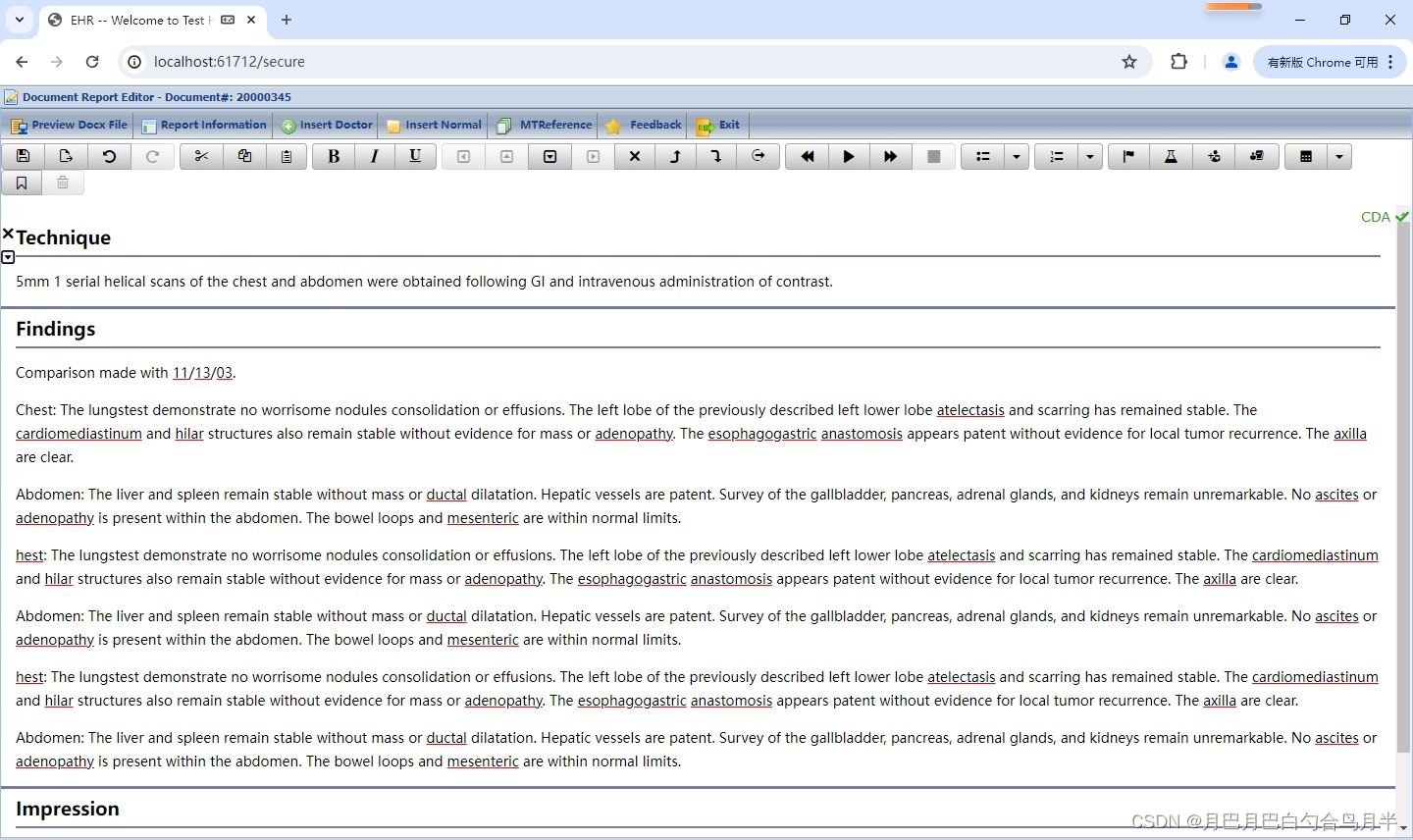
基于语音识别的智能电子病历(五)电子病历编辑器
前言 首先我们要明确一个概念:很多电子病历的编辑器,在输入文字的地方,有个麦克风按钮,点击一下,可以进行录音,然后识别的文字会自动输入到电子病历中,这种方式其实不能称为“基于语音识别的智…...
云计算技术高速发展,优势凸显
云计算是一种分布式计算技术,其特点是通过网络“云”将巨大的数据计算处理程序分解成无数个小程序,并通过多部服务器组成的系统进行处理和分析这些小程序,最后将结果返回给用户。它融合了分布式计算、效用计算、负载均衡、并行计算、网络存储…...
文本三剑客其二
文本三剑客其二 sed和awk grep就是查找文本当中的内容,扩展正则表达式。 sed 对文本内容进行增删改查 sed是一种流编辑器,一次处理一行内容。 如果只是展示,会放在缓冲区(模式空间),展示结束之后&…...

【达梦数据库】typeorm+node.js+达梦数据库返回自增列值
1.配置环境,下载依赖包 typeorm init --name test22 --database mysql typeorm-dm,uuid,typeorm2,修改连接信息 修改src/ data-source.ts 文件 连接dm,可参考刚刚安装typeorm-dm 模块中的 README.md 3.修改自增信息 /* 修改前*/PrimaryGen…...

【ARMv8/ARMv9 硬件加速系列 2.1 -- ARM NEON 向量寄存器单个元素赋值】
文章目录 NEON 向量寄存器单个元素赋值对 v0.4s中的一个元素赋值对 v1.16b 中的一个元素赋值MOVI (Move Immediate)NEON 向量寄存器单个元素赋值 在ARMv8架构中,你可以使用特定的指令来对v0.4s和v1.16b中的单个元素赋值。这通常通过使用MOV(Move)指令的变种实现,具体取决于…...
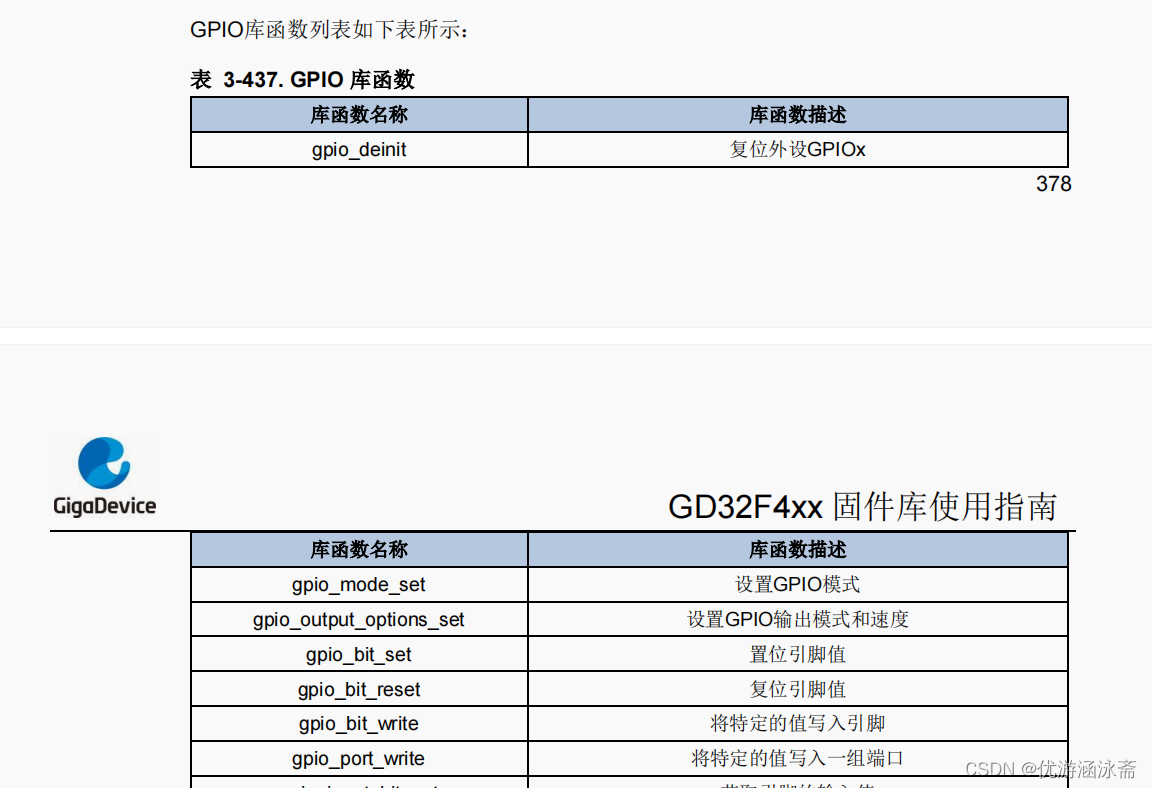
GD32学习
参考视频13.立创开发板GD32教程:串口配置_哔哩哔哩_bilibili 固件库跟用户手册基本上差不多,只不过用用户手册编写程序的话会更加的底层,固件库的话就是把一些函数封装起来,用的时候拿过来即可,目前我还没有找到固件库…...
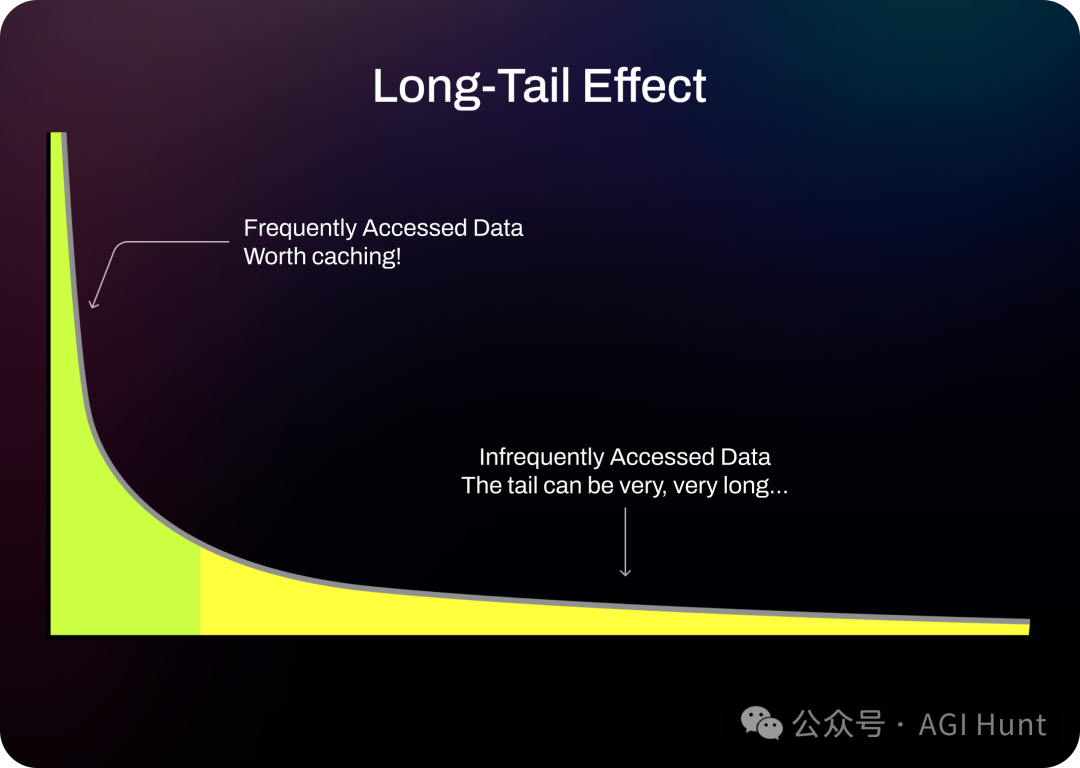
LangChain:如何高效管理 LLM 聊天历史记录?
LangChain 团队发布了一篇关于使用 Dragonfly DB 来有效管理 LangChain 应用程序聊天历史记录的教程。 该教程旨在解决用户在使用 LangChain 应用程序时普遍遇到的一个问题:如何高效地管理聊天历史记录。 LangChain 团队在推文中强调了 Dragonfly DB 在管理聊天历…...

【React】useState 更新延迟的原因是什么,怎么解决?
useState 更新延迟的原因 异步更新:React 中的 useState 更新是异步的,这意味着当你调用更新函数(如 setData)时,React 并不立即同步更新状态,而是将其放入一个待处理的队列中,稍后在适当的时候(如在下一次渲染之前)进行处理。因此,如果你尝试在调用更新函数后立即读…...

非关系型数据库NoSQL数据层解决方案 之 redis springboot整合与读写操作 2024详解以及window版redis5.0.14下载百度网盘
redis下载安装以及基本使用 下载地址 链接:百度网盘 请输入提取码 提取码:0410 一个名对应一个数值 内存级 在内存里进行操作 准备启动 我们现在就有一个redis客户端的服务器了 我们再启动一个cmd 操作redis数据库 redis里面的基本数据类型有五种 …...

jigdo无法下载的文件
问题描述 用jigdo下载Debian的iso镜像,剩下最后一个文件下载不了,提示信息: Found 0 of the 1 files required by the template Copied input files to temporary file debian-12.5.0-amd64-DLBD-2.iso.tmp - repeat command and supply mo…...

C#面:C# 类的执行顺序?
C# 类的执行顺序可以分为以下几个步骤: 静态字段初始化:在类的第一次使用之前,静态字段会被初始化。静态字段的初始化顺序是按照它们在代码中的声明顺序进行的。静态构造函数:如果类中定义了静态构造函数,它会在类的第…...

【Java学习笔记】Arrays类
Arrays 类 1. 导入包:import java.util.Arrays 2. 常用方法一览表 方法描述Arrays.toString()返回数组的字符串形式Arrays.sort()排序(自然排序和定制排序)Arrays.binarySearch()通过二分搜索法进行查找(前提:数组是…...

关于iview组件中使用 table , 绑定序号分页后序号从1开始的解决方案
问题描述:iview使用table 中type: "index",分页之后 ,索引还是从1开始,试过绑定后台返回数据的id, 这种方法可行,就是后台返回数据的每个页面id都不完全是按照从1开始的升序,因此百度了下,找到了…...

论文浅尝 | 基于判别指令微调生成式大语言模型的知识图谱补全方法(ISWC2024)
笔记整理:刘治强,浙江大学硕士生,研究方向为知识图谱表示学习,大语言模型 论文链接:http://arxiv.org/abs/2407.16127 发表会议:ISWC 2024 1. 动机 传统的知识图谱补全(KGC)模型通过…...

Android 之 kotlin 语言学习笔记三(Kotlin-Java 互操作)
参考官方文档:https://developer.android.google.cn/kotlin/interop?hlzh-cn 一、Java(供 Kotlin 使用) 1、不得使用硬关键字 不要使用 Kotlin 的任何硬关键字作为方法的名称 或字段。允许使用 Kotlin 的软关键字、修饰符关键字和特殊标识…...

Caliper 配置文件解析:fisco-bcos.json
config.yaml 文件 config.yaml 是 Caliper 的主配置文件,通常包含以下内容: test:name: fisco-bcos-test # 测试名称description: Performance test of FISCO-BCOS # 测试描述workers:type: local # 工作进程类型number: 5 # 工作进程数量monitor:type: - docker- pro…...

基于PHP的连锁酒店管理系统
有需要请加文章底部Q哦 可远程调试 基于PHP的连锁酒店管理系统 一 介绍 连锁酒店管理系统基于原生PHP开发,数据库mysql,前端bootstrap。系统角色分为用户和管理员。 技术栈 phpmysqlbootstrapphpstudyvscode 二 功能 用户 1 注册/登录/注销 2 个人中…...

Vite中定义@软链接
在webpack中可以直接通过符号表示src路径,但是vite中默认不可以。 如何实现: vite中提供了resolve.alias:通过别名在指向一个具体的路径 在vite.config.js中 import { join } from pathexport default defineConfig({plugins: [vue()],//…...

Python训练营-Day26-函数专题1:函数定义与参数
题目1:计算圆的面积 任务: 编写一个名为 calculate_circle_area 的函数,该函数接收圆的半径 radius 作为参数,并返回圆的面积。圆的面积 π * radius (可以使用 math.pi 作为 π 的值)要求:函数接收一个位置参数 radi…...

加密通信 + 行为分析:运营商行业安全防御体系重构
在数字经济蓬勃发展的时代,运营商作为信息通信网络的核心枢纽,承载着海量用户数据与关键业务传输,其安全防御体系的可靠性直接关乎国家安全、社会稳定与企业发展。随着网络攻击手段的不断升级,传统安全防护体系逐渐暴露出局限性&a…...

基于单片机的宠物屋智能系统设计与实现(论文+源码)
本设计基于单片机的宠物屋智能系统核心是实现对宠物生活环境及状态的智能管理。系统以单片机为中枢,连接红外测温传感器,可实时精准捕捉宠物体温变化,以便及时发现健康异常;水位检测传感器时刻监测饮用水余量,防止宠物…...
