矩阵中严格递增的单元格数
题目链接:leetcode:矩阵中严格递增的单元格数
描述
给你一个下标从 1 开始、大小为 m x n 的整数矩阵 mat,你可以选择任一单元格作为 起始单元格 。
从起始单元格出发,你可以移动到 同一行或同一列 中的任何其他单元格,但前提是目标单元格的值 严格大于 当前单元格的值。
你可以多次重复这一过程,从一个单元格移动到另一个单元格,直到无法再进行任何移动。
请你找出从某个单元开始访问矩阵所能访问的 单元格的最大数量 。
返回一个表示可访问单元格最大数量的整数。
其中:
m == mat.length
n == mat[i].length
1 <= m, n <= 10^5
1 <= m * n <= 10^5
-10^5 <= mat[i][j] <= 10^5
输入
mat = [[3,1,6],[-9,5,7]]
输出
4
PS:之前有事漏做了ε=(´ο`*)))唉,今天补一下。
思路:
初看题目,位置(i, j),只能移动到同行或同列中值严格比他大的位置。因此可以将这个矩阵根据每个位置间的可到达性建立一张拓扑图,所求的得到最大单元格访问数量的路线,必然是从拓扑图中某一个入度为0的位置出发到某一个出度为0的位置结束。根据这个特性,我们可以从入度为0或者出度为0的位置出发来计算最大单元格访问数量。
在这里我采用了从出度为0出发的思路,个人感觉更“顺”一点。
设从位置(i , j)出发的最大单元格访问数为dp[i][j],(i, p)可表示所有同行中(i, j)可到达的位置,(q, j)可表示同列中(i , j)可到达的位置。那么dp[i][j] = max(max(dp[i][p]+1), max(dp[q][j]+1) ) 。从这里可以看出,要得到dp[i][j],我们要算出同行中所有的dp[i][p]和同列中所有的dp[q][j],所以我们要从拓扑图的右边往左边计算dp[i][j](最右边位置出度为0,dp[i][j] = 1)。
如果能顺利建图,那么问题就简单了,但是这里矩阵可能出现一维的情况,那么建图的复杂度就为O(n^2),对于n最大为1e5的情况显然会超时,所以还得优化思路。
不能建图,那就继续从小的只能往大的位置走这一特性入手,并从整体出发。只要我先计算了所有比位置(i, j)值大的位置的dp值,那么计算dp[i][j]所需的依赖——dp[i][p]和dp[q][j],都已经算好了。现在有了dp[i][p]和dp[q][j],就剩下max(dp[i][p])和max(dp[q][j])的计算。若每次都采用遍历的方法去计算max(dp[i][p])和max(dp[q][j]),总复杂度又回到了O(n^2),仍需优化。
以max(dp[i][p])的计算为例,若有两个位置(i, j0)和(i, j1), 且mat[i][j0] = mat[i][j1] + 1(只要mat[i][j1]是第i行中仅次于mat[i][j0]的值就行了),目前已知dp[i][j0],那么(i, j1)的max(dp[i][p]) = dp[i][j0] + 1。因此我们可建立两个数组,一个保存每行的最大dp值,一个保存每列的最大dp值。虽然我们是按mat值从大到小计算dp值,能保证不少算东西,但行或列中可能会存在相同的值,会多算东西。所以对于每行/每列的最大dp值需要存两个,一个存最大dp值一个存次大dp值,且取得两个值所在位置的mat值不能相同。这样就只需要在计算时比较一下mat[i][j]是否等于最大值所在mat值就行了,若不等于则选择最大dp值,反之选次大dp值。
struct node
{int val, x, y;bool operator < (const node &o)const{return val > o.val;}
};
struct dpnode
{int val_0, cnt_0;int val_1, cnt_1;void update(int val, int cnt){if(val == val_0){if(cnt > cnt_0){cnt_0 = cnt;}}else {if(cnt > cnt_0){cnt_1 = cnt_0;val_1 = val_0;cnt_0 = cnt;val_0 = val;}else if(cnt > cnt_1){cnt_1 = cnt;val_1 = val;}}}
};
const int inf = -1e5 - 5;
class Solution {
public:int maxIncreasingCells(vector<vector<int>>& mat) {int n = mat.size(), m = mat[0].size();vector<node> arr(n * m);dpnode demoe = (dpnode){inf, 0, inf, 0};vector<dpnode> row(n, demoe), col(m, demoe);for(int i = 0; i < n;i++){for(int j = 0;j < m;j++){arr[i*m+j] = (node){mat[i][j], i, j};}} sort(arr.begin(), arr.end());int ans=0;int tmp_row, tmp_col;for(int i = 0;i < arr.size();i++){if(row[arr[i].x].val_0 != arr[i].val){tmp_row = row[arr[i].x].cnt_0 + 1;}else tmp_row = row[arr[i].x].cnt_1 + 1;if(col[arr[i].y].val_0 != arr[i].val){tmp_col = col[arr[i].y].cnt_0 + 1;}else tmp_col = col[arr[i].y].cnt_1 + 1;if(tmp_col > tmp_row) tmp_row = tmp_col;row[arr[i].x].update(arr[i].val, tmp_row);col[arr[i].y].update(arr[i].val, tmp_row);}for(int i = 0;i < n;i++){ans = max(ans, row[i].cnt_0);}for(int j = 0;j < m;j++){ans = max(ans, col[j].cnt_0);}return ans;}
};
若有什么错误,欢迎指正^ _ ^ 。
相关文章:

矩阵中严格递增的单元格数
题目链接:leetcode:矩阵中严格递增的单元格数 描述 给你一个下标从 1 开始、大小为 m x n 的整数矩阵 mat,你可以选择任一单元格作为 起始单元格 。 从起始单元格出发,你可以移动到 同一行或同一列 中的任何其他单元格,但前提是目…...
)
超参数调优-通用深度学习篇(上)
文章目录 深度学习超参数调优网格搜索示例一:网格搜索回归模型超参数示例二:Keras网格搜索 随机搜索贝叶斯搜索 超参数调优框架Optuna深度学习超参数优化框架nvidia nemo大模型超参数优化框架 参数调整理论: 黑盒优化:超参数优化…...

小程序中data-xx是用方式
data-sts"3" 是微信小程序中的一种数据绑定语法,用于在 WXML(小程序模板)中将自定义的数据绑定到页面元素上。让我详细解释一下: data-xx 的作用: data-xx 允许你在页面元素上自定义属性,以便在事…...

【2024德国工作】外国人在德国找工作是什么体验?
挺难的,德语应该是所有中国人的难点。大部分中国人进德国公司要么是做中国业务相关,要么是做技术领域的工程师。先讲讲人在中国怎么找德国的工作,顺便延申下,德国工作的真实体验,最后聊聊在今年的德国工作签证申请条件…...

Unity中获取数据的方法
Input和GetComponent 一、Input 1、Input类: 用于处理用户输入(如键盘、鼠标、触摸等)的静态类 2、作用: 允许你检查用户的输入状态。如某个键是否被按下,鼠标的位置,触摸的坐标等 3、实例 (1) 键盘…...

Java的死锁问题
Java中的死锁问题是指两个或多个线程互相持有对方所需的资源,导致它们在等待对方释放资源时永久地阻塞的情况。 死锁产生条件 死锁发生通常需要满足以下四个必要条件: 互斥条件:至少有一个资源是只能被一个线程持有的,如果其他…...

Unity 公用函数整理【二】
1、在规定时间时间内将一个值变化到另一个值,使用Mathf.Lerp实现 private float timer;[Tooltip("当前温度")]private float curTemp;[Tooltip("开始温度")]private float startTemp 20;private float maxTemp 100;/// <summary>/// 升…...

千年古城的味蕾传奇-平凉锅盔
在甘肃平凉这片古老而神秘的土地上,有一种美食历经岁月的洗礼,依然散发着独特的魅力,那便是平凉锅盔。平凉锅盔,那可是甘肃平凉的一张美食名片。它外表金黄,厚实饱满,就像一轮散发着诱人香气的金黄月亮。甘…...
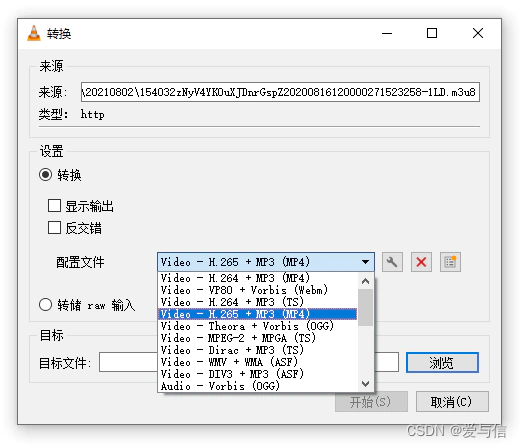
微信小程序视频如何下载
一、工具准备 1、抓包工具Fiddler Download Fiddler Web Debugging Tool for Free by Telerik 2、VLC media player Download official VLC media player for Windows - VideoLAN 3、微信PC端 微信 Windows 版 二、开始抓包 1、打开Fiddler工具,设置修改如下…...

SVN 安装教程
SVN 安装教程 SVN(Subversion)是一个开源的版本控制系统,广泛用于软件开发和文档管理。本文将详细介绍如何在不同的操作系统上安装SVN,包括Windows、macOS和Linux。 Windows系统上的SVN安装 1. 下载SVN 访问SVN官方网站或Visu…...

HTML静态网页成品作业(HTML+CSS)—— 家乡山西介绍网页(3个页面)
🎉不定期分享源码,关注不丢失哦 文章目录 一、作品介绍二、作品演示三、代码目录四、网站代码HTML部分代码 五、源码获取 一、作品介绍 🏷️本套采用HTMLCSS,未使用Javacsript代码,共有6个页面。 二、作品演示 三、代…...
:定理6的补充证明及三道循环置换例题)
【抽代复习笔记】20-群(十四):定理6的补充证明及三道循环置换例题
例1:找出S3中所有不能和(123)交换的元。 解:因为 (123)(1) (1)(123) (123),(123)(132) (132)(123) (1),所以(1)、(132)和(123)均可以交换; 而(12)(123) (23),(123)(12) (13),故 (12)(12…...
【单片机毕业设计选题24018】-基于STM32和阿里云的农业大棚系统
系统功能: 系统分为手动和自动模式,上电默认为自动模式,自动模式下系统根据采集到的传感器值 自动控制,温度过低后自动开启加热,湿度过高后自动开启通风,光照过低后自动开启补 光,水位过低后自动开启水泵…...

【计算机毕业设计】206校园顺路代送微信小程序
🙊作者简介:拥有多年开发工作经验,分享技术代码帮助学生学习,独立完成自己的项目或者毕业设计。 代码可以私聊博主获取。🌹赠送计算机毕业设计600个选题excel文件,帮助大学选题。赠送开题报告模板ÿ…...

9、PHP 实现调整数组顺序使奇数位于偶数前面
题目: 调整数组顺序使奇数位于偶数前面 描述: 输入一个整数数组,实现一个函数来调整该数组中数字的顺序,使得所有的奇数位于数组的前半部分, 所有的偶数位于位于数组的后半部分,并保证奇数和奇数ÿ…...
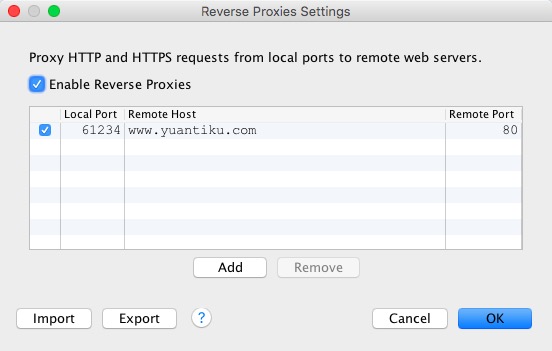
iOS开发工具-网络封包分析工具Charles
一、Charles简介 Charles 是在 Mac 下常用的网络封包截取工具,在做 移动开发时,我们为了调试与服务器端的网络通讯协议,常常需要截取网络封包来分析。 Charles 通过将自己设置成系统的网络访问代理服务器,使得所有的网络访问请求…...

7、PHP 实现矩形覆盖
题目: 矩形覆盖 描述: 我们可以用21的小矩形横着或者竖着去覆盖更大的矩形。 请问用n个21的小矩形无重叠地覆盖一个2*n的大矩形,总共有多少种方法? <?php function rectCover($number) {$prePreNum 1;$preNum 2;$temp 0;i…...
鸿蒙开发通信与连接:【@ohos.wifiext (WLAN)】
WLAN 说明: 本模块首批接口从API version 8开始支持。后续版本的新增接口,采用上角标单独标记接口的起始版本。 该文档中的接口只供非通用类型产品使用,如路由器等,对于常规类型产品,不应该使用这些接口。 导入模块 …...

Ps:脚本事件管理器
Ps菜单:文件/脚本/脚本事件管理器 Scripts/Script Events Manager 脚本事件管理器 Script Events Manager允许用户将特定的事件(如打开、存储或导出文件)与 JavaScript 脚本或 Photoshop 动作关联起来,以便在这些事件发生时自动触…...

redis哨兵模式下业务代码连接实现
目录 一:背景 二:实现过程 三:总结 一:背景 在哨兵模式下,真实的redis服务地址由一个固定ip转变为可以变化的ip,这样我们业务代码在连接redis的时候,就需要判断哪个主redis服务地址,哪个是从…...

网络编程(Modbus进阶)
思维导图 Modbus RTU(先学一点理论) 概念 Modbus RTU 是工业自动化领域 最广泛应用的串行通信协议,由 Modicon 公司(现施耐德电气)于 1979 年推出。它以 高效率、强健性、易实现的特点成为工业控制系统的通信标准。 包…...

浅谈 React Hooks
React Hooks 是 React 16.8 引入的一组 API,用于在函数组件中使用 state 和其他 React 特性(例如生命周期方法、context 等)。Hooks 通过简洁的函数接口,解决了状态与 UI 的高度解耦,通过函数式编程范式实现更灵活 Rea…...

国防科技大学计算机基础课程笔记02信息编码
1.机内码和国标码 国标码就是我们非常熟悉的这个GB2312,但是因为都是16进制,因此这个了16进制的数据既可以翻译成为这个机器码,也可以翻译成为这个国标码,所以这个时候很容易会出现这个歧义的情况; 因此,我们的这个国…...

MPNet:旋转机械轻量化故障诊断模型详解python代码复现
目录 一、问题背景与挑战 二、MPNet核心架构 2.1 多分支特征融合模块(MBFM) 2.2 残差注意力金字塔模块(RAPM) 2.2.1 空间金字塔注意力(SPA) 2.2.2 金字塔残差块(PRBlock) 2.3 分类器设计 三、关键技术突破 3.1 多尺度特征融合 3.2 轻量化设计策略 3.3 抗噪声…...

Cesium1.95中高性能加载1500个点
一、基本方式: 图标使用.png比.svg性能要好 <template><div id"cesiumContainer"></div><div class"toolbar"><button id"resetButton">重新生成点</button><span id"countDisplay&qu…...

什么是库存周转?如何用进销存系统提高库存周转率?
你可能听说过这样一句话: “利润不是赚出来的,是管出来的。” 尤其是在制造业、批发零售、电商这类“货堆成山”的行业,很多企业看着销售不错,账上却没钱、利润也不见了,一翻库存才发现: 一堆卖不动的旧货…...

Java-41 深入浅出 Spring - 声明式事务的支持 事务配置 XML模式 XML+注解模式
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

如何在最短时间内提升打ctf(web)的水平?
刚刚刷完2遍 bugku 的 web 题,前来答题。 每个人对刷题理解是不同,有的人是看了writeup就等于刷了,有的人是收藏了writeup就等于刷了,有的人是跟着writeup做了一遍就等于刷了,还有的人是独立思考做了一遍就等于刷了。…...

Java 二维码
Java 二维码 **技术:**谷歌 ZXing 实现 首先添加依赖 <!-- 二维码依赖 --><dependency><groupId>com.google.zxing</groupId><artifactId>core</artifactId><version>3.5.1</version></dependency><de…...

MySQL 知识小结(一)
一、my.cnf配置详解 我们知道安装MySQL有两种方式来安装咱们的MySQL数据库,分别是二进制安装编译数据库或者使用三方yum来进行安装,第三方yum的安装相对于二进制压缩包的安装更快捷,但是文件存放起来数据比较冗余,用二进制能够更好管理咱们M…...
