当前位置： 首页 > news >正文

PCL common中常见的基础功能函数

news 2026/2/11 0:29:12

文章目录

      • 一、common模块中的头文件
      • 二、common模块中的基本函数
        • 1、angles.h
        • 2、centroid.h
          • 1）计算给定一群点的3D中心点，并且返回一个三维向量
          • 2）计算给定的三维点云的协方差矩阵。
          • 3）计算正则化的3*3的协方差矩阵以及给定点云数据的中心点
          • 4）利用一组点的指数对其进行一般的、通用的nD中心估计。
        • 3、common.h
          • 1）计算两个向量之间的角度
          • 2）同时计算给定点云数据的均值和标准方差
          • 3）在给定边界的情况下，获取一组位于框中的点
          • 4）给定点云数据中点与点之间的最大距离的值
          • 5）获取给定点云中的在XYZ轴上的最大和最小值
          • 6）计算由三个点pa、pb和pc构成的三角形的外接圆半径。
          • 7）获取点直方图上的最小值和最大值。
          • 8）根据给定的多边形的点云计算多边形的面积
        • 4、copy_point.h
          • 1）从Point_in把字段数据赋值到Point_out
        • 5、distance.h
          • 1）获取两条三维直线之间的最短三维线段
          • 2）获取点到线的平方距离（由点和方向表示）
          • 3）在给定的一组点中获得最大分段，并返回最小和最大点。
        • 6、eigen.h
          • 1）确定最小特征值及其对应的特征向量
          • 2）确定对称半正定输入矩阵给定特征值对应的特征向量
          • 3）确定对称半正定输入矩阵最小特征值的特征向量和特征值
          • 4）计算2x2矩阵的逆。
          • 5）计算3x3对称矩阵的逆。
          • 6）计算3x3矩阵的行列式
          • 7）获得唯一 的3D旋转，将Z轴旋转成（0，0，1）Y轴旋转成（0,1,0）并且两个轴是正交的。
          • 11）得到将origin转化为（0，0，0）的变换，并将Z轴旋转成（0，0，1）和Y方向（0，1，0）
          • 12）从给定的变换矩阵中提取欧拉角
          • 13）给定的转换中，提取XYZ以及欧拉角
          • 14）从给定的平移和欧拉角创建转换矩阵
          • 15）保存或者写矩阵到一个输出流中
          • 16）从输入流中读取矩阵
        • 7、intersection.h
          • 1）获取空间中两条三维直线作为三维点的交点。
        • 8、io.h
          • 1）获取指定字段的索引（即维度/通道）
          • 2）获取给定点云中所有可用字段的列表
          • 3）获取特定字段数据类型的大小（字节）。
          • 4）连接 pcl::PCLPointCloud2类型的点云字段

pcl_common中主要是包含了 PCL库常用的公共数据结构和方法，比如 PointCloud的类和许多用于表示 点，曲面，法向量，特征描述等点的类型，用于计算距离，均值以及协方差，角度转换以及几何变化的函数。

对于各种点，特征的类型的数据结构在这里就不再一一举例说明，这需要根据实际情况而定。

这里主要介绍一下基本的常见的功能函数，这些函数其实用C++也可以自行实现，在PCL中提供了更多的重载接口，方便使用。

一、common模块中的头文件

angles.h 定义了标准的C接口的角度计算函数

centriod.h 定义了中心点的估算以及协方差矩阵的计算

commo.h 标准的C以及C++类，是其他common 函数的父类

copy_point.h 有一个简单的copy函数

distance.h 定义标准的C接口用于计算距离

eigen.h 一些线性代数函数

file_io.h 定义了一些文件帮助写或者读方面的功能。

random.h 定义一些随机点云生成的函数

geometry.h 定义一些基本的几何功能的函数

intersection.h 定义线与线相交的函数

norm.h 定义了标准的C方法计算矩阵的正则化

tim

相关文章：

PCL common中常见的基础功能函数

文章目录 一、common模块中的头文件二、common模块中的基本函数1、angles.h2、centroid.h1）计算给定一群点的3D中心点，并且返回一个三维向量2）计算给定的三维点云的协方差矩阵。3）计算正则化的3*3的协方差矩阵以及给定点云数据的中心点4）利用一组点的指数对其进行一般的、…...

编程日记 2024/6/22 11:45:14

力扣每日一题 6/22 字符串/贪心

博客主页：誓则盟约系列专栏：IT竞赛 专栏关注博主，后期持续更新系列文章如果有错误感谢请大家批评指出，及时修改感谢大家点赞👍收藏⭐评论✍ 2663.字典序最小的美丽字符串【困难】 题目： 如果一个字符串满…...

编程日记 2024/6/22 11:43:12

MCT Self-Refine：创新集成蒙特卡洛树搜索 （MCTS）提高复杂数学推理任务的性能，超GPT4，使用 LLaMa-3 8B 进行自我优化

📜 文献卡 题目： Accessing GPT-4 level Mathematical Olympiad Solutions via Monte Carlo Tree Self-refine with LLaMa-3 8B作者: Di Zhang; Xiaoshui Huang; Dongzhan Zhou; Yuqiang Li; Wanli OuyangDOI: 10.48550/arXiv.2406.07394摘要: This pape…...

编程日记 2024/6/22 11:42:11

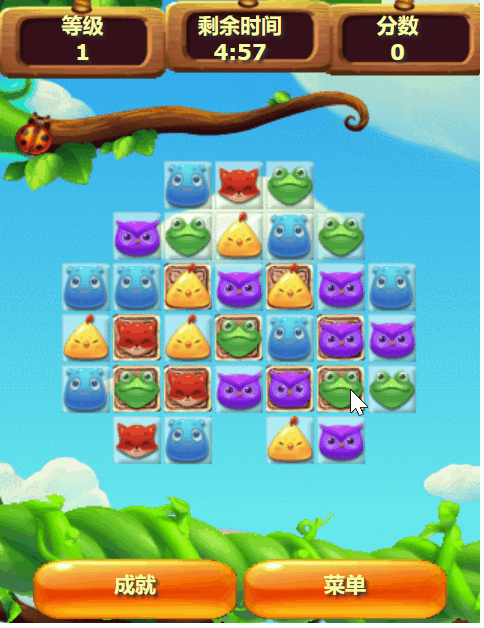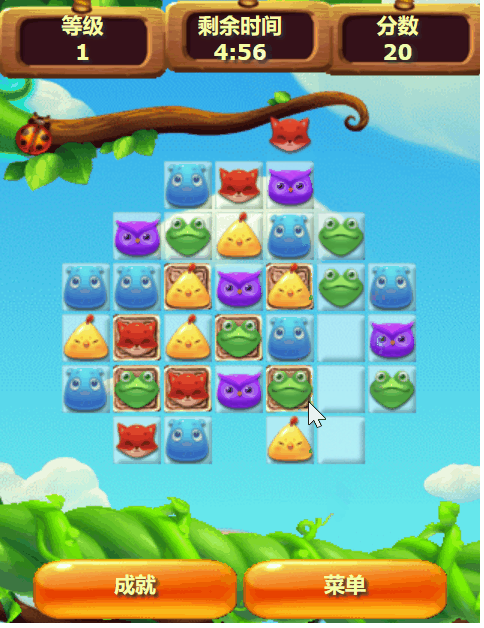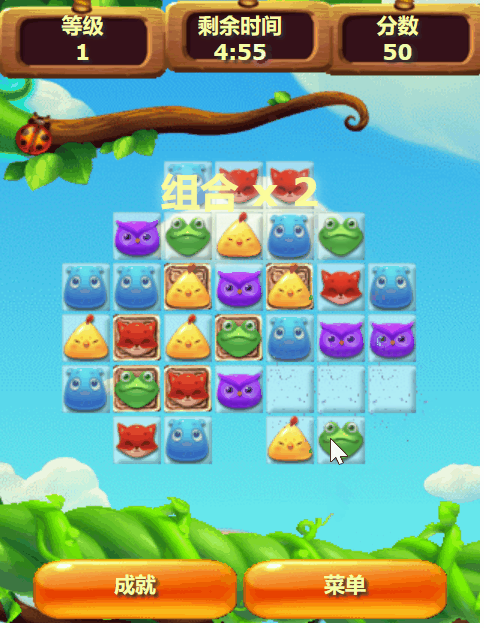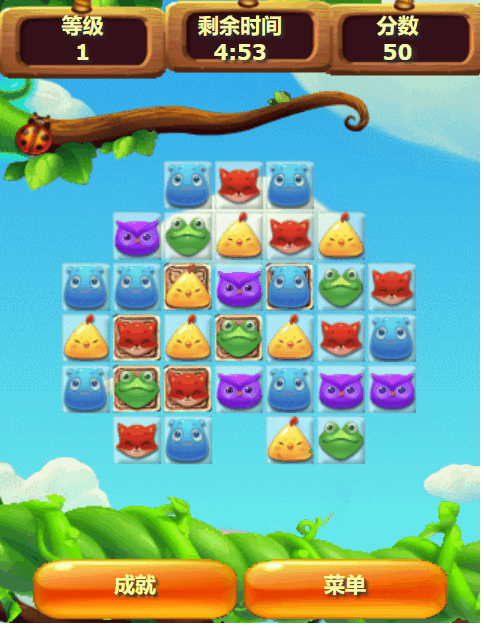
自制HTML5游戏《开心消消乐》

1. 引言 游戏介绍 《开心消消乐》是一款基于HTML5技术开发的网页游戏，以其简单的操作方式、轻松的游戏体验和高度的互动性，迅速在社交平台上获得了广泛的关注和传播。玩家通过消除相同类型的元素来获得分数，游戏设计巧妙，易于上手…...

编程日记 2024/6/22 11:40:08

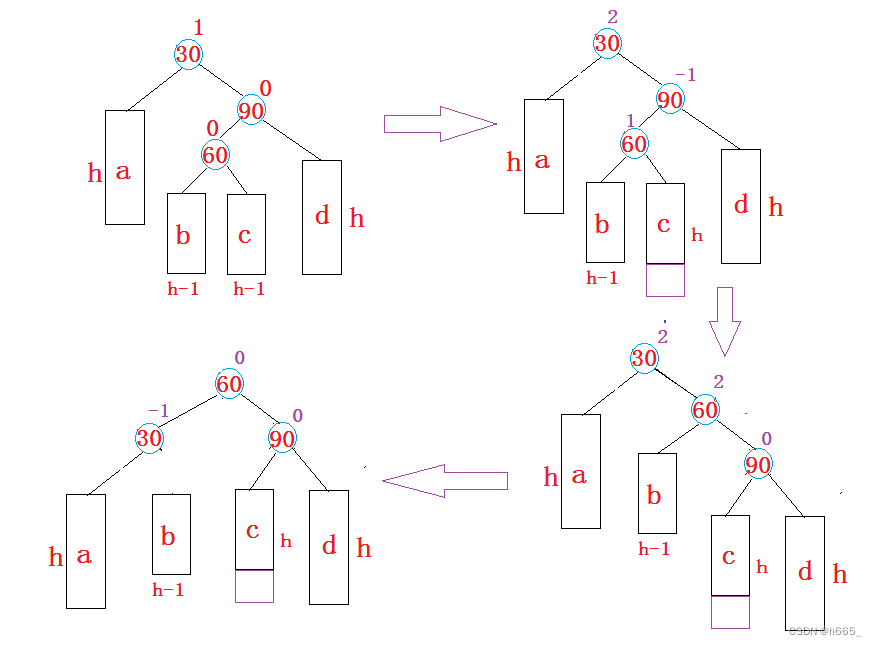
【C++】平衡二叉树(AVL树)的实现

目录 一、AVL树的概念二、AVL树的实现1、AVL树的定义2. 平衡二叉树的插入2.1 按照二叉排序树的方式插入并更新平衡因子2.2 AVL树的旋转2.2.1 新节点插入较高左子树的左侧（LL平衡旋转）2.2.2 新节点插入较高右子树的右侧（RR平衡旋转&#xff09…...

编程日记 2024/6/22 11:39:07

第一百一十八节 Java面向对象设计 - Java接口

Java面向对象设计 - Java接口 什么是接口？ Java中的接口定义了一个引用类型来创建抽象概念。接口由类实现以提供概念的实现。 在Java 8之前，一个接口只能包含抽象方法。 Java 8允许接口具有实现的静态和默认方法。 接口通过抽象概念定义不相关类之间…...

编程日记 2024/6/22 11:38:05

Flink nc -l -p 监听端口测试

1、9999端口未占用 netstat -apn|grep 99992、消息发送端 nc -l -k -p 9999 {"user":"ming","url":"www.baidu1.com", "timestamp":1200L, "score":1} {"user":"xiaohu","url":…...

编程日记 2024/6/22 11:37:04

在IntelliJ IDEA中使用Spring Boot：快速配置

使用IntelliJ IDEA开发Spring Boot应用程序可以极大地提高开发效率，因为IDEA提供了许多便捷的功能，比如自动补全、代码分析、热部署等。以下是一篇可能的CSDN博客文章草稿，介绍如何在IntelliJ IDEA中使用Spring Boot： 在IntelliJ …...

编程日记 2024/6/22 11:36:03

django filter 批量修改

django filter 批量修改 在Django中，如果你想要批量修改记录，可以使用update()方法。这个方法允许你在一个查询集上执行批量更新，而不需要为每条记录生成单独的数据库事务。 以下是一个使用update()方法批量修改记录的例子： fro…...

编程日记 2024/6/22 11:35:02

maven:中央仓库验证方式改变：401 Content access is protected by token

前几天向maven中央仓库发布版本，执行上传命令mvn release:perform时报错了： [ERROR] Failed to execute goal org.sonatype.plugins:nexus-staging-maven-plugin:1.6.13:deploy (injected-nexus-deploy) on project xxxxx: Failed to deploy artifacts: …...

编程日记 2024/6/22 11:31:58

【面试】http

一、定义 HTTP（超文本传输协议），是一种用于分布式、协作式、超媒体信息系统的应用层协议，它是万维网数据通信的基础。主要特点是无状态（服务器不会保存之前请求的状态）、无连接（服务器处理完请…...

编程日记 2024/6/22 11:28:55

获取泛型，泛型擦除，TypeReference 原理分析

说明 author blog.jellyfishmix.com / JellyfishMIX - githubLICENSE GPL-2.0 获取泛型，泛型擦除 下图中示例代码是一个工具类用于生成 csv 文件，需要拿到数据的类型，使用反射感知数据类型的字段，来填充表字段名。可以看到泛型…...

编程日记 2024/6/22 11:27:54

springboot 3.x 之 集成rabbitmq实现动态发送消息给不同的队列

背景 实际项目中遇到针对不同类型的消息，发送消息到不同的队列，而且队列可能还不存在，需要动态创建，于是写了如下代码，实践发现没啥问题，这里分享下。 环境 springboot 3.2 JDK 17 rabbitMQ模型介绍 图片…...

编程日记 2024/6/22 11:25:51

C++ 代码实现鼠标右键注册菜单，一级目录和二级目录方法

最近做的一个项目， 在使用windows的时候，我希望在右键菜单中添加一个自定义的选项， 该选项下有我经常使用的多个程序快捷方式， 直接上代码 头文件 #pragma once #include <Windows.h> #include <iostream> #include <string> using namespace std; …...

编程日记 2024/6/22 11:24:50

SQLite 3 优化批量数据存储操作---事务transaction机制

0、事务操作 事务的目的是为了保证数据的一致性和完整性。 事务&#xff08;Transaction&#xff09;具有以下四个标准属性&#xff0c;通常根据首字母缩写为 ACID&#xff1a; 原子性&#xff08;Atomicity&#xff09;&#xff1a;确保工作单位内的所有操作都成功完成&…...

编程日记 2024/6/22 11:23:49

[程序员] 表达的能力

之前看CSDN的问答区&#xff0c;很多时候&#xff0c;感觉问题的描述所要表达的意思非常模糊&#xff0c;或者说描述不清。如果是想回答问题的人想回答问题&#xff0c;首先要搞清楚是什么问题&#xff0c;就需要再问问题主很多细节的东西。三来四去&#xff0c;才能搞清楚具体…...

编程日记 2024/6/22 11:22:48

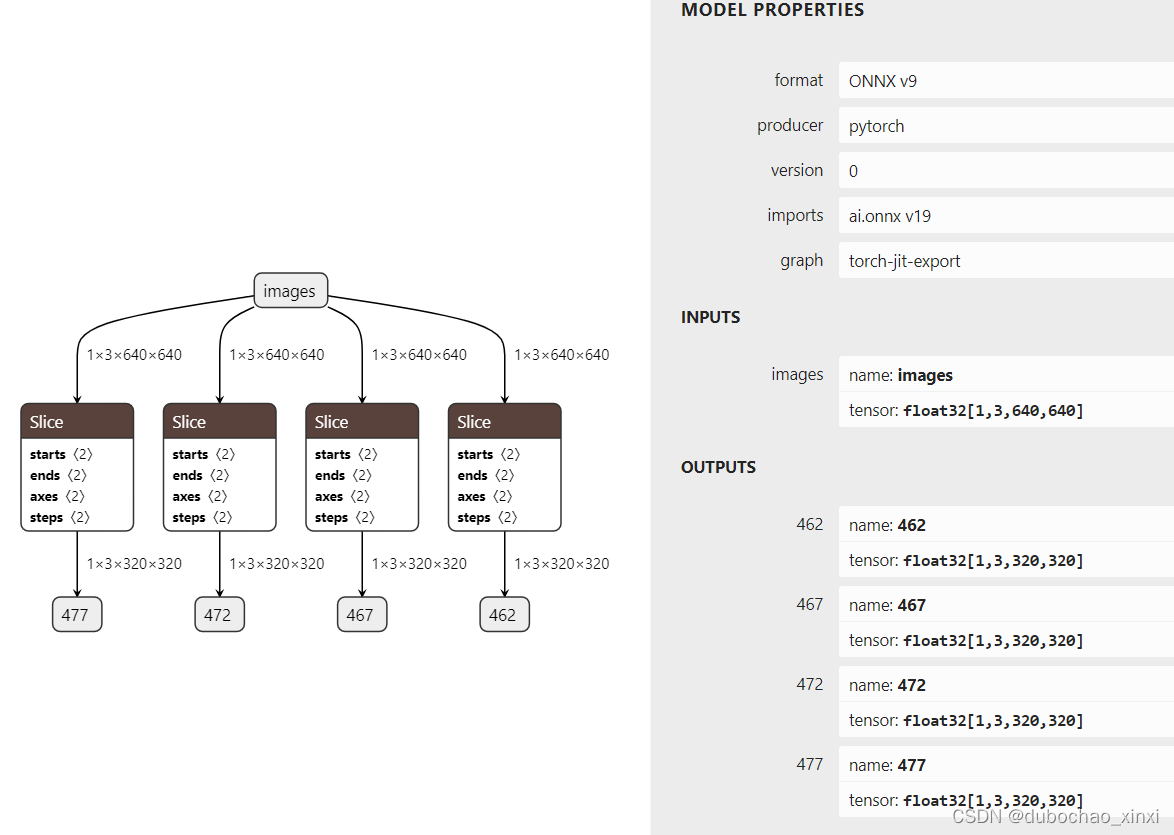
rknn转换后精度差异很大，失真算子自纠

下面是添加了详细注释的优化代码&#xff1a; import cv2 import numpy as np import onnx import onnxruntime as rt from onnx import helper, shape_inferencedef get_all_node_names(model):"""获取模型中所有节点的名称。参数:model (onnx.ModelProto): O…...

编程日记 2024/6/22 11:21:47

【C语言】解决C语言报错：Stack Overflow

文章目录 简介什么是Stack OverflowStack Overflow的常见原因如何检测和调试Stack Overflow解决Stack Overflow的最佳实践详细实例解析示例1&#xff1a;递归调用过深示例2&#xff1a;分配过大的局部变量示例3&#xff1a;嵌套函数调用过多 进一步阅读和参考资料总结 简介 St…...

编程日记 2024/6/22 11:14:40

【滚动哈希 二分查找】1044. 最长重复子串

本文涉及知识点 滚动哈希 二分查找算法合集 LeetCode 1044. 最长重复子串 给你一个字符串 s &#xff0c;考虑其所有 重复子串 &#xff1a;即 s 的&#xff08;连续&#xff09;子串&#xff0c;在 s 中出现 2 次或更多次。这些出现之间可能存在重叠。 返回 任意一个 可能具…...

编程日记 2024/6/22 11:13:39

webid、sec_poison_id、a1、web_session参数分析与算法实现

文章目录 1. 写在前面2. 参数分析3. 核心算法【🏠作者主页】：吴秋霖 【💼作者介绍】：擅长爬虫与JS加密逆向分析！Python领域优质创作者、CSDN博客专家、阿里云博客专家、华为云享专家。一路走来长期坚守并致力于Python与爬虫领域研究与开发工作！ 【🌟作者推荐】：对爬…...

编程日记 2024/6/22 11:12:38

springboot 百货中心供应链管理系统小程序

一、前言 随着我国经济迅速发展&#xff0c;人们对手机的需求越来越大&#xff0c;各种手机软件也都在被广泛应用&#xff0c;但是对于手机进行数据信息管理&#xff0c;对于手机的各种软件也是备受用户的喜爱&#xff0c;百货中心供应链管理系统被用户普遍使用&#xff0c;为方…...

编程新知 2026/2/8 20:41:49

python/java环境配置

环境变量放一起 python&#xff1a; 1.首先下载Python Python下载地址&#xff1a;Download Python | Python.org downloads ---windows -- 64 2.安装Python 下面两个&#xff0c;然后自定义&#xff0c;全选 可以把前4个选上 3.环境配置 1&#xff09;搜高级系统设置 2…...

编程新知 2026/2/9 15:41:39

Java多线程实现之Callable接口深度解析

Java多线程实现之Callable接口深度解析 一、Callable接口概述1.1 接口定义1.2 与Runnable接口的对比1.3 Future接口与FutureTask类 二、Callable接口的基本使用方法2.1 传统方式实现Callable接口2.2 使用Lambda表达式简化Callable实现2.3 使用FutureTask类执行Callable任务 三、…...

编程新知 2026/1/25 6:36:06

【Go语言基础【13】】函数、闭包、方法

文章目录 零、概述一、函数基础1、函数基础概念2、参数传递机制3、返回值特性3.1. 多返回值3.2. 命名返回值3.3. 错误处理 二、函数类型与高阶函数1. 函数类型定义2. 高阶函数&#xff08;函数作为参数、返回值&#xff09; 三、匿名函数与闭包1. 匿名函数&#xff08;Lambda函…...

编程新知 2025/12/8 19:02:25

C/C++ 中附加包含目录、附加库目录与附加依赖项详解

在 C/C 编程的编译和链接过程中&#xff0c;附加包含目录、附加库目录和附加依赖项是三个至关重要的设置&#xff0c;它们相互配合&#xff0c;确保程序能够正确引用外部资源并顺利构建。虽然在学习过程中&#xff0c;这些概念容易让人混淆&#xff0c;但深入理解它们的作用和联…...

编程新知 2026/1/26 2:22:24

群晖NAS如何在虚拟机创建飞牛NAS

套件中心下载安装Virtual Machine Manager 创建虚拟机 配置虚拟机 飞牛官网下载 https://iso.liveupdate.fnnas.com/x86_64/trim/fnos-0.9.2-863.iso 群晖NAS如何在虚拟机创建飞牛NAS - 个人信息分享...

编程新知 2026/1/30 6:19:54

MacOS下Homebrew国内镜像加速指南（2025最新国内镜像加速）

macos brew国内镜像加速方法 brew install 加速formula.jws.json下载慢加速 &#x1f37a; 最新版brew安装慢到怀疑人生&#xff1f;别怕&#xff0c;教你轻松起飞&#xff01; 最近Homebrew更新至最新版&#xff0c;每次执行 brew 命令时都会自动从官方地址 https://formulae.…...

编程新知 2026/1/28 10:57:16

恶补电源：1.电桥

一、元器件的选择 搜索并选择电桥&#xff0c;再multisim中选择FWB&#xff0c;就有各种型号的电桥: 电桥是用来干嘛的呢&#xff1f; 它是一个由四个二极管搭成的“桥梁”形状的电路&#xff0c;用来把交流电&#xff08;AC&#xff09;变成直流电&#xff08;DC&#xff09;。…...

编程新知 2026/2/9 5:44:35

pgsql：还原数据库后出现重复序列导致“more than one owned sequence found“报错问题的解决

问题&#xff1a; pgsql数据库通过备份数据库文件进行还原时&#xff0c;如果表中有自增序列&#xff0c;还原后可能会出现重复的序列&#xff0c;此时若向表中插入新行时会出现“more than one owned sequence found”的报错提示。 点击菜单“其它”-》“序列”&#xff0c;…...

编程新知 2026/2/9 22:03:57

Docker、Wsl 打包迁移环境

电脑需要开启wsl2 可以使用wsl -v 查看当前的版本 wsl -v WSL 版本&#xff1a; 2.2.4.0 内核版本&#xff1a; 5.15.153.1-2 WSLg 版本&#xff1a; 1.0.61 MSRDC 版本&#xff1a; 1.2.5326 Direct3D 版本&#xff1a; 1.611.1-81528511 DXCore 版本&#xff1a; 10.0.2609…...

编程新知 2025/10/14 5:08:48