算法:渐进记号的含义及时间复杂度计算
渐进记号及时间复杂度计算
- 渐近符号
- 时间复杂度计算:递归方程
- 代入法
- 迭代法
- 套用公式法
渐近符号
渐近记号 Ω \Omega Ω
f ( n ) = Ω ( g ( n ) ) f(n)=\Omega(g(n)) f(n)=Ω(g(n)) 当且仅当存在正的常数C和 n 0 n_0 n0,使得对于所有的 n ≥ n 0 n≥ n_0 n≥n0 ,有 f ( n ) ≥ C ( g ( n ) ) f(n)≥C(g(n)) f(n)≥C(g(n))。此时,称 g ( n ) g(n) g(n)是 f ( n ) f(n) f(n)的下界。
根据符号 Ω \Omega Ω的定义,用它评估算法的复杂度得到的是问题规模充分大时的一个下界。这个下界的阶越高,评估越精确,越有价值。
例:设 f ( n ) = n 2 + n f(n)=n^2+n f(n)=n2+n,则
f ( n ) = Ω ( n 2 ) f(n)=\Omega(n^2) f(n)=Ω(n2),取 c = 1 , n 0 = 1 c=1,n_0=1 c=1,n0=1 即可
f ( n ) = Ω ( 100 n ) f(n)=\Omega(100n) f(n)=Ω(100n),取 c = 1 / 100 , n 0 = 1 c=1/100,n_0=1 c=1/100,n0=1 即可
显然, Ω ( n 2 ) \Omega(n^2) Ω(n2)作为下界更为精确。
渐进记号 Θ \Theta Θ
f ( n ) = Θ ( g ( n ) ) f(n)=\Theta(g(n)) f(n)=Θ(g(n)) 当且仅当存在正常数和 C 1 , C 2 , n 0 C_1,C_2,n_0 C1,C2,n0,使得对于所有的 n ≥ n 0 n≥n_0 n≥n0, 有 C 1 ( g ( n ) ) ≤ f ( n ) ≤ C 2 ( g ( n ) ) C_1(g(n))≤f(n)≤ C_2(g(n)) C1(g(n))≤f(n)≤C2(g(n))。此时,称 f ( n ) f(n) f(n)与 g ( n ) g(n) g(n)同阶。
这种渐进符号是指,当问题规模足够大的时候,算法的运行时间将主要取决于时间表达式的第一项,其它项的执行时间可以忽略不计。第一项的常数系数,随着n的增大,对算法的执行时间也变得不重要了。
例: 3 n + 2 = Θ ( n ) 3n+2= Θ(n) 3n+2=Θ(n)
10 n 2 + 4 n + 2 = Θ ( n 2 ) 10n^2+4n+2= Θ(n^2) 10n2+4n+2=Θ(n2)
5 × 2 n + n 2 = Θ ( 2 n ) 5×2^n+n^2= Θ(2^n) 5×2n+n2=Θ(2n)
渐进记号小 ο \omicron ο
f ( n ) = ο ( g ( n ) ) f(n)=\omicron(g(n)) f(n)=ο(g(n))当且仅当 f ( n ) = ο ( g ( n ) ) f(n)=\omicron(g(n)) f(n)=ο(g(n))和 g ( n ) ≠ ο ( f ( n ) ) g(n)\neq \omicron(f(n)) g(n)=ο(f(n)),此时, g ( n ) g(n) g(n)是 f ( n ) f(n) f(n)的一个绝对上界。
小 ο \omicron ο提供的上界可能是渐近紧确的,也可能是非紧确的。(如: 2 n 2 = ο ( n 2 ) 2n^2=\omicron(n^2) 2n2=ο(n2)是渐近紧确的,而 2 n = ο ( n 2 ) 2n=\omicron(n^2) 2n=ο(n2)是非紧确上界。
例: 4 n l o g n + 7 = ο ( n 2 ) 4nlogn + 7= \omicron(n^2) 4nlogn+7=ο(n2)
渐进记号小 ω \omega ω
f ( n ) = ω ( g ( n ) ) f(n)=\omega(g(n)) f(n)=ω(g(n))当且仅当 f ( n ) = ω ( g ( n ) ) f(n)=\omega(g(n)) f(n)=ω(g(n))和 g ( n ) ≠ ω ( f ( n ) ) g(n)\neq \omega(f(n)) g(n)=ω(f(n)),此时, g ( n ) g(n) g(n)是 f ( n ) f(n) f(n)的一个绝对下界。
ω \omega ω表示一个非渐进紧确的下界。
例: f ( n ) = n 2 + n f(n)=n^2+n f(n)=n2+n,则 f ( n ) = f(n)= f(n)=\omega ( n ) (n) (n)是正确的, f ( n ) = f(n)= f(n)=\omega ( n 2 ) (n^2) (n2)是错误的。
渐进记号大 O \Omicron O
设 f ( n ) f(n) f(n)和 g ( n ) g(n) g(n) 是定义域为自然数集上的函数。若存在正数 c c c和 n 0 n_0 n0c和n_0c,使得对一切 n ≥ n 0 n≥ n_0 n≥n0 都有 0 ≤ f ( n ) ≤ c g ( n ) 0 ≤ f(n) ≤ cg(n) 0≤f(n)≤cg(n)成立,则称 f ( n ) f(n) f(n)的渐进的上界是 g ( n ) g(n) g(n),记作 f ( n ) = O g ( n ) f(n)=\Omicron g(n) f(n)=Og(n)。
根据符号大 O \Omicron O的定义,用它评估算法的复杂度得到的只是问题规模充分大时的一个上界。这个上界的阶越低,评估越精确,越有价值。
例:设 f ( n ) = n 2 + n f(n)=n^2+n f(n)=n2+n,有
f ( n ) = O ( n 2 ) f(n)=\Omicron(n^2) f(n)=O(n2),取 c = 2 , n 0 = 1 c=2,n_0=1 c=2,n0=1即可
f ( n ) = O ( n 3 ) f(n)=\Omicron(n^3) f(n)=O(n3),取 c = 1 , n 0 = 2 c=1,n_0=2 c=1,n0=2即可
常见的时间复杂度关系
O(1)<O(log(n))<O(n)<O(nlogn)<O(n^{2})
O ( 2 n ) O(2^{n}) O(2n)和 O ( n ! ) O(n!) O(n!)大于以上的所有时间复杂度,具体原因参考图像。
时间复杂度计算:递归方程
加、减、乘、除、比较、赋值等操作,一般被看作是基本操作,并约定所用的时间都是一个单位时间;通过计算这些操作分别执行了多少次来确定程序总的执行步数。一般来说,算法中关键操作的执行次数决定了算法的时间复杂度。
比较简单的算法时间复杂性估计通常需要观察在for、while循环中的关键操作执行次数,在这里我们只讨论一种比较复杂的时间复杂度计算问题:求递归方程解的渐近阶的方法。递归式就是一个等式,代表了递归算法运算时间和n的关系,通过更小输入的函数值来描述一个函数。那么如何求得递归算法的Θ渐进界呢?主要有三种方法。
代入法
代入法是指自己猜测一个界,然后用数学归纳法进行验证是否正确,这种猜测主要靠经验,不常用。
迭代法
迭代法是指循环地展开递归方程,然后把递归方程转化为和式,使用求和技术解之。
套用公式法
这个方法为估计形如: T ( n ) = a T ( n / b ) + f ( n ) T(n)=aT(n/b)+f(n) T(n)=aT(n/b)+f(n) 的递归方程解的渐近阶提供三个可套用的公式。要求其中的a≥1和b>1是常数,f(n)是一个确定的正函数。那么在三种情况下,我们可以得到T(n)的渐进估计式,懒得打公式,所以截图。
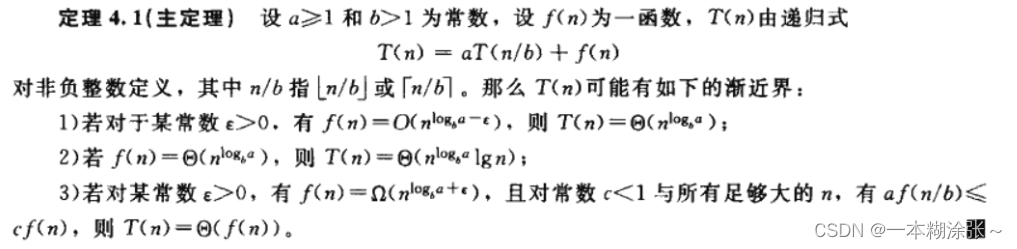
相关文章:
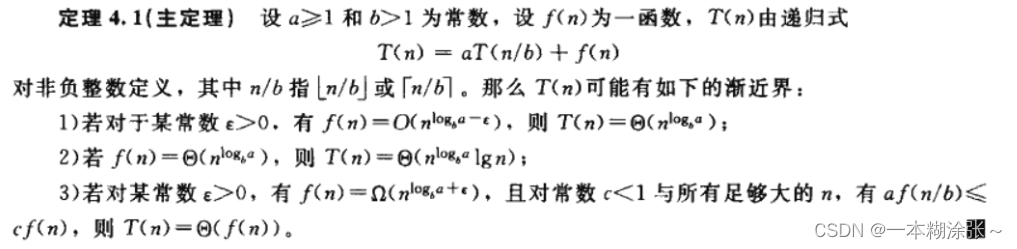
算法:渐进记号的含义及时间复杂度计算
渐进记号及时间复杂度计算 渐近符号渐近记号 Ω \Omega Ω渐进记号 Θ \Theta Θ渐进记号小 ο \omicron ο渐进记号小 ω \omega ω渐进记号大 O \Omicron O常见的时间复杂度关系 时间复杂度计算:递归方程代入法迭代法套用公式法 渐近符号 渐近记号 Ω \Omega Ω …...

idea导入文件里面的子模块maven未识别处理解决办法
1、File → Project Structure → 点击“Modules” → 点击“” → “Import Model” 2、可以看到很多子模块,选择子模块下的 pom.xml 文件导入一个一个点累死了,父目录下也没有pom文件 解决办法:找到子模块中有一个pom.xml文件,…...

IOS Swift 从入门到精通:协议和扩展
文章目录 协议协议继承扩展协议扩展面向协议的编程总结: 今天你将学习一些真正的 Swifty 功能:协议和面向协议的编程(POP)。 POP 摒弃了庞大而复杂的继承层次结构,代之以更小、更简单、可以组合在一起的协议。这确实应…...

Vue插件开发:Vue.js的插件架构允许开发者扩展Vue的核心功能,我们可以探讨如何开发一个Vue插件并与社区分享
了解Vue插件 Vue插件的概念: Vue插件用于为Vue.js添加全局级别的功能。它提供了一种开箱即用的机制来应用全局性的功能扩展。这些插件通常用来将全局方法或属性,组件选项,Vue实例的方法,或者注入一些组件选项比如mixins和自定义方法添加至Vue.js。 Vue插件的使用场景:…...

学习面向对象前--Java基础练习题
前言 写给所有一起努力学习Java的朋友们,敲代码本身其实是我们梳理逻辑的一个过程。我们在学习Java代码的过程中,除了需要学习Java的一些基本操作及使用,更重要的是我们需要培养好的逻辑思维。逻辑梳理好之后,我们编写代码实现需要…...
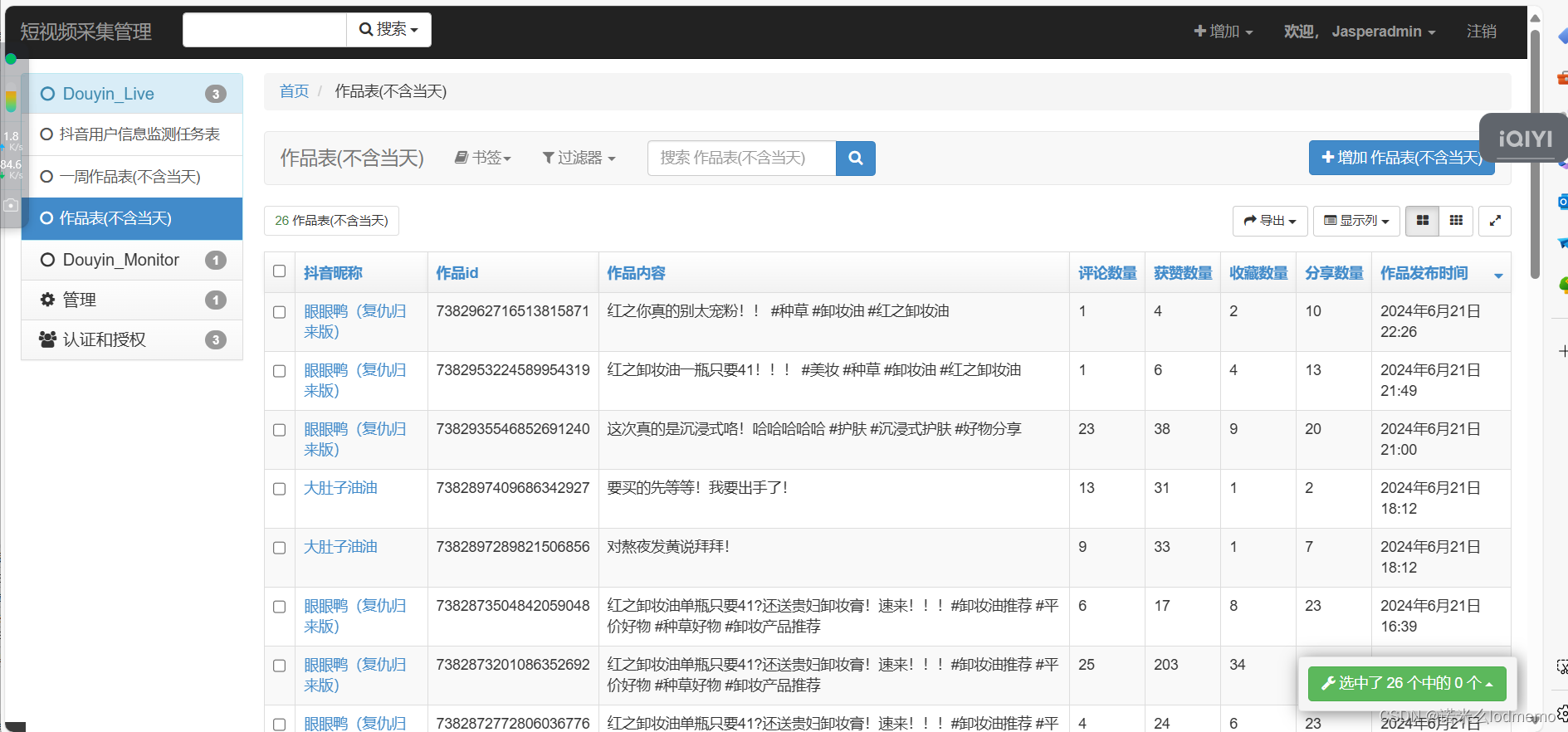
用Python实现抖音新作品监控助手,实时获取博主动态
声明: 本文以教学为基准、本文提供的可操作性不得用于任何商业用途和违法违规场景。本人对任何原因在使用本人中提供的代码和策略时可能对用户自己或他人造成的任何形式的损失和伤害不承担责任。包含关注,点赞等 该项目的主要功能是通过Python代码&…...

图像分隔和深度成像技术为什么受市场欢迎-数字孪生技术和物联网智能汽车技术的大爆发?分析一下图像技术的前生后世
图像分隔和深度成像是计算机视觉和图像处理领域的两项重要技术,它们各自有不同的技术基础和要点。 图像分隔技术基础: 机器学习和模式识别: 图像分隔通常依赖于机器学习算法,如支持向量机(SVM)、随机森林…...
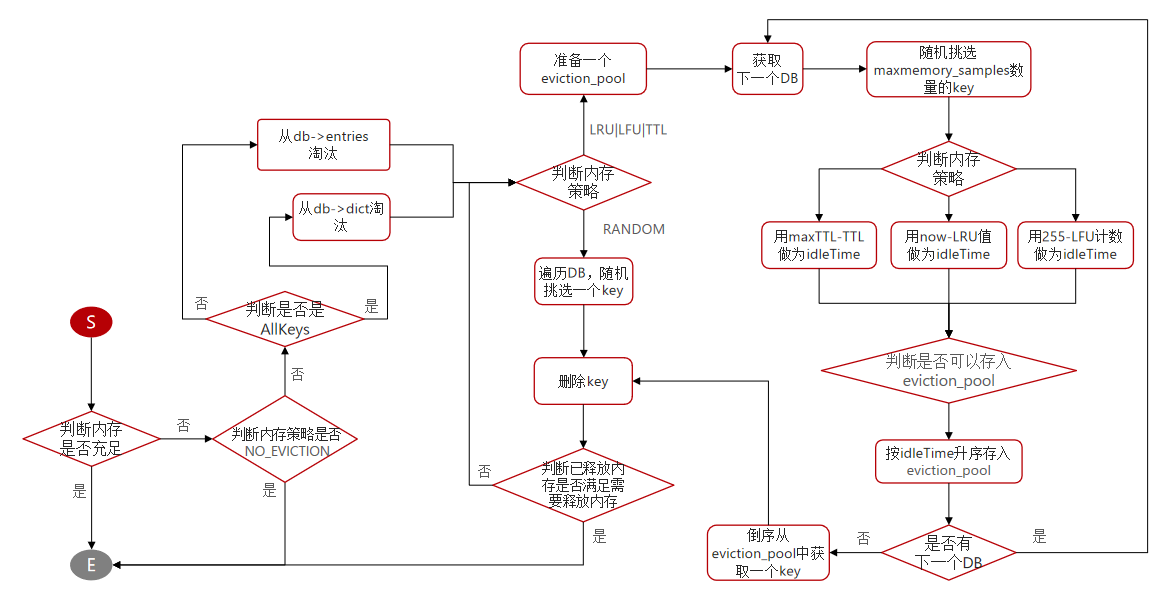
Redis 内存策略
一、Redis 内存回收 Redis 之所以性能强,最主要的原因就是基于内存存储。然而单节点的 Redis 其内存大小不宜过大,会影响持久化或主从同步性能。 我们可以通过修改配置文件来设置 Redis 的最大内存: # 格式: # maxmemory <byt…...

Java小实验————斗地主
早期使用的JavaSE用到的技术栈有:Map集合,数组,set集合,只是简单实现了斗地主的模拟阶段,感兴趣的小伙伴可以调试增加功能 代码如下: import java.util.*;public class Poker {public static void main(String[] arg…...
系统 CentOS7.6)
【Oracle】Linux 卸载重装 oracle 教程(如何清理干净残留)系统 CentOS7.6
总览 1.停止监听 2.删除 Oracle 数据库实例 3.删除 Oracle 相关服务 4.删除 Oracle 服务脚本 5.清理 Oracle 软件和配置文件 6.强制卸载 Oracle 软件包 一、开始干活(所有操作使用 root 权限,在 root 用户下执行) 1.停止监听 lsnrctl sto…...

web中间件漏洞-Jenkins漏洞-弱口令、反弹shell
web中间件漏洞-Jenkins漏洞-弱口令、反弹shell Jenkins弱口令 默认用户一般为jenkins/jenkins 使用admin/admin123登陆成功 Jenkins反弹shell 格式为 println"命令".execute().text 在/tmp目录中生成shell.sh文件,并向其中写入反弹shell的语句 new…...
)
Linux开发讲课9--- Linux的IPC机制-内存映射(Memory Mapping)
Linux的IPC(Inter-Process Communication,进程间通信)机制是多个进程之间相互沟通的方法,它允许不同进程之间传播或交换信息。Linux支持多种IPC方式,包括但不限于: 管道(Pipe)&#…...

Java赋值运算符
Java赋值运算符分为以下: 符号 作用 说明 赋值 int a 10,把10赋值给变量a 加后赋值 ab,将ab的值赋值给变量a - 减后赋值 a-b,将a-b的值赋值给变量a* 乘后赋值 a*b,将a*b的值赋值给变量a / 除后赋值 a/b,将a/b的值赋值给变量a % 取余赋值 a%b,将a%b的值赋值给变量…...
Qt做群控系统
群控系统顾名思义,一台设备控制多台机器。首先我们来创造下界面。我们通过QT UI设计界面。设计界面如下: 登录界面: 登录界面分为两种角色,一种是管理员,另一种是超级管理员。两种用户的主界面是不同的。通过选中记住…...

【专业英语 复习】第10章 Information System
1. 单选题 (1分) An example of this type of report would be a sales report that shows that certain items are selling significantly above or below forecasts. () A. Inventory B. Demand C. Periodic D. Exception 正确答案: D 这种类型的报…...

09-axios在Vue中的导入与配置
09-axios 前言首先简单了解什么是Axios?以上完成后就可以使用了 前言 我们接着上一篇文章 08-路由地址的数据获取 来讲。 下一篇文章 10-vuex在Vue中的导入与配置 首先简单了解什么是Axios? Axios是一个基于Promise 用于浏览器和 nodejs 的 HTTP 客户端…...
odoo17 小变更4
odoo17 小变更4 1、代码中去除了访问私人地址权限,但翻译中均还有,怪不 model:res.groups,name:base.group_private_addresses msgid "Access to Private Addresses" msgstr "" 代码也查看了,的确没有了此权限组 --><record model="res.g…...

Flink assignTimestampsAndWatermarks 深度解析:时间语义与水印生成
目录 概述 时间语义 时间戳分配 水印的作用 最佳实践 案例分析 注意事项 应用场景 概述 在Apache Flink中,assignTimestampsAndWatermarks是一个重要的方法,它允许数据流处理程序根据事件时间(event time)分配时间戳和生成水印(watermarks)。这个方法通常用于处理…...

C++排序算法——合并有序数组
合并有序数组 思路 我们可以设想一个排序的函数 这个函数里 我们有三个while while(第一次的执行条件) {先进行第一次的合并 } while(第二次的合并条件) { 把a数组在第一次没有排序上的给加进去 }while(第三次的合并条件) { 把b数组在第一次没有排序上的给加进去 }看完了这个…...

安装pytorch环境
安装:Anaconda3 通过命令行查显卡nvidia-smi 打开Anacanda prompt 新建 conda create -n pytorch python3.6 在Previous PyTorch Versions | PyTorch选择1.70,安装成功,但torch.cuda.is_available 返回false conda install pytorch1.7.0…...

Mac软件卸载指南,简单易懂!
刚和Adobe分手,它却总在Library里给你写"回忆录"?卸载的Final Cut Pro像电子幽灵般阴魂不散?总是会有残留文件,别慌!这份Mac软件卸载指南,将用最硬核的方式教你"数字分手术"࿰…...

Robots.txt 文件
什么是robots.txt? robots.txt 是一个位于网站根目录下的文本文件(如:https://example.com/robots.txt),它用于指导网络爬虫(如搜索引擎的蜘蛛程序)如何抓取该网站的内容。这个文件遵循 Robots…...

Fabric V2.5 通用溯源系统——增加图片上传与下载功能
fabric-trace项目在发布一年后,部署量已突破1000次,为支持更多场景,现新增支持图片信息上链,本文对图片上传、下载功能代码进行梳理,包含智能合约、后端、前端部分。 一、智能合约修改 为了增加图片信息上链溯源,需要对底层数据结构进行修改,在此对智能合约中的农产品数…...

Redis:现代应用开发的高效内存数据存储利器
一、Redis的起源与发展 Redis最初由意大利程序员Salvatore Sanfilippo在2009年开发,其初衷是为了满足他自己的一个项目需求,即需要一个高性能的键值存储系统来解决传统数据库在高并发场景下的性能瓶颈。随着项目的开源,Redis凭借其简单易用、…...

苹果AI眼镜:从“工具”到“社交姿态”的范式革命——重新定义AI交互入口的未来机会
在2025年的AI硬件浪潮中,苹果AI眼镜(Apple Glasses)正在引发一场关于“人机交互形态”的深度思考。它并非简单地替代AirPods或Apple Watch,而是开辟了一个全新的、日常可接受的AI入口。其核心价值不在于功能的堆叠,而在于如何通过形态设计打破社交壁垒,成为用户“全天佩戴…...

嵌入式学习之系统编程(九)OSI模型、TCP/IP模型、UDP协议网络相关编程(6.3)
目录 一、网络编程--OSI模型 二、网络编程--TCP/IP模型 三、网络接口 四、UDP网络相关编程及主要函数 编辑编辑 UDP的特征 socke函数 bind函数 recvfrom函数(接收函数) sendto函数(发送函数) 五、网络编程之 UDP 用…...

Java 与 MySQL 性能优化:MySQL 慢 SQL 诊断与分析方法详解
文章目录 一、开启慢查询日志,定位耗时SQL1.1 查看慢查询日志是否开启1.2 临时开启慢查询日志1.3 永久开启慢查询日志1.4 分析慢查询日志 二、使用EXPLAIN分析SQL执行计划2.1 EXPLAIN的基本使用2.2 EXPLAIN分析案例2.3 根据EXPLAIN结果优化SQL 三、使用SHOW PROFILE…...

Tauri2学习笔记
教程地址:https://www.bilibili.com/video/BV1Ca411N7mF?spm_id_from333.788.player.switch&vd_source707ec8983cc32e6e065d5496a7f79ee6 官方指引:https://tauri.app/zh-cn/start/ 目前Tauri2的教程视频不多,我按照Tauri1的教程来学习&…...
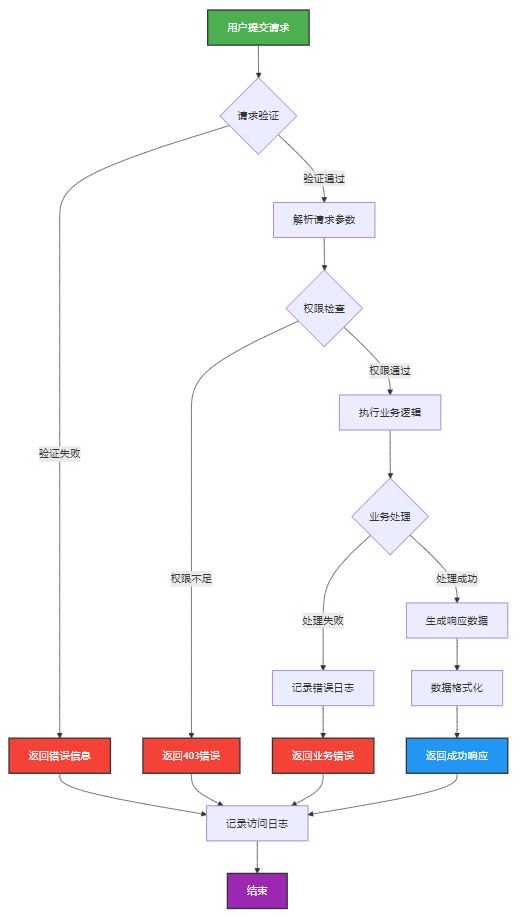
如何做好一份技术文档?从规划到实践的完整指南
如何做好一份技术文档?从规划到实践的完整指南 🌟 嗨,我是IRpickstars! 🌌 总有一行代码,能点亮万千星辰。 🔍 在技术的宇宙中,我愿做永不停歇的探索者。 ✨ 用代码丈量世界&…...

aurora与pcie的数据高速传输
设备:zynq7100; 开发环境:window; vivado版本:2021.1; 引言 之前在前面两章已经介绍了aurora读写DDR,xdma读写ddr实验。这次我们做一个大工程,pc通过pcie传输给fpga,fpga再通过aur…...
