当前位置：首页 > news >正文

【leetcode--同构字符串】

news 2026/2/9 21:29:30

要求：判断两个字符串的形式是不是一致，即是不是AABC或者ABBBCC这种。

trick：使用set（）结合zip（）。

set（）用法：用于创建一个不包含重复元素的集合

zip（）用法：用于将可迭代的对象作为参数，将对象中的元素打包成一个个元组，然后返回这些元组组成的对象。

s="abc"
t="xyz"
zipped = zip(s,t)
list_1 = list(zipped)
print(list_1) #输出[('a','x'),('b','y'),('c','z')]

解题答案：

class Solution(object):def isIsomorphic(self, s, t):return len(set(s)) == len(set(t)) == len(set(zip(s,t)))

【leetcode--同构字符串】

要求：判断两个字符串的形式是不是一致，即是不是AABC或者ABBBCC这种。 trick：使用set（）结合zip（）。 set（）用法：用于创建一个不包含重复元素的集合 zip&#…...

编程日记 2024/6/23 5:30:15

shell expr功能详解

expr命令可以实现数值运算、数值或字符串比较、字符串匹配、字符串提取、字符串长度计算等功能。它还具个特殊功能，判断变量或参数是否为整数、是否为空、是否为0等。 1.字符串表达式 ------------------------- expr支持模式匹配和字符串操作。字符串表达式的优先…...

编程日记 2024/6/23 5:28:13

java继承Thead类和实现Runnable接口创建线程的区别

一、继承Thread类创建多线程 public class Demo{public static void main(String[] args) {MyThread thread new MyThread();thread.start();}} class MyThread extends Thread{Overridepublic void run() {//子线程执行的操作} }注意：开启子线程要调用start()方法…...

编程日记 2024/6/23 5:27:11

interface Ref＜T = any＞这是什么写法?为什么写接口还需要加上＜T = any＞

问: export interface Ref<T any> { value: T [RefSymbol]: true } 这里既然是interface接口,为什么还有<T any>这是什么意思? 回答: <T any> 中的 <T> 表示这是一个泛型参数，它可以在接口中作为类型的占位符，在实际…...

编程日记 2024/6/23 5:26:10

深入探索 MongoDB GridFS：高效大文件存储与管理的全面指南

GridFS 是 MongoDB 的一个规范，用于存储和检索超过 BSON 文档大小限制（16MB）的文件。与传统的文件系统不同，GridFS 可以将一个大文件分割成多个小块，并存储在 MongoDB 的两个集合中：fs.files 和 fs.chunks。…...

编程日记 2024/6/23 5:25:08

基于CentOS Stream 9平台安装/卸载 Redis7.0.15

已更正systemctl管理Redis服务问题 1. 官方下载地址 https://redis.io/downloads/#redis-downloads 1.1 下载或上传到/opt/coisini目录下： mkdir /opt/coisini cd /opt/coisini wget https://download.redis.io/releases/redis-7.0.15.tar.gz2. 解压 tar -zxvf re…...

编程日记 2024/6/23 5:23:06

激励-保健理论和公平理论

激励-保健理论 herzberg的激励-保健理论中，保健因素是context of a job，激励因素是content of a job。 context of a job是受组织控制的因素，比如工作条件，基本工资，公司政策等，个人无法支配。content of…...

编程日记 2024/6/23 5:21:02

深入探索 Spring Boot 自定义启动画面

目录引言什么是 Spring Boot 启动画面Spring Boot 默认启动画面为什么要自定义启动画面如何自定义 Spring Boot 启动画面修改配置文件使用 Banner 接口通过图片实现启动画面ASCII 艺术画的应用进阶：基于环境变量的动态 Banner多模块项目中的启动画面Spring Boot…...

编程日记 2024/6/23 5:20:00

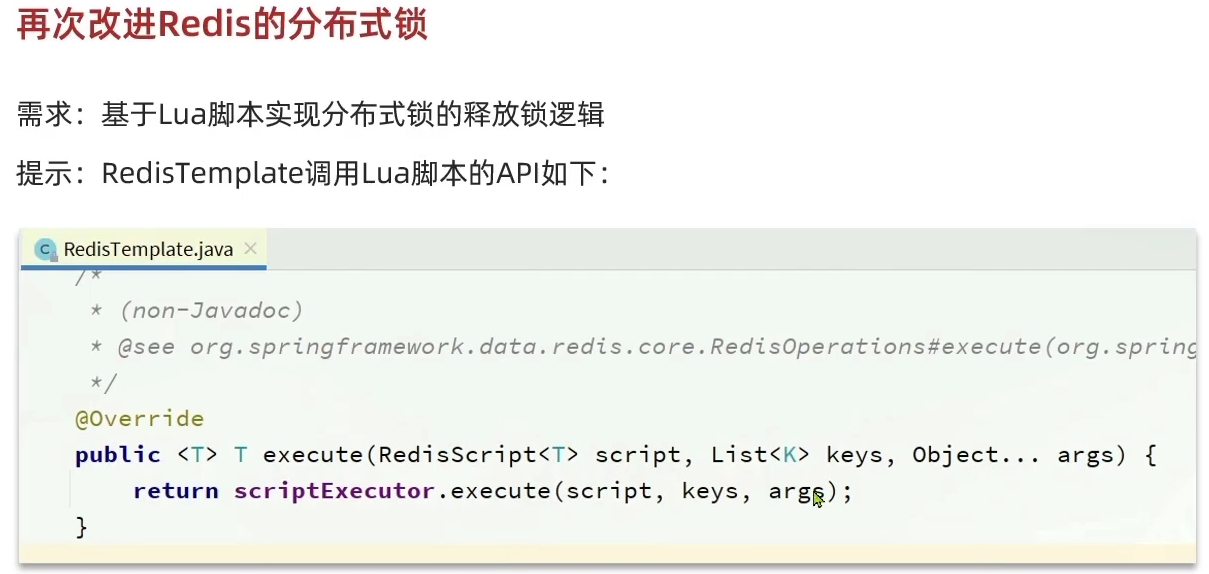
Redis实战—Redis分布式锁

本博客为个人学习笔记，学习网站与详细见：黑马程序员Redis入门到实战 P56 - P63 目录分布式锁介绍基于Redis的分布式锁 Redis锁代码实现修改业务代码分布式锁误删问题分布式锁原子性问题 Lua脚本编写脚本代码优化总结分布式锁介绍…...

编程日记 2024/6/23 5:17:58

联想Y7000P 2023款拆机教程及升级内存教程

0.电脑参数介绍联想Y7000P 2023电脑，笔者电脑CPU为i7-13700H，14核20线程；标配内存为三星的DDR5-5600MHz-8GB*2，由于电脑CPU限制，实际内存跑的频率为5200MHz; 2个内存插槽，2个固态硬盘插槽。每个内存插槽最…...

编程日记 2024/6/23 5:16:56

开发常用依赖

目录代理对象 Swagger Web 单元测试 MybatisPlus Lombok Mysql SpringBoot Jdk SpringCloud 数据库驱动包 hutool工具配置仓库通用库 maven插件 nacos注册中心 OpenFeign Spring AMQP JSON转换器 Redis 邮箱验证 Redisson分布式锁客户端代理对象 &l…...

编程日记 2024/6/23 5:12:53

【区分vue2和vue3下的element UI Empty 空状态组件，分别详细介绍属性，事件，方法如何使用，并举例】

在 Element UI（为 Vue 2 设计）和 Element Plus（为 Vue 3 设计）中，Empty（空状态）组件通常用于在数据为空或没有内容时向用户展示一种占位提示。然而，需要注意的是，Element…...

编程日记 2024/6/23 5:11:50

【AI作曲】毁掉音乐？早该来了！一个网易音乐人对于 AI 大模型音乐创作的思辨

引言：AI在创造还是毁掉音乐？ 正如当初 midjourney 和 StableDiffusion 在绘画圈掀起的风波一样，suno 和各大音乐大模型的来临，其实早该来了。 AI 在毁掉绘画？或者毁掉音乐？ 没错，但也错了。…...

编程日记 2024/6/23 5:10:49

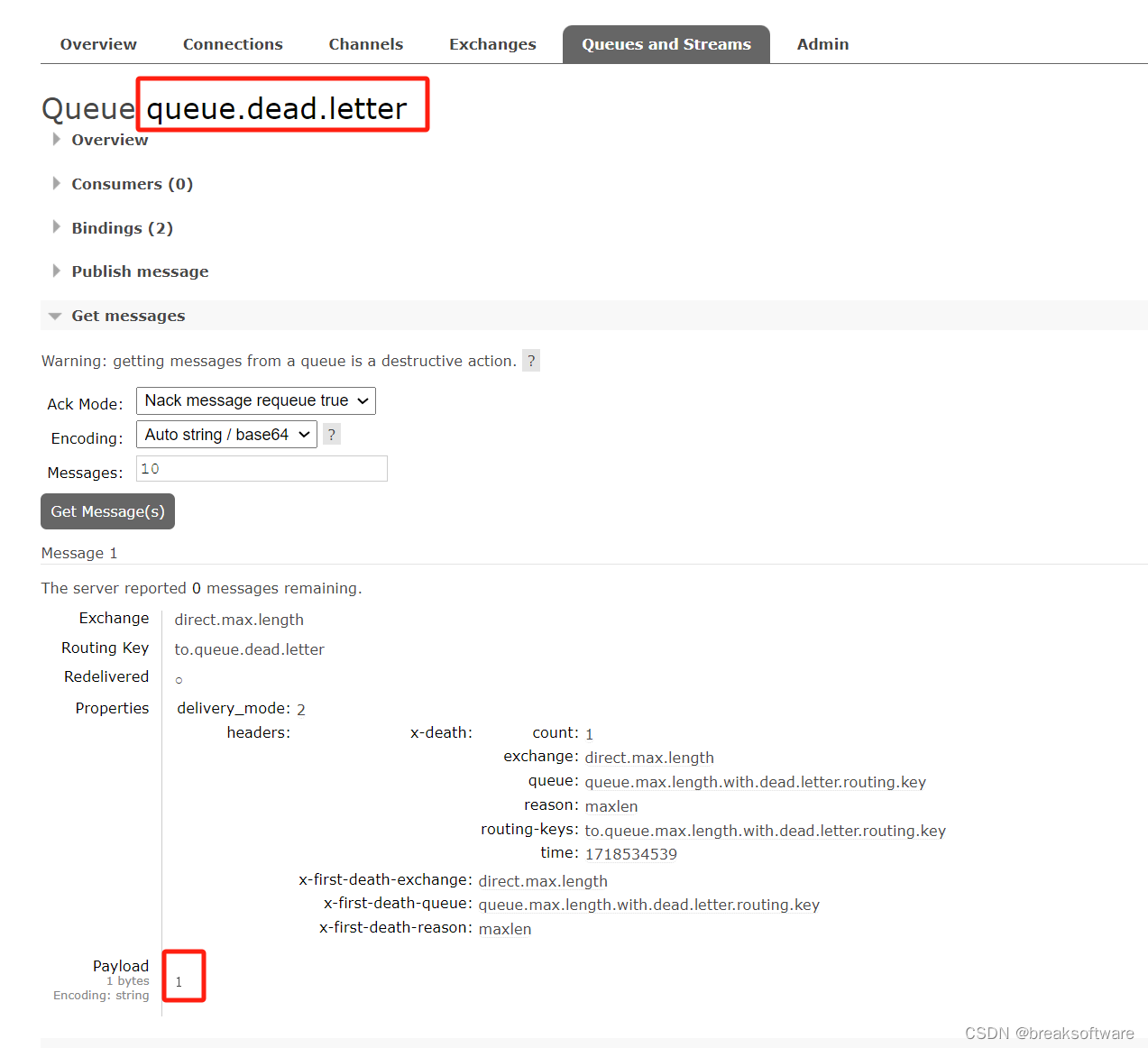
RabbitMQ实践——最大长度队列

大纲抛弃消息创建最大长度队列绑定实验转存死信创建死信队列创建可重写Routing key的最大长度队列创建绑定关系实验在一些业务场景中，我们只需要保存最近的若干条消息，这个时候我们就可以使用“最大长度队列”来满足这个需求。该队列在收到消息后&…...

编程日记 2024/6/23 5:09:47

【pytorch02】手写数字问题引入

1.数据集现实生活中遇到的问题车牌识别身份证号码识别快递单的识别都会涉及到数字识别 MNIST（收集了很多人手写的0到9数字的图片） 每个数字拥有7000个图像train/test splitting:60k vs 10k 图片大小28 28 数据集划分成训练集和测试集合的意义…...

编程日记 2024/6/23 5:08:46

【查看显卡信息】——Ubuntu和windows

1、VMware虚拟机 VMware虚拟机上不能使用CUDA/CUDNN，也安装不了显卡驱动查看显卡信息： lspci | grep -i vga 不会显示显卡信息，只会输出VMware SVGA II Adapter，表示这是一个虚拟机，无法安装和使用显卡驱动使用上…...

编程日记 2024/6/23 5:06:43

在 RK3568 上构建 Android 11 模块：深入解析 m、mm、mmm 编译命令

目录 Android 编译系统概述编译命令简介环境准备使用 m、mm、mmm 编译模块编译整个源码树编译单个模块编译指定目录下的模块高级应用并行编译清理编译结果编译特定配置在 Android 开发中，特别是在 RK3568 这样的高性能平台上，有效地编译和管理模块是确…...

编程日记 2024/6/23 5:05:41

实战｜YOLOv10 自定义目标检测

引言 YOLOv10[1] 概述和使用自定义数据训练模型概述由清华大学的研究团队基于 Ultralytics Python 包研发的 YOLOv10，通过优化模型结构并去除非极大值抑制（NMS）环节，提出了一种创新的实时目标检测技术。这些改进不仅实现了行业领…...

编程日记 2024/6/23 5:04:40

TTS前端原理学习 chatgpt生成答案

第一篇文章学习小绿鲸阅读器通篇使用chatgpt生成答案文章： https://arxiv.org/pdf/2012.15404 1. 文章概述本文提出了一种基于Distilled BERT模型的统一普通话文本到语音前端模块。该模型通过预训练的中文BERT作为文本编码器，并采用多任务学习技术…...

编程日记 2024/6/23 5:03:39

AI“音乐创作”横行给音乐家带来哪些隐忧

近日，200多名国际乐坛知名音乐人联署公开信，呼吁AI开发者、科技公司、平台和数字音乐服务商停止使用人工智能(AI)来侵犯并贬低人类艺术家的权利，具体诉求包括，停止使用AI侵犯及贬低人类艺术家的权利，要求…...

编程日记 2024/6/23 5:01:37

HTML 语义化

目录 HTML 语义化HTML5 新特性HTML 语义化的好处语义化标签的使用场景最佳实践 HTML 语义化 HTML5 新特性标准答案： 语义化标签： <header>：页头<nav>：导航<main>：主要内容<article>&#x…...

编程新知 2026/1/15 21:24:41

从零实现富文本编辑器#5-编辑器选区模型的状态结构表达

先前我们总结了浏览器选区模型的交互策略，并且实现了基本的选区操作，还调研了自绘选区的实现。那么相对的，我们还需要设计编辑器的选区表达，也可以称为模型选区。编辑器中应用变更时的操作范围，就是以模型选区为基准来…...

编程新知 2026/1/16 16:34:26

《通信之道——从微积分到 5G》读书总结

第1章绪论 1.1 这是一本什么样的书通信技术，说到底就是数学。那些最基础、最本质的部分。 1.2 什么是通信通信发送方接收方承载信息的信号解调出其中承载的信息信息在发送方那里被加工成信号（调制） 把信息从信号中抽取出来&am…...

编程新知 2026/2/7 11:01:56

Unit 1 深度强化学习简介

Deep RL Course ——Unit 1 Introduction 从理论和实践层面深入学习深度强化学习。学会使用知名的深度强化学习库，例如 Stable Baselines3、RL Baselines3 Zoo、Sample Factory 和 CleanRL。在独特的环境中训练智能体，比如 SnowballFight、Huggy the Do…...

编程新知 2026/2/8 12:54:53

分布式增量爬虫实现方案

之前我们在讨论的是分布式爬虫如何实现增量爬取。增量爬虫的目标是只爬取新产生或发生变化的页面，避免重复抓取，以节省资源和时间。在分布式环境下，增量爬虫的实现需要考虑多个爬虫节点之间的协调和去重。另一种思路：将增量判…...

编程新知 2026/2/6 1:18:56

Device Mapper 机制

Device Mapper 机制详解 Device Mapper（简称 DM）是 Linux 内核中的一套通用块设备映射框架，为 LVM、加密磁盘、RAID 等提供底层支持。本文将详细介绍 Device Mapper 的原理、实现、内核配置、常用工具、操作测试流程，并配以详细的…...

编程新知 2025/12/14 13:11:33

以光量子为例，详解量子获取方式

光量子技术获取量子比特可在室温下进行。该方式有望通过与名为硅光子学（silicon photonics）的光波导（optical waveguide）芯片制造技术和光纤等光通信技术相结合来实现量子计算机。量子力学中，光既是波又是粒子。光子本…...

编程新知 2026/2/7 11:51:32

MySQL JOIN 表过多的优化思路

当 MySQL 查询涉及大量表 JOIN 时，性能会显著下降。以下是优化思路和简易实现方法： 一、核心优化思路减少 JOIN 数量数据冗余：添加必要的冗余字段（如订单表直接存储用户名）合并表：将频繁关联的小表合并成…...

编程新知 2026/1/11 6:22:16

鸿蒙（HarmonyOS5）实现跳一跳小游戏

下面我将介绍如何使用鸿蒙的ArkUI框架，实现一个简单的跳一跳小游戏。 1. 项目结构 src/main/ets/ ├── MainAbility │ ├── pages │ │ ├── Index.ets // 主页面 │ │ └── GamePage.ets // 游戏页面 │ └── model │ …...

编程新知 2025/11/20 18:21:59

VisualXML全新升级 | 新增数据库编辑功能

VisualXML是一个功能强大的网络总线设计工具，专注于简化汽车电子系统中复杂的网络数据设计操作。它支持多种主流总线网络格式的数据编辑（如DBC、LDF、ARXML、HEX等），并能够基于Excel表格的方式生成和转换多种数据库文件。由此&…...

编程新知 2026/2/6 5:51:15

相关文章：