公式推导+dfs简版
写在前面的话:心可以冷,但手不能停
第一题:C. Flexible String
题目大意:给一个aaa字符串和bbb字符串和数字kkk,首先设置一个计数器cntcntcnt,其中可以对aaa字符串做以下操作:替换aaa中的一个字母xxx,将字母xxx加入到集合QQQ,如果这个字母已经在集合QQQ中了,则cntcntcnt不动,否则cnt++cnt++cnt++,记s[l,r]s[l,r]s[l,r]为在[l,r][l,r][l,r]区间中aaa和bbb的字母全相等。达到的目标为在cnt≤kcnt \leq kcnt≤k的情况下,让s[l,r]s[l,r]s[l,r]的数量最大。
解题思路: 这个题可以这样想,对于任意一个a[i]≠b[i]a[i] \neq b[i]a[i]=b[i],可以将这个位置记作一个断点,被断点隔开的若干个区间可以用这样的形式来表达s[l,r]s[l,r]s[l,r]的数量:len∗(len+1)/2len*(len+1)/2len∗(len+1)/2,其中len为区间内的字母数量。我们注意到如果将某个满足a[i]≠b[i]a[i] \neq b[i]a[i]=b[i]的字母加入到集合QQQ中,则区间可能被连上,注意可能断点是由两个字母组成的。这样的话,考虑k最大可能为101010,则可以用数位dpdpdp或者dfsdfsdfs等,来枚举所有可能性。枚举出一种可能性,之后只要用O(n)O(n)O(n)判断即可,大概是10810^8108这样的级别,那么这里的枚举状态可以用这种形式表达:
for(int i=0;i<1024;i++)
注意,由于我把集合中的字母用mapmapmap映射,所以所有字母不能映射到000,否则wronganswerontest3wrong\space answer \space on\space test3wrong answer on test3
代码:
#include<iostream>
#include<cstdio>
#include<vector>
#include<stack>
#include<map>
using namespace std;
typedef long long ll;
const int length = 1e5 + 5;
char a[length];
char b[length];
ll max(ll a, ll b)
{if (a > b)return a;else return b;
}
ll solve(int i, map<char, int> &mp,int n,int k)
{vector<int> flag(20, 0);int q = 0;for (int j = 1; j <= 10; j++){if (i&(1 << j)){flag[j] = 1;q++;}}if(q>k)return 0;int s = 0;ll res = 0;while (s < n){int tmp = s;while (a[s] == b[s]||flag[mp[a[s]]]==1){s++;if (s >= n)break;}int len = s - tmp;res = res + (ll)(len + 1)*len / 2;s++;}return res;}
int main(void)
{int t;scanf_s("%d", &t);for (int i = 0; i < t; i++){int n;int k;scanf_s("%d%d", &n, &k);getchar();//收\nscanf_s("%s", a,sizeof(a));getchar();//收\nscanf_s("%s", b,sizeof(b));getchar();map<char,int> mp;int cnt = 0;for (int i = 0; i < n; i++){if (a[i] != b[i]){if (mp[a[i]] == 0){mp[a[i]] = ++cnt;}}}if (cnt <= k){ll tmp = (ll)n*(n + 1) / 2;printf("%lld\n", tmp);continue;}vector<ll> dp(1500, 0);ll ans = -1;for (int i = 0; i < 1024; i++){ll a=solve(i*2, mp,n,k);ans = max(ans, a);}printf("%lld\n", ans);}
}
第2题:D. Flexible String Revisit
这个题比较有意思
题目大意: 给一个由0和1组成的两个字符串,对字符串a可以做以下操作:可以任选一个数字对其进行反转,问达到两个字符串第一次相等所需要的操作次数期望。
解题思路:
参考文章
代码:
#include<iostream>
#include<cstdio>
#include<vector>
using namespace std;
typedef long long ll;
int mod = 998244353;
const int length = 1e6 + 5;
int f[length][2];
int dp[length];
char a[length];
char b[length];
int ksm(int k)
{int tmp = mod-2;int base = k;int ans = 1;while (tmp){if (tmp % 2 == 1){ans = (ll)ans*base%mod;}base = (ll)base*base%mod;tmp = tmp >> 1;}return ans;
}
int solve(int n, int k)
{f[n][0] = 1;f[n][1] = 1;for (int i = n-1; i >= 0; i--){int now = ((ll)1 - (ll)(n - i)*f[i + 1][1]%mod *ksm(n) % mod + mod) % mod;f[i][0] = ((ll)1 + (ll)(f[i+1][0])*(n-i)%mod*ksm(n) % mod) % mod*ksm(now)%mod;f[i][1] = (ll)i*ksm(n) % mod*ksm(now) % mod;}dp[0] = f[0][0];for (int i = 1; i <= k; i++){dp[i] = (ll)((ll)dp[i - 1] * f[i][1] % mod + f[i][0]) % mod;}return dp[k];
}
int main(void)
{int t;scanf_s("%d", &t);for (int i = 0; i < t; i++){int n;scanf_s("%d", &n);int k = 0;getchar();scanf_s("%s", a,sizeof(a));//a.push_back(t);getchar();scanf_s("%s", b, sizeof(b));getchar();for (int i = 0; i < n; i++){if (a[i] != b[i])k++;}int a1=solve(n, k);printf("%d\n", a1);}
}
相关文章:

公式推导+dfs简版
写在前面的话:心可以冷,但手不能停 第一题:C. Flexible String 题目大意:给一个aaa字符串和bbb字符串和数字kkk,首先设置一个计数器cntcntcnt,其中可以对aaa字符串做以下操作:替换aaa中的一个字母xxx&#…...

论文笔记 | 标准误聚类问题
关于标准误的选择,如是否选择稳健性标准误、是否采取聚类标准误。之前一直是困惑的,惯用的做法是类似主题的文献做法。所以这一次,借计量经济学课程之故,较深入学习了标准误的选择问题。 在开始之前推荐一个知乎博主。他阅读了很…...
银行管理系统--课后程序(Python程序开发案例教程-黑马程序员编著-第7章-课后作业)
实例1:银行管理系统 从早期的钱庄到现如今的银行,金融行业在不断地变革;随着科技的发展、计算机的普及,计算机技术在金融行业得到了广泛的应用。银行管理系统是一个集开户、查询、取款、存款、转账、锁定、解锁、退出等一系列的功…...
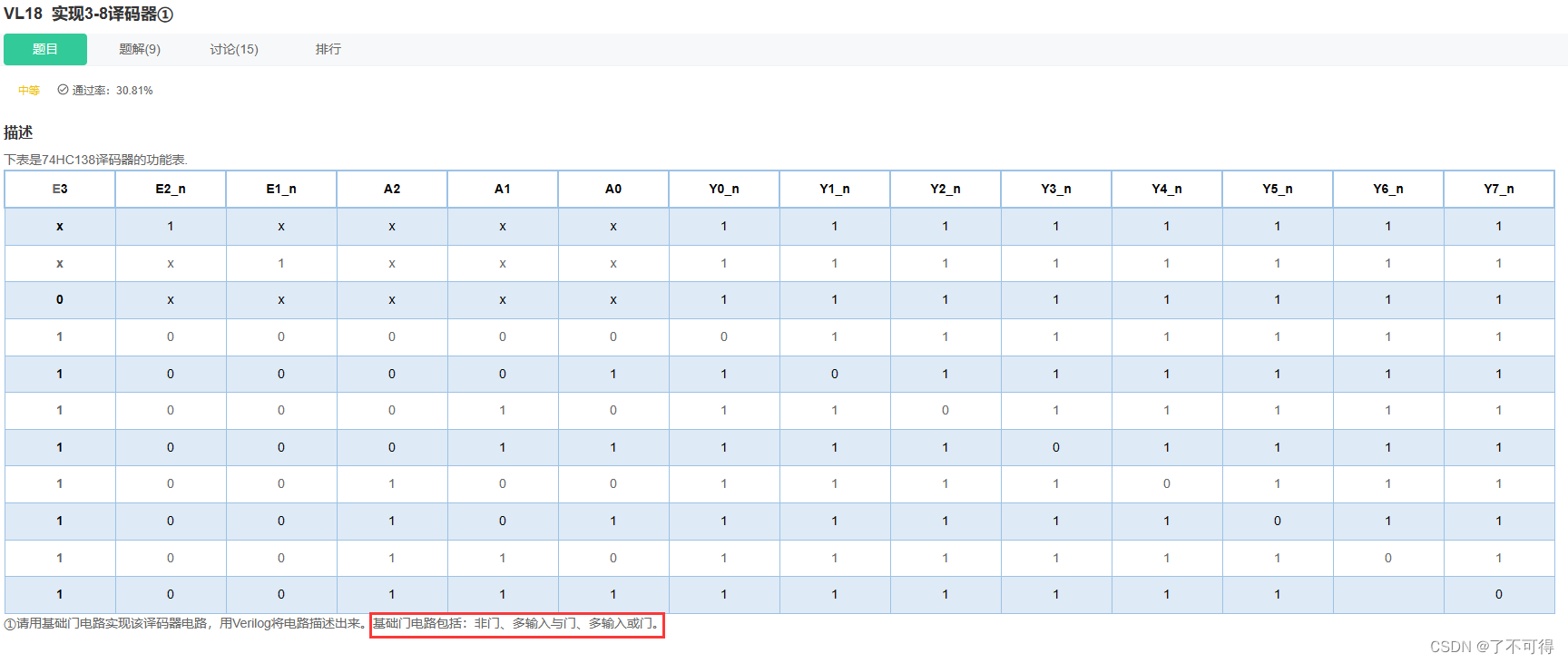
【18】组合逻辑 - VL18 实现3-8译码器①
VL18 实现3-8译码器① 1 题目 【这题我的思路非常绝境】奈斯 !! 看真值表的思路:Yi所在列【0仅一个其余全1】,故【以0为对象求解】 观察发现:E3 E2_n E1_n = 100 时 是 译码的使能信号 ; 并且E3 E2_n E1_n为其他值时,都不使能译码 然后就很简单,没有仿真就成功了 2 代…...

2020蓝桥杯真题最长递增 C语言/C++
题目描述 在数列a_1 ,a_2,⋯,a_n 中,如果a_i <a_i1 <a_i2<⋯<a_j,则称 a_i至 a_j为一段递增序列,长度为 j−i1。 定一个数列,请问数列中最长的递增序列有多长。 输入描述 输入的第一行包含一个整数 n。 第二行包含…...
| 机考必刷)
华为OD机试题 - 寻找连续区间(JavaScript)| 机考必刷
更多题库,搜索引擎搜 梦想橡皮擦华为OD 👑👑👑 更多华为OD题库,搜 梦想橡皮擦 华为OD 👑👑👑 更多华为机考题库,搜 梦想橡皮擦华为OD 👑👑👑 华为OD机试题 最近更新的博客使用说明本篇题解:寻找连续区间题目输入输出示例一输入输出说明示例二输入输出Cod…...

一次疲惫的调试--累了及时透气
原创 射频清茶 深山小老虎 2023-03-11 14:32发表于广东 收录于合集 #射频调试3个 #网分4个 #Wi-Fi 2个 进来透透气 道不尽红尘舍恋 诉不完人间恩怨 世世代代都是缘 喝着相同的水 留着相同的血 这条路漫漫又长远 红花当然配绿叶 这一辈子谁来陪 渺渺茫茫来又回 往日情景再…...
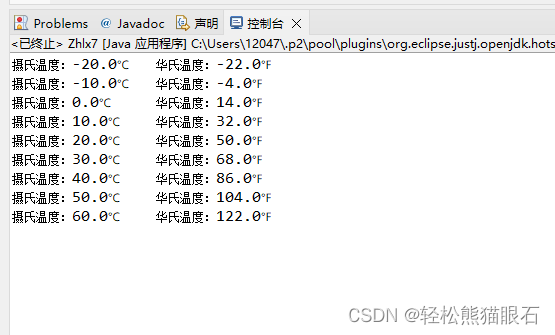
综合练习7 摄氏度转华氏温度(“\t“的使用,循环语句)
综合练习7 摄氏度转华氏温度 使用do…while循环,在控制台输入摄氏温度与华氏温度的对照表。 对照表从摄氏温度-30℃到50℃,每行间隔10℃,运行如下: 摄氏温度:-30℃ 华氏温度:-22.0℉ 摄氏温度:…...

AWS数据库总结
RDS – 联机事务处理OLTP(Online Transaction Processing),包括: SQL ServerOracleMySQL ServerPostgreSQLAuroraMariaDB非关系数据库DynamoDB数据仓库RedShift – 联机分析处理OLAP(Online Analytics Processing&…...
2个步骤就能批量给视频添加滚动字幕
现在很多小伙伴在剪辑视频的时候都会给自己的视频添加适配的字幕,但是有很多的视频想要添加一样的滚动字幕时,有一个能批量添加剪辑的工具非常重要,今天小编就给大家分享一个可以批量剪辑大量视频的工具,下面一起看看具体的操作步…...
PHP 的运行方式有哪些?
PHP本质上的运行方式可以分为两种: 基于命令行的基于PHP-FPM的 但实际上,PHP能做的事很多,很多场景下,不同的运行方式能让开发更方便,减轻各种工作。 测试开发 PHP内置了一个HTTP 的server。这意味着,很…...

Web学习3_JavaScript
1.1 JS的调用方式与执行顺序 使用方式 HTML页面中的任意位置加上<script type"module"></script>标签即可。 常见使用方式有以下几种: 直接在<script type"module"></script>标签内写JS代码。script type"modu…...

「MySQL基础」不可重复读和幻读的区别
「MySQL基础」不可重复读和幻读的区别 文章参考: 在数据库中不可重复读和幻读到底应该怎么分? 作者:暖猫Suki、普通熊猫 文章目录「MySQL基础」不可重复读和幻读的区别一、概述二、小结一、概述 正好在琢磨这个问题,也被搞得头昏…...

CorelDRAW2023最新版新增功能200多个新模板
CorelDRAW是一款平面矢量绘图排版软件,CorelDRAW运用涵盖企业VI设计,广告设计,包装设计,画册设计,海报、招贴设计,UI界面设计,网页设计,书籍装帧设计,插画设计࿰…...

springboot自定义日志以及行号正确展示
在开发springboot项目时,我们可能需要自定义日志实现。需要对slf4j的日志实现进行一次外层包装 这个很简单,按照org.slf4j.Logger方式定义一个类Logger类MyLogger。 让后实现MyLoggerImpl: public class MyLoggerImpl implements CoreLogge…...

【GAOPS055】verilog 乘法、除法和取余
乘法硬件原理 结论 可以将乘法A x B转为A的移位相加。 利用乘2n就是左移n位的特性乘2^n就是左移n位的特性乘2n就是左移n位的特性,将数拆分为2n2^n2n表示 思路1 原始列竖式计算方法ref例2.9 思路2 B总是可以拆分为:B(an2nan−12n−1...a121a020)B(…...
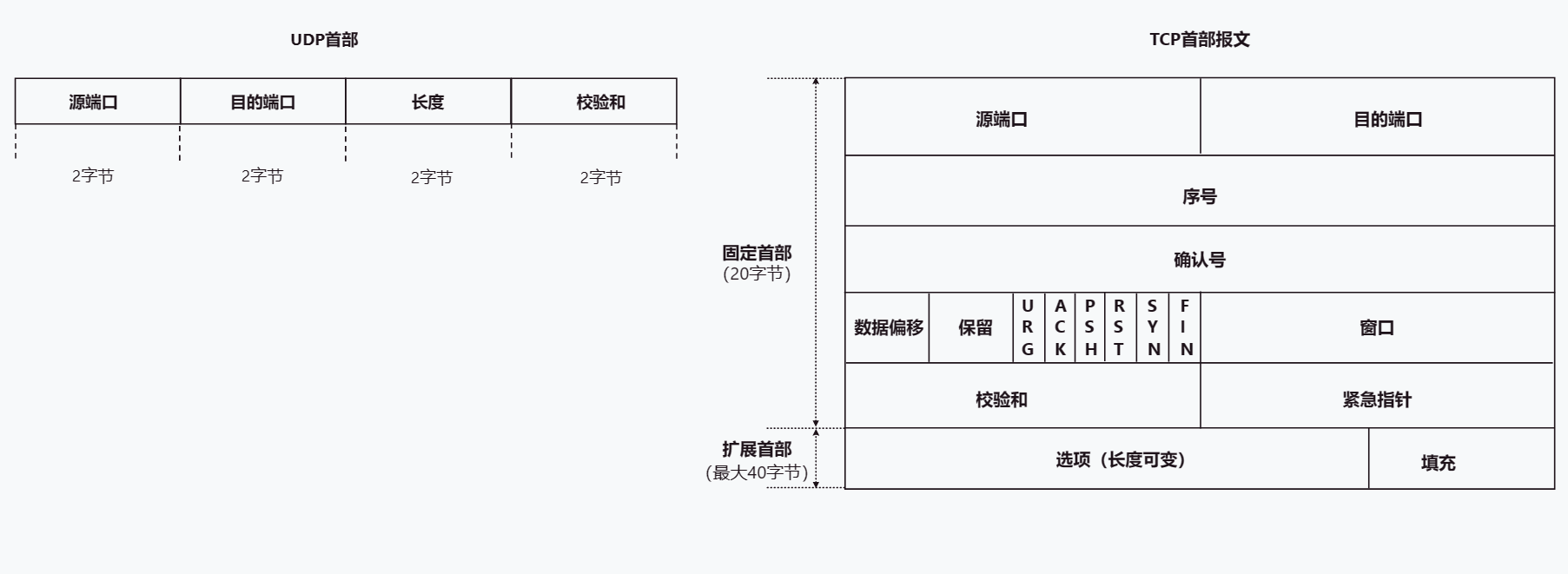
TCP UPD详解
文章目录TCP UDP协议1. 概述2. 端口号 复用 分用3. TCP3.1 TCP首部格式3.2 建立连接-三次握手3.3 释放连接-四次挥手3.4 TCP流量控制3.5 TCP拥塞控制3.6 TCP可靠传输的实现3.7 TCP超时重传4. UDP5.TCP与UDP的区别TCP UDP协议 1. 概述 TCP、UDP协议是TCP/IP体系结构传输层中的…...

金三银四、金九银十 面试宝典 MySQL面试题 超级无敌全的面试题汇总(超万字的面试题,让你的MySQL无可挑剔)
MySQL数据库 - 面试宝典 又到了 金三银四、金九银十 的时候了,是时候收藏一波面试题了,面试题可以不学,但不能没有!🥁🥁🥁 一个合格的 计算机打工人 ,收藏夹里必须有一份 MySQL 八…...

【Java】初识Java
Java和C语言有许多类似之处,这里就只挑不一样的点来说,所以会比较杂乱哈~ 目录 1.数据类型 2.输入与输出 2.1三种输出 2.2输入 2.3循环输入输出 //猜数字小游戏 //打印乘法口诀表 3.方法 //交换两个数(数组的应用) //模…...

JVM相关知识
JVM类加载过程类什么时候被加载什么情况下会发生栈内存溢出JVM内存模型常量池回收方法区垃圾回收流程圾收集算法分代收集理论标记-清除算法标记-复制算法标记-整理算法类加载过程 加载–验证–准备–解析–初始化–使用–卸载 加载:通过全类名获取类的二进制流…...

【网络】每天掌握一个Linux命令 - iftop
在Linux系统中,iftop是网络管理的得力助手,能实时监控网络流量、连接情况等,帮助排查网络异常。接下来从多方面详细介绍它。 目录 【网络】每天掌握一个Linux命令 - iftop工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景…...

盘古信息PCB行业解决方案:以全域场景重构,激活智造新未来
一、破局:PCB行业的时代之问 在数字经济蓬勃发展的浪潮中,PCB(印制电路板)作为 “电子产品之母”,其重要性愈发凸显。随着 5G、人工智能等新兴技术的加速渗透,PCB行业面临着前所未有的挑战与机遇。产品迭代…...

Linux云原生安全:零信任架构与机密计算
Linux云原生安全:零信任架构与机密计算 构建坚不可摧的云原生防御体系 引言:云原生安全的范式革命 随着云原生技术的普及,安全边界正在从传统的网络边界向工作负载内部转移。Gartner预测,到2025年,零信任架构将成为超…...

mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包
文章目录 现象:mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包遇到 rpm 命令找不到已经安装的 MySQL 包时,可能是因为以下几个原因:1.MySQL 不是通过 RPM 包安装的2.RPM 数据库损坏3.使用了不同的包名或路径4.使用其他包…...
中的KV缓存压缩与动态稀疏注意力机制设计)
大语言模型(LLM)中的KV缓存压缩与动态稀疏注意力机制设计
随着大语言模型(LLM)参数规模的增长,推理阶段的内存占用和计算复杂度成为核心挑战。传统注意力机制的计算复杂度随序列长度呈二次方增长,而KV缓存的内存消耗可能高达数十GB(例如Llama2-7B处理100K token时需50GB内存&a…...

sipsak:SIP瑞士军刀!全参数详细教程!Kali Linux教程!
简介 sipsak 是一个面向会话初始协议 (SIP) 应用程序开发人员和管理员的小型命令行工具。它可以用于对 SIP 应用程序和设备进行一些简单的测试。 sipsak 是一款 SIP 压力和诊断实用程序。它通过 sip-uri 向服务器发送 SIP 请求,并检查收到的响应。它以以下模式之一…...

JVM虚拟机:内存结构、垃圾回收、性能优化
1、JVM虚拟机的简介 Java 虚拟机(Java Virtual Machine 简称:JVM)是运行所有 Java 程序的抽象计算机,是 Java 语言的运行环境,实现了 Java 程序的跨平台特性。JVM 屏蔽了与具体操作系统平台相关的信息,使得 Java 程序只需生成在 JVM 上运行的目标代码(字节码),就可以…...

推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材)
推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材) 这个项目能干嘛? 使用 gemini 2.0 的 api 和 google 其他的 api 来做衍生处理 简化和优化了文生图和图生图的行为(我的最主要) 并且有一些目标检测和切割(我用不到) 视频和 imagefx 因为没 a…...

c# 局部函数 定义、功能与示例
C# 局部函数:定义、功能与示例 1. 定义与功能 局部函数(Local Function)是嵌套在另一个方法内部的私有方法,仅在包含它的方法内可见。 • 作用:封装仅用于当前方法的逻辑,避免污染类作用域,提升…...

前端开发者常用网站
Can I use网站:一个查询网页技术兼容性的网站 一个查询网页技术兼容性的网站Can I use:Can I use... Support tables for HTML5, CSS3, etc (查询浏览器对HTML5的支持情况) 权威网站:MDN JavaScript权威网站:JavaScript | MDN...
