LeetCode.51N皇后详解
问题描述
按照国际象棋的规则,皇后可以攻击与之处在同一行或同一列或同一斜线上的棋子。
n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上,并且使皇后彼此之间不能相互攻击。
给你一个整数 n ,返回所有不同的 n 皇后问题 的解决方案。
每一种解法包含一个不同的 n 皇后问题 的棋子放置方案,该方案中 'Q' 和 '.' 分别代表了皇后和空位。
n 皇后问题是一个经典的回溯算法问题,其目标是在一个 n×n 的棋盘上放置 n 个皇后,使得这些皇后不能相互攻击。这意味着任何两个皇后不能处在同一行、同一列或同一斜线上。这个问题不仅是计算机科学中的一个重要问题,也是数学和人工智能领域的研究对象,涉及到组合数学、图论、算法设计等多个领域。
解题思路
回溯法的应用
n 皇后问题的核心解法是回溯算法,这是一种通过试错来寻找问题解决方法的算法。当它通过尝试可能的分步解决方案后发现当前解决方案不可能成立(即不能满足问题的约束条件),它会取消上一步甚至是几步的计算,再通过其他的可能的分步解决方案继续尝试。
检查冲突
在 n 皇后问题中,核心的挑战是如何有效地检查“攻击”(冲突)情况。这通常涉及以下检查:
- 列冲突:确保在同一列不放置多于一个皇后。
- 行冲突:通常通过算法的设计(一行只放置一个皇后)自然避免。
- 对角线冲突:需要检查两种对角线——从左上到右下和从左下到右上。这可以通过计算线性方程来实现,例如使用对角线的索引差和和来标识每条对角线。
数据结构的选择
使用数组来追踪哪些位置是被攻击状态是解决问题的关键:
- 列标记:使用一个大小为
n的数组来标记哪些列已被占用。 - 对角线标记:使用两个大小为
2n-1的数组来标记两组对角线的占用情况。对于每个皇后在(r, c)的位置,它会占用第c列,第r+c的"/"方向对角线和第r-c+n-1的"\"方向对角线。
代码示例
class Solution {
public:std::vector<std::vector<std::string>> solveNQueens(int n) {std::vector<std::vector<std::string>> solutions;std::vector<std::string> board(n, std::string(n, '.'));std::vector<int> cols(n, 0), diag1(2 * n - 1, 0), diag2(2 * n - 1, 0);backtrack(solutions, board, cols, diag1, diag2, 0, n);return solutions;}private:void backtrack(std::vector<std::vector<std::string>>& solutions,std::vector<std::string>& board, std::vector<int>& cols,std::vector<int>& diag1, std::vector<int>& diag2, int row,int n) {if (row == n) {solutions.push_back(board);return;}for (int col = 0; col < n; col++) {if (cols[col] || diag1[row + col] || diag2[row - col + n - 1]) {continue;}board[row][col] = 'Q';cols[col] = diag1[row + col] = diag2[row - col + n - 1] = 1;backtrack(solutions, board, cols, diag1, diag2, row + 1, n);board[row][col] = '.';cols[col] = diag1[row + col] = diag2[row - col + n - 1] = 0;}}
};扩展
组合数学
n 皇后问题是组合数学的一个实例,特别是在它涉及到排列和组合的计算上。每种有效的解决方案实际上是对 n 个数字的一个排列,每个数字代表皇后在特定行的列位置。
复杂度分析
虽然回溯算法在理论上是一种暴力搜索方法,它的时间复杂度在最坏情况下是指数级的,但通过有效的剪枝,实际的运行时间可以大大减少。这种算法通常是用于解决复杂度较高、解空间庞大的问题。
图论的视角
从图论的角度看,n 皇后问题可以被看作是在 n×n 的图中找到一个安全的顶点集合,其中任意两个顶点都不是相互可达的。这种图的特殊构造使其成为图着色问题的一个变种。
相关文章:

LeetCode.51N皇后详解
问题描述 按照国际象棋的规则,皇后可以攻击与之处在同一行或同一列或同一斜线上的棋子。 n 皇后问题 研究的是如何将 n 个皇后放置在 nn 的棋盘上,并且使皇后彼此之间不能相互攻击。 给你一个整数 n ,返回所有不同的 n 皇后问题 的解决方案…...

计算机网络之奇偶校验码和CRC冗余校验码
今天我们来看看有关于计算机网络的知识——奇偶校验码和CRC冗余校验码,这两种检测编码的方式相信大家在计算机组成原理当中也有所耳闻,所以今天我就来跟大家分享有关他们的知识。 奇偶校验码 奇偶校验码是通过增加冗余位使得码字中1的个数恒为奇数或偶数…...
二叉树经典OJ练习
个人主页:C忠实粉丝 欢迎 点赞👍 收藏✨ 留言✉ 加关注💓本文由 C忠实粉丝 原创 二叉树经典OJ练习 收录于专栏【数据结构初阶】 本专栏旨在分享学习数据结构学习的一点学习笔记,欢迎大家在评论区交流讨论💌 目录 前置说…...

【OpenHarmony4.1 之 U-Boot 2024.07源码深度解析】008 - make distclean 命令解析
【OpenHarmony4.1 之 U-Boot 2024.07源码深度解析】008 - make distclean 命令解析 一、make V=1 distclean 命令解析系列文章汇总:《【OpenHarmony4.1 之 U-Boot 源码深度解析】000 - 文章链接汇总》 本文链接:《【OpenHarmony4.1 之 U-Boot 2024.07源码深度解析】008 - mak…...
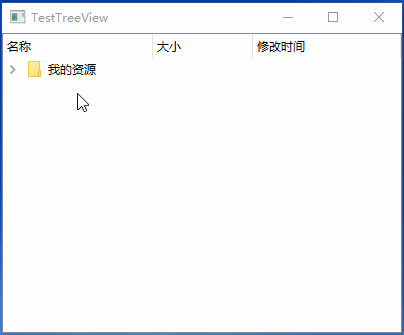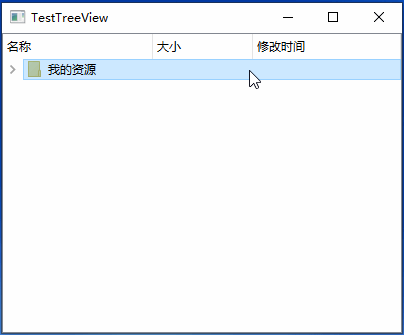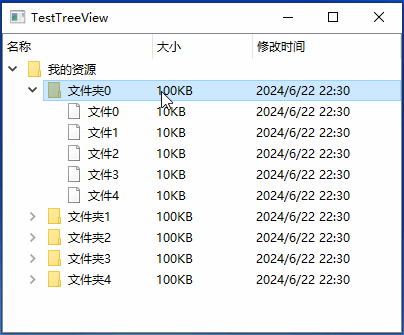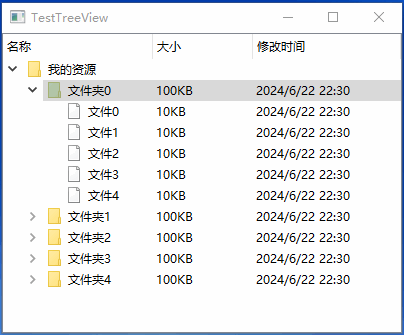
QTreeView双击任意列展开
一.效果 二.原理 重点是如何通过其他列的QModelIndex(假设为index),获取第一列的QModelIndex(假设为firstColumnIndex)。代码如下所示: QModelIndex firstColumnIndex = model->index(index.row(), 0, index.parent()); 这里要注意index函数的第三个参数,第三个参…...
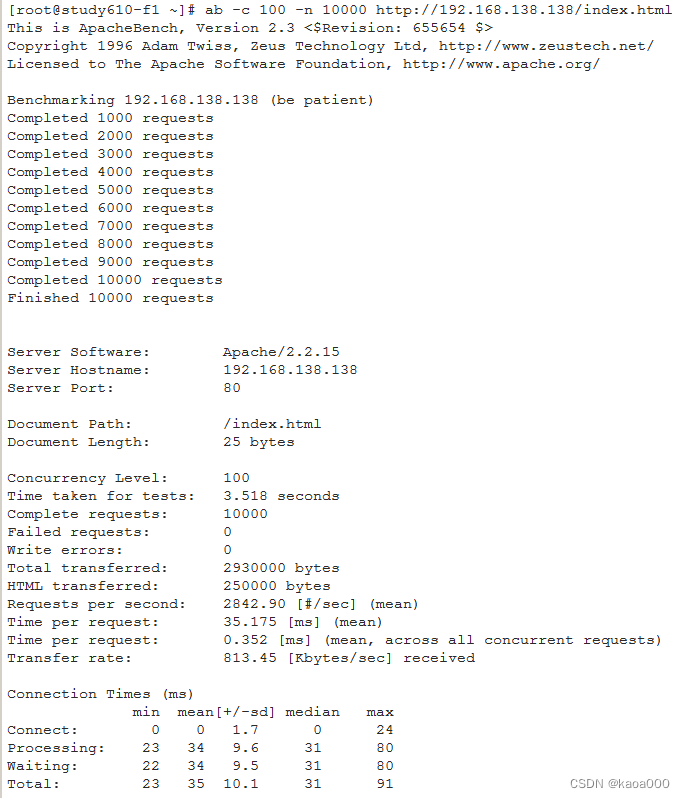
Linux入门攻坚——26、Web Service基础知识与httpd配置-2
http协议 URL:Uniform Resource Locator,统一资源定位符 URL方案:scheme,如http://,https:// 服务器地址:IP:port 资源路径: 示例:http://www.test.com:80/bbs/…...

相由心生与事出反常必有妖
从端午节之日生病起,已就医三次,快半个月了。医检的结论是老病复发—— 上呼吸道感染 。原本并无大碍,加之“水不在深,有龙则灵”的张龙医生处方得当,现已病情好转。只是“800727”趁人之危,兴灾乐祸地欲从…...

微信小程序---支付
一、判断是否登录 如果没有登录,走前端登录流程,不再赘述 二、获取订单编号 跟自己的后端商议入参,然后获取订单编号 三、通过订单编号获取wx.requestPayment()需要的参数 获取订单编号再次请求后端接口,拿到wx.requestPayme…...
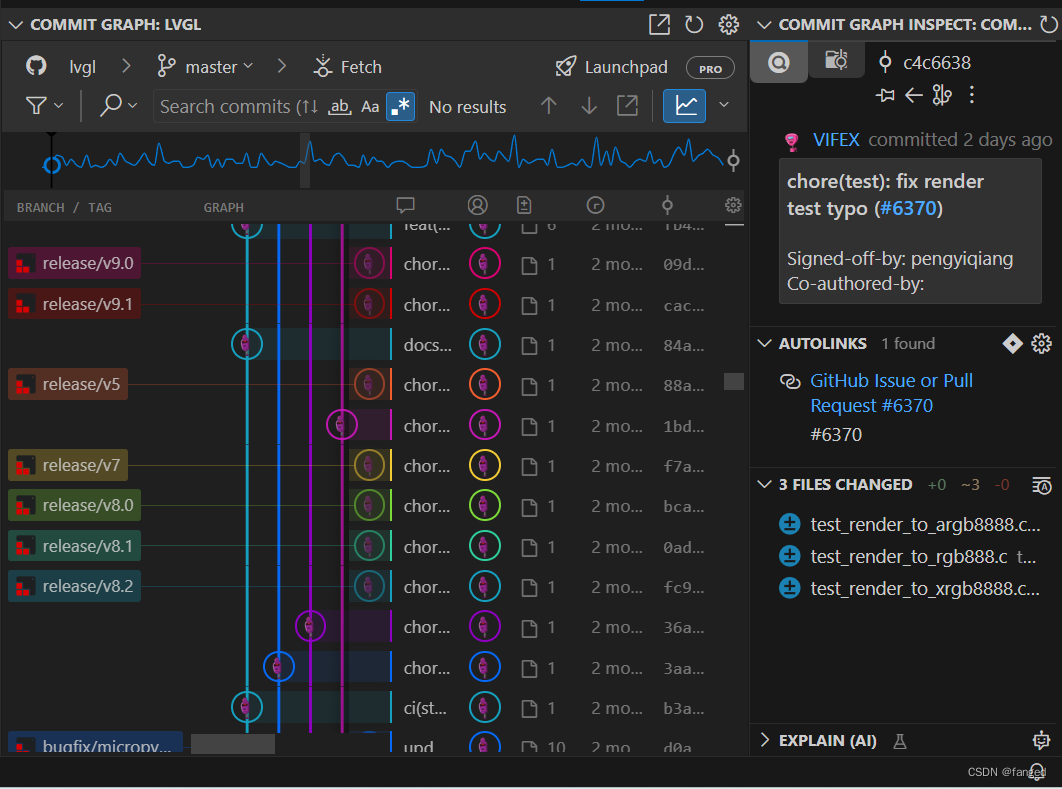
Git学习2 -- VSCode中的Git
看了下,主要的插件有3个。自带的Source Control。第1个是Gitlens,第2个是Git Graph。第三个还有个git history。 首先是Source Control。界面大概是这样的。 还是挺直观的。在第一栏source control,可以进行基本的git操作。主要的git操作都是…...

VC++支持断点续下或续传的功能
VC使用多线程和Socket实现断点续下 一、断点续下的基本原理: 1.断点续传的理解可以分为两部分:一部分是断点,一部分是续传。断点的由来是在下载过程中,将一个下载文件分成了多个部分,同时进行多个部分一起的下载&…...
机器学习数学原理专题——线性分类模型:损失函数推导新视角——交叉熵
目录 二、从回归到线性分类模型:分类 3.分类模型损失函数推导——极大似然估计法 (1)二分类损失函数——极大似然估计 (2)多分类损失函数——极大似然估计 4.模型损失函数推导新视角——交叉熵 (1&#x…...

windows和linux路径斜杆转换脚本,打开即用
前言: windows和linux的目录路径斜杆是相反的,在ssh或者其他什么工具在win和ubuntu传文件时候经常需要用到两边的路径,有这个工具就不用手动去修改斜杆反斜杠了。之前有个在线网站,后来挂了,就想着自己搞一个脚本来用。…...

在Android系统中,查看apk安装路径
在Android系统中,应用通常安装在内部存储的特定目录下。要找到已安装应用的路径,可以通过ADB(Android Debug Bridge)工具来查询。以下是一些步骤和命令,可以帮助你找到应用的安装路径: 使用pm list package…...

管理不到位,活该执行力差?狠抓这4点要素,强化执行力
管理不到位,活该执行力差?狠抓这4点要素,强化执行力 一:强化制度管理 1、权责分明,追责管理 要知道,规章制度其实就是一种“契约”。 在制定制度和规则的时候,民主一点,征求团队成员…...

应届毕业之本科简历制作
因为毕设以及编制岗位面试,最近好久没有更新了,刚好有同学问如何制作简历,我就准备将我自己制作简历的流程分享给各位,到此也算是一个小的结束,拿了工科学位证书毕业去做🐂🐎了。 简历主要包含内…...
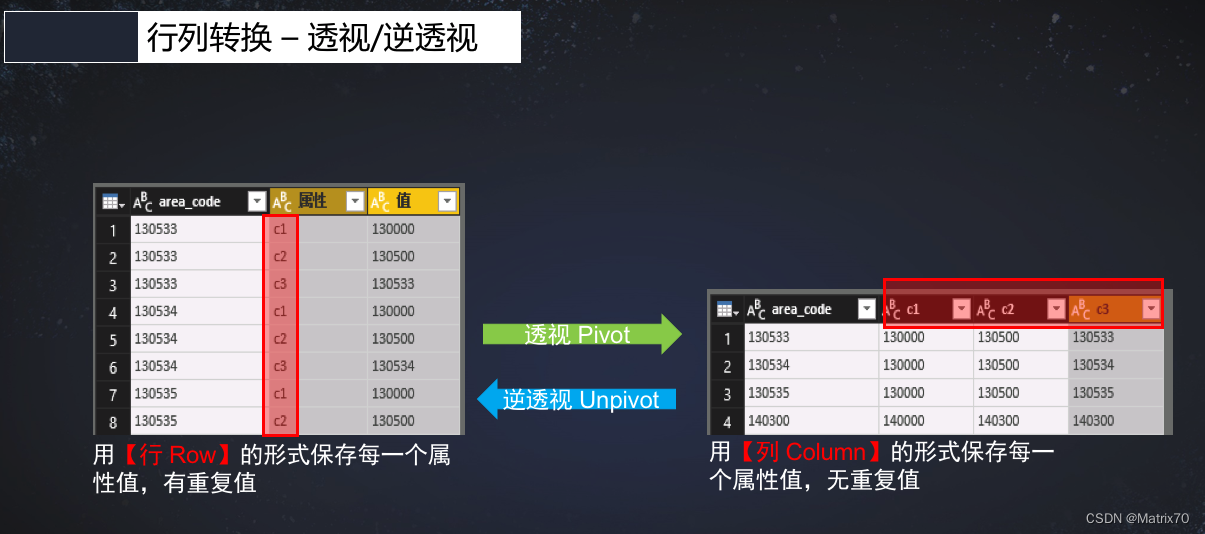
SparkOnHive_列转行、行转列生产操作(透视和逆透视)
前言 行专列,列转行是数开不可避免的一步,尤其是在最初接触Hive的时候,看到什么炸裂函数,各种udf,有点发憷,无从下手,时常产生这t怎么搞,我不会啊? 好吧ÿ…...

【人机交互 复习】第2章 Hadoop
一、概念 1.Hadoop 是一个能够对大量数据进行分布式处理的软件框架,并 且是以一种可靠、高效、可伸缩的方式进行处理的, 2.特点: 高可靠性,高效性,高可扩展性,高容错性 运行在Linux平台上,支持…...

国产自研编程语言“仓颉”来了!
在 6.21 召开的华为开发者大会(HDC2024)上,华为自研的国产编程语言“仓颉”终于对外正式发布了! 随着万物互联以及智能时代的到来,软件的形态将发生巨大的变化。一方面,移动应用和移动互联网领域仍然强力驱动人机交互…...

Swarm 集群管理
Swarm 集群管理 简介 Docker Swarm 是 Docker 的集群管理工具。它将 Docker 主机池转变为单个虚拟 Docker 主机。 Docker Swarm 提供了标准的 Docker API,所有任何已经与 Docker 守护程序通信的工具都可以使用 Swarm 轻松地扩展到多个主机。 支持的工具包括但不限…...

从社交网络到元宇宙:Facebook的战略转型
随着科技的迅猛发展和数字化时代的深入,社交网络已不再局限于简单的信息交流和社交互动,而是逐步向更广阔、更深远的虚拟现实空间——元宇宙(Metaverse)转变。作为全球最大的社交网络平台之一,Facebook正在积极推动这一…...

Qt Widget类解析与代码注释
#include "widget.h" #include "ui_widget.h"Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget) {ui->setupUi(this); }Widget::~Widget() {delete ui; }//解释这串代码,写上注释 当然可以!这段代码是 Qt …...

【快手拥抱开源】通过快手团队开源的 KwaiCoder-AutoThink-preview 解锁大语言模型的潜力
引言: 在人工智能快速发展的浪潮中,快手Kwaipilot团队推出的 KwaiCoder-AutoThink-preview 具有里程碑意义——这是首个公开的AutoThink大语言模型(LLM)。该模型代表着该领域的重大突破,通过独特方式融合思考与非思考…...

虚拟电厂发展三大趋势:市场化、技术主导、车网互联
市场化:从政策驱动到多元盈利 政策全面赋能 2025年4月,国家发改委、能源局发布《关于加快推进虚拟电厂发展的指导意见》,首次明确虚拟电厂为“独立市场主体”,提出硬性目标:2027年全国调节能力≥2000万千瓦࿰…...

2025年渗透测试面试题总结-腾讯[实习]科恩实验室-安全工程师(题目+回答)
安全领域各种资源,学习文档,以及工具分享、前沿信息分享、POC、EXP分享。不定期分享各种好玩的项目及好用的工具,欢迎关注。 目录 腾讯[实习]科恩实验室-安全工程师 一、网络与协议 1. TCP三次握手 2. SYN扫描原理 3. HTTPS证书机制 二…...

提升移动端网页调试效率:WebDebugX 与常见工具组合实践
在日常移动端开发中,网页调试始终是一个高频但又极具挑战的环节。尤其在面对 iOS 与 Android 的混合技术栈、各种设备差异化行为时,开发者迫切需要一套高效、可靠且跨平台的调试方案。过去,我们或多或少使用过 Chrome DevTools、Remote Debug…...

数学建模-滑翔伞伞翼面积的设计,运动状态计算和优化 !
我们考虑滑翔伞的伞翼面积设计问题以及运动状态描述。滑翔伞的性能主要取决于伞翼面积、气动特性以及飞行员的重量。我们的目标是建立数学模型来描述滑翔伞的运动状态,并优化伞翼面积的设计。 一、问题分析 滑翔伞在飞行过程中受到重力、升力和阻力的作用。升力和阻力与伞翼面…...
基础)
6个月Python学习计划 Day 16 - 面向对象编程(OOP)基础
第三周 Day 3 🎯 今日目标 理解类(class)和对象(object)的关系学会定义类的属性、方法和构造函数(init)掌握对象的创建与使用初识封装、继承和多态的基本概念(预告) &a…...

云安全与网络安全:核心区别与协同作用解析
在数字化转型的浪潮中,云安全与网络安全作为信息安全的两大支柱,常被混淆但本质不同。本文将从概念、责任分工、技术手段、威胁类型等维度深入解析两者的差异,并探讨它们的协同作用。 一、核心区别 定义与范围 网络安全:聚焦于保…...

二叉树-144.二叉树的前序遍历-力扣(LeetCode)
一、题目解析 对于递归方法的前序遍历十分简单,但对于一位合格的程序猿而言,需要掌握将递归转化为非递归的能力,毕竟递归调用的时候会调用大量的栈帧,存在栈溢出风险。 二、算法原理 递归调用本质是系统建立栈帧,而非…...

C#最佳实践:为何优先使用as或is而非强制转换
C#最佳实践:为何优先使用as或is而非强制转换 在 C# 的编程世界里,类型转换是我们经常会遇到的操作。就像在现实生活中,我们可能需要把不同形状的物品重新整理归类一样,在代码里,我们也常常需要将一个数据类型转换为另…...
