快速幂算法
快速幂算法
文章目录
- 快速幂算法
- 一、简单介绍
- 二、计算7107^{10}710
- 三、一般化
- 1、计算ana^nan的快速方法:
- 2、时间复杂度分析:
- 四、代码
- 五、参考资料
一、简单介绍
快速幂(Exponentiation by squaring,平方求幂)是一种简单而有效的小算法,它可以以O(logn)O(log_n)O(logn)的时间复杂度计算乘方。快速幂不仅本身非常常见,而且后续很多算法也都会用到快速幂。
二、计算7107^{10}710
让我们先来思考一个问题:7的10次方,怎样算比较快?
最朴素的想法,77=49,497=343,… 一步一步算,共进行了9次乘法。这样算无疑太慢了,尤其对计算机的CPU而言,每次运算只乘上一个个位数,无疑太屈才了。这时我们想到,也许可以拆分问题。
我们换一个角度来引入快速幂。还是7的10次方,但这次,我们把10写成二进制的形式,也就是 1010。于是这个问题就变成了求7的二进制(1010)次幂。这样就只需要计算4次,相比于9次,大大提升了效率。
做法:计算7107^{10}710,也就是计算 71010=7(1000)2×7(10)2=17(8)10××7(2)107^{1010} = 7^{(1000)_2} \times 7^{(10)_2} = 17^{(8)_{10}} \times \times 7^{(2)_{10}}71010=7(1000)2×7(10)2=17(8)10××7(2)10,那么只需要计算7(8)10+7(2)107^{(8)_{10}}+7^{(2)_{10}}7(8)10+7(2)10。更一般化,只需要计算720,721,722,...,72n7^{2^{0}},7^{2^{1}},7^{2^{2}},...,7^{2^{n}}720,721,722,...,72n。
三、一般化
1、计算ana^nan的快速方法:
(1)将nnn 转化成二进制形式,例如1011010
(2)转化后的形式为a(xkxk−1...x2x1x0)2=axk0...00×a0xk−1...00×a00...10×a00...01a^{(x_kx_{k-1}...x_2x_1x_0)_2} = a^{x_k0...00} \times a^{0x_{k-1}...00} \times a^{00...10} \times a^{00...01}a(xkxk−1...x2x1x0)2=axk0...00×a0xk−1...00×a00...10×a00...01.
(3) 需要计算的数值为a1,a2,a4,a8,....,a2na^{1},a^{2},a^{4},a^{8},....,a^{2^{n}}a1,a2,a4,a8,....,a2n.
2、时间复杂度分析:
一般求解 ana^nan 时,需要计算n次。但是使用快速幂算法之后,将nnn 表示成二进制只需要O(logn)O(log_n)O(logn) 位数字,只需要计算O(logn)O(log_n)O(logn)次。
四、代码
public static Long quickPow(Long a,Long n,Long p){//结果Long res = 1L;while (n != 0) {//判断 n 的二进制的最后一位是否为0if((n&1)!=0){//当n的二进制最后一位为1时,乘以当前的权重res = (res*a)%p;}//更新n,每次n向右移一位n = n >> 1;//更新每一位的权重a = (a*a)%p;}return res;
}
五、参考资料
[1] 基础算法—快速幂详解
[2] 快速幂算法
幂算法](https://blog.csdn.net/HouGOD/article/details/123847315)
相关文章:

快速幂算法
快速幂算法 文章目录快速幂算法一、简单介绍二、计算7107^{10}710三、一般化1、计算ana^nan的快速方法:2、时间复杂度分析:四、代码五、参考资料一、简单介绍 快速幂(Exponentiation by squaring,平方求幂)是一种简…...
Flink-1.13.1消费kafka并插入hudi)
Hudi:问题总结(2)Flink-1.13.1消费kafka并插入hudi
问题一:java.lang.ClassNotFoundException: com.google.protobuf.MessageOrBuilder) 解决:字面意思,没找到类,将protobuf-java-3.2.0-jar包放到fink/lib/下 如果报commons-cli相关的错,就将commons-cli-1.4.jar放到f…...

Application工具方法
//注册这个接口registerActivityLifecycleCallbacks(activityLifecycleCallbacks);}Overridepublic void onTerminate() {//注销这个接口。unregisterActivityLifecycleCallbacks(activityLifecycleCallbacks);super.onTerminate();}public static List<Activity> activi…...
电脑游戏怎么录屏?其实很简单,只需要简单3步
电脑游戏一直是游戏爱好者最热衷的游戏之一。但是,有时候我们想分享我们在游戏中的精彩时刻,或者记录我们的游戏过程以便后续观看和学习。在这种情况下,录屏就成了必不可少的工具。但是,许多人可能不知道电脑游戏怎么录屏。在本文…...

【设计模式】go语言中的 [函数选项,单例,工厂,责任链] 常用的设计模式
文章目录前言一、函数选项模式二、单例模式三、工厂模式四、责任链模式前言 宿舍每人 温度38℃+ 大寄 设计模式很重要,设计模式其实就是为了解决某一类问题而形成的代码写法,设计模式很多,但是并不是每个都很常用,我们…...

2017系统分析师案例分析真题背记内容
前言 以下内容仅为个人根据当年系分案例真题问题整理的偏需要记背的考点答案,方便个人背诵和记忆使用。方便文字转语音,所以内容全为纯文字内容,以下内容仅供参考。 背记内容 微服务 微服务中应该包含的内容有:资源、对资源的…...

C++和C的区别
答:从宏观角度和微观角度分析微观角度:函数原型有区别,在c中,函数原型有参数和没有参数是不同的,并且允许申明多个同名的函数,只要他们的参数列表不同或者返回值不同即可,但是在c语言中不能。C引…...
【React教程】一、React简介
一、React简介 React是一个用于构建用户界面的JavaScript库,它是Facebook的内部项目,用来架设Instagram的网站,并于2013年5月开源。React主要用于构建Ul,很多人认为React 是 MVC 中的 V(视图)。由于拥有较高的性能&…...

运动蓝牙耳机什么牌子好,比较好的运动蓝牙耳机推荐
现在市面上的运动蓝牙耳机越来越多,在选择耳机的时候应该如何入手呢?最重要的是需要按照自己的需求来选择,但在耳机的配置上不能忽视的是耳机的防水等级,运动耳机对防水等级的要求更高,这样能够更好地防御汗水浸湿耳机…...

[深入理解SSD系列 闪存实战2.1] NAND FLASH特性串烧 | 不了解闪存特性,你能用好闪存产品吗?
前言 为了利用好闪存, 发挥闪存的优势, 以达到更好的性能和使用寿命, 那自然要求了解闪存特性。 闪存作为一种相对较新的存储介质, 有很多特别的特性。 一.闪存的特性 凡是采用Flash Memory的存储设备,可以统称为闪存存储。我们经常谈的固态硬盘(SSD),可以由volatile/…...
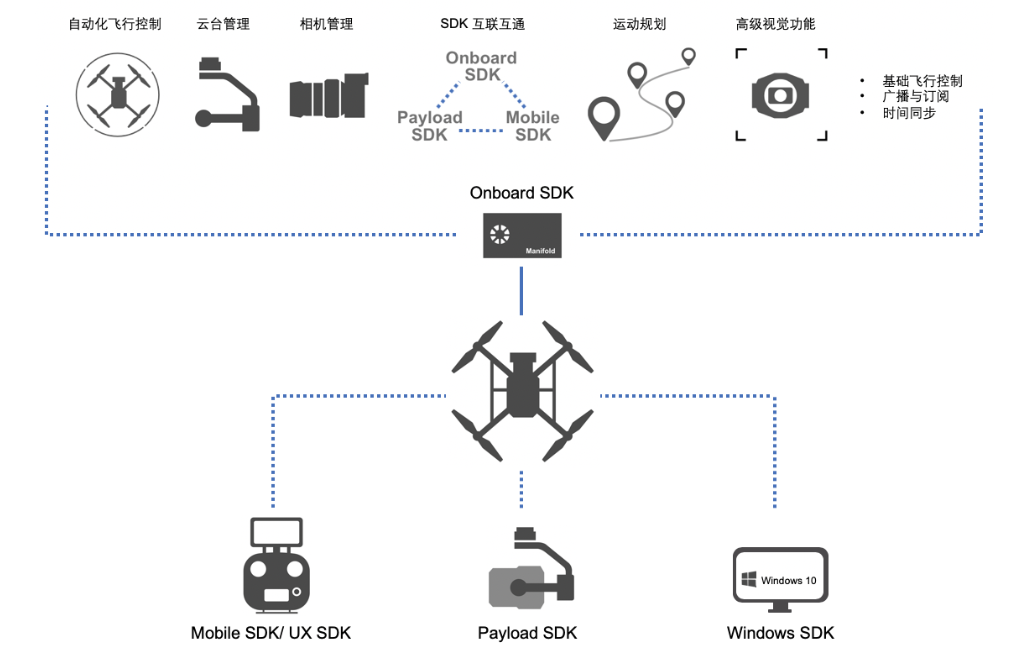
DJI ROS dji_sdk 源码分析|整体框架
DJI ROS dji_sdk 源码分析|整体框架launch文件CMakeLists.txtcpp文件main.cppOSDK 是一个用于开发无人机应用程序的开发工具包,基于OSDK 开发的应用程序能够运行在机载计算机上(如Manifold 2),开发者通过调用OSDK 中指定的接口能够…...

HT32合泰单片机开发环境搭建和配置教程
HT32合泰(Holtek)单片机开发环境搭建安装教程 前言 最近在准备合泰杯的比赛,在看合泰官方的PPT和数据手册学习,顺便做个合泰单片机的开发环境搭建教程。 合泰杯比赛发放的开发板是ESK32-30501,用的单片机是HT32F52352。 合泰杯官网地址&a…...
动态内存分配之伙伴算法
伙伴算法 伙伴算法是一种在计算机内存管理中使用的算法,用于分配和释放内存。它是一种基于二叉树的动态内存分配算法,可以高效地分配和合并内存块。伙伴算法是一种按照固定大小分配内存的算法,例如,每个内存块的大小为2的n次幂&a…...

CGAL 根据扫描线方向和角度对法向量进行重定向
目录一、算法原理1、主要函数二、代码实现一、算法原理 最小生成树对法向量定向的结果在具有许多尖锐特征和遮挡的机载点云数据中结果并不理想。scanline_orient_normals()是专门用于具有扫描线特性的点云法向量重定向的替代方法。它充分利用了某些激光雷达扫描器的LAS特性&…...
一个C#开发的开源的快速启动工具
更多开源项目请查看:一个专注推荐.Net开源项目的榜单 平常计算机安装软件比较多、或者工作涉及的文件比较多,很多人都会直接放在桌面,一方面不安全,还不容易查找,这时候我们往往,都会放在其他硬盘内&#x…...
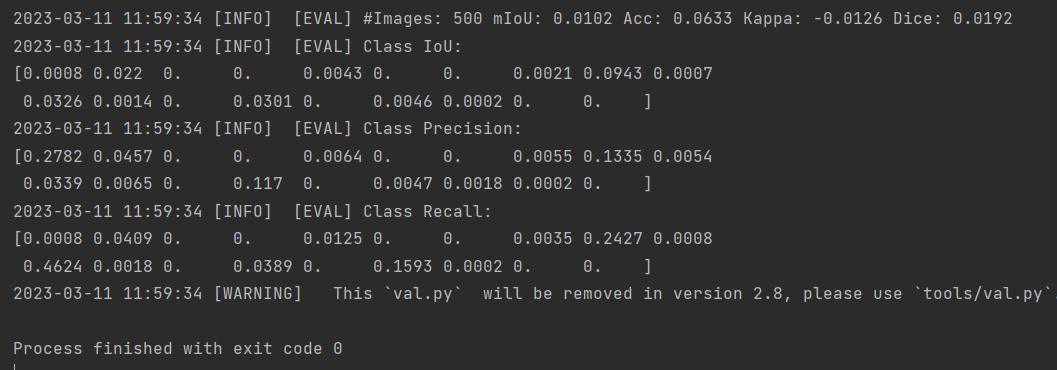
Paddle项目调试记录
PaddlePaddle是百度公司提出的深度学习框架。近年来深度学习在很多机器学习领域都有着非常出色的表现,在图像识别、语音识别、自然语言处理、机器人、网络广告投放、医学自动诊断和金融等领域有着广泛应用。面对繁多的应用场景,深度学习框架有助于建模者…...

3月11日,30秒知全网,精选7个热点
///微盟集团宣布接入百度文心一言 据介绍,微盟SaaS产品和数字营销服务将与文心一言的技术能力实现深度融合,通过AIGC技术,深化微盟在营销AI创意内容生产、智能营销、智能客服、智能经营等方面的布局 ///T3出行与华为云深化业务合作 双方将在…...
)
C win32基础学习(四)
上一篇我们已经介绍了关于窗口处理函数的知识。本篇我们说一下注册窗口类,创建窗口和显示窗口的内容。 前文 窗口创建过程 定义WinMain函数 定义窗口处理函数(自定义,处理消息) 注册窗口类(向操作系统写入一些数据) 创建窗口&…...
)
Java 日期时间API(Java 8及以上)
Java 8及以上版本提供了新的日期时间API,其中包括了LocalDate、LocalTime、LocalDateTime、ZonedDateTime、Duration、Period等类,这些类提供了更加丰富和灵活的日期时间操作方法。 LocalDate LocalDate类表示一个本地日期,不包含时间和时区…...

DHCP的配置
实验目的熟悉DHCP的应用场景掌握DHCP的配置方法实验拓扑DHCP的配置如图15-2所示: 图15-2:DHCP的配置 实验步骤配置IP地址<Huawei>system-view Enter system view, return user view with Ctrl+Z....

深入浅出Asp.Net Core MVC应用开发系列-AspNetCore中的日志记录
ASP.NET Core 是一个跨平台的开源框架,用于在 Windows、macOS 或 Linux 上生成基于云的新式 Web 应用。 ASP.NET Core 中的日志记录 .NET 通过 ILogger API 支持高性能结构化日志记录,以帮助监视应用程序行为和诊断问题。 可以通过配置不同的记录提供程…...

【2025年】解决Burpsuite抓不到https包的问题
环境:windows11 burpsuite:2025.5 在抓取https网站时,burpsuite抓取不到https数据包,只显示: 解决该问题只需如下三个步骤: 1、浏览器中访问 http://burp 2、下载 CA certificate 证书 3、在设置--隐私与安全--…...
指令的指南)
在Ubuntu中设置开机自动运行(sudo)指令的指南
在Ubuntu系统中,有时需要在系统启动时自动执行某些命令,特别是需要 sudo权限的指令。为了实现这一功能,可以使用多种方法,包括编写Systemd服务、配置 rc.local文件或使用 cron任务计划。本文将详细介绍这些方法,并提供…...

Spring Boot面试题精选汇总
🤟致敬读者 🟩感谢阅读🟦笑口常开🟪生日快乐⬛早点睡觉 📘博主相关 🟧博主信息🟨博客首页🟫专栏推荐🟥活动信息 文章目录 Spring Boot面试题精选汇总⚙️ **一、核心概…...

稳定币的深度剖析与展望
一、引言 在当今数字化浪潮席卷全球的时代,加密货币作为一种新兴的金融现象,正以前所未有的速度改变着我们对传统货币和金融体系的认知。然而,加密货币市场的高度波动性却成为了其广泛应用和普及的一大障碍。在这样的背景下,稳定…...

Yolov8 目标检测蒸馏学习记录
yolov8系列模型蒸馏基本流程,代码下载:这里本人提交了一个demo:djdll/Yolov8_Distillation: Yolov8轻量化_蒸馏代码实现 在轻量化模型设计中,**知识蒸馏(Knowledge Distillation)**被广泛应用,作为提升模型…...

R 语言科研绘图第 55 期 --- 网络图-聚类
在发表科研论文的过程中,科研绘图是必不可少的,一张好看的图形会是文章很大的加分项。 为了便于使用,本系列文章介绍的所有绘图都已收录到了 sciRplot 项目中,获取方式: R 语言科研绘图模板 --- sciRplothttps://mp.…...
)
【LeetCode】3309. 连接二进制表示可形成的最大数值(递归|回溯|位运算)
LeetCode 3309. 连接二进制表示可形成的最大数值(中等) 题目描述解题思路Java代码 题目描述 题目链接:LeetCode 3309. 连接二进制表示可形成的最大数值(中等) 给你一个长度为 3 的整数数组 nums。 现以某种顺序 连接…...

uniapp 小程序 学习(一)
利用Hbuilder 创建项目 运行到内置浏览器看效果 下载微信小程序 安装到Hbuilder 下载地址 :开发者工具默认安装 设置服务端口号 在Hbuilder中设置微信小程序 配置 找到运行设置,将微信开发者工具放入到Hbuilder中, 打开后出现 如下 bug 解…...

aardio 自动识别验证码输入
技术尝试 上周在发学习日志时有网友提议“在网页上识别验证码”,于是尝试整合图像识别与网页自动化技术,完成了这套模拟登录流程。核心思路是:截图验证码→OCR识别→自动填充表单→提交并验证结果。 代码在这里 import soImage; import we…...
