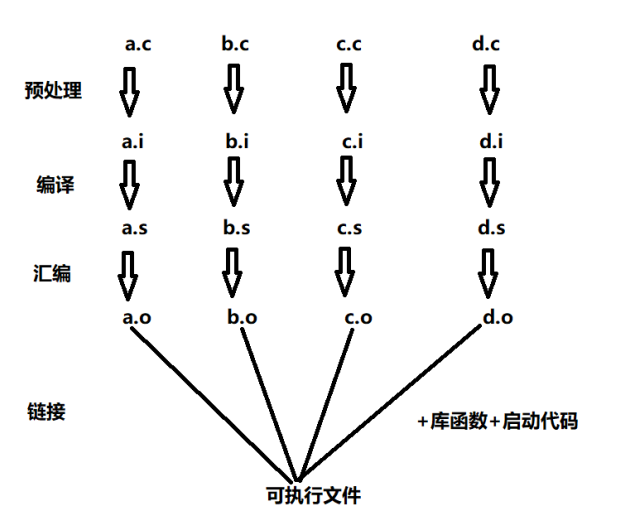
gcc 编译的过程
#include <stdio.h>
#define PI 3.14
int main(int argc, char const *argv[])
{
//打印IP的值printf("PI = %lf\n", PI);return 0;
}编译的过程:预处理、编译、汇编、链接
1.预处理:宏替换、删除注释、头文件包含、条件编译 -E (不会报语法错误)
gcc ‐E hello.c ‐o hello.i 1、预处理
2.编译:将预处理后的文件 编译成 汇编文件 (报语法错误)
gcc ‐S hello.i –o hello.s 2、编译
3.汇编:将汇编文件 生成 二进制文件
gcc ‐c hello.s ‐o hello.o 3、汇编
4.链接:将工程的二进制文件 +库函数+启动代码 生成可执行文件
gcc hello.o ‐o hello_elf 4、链接
一步到位:
1.gcc main.c ‐o main
2 gcc main.c
相关文章:

gcc 编译的过程
#include <stdio.h> #define PI 3.14 int main(int argc, char const *argv[]) { //打印IP的值printf("PI %lf\n", PI);return 0; }编译的过程:预处理、编译、汇编、链接1.预处理:宏替换、删除注释、头文件包含、条件编译 -E …...

Hadoop入个门
文章目录1️⃣、Hadoop概述1.1、Hadoop是什么1.2、三大发行版本1.3、优势1.4、组成HDFSYARNMapReduceHDFS、YARN、MapReduce三者关系1.6、大数据技术生态体系image-202303111027195802️⃣、Hadoop运行环境搭建2.1、虚拟机环境准备2.2、克隆虚拟机2.3、在hadoop2上安装JDK2.4、…...
python 从0到批量下载某站视频
简介:真实从0到1,童叟无欺~ 目标:用python批量下载某站搜索视频,以“CG 服装”为例 本章主要介绍如何用python把搜索到的视频直接下载到自己的本地文件夹中~ 介绍一下工作流1. 下载并安装python2. 测试pyt…...
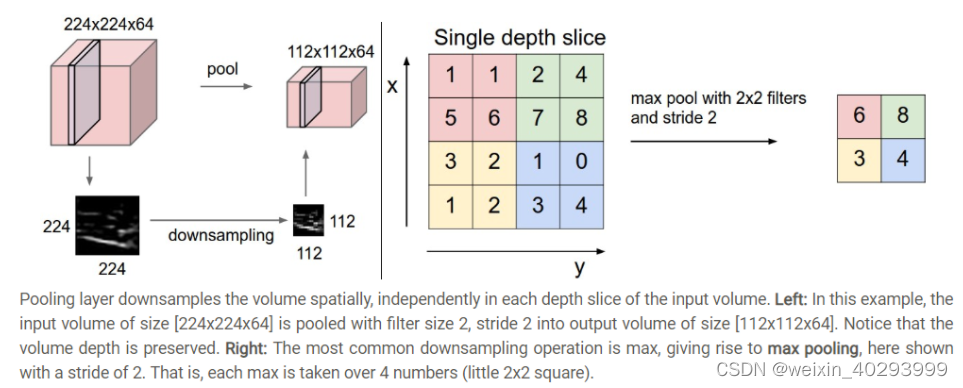
【深度学习】神经网络和深度学习--卷积和池化的作用
深度学习通常指训练大型深度的神经网络的过程。 与传统的神经网络模型相比,深度学习模型在结构上与之非常相似;不同的是,深度学习模型的“深度”更大,“深度”的体现就是神经网络层数多,神经网络每一层的结点数多。 本…...

锦正茂风冷系列电源JCP-10-80的技术参数
JCP-10-80为高稳定度的双极性恒流电源,广泛应用于电磁铁、亥姆霍兹线圈等感性负载的励磁。电源采用线性电源结构,输出电流稳定度高,纹波和噪声低。电源输出电流可在正负额定电流*值之间连续变化,电流平滑连续过零,可使…...
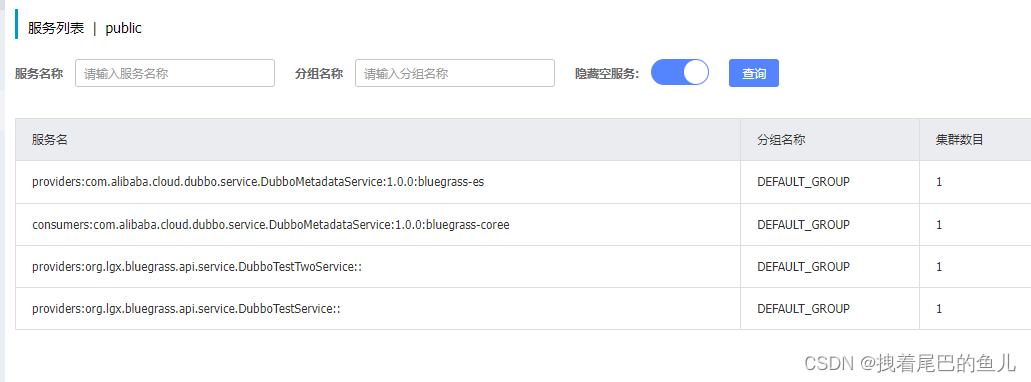
Idea+maven+spring-cloud项目搭建系列--11-1 dubbo(zookeeper,nacos)注册中心
前言:dubbo rpc 服务需要将服务提供者和消费者信息进行注册,以便于消费端可以完成远程接口调用;注册中心是 Dubbo 服务治理的核心组件,Dubbo 依赖注册中心的协调实现服务(地址)发现,自动化的服务…...

Python3入门教程||Python3 迭代器与生成器||Python3 函数
Python3 迭代器与生成器 迭代器 迭代是 Python 最强大的功能之一,是访问集合元素的一种方式。。 迭代器是一个可以记住遍历的位置的对象。 迭代器对象从集合的第一个元素开始访问,直到所有的元素被访问完结束。迭代器只能往前不会后退。 迭代器有两…...

快速幂算法
快速幂算法 文章目录快速幂算法一、简单介绍二、计算7107^{10}710三、一般化1、计算ana^nan的快速方法:2、时间复杂度分析:四、代码五、参考资料一、简单介绍 快速幂(Exponentiation by squaring,平方求幂)是一种简…...
Flink-1.13.1消费kafka并插入hudi)
Hudi:问题总结(2)Flink-1.13.1消费kafka并插入hudi
问题一:java.lang.ClassNotFoundException: com.google.protobuf.MessageOrBuilder) 解决:字面意思,没找到类,将protobuf-java-3.2.0-jar包放到fink/lib/下 如果报commons-cli相关的错,就将commons-cli-1.4.jar放到f…...

Application工具方法
//注册这个接口registerActivityLifecycleCallbacks(activityLifecycleCallbacks);}Overridepublic void onTerminate() {//注销这个接口。unregisterActivityLifecycleCallbacks(activityLifecycleCallbacks);super.onTerminate();}public static List<Activity> activi…...
电脑游戏怎么录屏?其实很简单,只需要简单3步
电脑游戏一直是游戏爱好者最热衷的游戏之一。但是,有时候我们想分享我们在游戏中的精彩时刻,或者记录我们的游戏过程以便后续观看和学习。在这种情况下,录屏就成了必不可少的工具。但是,许多人可能不知道电脑游戏怎么录屏。在本文…...

【设计模式】go语言中的 [函数选项,单例,工厂,责任链] 常用的设计模式
文章目录前言一、函数选项模式二、单例模式三、工厂模式四、责任链模式前言 宿舍每人 温度38℃+ 大寄 设计模式很重要,设计模式其实就是为了解决某一类问题而形成的代码写法,设计模式很多,但是并不是每个都很常用,我们…...

2017系统分析师案例分析真题背记内容
前言 以下内容仅为个人根据当年系分案例真题问题整理的偏需要记背的考点答案,方便个人背诵和记忆使用。方便文字转语音,所以内容全为纯文字内容,以下内容仅供参考。 背记内容 微服务 微服务中应该包含的内容有:资源、对资源的…...

C++和C的区别
答:从宏观角度和微观角度分析微观角度:函数原型有区别,在c中,函数原型有参数和没有参数是不同的,并且允许申明多个同名的函数,只要他们的参数列表不同或者返回值不同即可,但是在c语言中不能。C引…...
【React教程】一、React简介
一、React简介 React是一个用于构建用户界面的JavaScript库,它是Facebook的内部项目,用来架设Instagram的网站,并于2013年5月开源。React主要用于构建Ul,很多人认为React 是 MVC 中的 V(视图)。由于拥有较高的性能&…...

运动蓝牙耳机什么牌子好,比较好的运动蓝牙耳机推荐
现在市面上的运动蓝牙耳机越来越多,在选择耳机的时候应该如何入手呢?最重要的是需要按照自己的需求来选择,但在耳机的配置上不能忽视的是耳机的防水等级,运动耳机对防水等级的要求更高,这样能够更好地防御汗水浸湿耳机…...

[深入理解SSD系列 闪存实战2.1] NAND FLASH特性串烧 | 不了解闪存特性,你能用好闪存产品吗?
前言 为了利用好闪存, 发挥闪存的优势, 以达到更好的性能和使用寿命, 那自然要求了解闪存特性。 闪存作为一种相对较新的存储介质, 有很多特别的特性。 一.闪存的特性 凡是采用Flash Memory的存储设备,可以统称为闪存存储。我们经常谈的固态硬盘(SSD),可以由volatile/…...
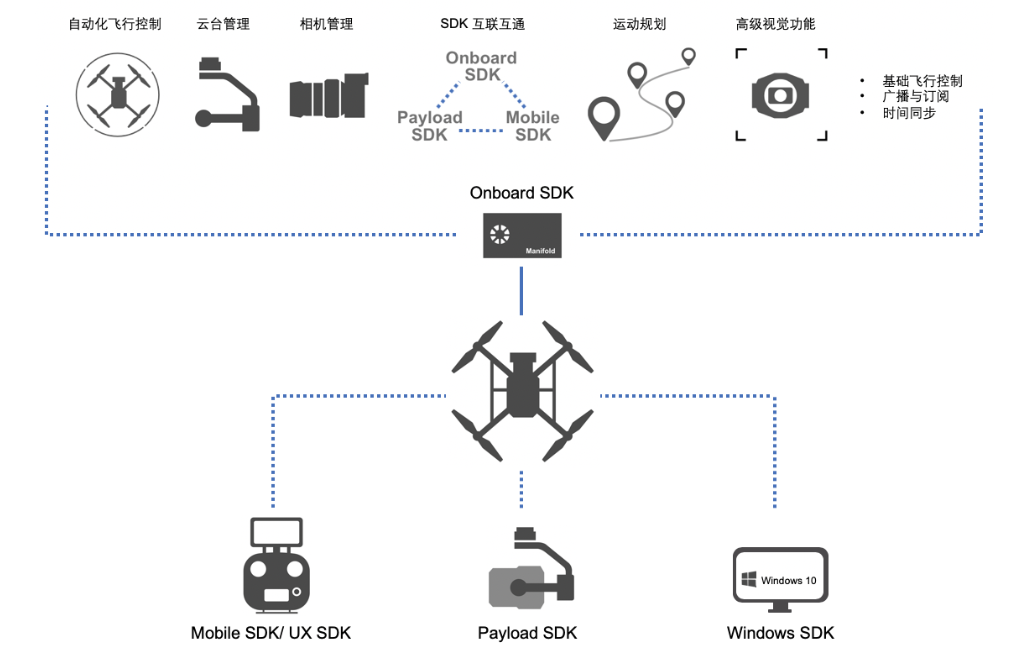
DJI ROS dji_sdk 源码分析|整体框架
DJI ROS dji_sdk 源码分析|整体框架launch文件CMakeLists.txtcpp文件main.cppOSDK 是一个用于开发无人机应用程序的开发工具包,基于OSDK 开发的应用程序能够运行在机载计算机上(如Manifold 2),开发者通过调用OSDK 中指定的接口能够…...

HT32合泰单片机开发环境搭建和配置教程
HT32合泰(Holtek)单片机开发环境搭建安装教程 前言 最近在准备合泰杯的比赛,在看合泰官方的PPT和数据手册学习,顺便做个合泰单片机的开发环境搭建教程。 合泰杯比赛发放的开发板是ESK32-30501,用的单片机是HT32F52352。 合泰杯官网地址&a…...
动态内存分配之伙伴算法
伙伴算法 伙伴算法是一种在计算机内存管理中使用的算法,用于分配和释放内存。它是一种基于二叉树的动态内存分配算法,可以高效地分配和合并内存块。伙伴算法是一种按照固定大小分配内存的算法,例如,每个内存块的大小为2的n次幂&a…...

PHP和Node.js哪个更爽?
先说结论,rust完胜。 php:laravel,swoole,webman,最开始在苏宁的时候写了几年php,当时觉得php真的是世界上最好的语言,因为当初活在舒适圈里,不愿意跳出来,就好比当初活在…...

23-Oracle 23 ai 区块链表(Blockchain Table)
小伙伴有没有在金融强合规的领域中遇见,必须要保持数据不可变,管理员都无法修改和留痕的要求。比如医疗的电子病历中,影像检查检验结果不可篡改行的,药品追溯过程中数据只可插入无法删除的特性需求;登录日志、修改日志…...

uni-app学习笔记二十二---使用vite.config.js全局导入常用依赖
在前面的练习中,每个页面需要使用ref,onShow等生命周期钩子函数时都需要像下面这样导入 import {onMounted, ref} from "vue" 如果不想每个页面都导入,需要使用node.js命令npm安装unplugin-auto-import npm install unplugin-au…...

理解 MCP 工作流:使用 Ollama 和 LangChain 构建本地 MCP 客户端
🌟 什么是 MCP? 模型控制协议 (MCP) 是一种创新的协议,旨在无缝连接 AI 模型与应用程序。 MCP 是一个开源协议,它标准化了我们的 LLM 应用程序连接所需工具和数据源并与之协作的方式。 可以把它想象成你的 AI 模型 和想要使用它…...

相机从app启动流程
一、流程框架图 二、具体流程分析 1、得到cameralist和对应的静态信息 目录如下: 重点代码分析: 启动相机前,先要通过getCameraIdList获取camera的个数以及id,然后可以通过getCameraCharacteristics获取对应id camera的capabilities(静态信息)进行一些openCamera前的…...

自然语言处理——循环神经网络
自然语言处理——循环神经网络 循环神经网络应用到基于机器学习的自然语言处理任务序列到类别同步的序列到序列模式异步的序列到序列模式 参数学习和长程依赖问题基于门控的循环神经网络门控循环单元(GRU)长短期记忆神经网络(LSTM)…...
:邮件营销与用户参与度的关键指标优化指南)
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南 在数字化营销时代,邮件列表效度、用户参与度和网站性能等指标往往决定着创业公司的增长成败。今天,我们将深入解析邮件打开率、网站可用性、页面参与时…...

AspectJ 在 Android 中的完整使用指南
一、环境配置(Gradle 7.0 适配) 1. 项目级 build.gradle // 注意:沪江插件已停更,推荐官方兼容方案 buildscript {dependencies {classpath org.aspectj:aspectjtools:1.9.9.1 // AspectJ 工具} } 2. 模块级 build.gradle plu…...

C# 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

学校时钟系统,标准考场时钟系统,AI亮相2025高考,赛思时钟系统为教育公平筑起“精准防线”
2025年#高考 将在近日拉开帷幕,#AI 监考一度冲上热搜。当AI深度融入高考,#时间同步 不再是辅助功能,而是决定AI监考系统成败的“生命线”。 AI亮相2025高考,40种异常行为0.5秒精准识别 2025年高考即将拉开帷幕,江西、…...
