牛客小白月赛68
牛客小白月赛68
- A Tokitsukaze and New Operation
- B Tokitsukaze and Order Food Delivery
- C Tokitsukaze and Average of Substring
- D Tokitsukaze and Development Task
- E Tokitsukaze and Colorful Chessboard
- F Tokitsukaze and New RenKinKama
题目链接
A Tokitsukaze and New Operation
思路:
读入时将整数按字符串读入,直接模拟即可
代码:
#include <bits/stdc++.h>using namespace std;string solve()
{string a,b;cin >> a >> b;if(a.length() != b.length()) return "-1";string ans = "";for(int i = 0; i < a.length();i++){int x = (a[i] - '0') * (b[i] - '0');ans += to_string(x);}return ans;
}int main(){int t;cin >> t ;while(t--){cout << solve() << endl;}return 0;
}
B Tokitsukaze and Order Food Delivery
思路:
按题意模拟更新求最值
代码:
#include <bits/stdc++.h>using namespace std;int solve()
{int n , a , b;int ans = 2e9;cin >> n >> a >> b;for(int i = 0; i < n; i++){int k , x , y; cin >> k >> x >> y;for(int j = 0; j < k; j++){int z;cin >> z;int d = 0;if(z >= x) d += y;if(z >= a) d += b;ans = min(ans,max(z-d,0)) ;}}return ans;
}int main(){int t ;cin >> t;while(t--){cout << solve() << endl;}return 0;
}
C Tokitsukaze and Average of Substring
思路:
预处理 ‘a’ ~ ‘z’ 每种字母出现次数的前缀和,暴力枚举区间 [lll,rrr], 利用已知信息求出分子和分母,更新 FFF(lll,rrr)的最值。
代码:
#include <bits/stdc++.h>using namespace std;
const int N = 5010;
int sum[N][30];void solve()
{char s[5010];int n;scanf("%d",&n);scanf("%s",s+1);for(int i = 1; i <= n; i++){for(int j = 0; j < 26; j++) sum[i][j] = sum[i-1][j];sum[i][s[i]-'a']++;}double ans = 0;for(int l = 1; l <= n; l++){for(int r = l + 1; r <= n; r++){int up = 0;for(int j = 0; j < 26; j++){int d = sum[r][j] - sum[l-1][j];if(d >= 2) up += d * (d - 1) / 2;}ans = max(ans,up*1.0/(double )(r-l+1));}}ans = ans + 1e-8;printf("%.6f\n",ans);
}int main(){int t;cin >> t;while (t--){solve();}return 0;
}
D Tokitsukaze and Development Task
思路:
不难看出,四部分相互独立。先BFS预处理到达任意状态(10~300)的最小代价表 dis,对于每组询问,四部分的最小代价累加就是总的最小代价。
代码:
#include <bits/stdc++.h>using namespace std;
const int N = 5010;
int dis[510];
int dx[] = {1,-1,10,-10,100,-100};
void BFS()
{dis[10] = 1;queue<int>q;q.push(10);while (!q.empty()){int top = q.front();q.pop();if(!dis[300]) {dis[300] = dis[top] + 1;q.push(300);}if(!dis[10]){dis[10] = dis[top] + 1;q.push(10);}for(int i = 0; i < 6; i++){int xx = top + dx[i];if(xx < 10 || xx > 300) continue;if(dis[xx]) continue;dis[xx] = dis[top] + 1;q.push(xx);}}
}int main(){BFS();int t;scanf("%d",&t);while (t--){int a,b,c,d;scanf("%d%d%d%d",&a,&b,&c,&d);int ans = dis[a] + dis[b] + dis[c] + dis[d] - 4;printf("%d\n",ans);}return 0;
}
E Tokitsukaze and Colorful Chessboard
思路:
对于一个 nnn ∗*∗ nnn 的盘面,令 SSS = nnn ∗*∗ nnn, 可得最优划分方案(MaxaMax_aMaxa,MaxbMax_bMaxb)=(SSS /// 222,SSS /// 222 +++ SSS % 222),不妨令 b 为 a 和 b 中的较大者,满足 a ≤ MaxaMax_aMaxa 且 b ≤ MaxbMax_bMaxb,就能放入这个盘面。题目要求盘面尽可能地小,因此二分答案求最小边长。
代码:
#include <bits/stdc++.h>
#define int long long using namespace std;bool check(int d, int a, int b)
{int L = d * d / 2;int R = d * d / 2;if((d * d)%2) R++;if(L >= a && R >= b) return true;else return false ;
}int solve()
{int a, b; cin >> a >> b;if(a > b) swap(a,b);int l = 1 , r = 1e9;while(l + 1 < r) {int mid = (l + r) >> 1;if(check(mid,a,b)) r = mid;else l = mid;}if(check(l,a,b)) r = l;return r;
}signed main()
{int t;cin >> t;while (t--){cout << solve() << endl;}
}
F Tokitsukaze and New RenKinKama
思路:
先做一次任意交换(也可以交换自身,等于不交换),两重循环( O(nnn*nnn )),
这时候会有两种情况:
(1)如果经过某次交换,序列恰好能成优环,solve函数返回长度为 1 的操作序列
(2)如果经过某次交换,序列仍为劣环,必然存在至少一条劣边 e ,e两侧的点{x,y}中必然有一个要与其他点进行交换,才有可能使劣e边成为优边E,进而可能促使优环的出现。总之,第二次操作必然要修复某一条劣边(这里可以用反证法想一下)。
一点儿细节:
对于每次交换,可以O (1) 的判断新生成的环是否为优环。
优边权值记为 0 ,劣边权值记为 1 ,环的权值 exd 就是边的总权值。显然,每次交换操作只会改动很少的几条边,因此不必遍历整个环,通过改动后Exd的值就能判断环上的边是否全优(Exd = 0 时 ,全是优边,出现优环)
总的时间复杂度 OOO (((n3n^3n3)))
代码:
#include <bits/stdc++.h>using namespace std;const int N = 305;
int n,k;
bool check(int *a)
{for(int i = 1; i <= n; i++){int las = i - 1;if(las == 0)las = n;if(abs(a[i]-a[las]) > k) return false ;}return true;
}bool modify(int f, vector<pair<int,int>> &op, int *a)
{int exd = 0;for(int i = 1; i <= n; i++){int las = i - 1;if(las <= 0) las = n;exd += (abs(a[i]-a[las]) > k);}for(int i = 1; i <= n; i++){if(i == f) continue;int m1 = i;int l1 = i - 1 <= 0 ? n : i - 1;int r1 = i + 1 > n ? 1 : i + 1;int m2 = f;int l2 = f - 1 <= 0 ? n : f - 1;int r2 = f + 1 > n ? 1 : f + 1;int Exd = exd;if(m1 == l2 || m1 == r2){if(m1 == l2){Exd -= (abs(a[m1] - a[l1]) > k);Exd -= (abs(a[r2] - a[m2]) > k);Exd += (abs(a[m2] - a[l1]) > k);Exd += (abs(a[r2] - a[m1]) > k);}else {Exd -= (abs(a[m2] - a[l2]) > k);Exd -= (abs(a[r1] - a[m1]) > k);Exd += (abs(a[m1] - a[l2]) > k);Exd += (abs(a[r1] - a[m2]) > k);}}else {Exd -= (abs(a[m1] - a[l1]) > k);Exd -= (abs(a[r1] - a[m1]) > k);Exd -= (abs(a[m2] - a[l2]) > k);Exd -= (abs(a[r2] - a[m2]) > k);Exd += (abs(a[m2] - a[l1]) > k);Exd += (abs(a[r1] - a[m2]) > k);Exd += (abs(a[m1] - a[l2]) > k);Exd += (abs(a[r2] - a[m1]) > k);}if(Exd == 0){op.push_back({f,i});return true;}}return false ;
}
vector<pair<int,int>> solve()
{int a[N];cin >> n >> k;for(int i = 1; i <= n; i++){cin >> a[i];}vector<pair<int,int>>op;for(int i = 1; i <= n; i++){for(int j = i; j <= n; j++){op.push_back({i,j});swap(a[i],a[j]);if(check(a)) return op;else {int f = 1;for(int t = 1; t <= n; t++){if(t == 1) {if(abs(a[t] - a[n]) > k) {f = t;break;}}else{if(abs(a[t] - a[t-1]) > k){f = t;break;}}}int m1 = f - 1 , m2 = f;if(m1 <= 0) m1 = n;if(modify(m1,op,a)) return op;if(modify(m2,op,a)) return op;}swap(a[i],a[j]);op.pop_back();}}vector<pair<int,int>> re;return re;
}int main(){//freopen("in.txt","r",stdin);int t;cin >> t;while (t--){vector<pair<int,int>> ans = solve();if(ans.empty()) cout << -1 << endl;else {cout << ans.size() << endl;for(auto it : ans){cout << it.first << " " << it.second << endl;}}}return 0;
}
相关文章:

牛客小白月赛68
牛客小白月赛68A Tokitsukaze and New OperationB Tokitsukaze and Order Food DeliveryC Tokitsukaze and Average of SubstringD Tokitsukaze and Development TaskE Tokitsukaze and Colorful ChessboardF Tokitsukaze and New RenKinKama题目链接A Tokitsukaze and New Ope…...

【id:21】【20分】A. DS单链表--类实现
题目描述用C语言和类实现单链表,含头结点属性包括:data数据域、next指针域操作包括:插入、删除、查找注意:单链表不是数组,所以位置从1开始对应首结点,头结点不放数据类定义参考输入n第1行先输入n表示有n个…...

【实习_面试全程辅导分享】简历篇
🎋🎋哈喽,大家好,我是辰柒。快有一个月没有更新博文啦,那么这一个月不是在偷懒,而是在全心准备找实习的过程中。那么最终也是拿到了心仪的大厂offer——海康威视!!经过这次找实习的经历,我想就在校大学生找实习这件事情开设一个专栏,帮助大家在找实习的过程中减少焦…...

【学习笔记】CF1305 Kuroni and Antihype
想了一下,觉得还是发单篇的题解比较合理 怎么感觉这题之前做过 先抛开建边方式不管 这一步其实挺重要的,但是可能大多数人独立做这道题的时候都在想用位运算的性质,而没有想到分开考虑吧?,考虑新建000号节点…...

json-server单独使用或者在react中进行使用
json-serverjson-server使用教程修改json-server端口号启动1、全局安装json-server2、在根目录生成一个db.json3、启动 访问react中进行使用react中修改json-server启动端口号1、 第一步也是安装,和第一种一样2、在根路径下定义一个__json_server_mock__文件夹3、在…...

【6G 新技术】6G数据面介绍
博主未授权任何人或组织机构转载博主任何原创文章,感谢各位对原创的支持! 博主链接 本人就职于国际知名终端厂商,负责modem芯片研发。 在5G早期负责终端数据业务层、核心网相关的开发工作,目前牵头6G算力网络技术标准研究。 博客…...
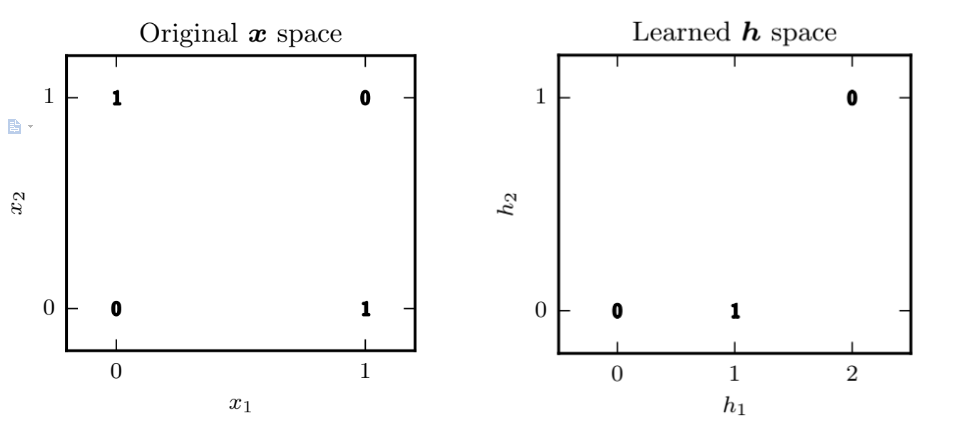
【AI绘图学习笔记】深度前馈网络(一)
有关深度前馈网络的部分知识,我们已经在吴恩达的机器学习课程中有过了解了,本章主要是对《深度学习》花书中第六章:深度前馈网络的总结笔记。我希望你在看到这一章的时候,能回忆起机器学习课程中的一些环节或者细节,这…...

目标检测笔记合集
目标检测笔记合集1. 必看的两篇目标检测论文2. 必速看的深度学习目标检测的论文集及概述2.1 一份Slide(PPT)两张表格带你快速了解目标检测2.2 最新目标检测算法回顾2022笔记合集3.目标检测的应用与需求4.目标检测的定义与挑战5.目标检测损失函数的进展6.目标检测IOU…...

《计算机网络》期末复习笔记
文章目录一、一些英文名词的标签(方便记忆)二、OSI七层协议三、综合题3.0 知识点储备3.1 在Internet 网中,某计算机的IP 地址是11001010.01100000.00101100.01011000 ,请回答下列问题3.2 假定发送方要发送的数据为10000101。采用C…...
linux下安装SonarQube
目录1. 准备安装环境2. 安装postgres数据库3. 安装SonarQube4. 使用SonarQube1. 准备安装环境 这里安装SonarQube的系统环境是Red Hat Enterprise Linux release 8.7 ,然后将jdk的压缩包(jdk-17.0.2_linux-x64_bin.tar.gz)和sonarQube的压缩…...

MyBatis-Plus(狂神)
一.特点 无侵入:只做增强不做改变,引入它不会对现有工程产生影响,如丝般顺滑损耗小:启动即会自动注入基本 CURD,性能基本无损耗,直接面向对象操作强大的 CRUD 操作:内置通用 Mapper、通用 Serv…...

Python3实现写作
导语T_T没有科研梦想的人半夜过来水篇文章~~~让Python学会写写歌,创创作~~~纯属娱乐~~~改编自PyTorch官网的一个教程,不过我用TF写的,然后生成英文变成了生成中文~~~Lets Go~~~相关文件百度网盘下载链接: https://pan.baidu.com/s/1VUEFR82Cq…...

UEFI实战--------HII之uni文件
uni文件 HII的实现涉及到多种不同类型的文件,uni文件是其中最简单的一种,它用来存放各种语言的字符串以实现本地化。本节主要参考自《edk-ii-uni-specification.pdf》,后面简称为参考文档。 关于uni文件的作用,在参考文档中做了如…...

基于Spring Boot集成MyBatis-3.5.9操作数据库
记录:382场景:在Spring Boot 2.6.3中集成MyBatis 3.5.9操作数据库。实现MyBatis的查、增、改、删操作数据库示例。MyBatis官网:http://www.mybatis.org/MyBatis源码:https://github.com/mybatis/1.初始化准备1.1创建Maven工程使用…...

了解国外SEO负面压制的现状与应对策略!
随着全球化的发展,越来越多的企业和品牌开始将目光转向海外市场,而谷歌作为全球最大的搜索引擎之一,也成为了外贸企业最主要的搜索引擎之一。 然而,随着谷歌的不断发展,国外SEO负面压制的现状也愈发严峻,外…...

Yolov5-交通标志检测与识别
项目介绍 上一篇文章介绍了基于卷积神经网络的交通标志分类识别Python交通标志识别基于卷积神经网络的保姆级教程(Tensorflow),并且最后实现了一个pyqt5的GUI界面,并且还制作了一个简单的Falsk前端网页实现了前后端的一个简单交互…...
)
Linux内核Thermal框架详解五、Thermal Core(4)
本文部分内容参考Linux Thermal 学习笔记 - 爱码网。特此致谢! 接前一篇文章Linux内核Thermal框架详解四、Thermal Core(3) 三、相关源码及分析 2. thermal_register_governors 上一回说到这一段代码: for (__governor __gove…...
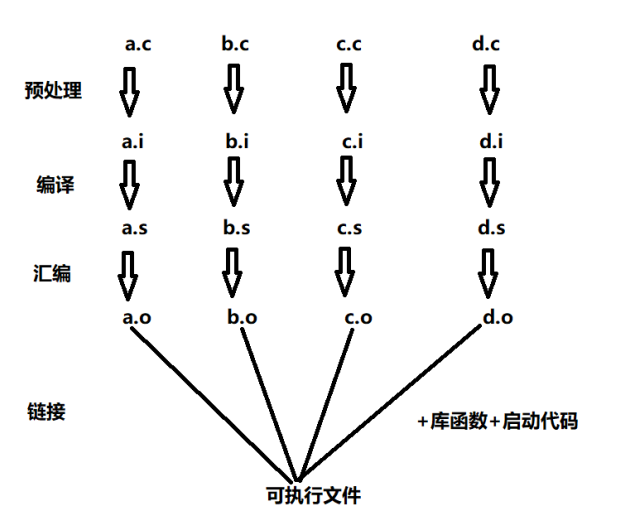
gcc 编译的过程
#include <stdio.h> #define PI 3.14 int main(int argc, char const *argv[]) { //打印IP的值printf("PI %lf\n", PI);return 0; }编译的过程:预处理、编译、汇编、链接1.预处理:宏替换、删除注释、头文件包含、条件编译 -E …...

Hadoop入个门
文章目录1️⃣、Hadoop概述1.1、Hadoop是什么1.2、三大发行版本1.3、优势1.4、组成HDFSYARNMapReduceHDFS、YARN、MapReduce三者关系1.6、大数据技术生态体系image-202303111027195802️⃣、Hadoop运行环境搭建2.1、虚拟机环境准备2.2、克隆虚拟机2.3、在hadoop2上安装JDK2.4、…...
python 从0到批量下载某站视频
简介:真实从0到1,童叟无欺~ 目标:用python批量下载某站搜索视频,以“CG 服装”为例 本章主要介绍如何用python把搜索到的视频直接下载到自己的本地文件夹中~ 介绍一下工作流1. 下载并安装python2. 测试pyt…...

React 第五十五节 Router 中 useAsyncError的使用详解
前言 useAsyncError 是 React Router v6.4 引入的一个钩子,用于处理异步操作(如数据加载)中的错误。下面我将详细解释其用途并提供代码示例。 一、useAsyncError 用途 处理异步错误:捕获在 loader 或 action 中发生的异步错误替…...

css实现圆环展示百分比,根据值动态展示所占比例
代码如下 <view class""><view class"circle-chart"><view v-if"!!num" class"pie-item" :style"{background: conic-gradient(var(--one-color) 0%,#E9E6F1 ${num}%),}"></view><view v-else …...

将对透视变换后的图像使用Otsu进行阈值化,来分离黑色和白色像素。这句话中的Otsu是什么意思?
Otsu 是一种自动阈值化方法,用于将图像分割为前景和背景。它通过最小化图像的类内方差或等价地最大化类间方差来选择最佳阈值。这种方法特别适用于图像的二值化处理,能够自动确定一个阈值,将图像中的像素分为黑色和白色两类。 Otsu 方法的原…...

Ascend NPU上适配Step-Audio模型
1 概述 1.1 简述 Step-Audio 是业界首个集语音理解与生成控制一体化的产品级开源实时语音对话系统,支持多语言对话(如 中文,英文,日语),语音情感(如 开心,悲伤)&#x…...

工业自动化时代的精准装配革新:迁移科技3D视觉系统如何重塑机器人定位装配
AI3D视觉的工业赋能者 迁移科技成立于2017年,作为行业领先的3D工业相机及视觉系统供应商,累计完成数亿元融资。其核心技术覆盖硬件设计、算法优化及软件集成,通过稳定、易用、高回报的AI3D视觉系统,为汽车、新能源、金属制造等行…...

实现弹窗随键盘上移居中
实现弹窗随键盘上移的核心思路 在Android中,可以通过监听键盘的显示和隐藏事件,动态调整弹窗的位置。关键点在于获取键盘高度,并计算剩余屏幕空间以重新定位弹窗。 // 在Activity或Fragment中设置键盘监听 val rootView findViewById<V…...

如何理解 IP 数据报中的 TTL?
目录 前言理解 前言 面试灵魂一问:说说对 IP 数据报中 TTL 的理解?我们都知道,IP 数据报由首部和数据两部分组成,首部又分为两部分:固定部分和可变部分,共占 20 字节,而即将讨论的 TTL 就位于首…...

什么是Ansible Jinja2
理解 Ansible Jinja2 模板 Ansible 是一款功能强大的开源自动化工具,可让您无缝地管理和配置系统。Ansible 的一大亮点是它使用 Jinja2 模板,允许您根据变量数据动态生成文件、配置设置和脚本。本文将向您介绍 Ansible 中的 Jinja2 模板,并通…...

初学 pytest 记录
安装 pip install pytest用例可以是函数也可以是类中的方法 def test_func():print()class TestAdd: # def __init__(self): 在 pytest 中不可以使用__init__方法 # self.cc 12345 pytest.mark.api def test_str(self):res add(1, 2)assert res 12def test_int(self):r…...

AI语音助手的Python实现
引言 语音助手(如小爱同学、Siri)通过语音识别、自然语言处理(NLP)和语音合成技术,为用户提供直观、高效的交互体验。随着人工智能的普及,Python开发者可以利用开源库和AI模型,快速构建自定义语音助手。本文由浅入深,详细介绍如何使用Python开发AI语音助手,涵盖基础功…...
