力扣-2663
题目
如果一个字符串满足以下条件,则称其为 美丽字符串 :
- 它由英语小写字母表的前
k个字母组成。 - 它不包含任何长度为
2或更长的回文子字符串。
给你一个长度为 n 的美丽字符串 s 和一个正整数 k 。
请你找出并返回一个长度为 n 的美丽字符串,该字符串还满足:在字典序大于 s 的所有美丽字符串中字典序最小。如果不存在这样的字符串,则返回一个空字符串。
对于长度相同的两个字符串 a 和 b ,如果字符串 a 在与字符串 b 不同的第一个位置上的字符字典序更大,则字符串 a 的字典序大于字符串 b 。
- 例如,
"abcd"的字典序比"abcc"更大,因为在不同的第一个位置(第四个字符)上d的字典序大于c。
示例 1:
输入:s = "abcz", k = 26 输出:"abda" 解释:字符串 "abda" 既是美丽字符串,又满足字典序大于 "abcz" 。 可以证明不存在字符串同时满足字典序大于 "abcz"、美丽字符串、字典序小于 "abda" 这三个条件。
示例 2:
输入:s = "dc", k = 4 输出:"" 解释:可以证明,不存在既是美丽字符串,又字典序大于 "dc" 的字符串。
思路
前提:如果字符串不包含任何长度为 2 和 3 的回文子字符串,则该字符串根本不包含任何回文子字符串。
题目简单来说就是在有限的字母范内给你一个没有回文子字符串的字符串,返回比这个字符串大的最小字符串,注意要在范围内,否则返回空字符串。
解题方法
由于原字符串已经是美丽字符串,所以我们只需要将最后一位加1,进行判断,首先看有没有超出字母范围,如果超出,赋最小的值a,进位,判断是否能进位,不能返归空字符串。再判断是否构成回文字符串,i>0&&str[i]==str[i-1]||i>1&&str[i]==str[i-2]是的话,数值加一,否则在i<n里判断后面是否构成回文字符串。构成就加1,不构成i++,每一次都会判断有没有超出字母范围,如果超出,赋最小的值a,进位。
代码
class Solution {public String smallestBeautifulString(String s, int k) {int n=s.length();k=k+'a';char[] str=s.toCharArray();int i=n-1;str[i]++;while(i<n){if(str[i]==k){if(i==0){return "";}str[i]='a';str[--i]++;}else if(i>0&&str[i]==str[i-1]||i>1&&str[i]==str[i-2]){str[i]++;}else{i++;}}return new String(str);}
}相关文章:

力扣-2663
题目 如果一个字符串满足以下条件,则称其为 美丽字符串 : 它由英语小写字母表的前 k 个字母组成。它不包含任何长度为 2 或更长的回文子字符串。 给你一个长度为 n 的美丽字符串 s 和一个正整数 k 。 请你找出并返回一个长度为 n 的美丽字符串&#…...

CausalMMM:基于因果结构学习的营销组合建模
1. 摘要 在线广告中,营销组合建模(Marketing Mix Modeling,MMM) 被用于预测广告商家的总商品交易量(GMV),并帮助决策者调整各种广告渠道的预算分配。传统的基于回归技术的MMM方法在复杂营销场景…...

编译 CUDA 程序的基本知识和步骤
基本工具 NVCC(NVIDIA CUDA Compiler): nvcc 是 NVIDIA 提供的 CUDA 编译器,用于将 CUDA 源代码(.cu 文件)编译成可执行文件或库。它可以处理 CUDA 和主机代码(例如 C)的混合编译。nvcc 调用底层…...
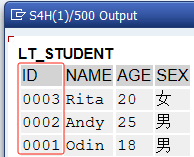
[SAP ABAP] 排序内表数据
语法格式 整表排序 SORT <itab> [ASCENDING|DESCENDING]. 按指定字段排序 SORT <itab> BY f1 [ASCENDING|DESCENDING] f2 [ASCENDING|DESCENDING] ... fn [ASCENDING|DESCENDING].<itab>:代表内表 不指定排序方式则默认升序排序 示例1 结果显…...

【UML用户指南】-21-对基本行为建模-活动图
目录 1、概念 2、组成结构 2.1、动作 2.2、活动节点 2.3、控制流 2.4、分支 2.5、分岔和汇合 2.6、泳道 2.7、对象流 2.8、扩展区域 3、一般用法 3.1、对工作流建模 3.2、对操作建模 一个活动图从本质上说是一个流程图,展现从活动到活动的控制流 活动图…...

【web2】jquary,bootstrap,vue
文章目录 1.jquary:选择器1.1 jquery框架引入:$("mydiv") 当成id选择器1.2 jquery版本/对象:$(js对象) -> jquery对象1.3 jquery的页面加载事件:$ 想象成 window.onload 1.4 jquery的基本选择器:$()里内容…...

独角兽品牌獭崎酱酒:高性价比的酱香之选
在酱香型白酒领域中,獭崎酱酒以其独特的品牌定位和高性价比迅速崛起,成为市场上备受关注的独角兽品牌。作为贵州茅台镇的一款新秀酱香酒,獭崎酱酒不仅传承了百年酿造工艺,还以创新的商业模式和亲民的价格赢得了广大消费者的青睐。…...

java打印菱形和空心菱形
java打印菱形 菱形分上下两个部分。其中上部分同打印金字塔;下部分循环部分i是递减 (ps:菱形层数只能为奇数) import java.util.Scanner;public class Lingxing{public static void main(String[] args) {Scanner myScanner new Scanner(S…...

Day10 —— 大数据技术之Scala
Scala编程入门 Scala的概述什么是Scala?Scala的重要特点Scala的使用场景 Scala的安装Scala基础Scala总结 Scala的概述 什么是Scala? Scala是一种将面向对象和函数式编程结合在一起的高级语言,旨在以简洁、优雅和类型安全的方式表达通用编程…...

Linux应用系统快速部署:docker快速部署linux应用程序
目录 一、背景 (一)引入docker的起因 (二)docker介绍 (三)Docker部署的优势 1、轻量级和可移植性 2、快速部署和扩展 3、一致性 4、版本控制 5、安全性 6、资源隔离 7、简化团队协作 8、多容器…...
?)
三目运算符中间的表达式可以省略吗(a?:c)?
熟悉C语言的童靴对三目运算符都非常熟悉,a? b : c; 如果a为true,则整个运算符的值为b,否则为c;那么问题来了,三目运算符中间的表达式可以省略吗?即a? : c; 1、linux内核中出现的省略情况 本人在阅读内核代码是发现了下面的代码: preferr…...

android 彩虹进度条自定义view实现
实现一个彩虹色进度条功能,不说明具体用途大家应该能猜到。想找别人造的轮子,但是没有合适的,所以决定自己实现一个。 相关知识 android 自定义view LinearGradient 线性渐变 实现步骤 自定义view 自定义一个TmcView类继承View 重写两…...
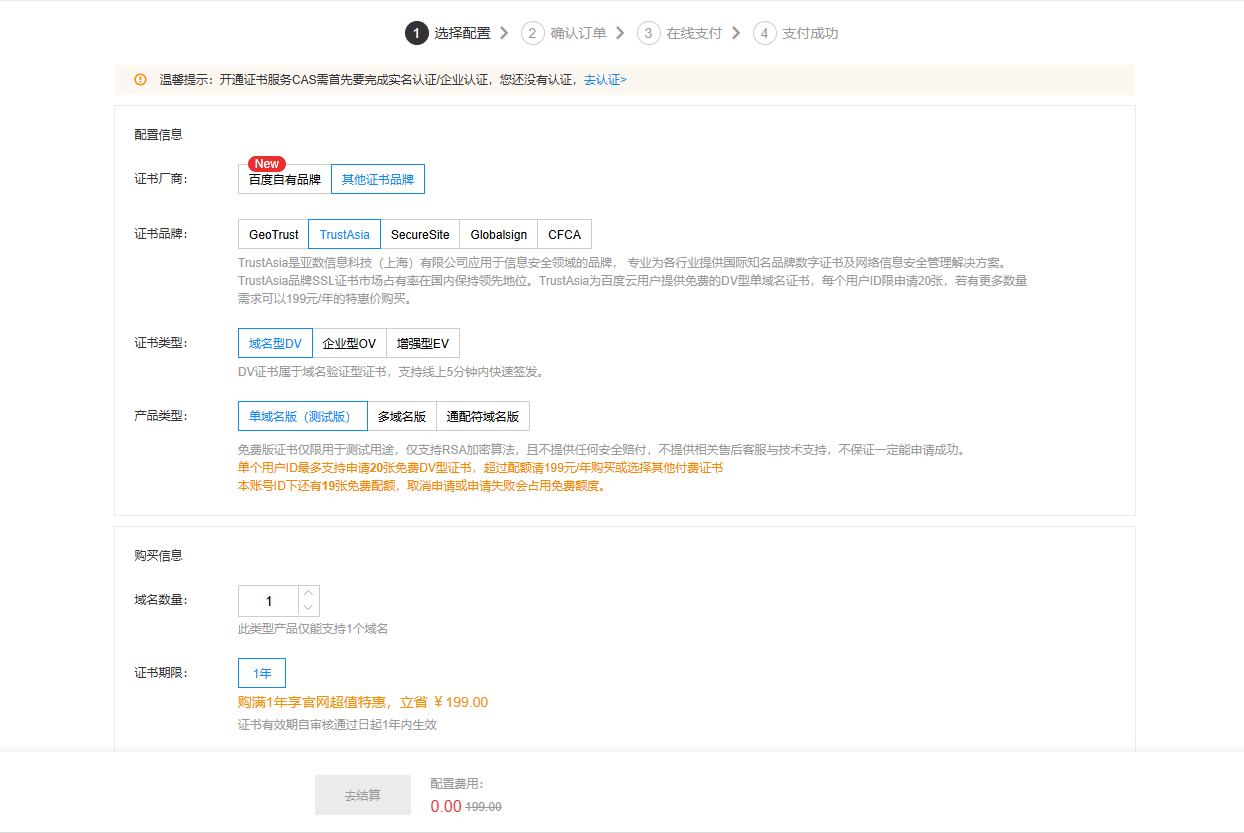
免费一年SSL证书申请——建议收藏
免费一年SSL证书申请——建议收藏 获取免费一年期SSL证书其实挺简单的 准备你的网站: 确保你的网站已经有了域名,而且这个域名已经指向你的服务器。还要检查你的服务器支持HTTPS,也就是443端口要打开,这是HTTPS默认用的。 验证域…...
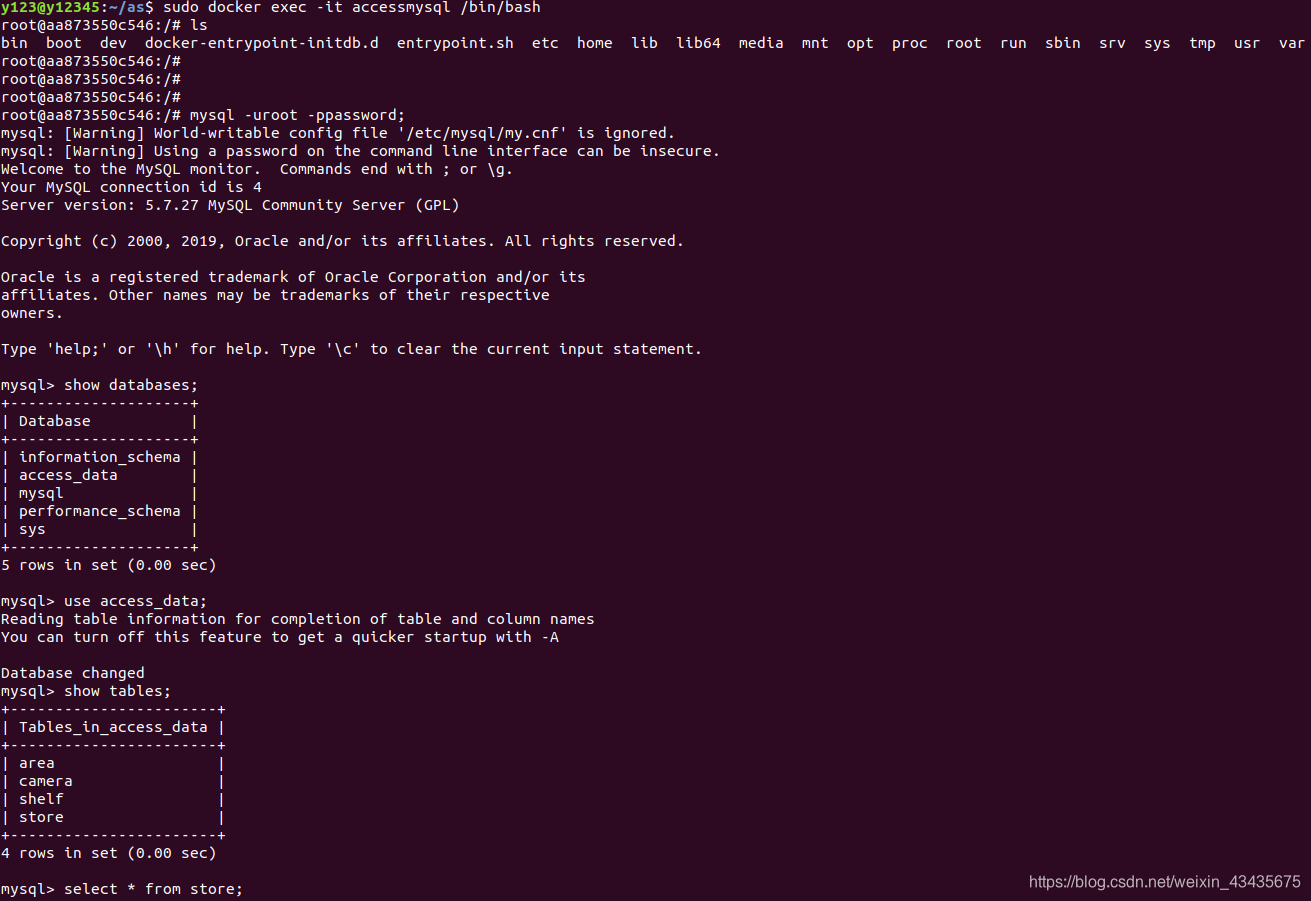
【docker1】指令,docker-compose,Dockerfile
文章目录 1.pull/image,run/ps(进程),exec/commit2.save/load:docker save 镜像id,不是容器id3.docker-compose:多容器:宿主机(eth0网卡)安装docker会生成一…...

Flutter中的异步和多进程
Flutter 是一个用于创建高性能、高保真度移动应用的框架,它使用 Dart 编程语言。 在 Flutter 中,异步和多进程是两种不同的概念,用于解决不同的问题。 异步 (Asynchronous) 异步编程是一种编程范式,允许代码在等待操作完成(如网络请求、文件 I/O)时继续执行其他任务,而不…...

学习C++第二天
1.缺省参数 缺省参数的概念: 缺省参数是声明或定义函数时为函数的参数指定一个缺省值。在调用该函数时,如果没有指定实参则采用该形参的缺省值,否则使用指定的实参。 void show(int a 10) {cout << a << endl; }int main() {sho…...

解析Java中1000个常用类:AbstractSet类,你学会了吗?
推荐一个我自己写的小报童专栏导航网站: http://xbt100.top 收录了生财有术项目精选、AI海外赚钱、纯银的产品分析等专栏,陆续会收录更多的专栏,欢迎体验~复制URL可直达。 以下是正文。 在 Java 集合框架中,AbstractSet 是一个重要的抽象类,为实现自定义的集合(Set)提…...

Nginx基础概念和常用操作
文章目录 1. 安装、启动、连接2. 快速尝试部署网站3. 配置文件1. nginx.conf全局配置事件模块HTTP 模块性能优化建议 2. default.confserver 块基本设置日志设置根路径设置 4. 反向代理1. 模拟3个Web2. 链接 5. 负载均衡1. 加权轮询,Weighted Round Robin2. 最少连接…...

圈复杂度是什么?go语言调整圈复杂度举例
圈复杂度(也称为循环复杂度或McCabe复杂度)是衡量程序复杂性的一个指标,它通常与代码中的控制流结构(如条件语句、循环和函数调用)的数量相关。在Go语言中,你可以通过重构代码来降低圈复杂度,从…...
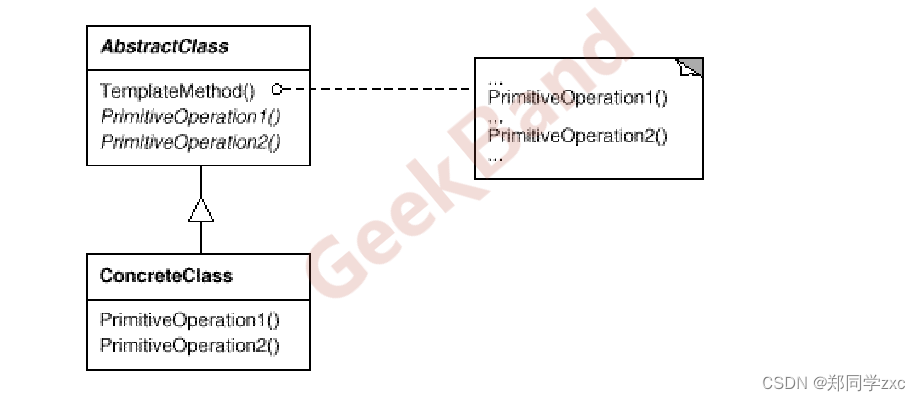
设计模式4-模版方法
设计模式 重构获得模式重构的关键技法1. 静态转动态2. 早绑定转晚绑定3. 继承转组合4. 编译时依赖转运行时依赖5. 紧耦合转松耦合 组件协助动机模式定义结构 要点总结。 例子示例解释: 重构获得模式 设计模式的目的是应对变化,提高复用 设计模式的要点…...

测试微信模版消息推送
进入“开发接口管理”--“公众平台测试账号”,无需申请公众账号、可在测试账号中体验并测试微信公众平台所有高级接口。 获取access_token: 自定义模版消息: 关注测试号:扫二维码关注测试号。 发送模版消息: import requests da…...

多模态2025:技术路线“神仙打架”,视频生成冲上云霄
文|魏琳华 编|王一粟 一场大会,聚集了中国多模态大模型的“半壁江山”。 智源大会2025为期两天的论坛中,汇集了学界、创业公司和大厂等三方的热门选手,关于多模态的集中讨论达到了前所未有的热度。其中,…...

简易版抽奖活动的设计技术方案
1.前言 本技术方案旨在设计一套完整且可靠的抽奖活动逻辑,确保抽奖活动能够公平、公正、公开地进行,同时满足高并发访问、数据安全存储与高效处理等需求,为用户提供流畅的抽奖体验,助力业务顺利开展。本方案将涵盖抽奖活动的整体架构设计、核心流程逻辑、关键功能实现以及…...

2024年赣州旅游投资集团社会招聘笔试真
2024年赣州旅游投资集团社会招聘笔试真 题 ( 满 分 1 0 0 分 时 间 1 2 0 分 钟 ) 一、单选题(每题只有一个正确答案,答错、不答或多答均不得分) 1.纪要的特点不包括()。 A.概括重点 B.指导传达 C. 客观纪实 D.有言必录 【答案】: D 2.1864年,()预言了电磁波的存在,并指出…...

JVM垃圾回收机制全解析
Java虚拟机(JVM)中的垃圾收集器(Garbage Collector,简称GC)是用于自动管理内存的机制。它负责识别和清除不再被程序使用的对象,从而释放内存空间,避免内存泄漏和内存溢出等问题。垃圾收集器在Ja…...

多模态商品数据接口:融合图像、语音与文字的下一代商品详情体验
一、多模态商品数据接口的技术架构 (一)多模态数据融合引擎 跨模态语义对齐 通过Transformer架构实现图像、语音、文字的语义关联。例如,当用户上传一张“蓝色连衣裙”的图片时,接口可自动提取图像中的颜色(RGB值&…...

linux 错误码总结
1,错误码的概念与作用 在Linux系统中,错误码是系统调用或库函数在执行失败时返回的特定数值,用于指示具体的错误类型。这些错误码通过全局变量errno来存储和传递,errno由操作系统维护,保存最近一次发生的错误信息。值得注意的是,errno的值在每次系统调用或函数调用失败时…...

Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决
Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决 问题背景 在一个基于 Spring Cloud Gateway WebFlux 构建的微服务项目中,新增了一个本地验证码接口 /code,使用函数式路由(RouterFunction)和 Hutool 的 Circle…...

MySQL 8.0 事务全面讲解
以下是一个结合两次回答的 MySQL 8.0 事务全面讲解,涵盖了事务的核心概念、操作示例、失败回滚、隔离级别、事务性 DDL 和 XA 事务等内容,并修正了查看隔离级别的命令。 MySQL 8.0 事务全面讲解 一、事务的核心概念(ACID) 事务是…...

解析两阶段提交与三阶段提交的核心差异及MySQL实现方案
引言 在分布式系统的事务处理中,如何保障跨节点数据操作的一致性始终是核心挑战。经典的两阶段提交协议(2PC)通过准备阶段与提交阶段的协调机制,以同步决策模式确保事务原子性。其改进版本三阶段提交协议(3PC…...
