三目运算符中间的表达式可以省略吗(a?:c)?
熟悉C语言的童靴对三目运算符都非常熟悉,a? b : c; 如果a为true,则整个运算符的值为b,否则为c;那么问题来了,三目运算符中间的表达式可以省略吗?即a? : c;
1、linux内核中出现的省略情况
本人在阅读内核代码是发现了下面的代码:
preferred_zoneref = first_zones_zonelist(ac.zonelist, ac.high_zoneidx,
ac.nodemask ? : &cpuset_current_mems_allowed,&ac.preferred_zone);
其中标红部分是一个三目运算符,而且还是一个省略的三目运算符。那么问题来了,a? : c如果a为true的情况下,整个三目运算符的值到底是什么?
2、动手测试下
#include <stdio.h>
#include <stdlib.h>
int bar(char *a,char*b)
{
if(a != NULL)
printf("%s \r\n",a);
else
printf("a is NULL \r\n");
if(b != NULL)
printf("%s \r\n",b);
else
printf("b is NULL \r\n");
return 0;
}
int main(int argc,char *argv[])
{
char *a = "hello";
char *b = "world";
char *c = "how are you?";
bar(a,b);
printf("%s \r\n",c?"no NULL":"NULL");
bar(a,c? : "i am fine");
return 0;
}
输出结果如下:
hello
world
no NULL
hello
how are you?
c? : "i am fine" 的运算结果是"how are you?",即变量c初始化的值。
所以可知,三目运算符(a?b:c)出现省略的情况下(a?:c),省略值就是第一个运算符a的值。
如果将c省略,即a?b: ;测试发现编译会报错。
相关文章:
?)
三目运算符中间的表达式可以省略吗(a?:c)?
熟悉C语言的童靴对三目运算符都非常熟悉,a? b : c; 如果a为true,则整个运算符的值为b,否则为c;那么问题来了,三目运算符中间的表达式可以省略吗?即a? : c; 1、linux内核中出现的省略情况 本人在阅读内核代码是发现了下面的代码: preferr…...

android 彩虹进度条自定义view实现
实现一个彩虹色进度条功能,不说明具体用途大家应该能猜到。想找别人造的轮子,但是没有合适的,所以决定自己实现一个。 相关知识 android 自定义view LinearGradient 线性渐变 实现步骤 自定义view 自定义一个TmcView类继承View 重写两…...
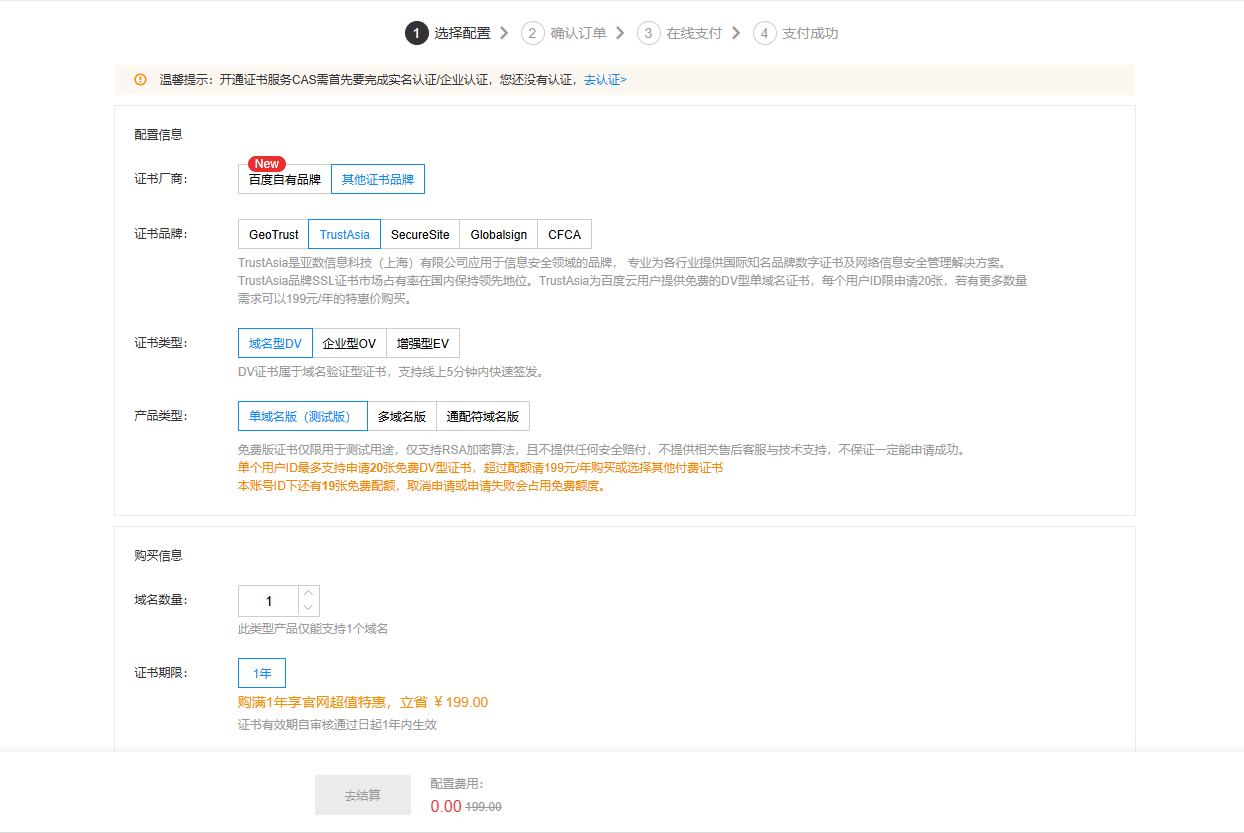
免费一年SSL证书申请——建议收藏
免费一年SSL证书申请——建议收藏 获取免费一年期SSL证书其实挺简单的 准备你的网站: 确保你的网站已经有了域名,而且这个域名已经指向你的服务器。还要检查你的服务器支持HTTPS,也就是443端口要打开,这是HTTPS默认用的。 验证域…...
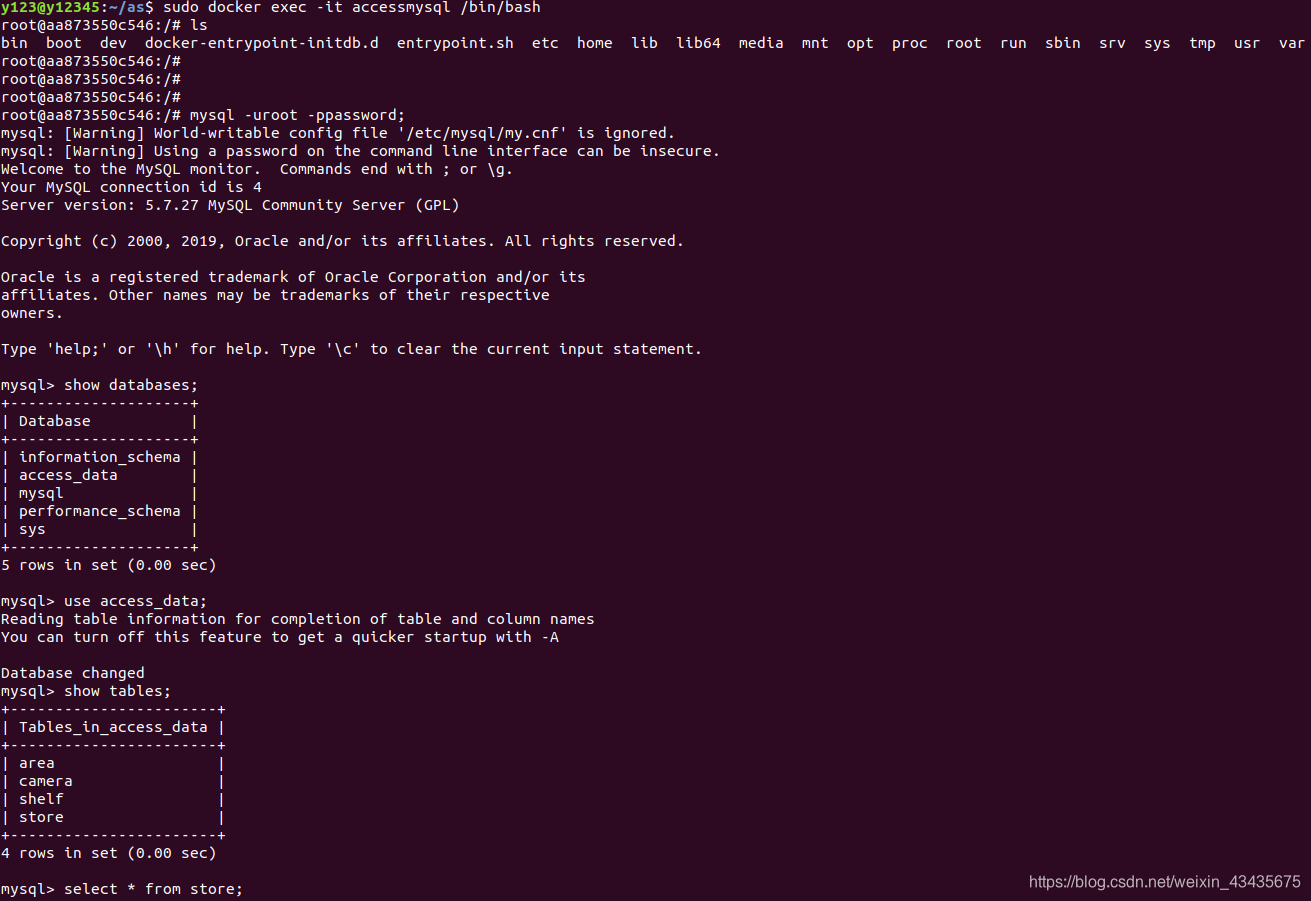
【docker1】指令,docker-compose,Dockerfile
文章目录 1.pull/image,run/ps(进程),exec/commit2.save/load:docker save 镜像id,不是容器id3.docker-compose:多容器:宿主机(eth0网卡)安装docker会生成一…...

Flutter中的异步和多进程
Flutter 是一个用于创建高性能、高保真度移动应用的框架,它使用 Dart 编程语言。 在 Flutter 中,异步和多进程是两种不同的概念,用于解决不同的问题。 异步 (Asynchronous) 异步编程是一种编程范式,允许代码在等待操作完成(如网络请求、文件 I/O)时继续执行其他任务,而不…...

学习C++第二天
1.缺省参数 缺省参数的概念: 缺省参数是声明或定义函数时为函数的参数指定一个缺省值。在调用该函数时,如果没有指定实参则采用该形参的缺省值,否则使用指定的实参。 void show(int a 10) {cout << a << endl; }int main() {sho…...

解析Java中1000个常用类:AbstractSet类,你学会了吗?
推荐一个我自己写的小报童专栏导航网站: http://xbt100.top 收录了生财有术项目精选、AI海外赚钱、纯银的产品分析等专栏,陆续会收录更多的专栏,欢迎体验~复制URL可直达。 以下是正文。 在 Java 集合框架中,AbstractSet 是一个重要的抽象类,为实现自定义的集合(Set)提…...

Nginx基础概念和常用操作
文章目录 1. 安装、启动、连接2. 快速尝试部署网站3. 配置文件1. nginx.conf全局配置事件模块HTTP 模块性能优化建议 2. default.confserver 块基本设置日志设置根路径设置 4. 反向代理1. 模拟3个Web2. 链接 5. 负载均衡1. 加权轮询,Weighted Round Robin2. 最少连接…...

圈复杂度是什么?go语言调整圈复杂度举例
圈复杂度(也称为循环复杂度或McCabe复杂度)是衡量程序复杂性的一个指标,它通常与代码中的控制流结构(如条件语句、循环和函数调用)的数量相关。在Go语言中,你可以通过重构代码来降低圈复杂度,从…...
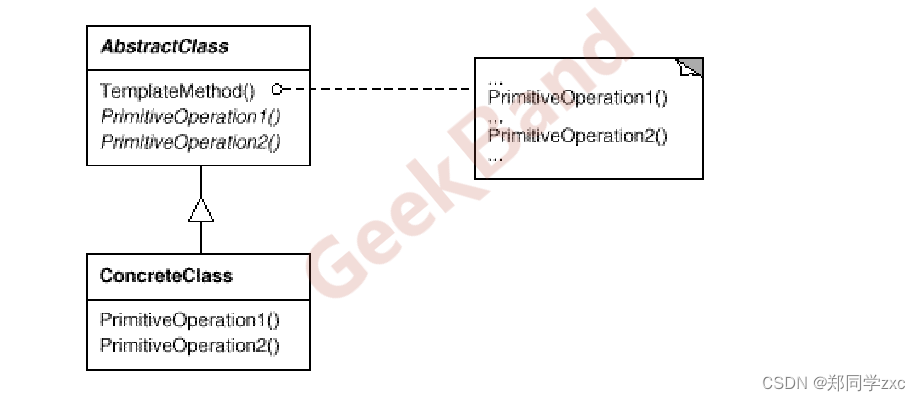
设计模式4-模版方法
设计模式 重构获得模式重构的关键技法1. 静态转动态2. 早绑定转晚绑定3. 继承转组合4. 编译时依赖转运行时依赖5. 紧耦合转松耦合 组件协助动机模式定义结构 要点总结。 例子示例解释: 重构获得模式 设计模式的目的是应对变化,提高复用 设计模式的要点…...
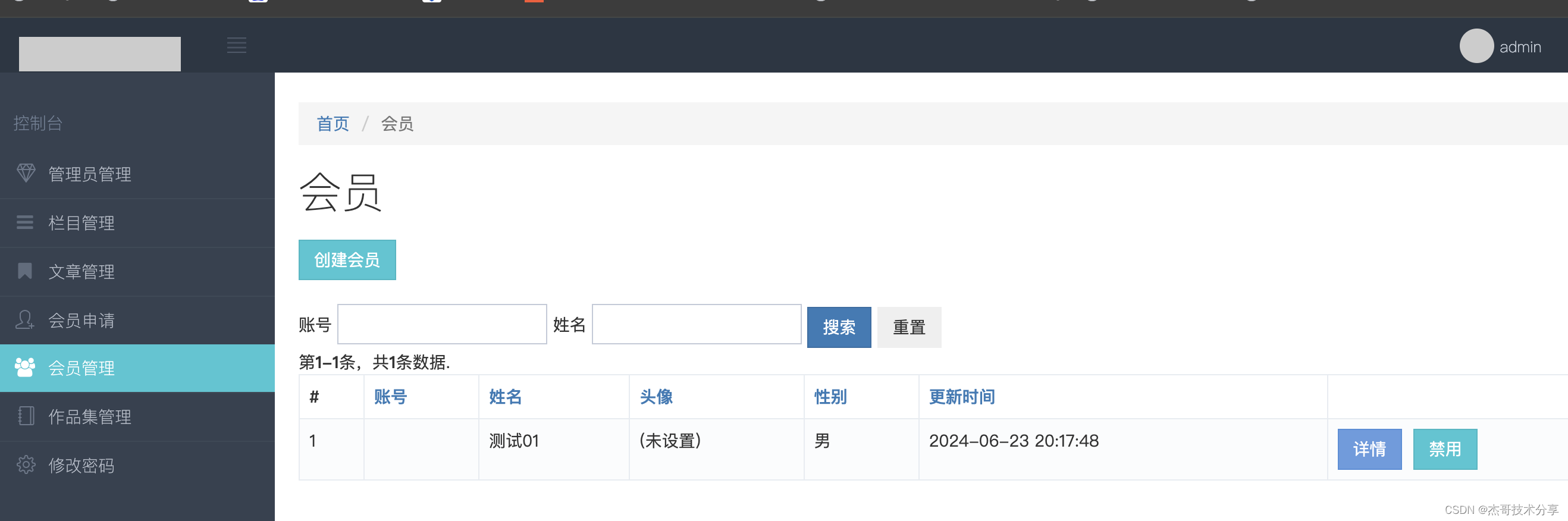
yii2 ActiveForm使用技巧
持续更新: 1、搜索输入框:form-inline <?php $form ActiveForm::begin([action > [index],method > get,options > [class > form-inline] (增加此行代码) ]); ?>...

【面试】基本数据类型的包装类缓存
目录 1. 说明2. Integer类分析2.1 代码块2.2 字节码2.3 分析2.4 valueOf方法 1. 说明 1.在java中,基本数据类型的包装类(Integer、Byte、Character、Short、Long、Boolean)的某些值会被缓存。2.以提高性能并减少内存使用。3.这种缓存机制是自…...
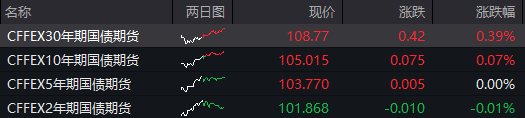
6月20日(周四)A股行情总结:A股险守3000点,恒生科技指数跌1.6%
A股三大股指走弱,科创板逆势上扬,半导体板块走强,多股20CM涨停。中芯国际港股涨超1%。恒生科技指数跌超1%。离岸人民币对美元汇率小幅走低,20日盘中最低跌至7.2874,创下2023年11月中旬以来的新低,随后收复部…...
Parallels Desktop 19 for mac破解版安装激活使用指南
Parallels Desktop 19 for Mac 乃是一款适配于 Mac 的虚拟化软件。它能让您在 Mac 计算机上同时运行多个操作系统。您可借此创建虚拟机,并于其中装设不同的操作系统,如 Windows、Linux 或 macOS。使用 Parallels Desktop 19 mac 版时,您可在 …...

JExcel API使用笔记
JExcel API使用笔记 JExcel是一个开源的支持excel的java类库,广泛利用其api来生成excel报表 API基本使用 1.创建excel文件 workbook Workbook.createWorkbook(file);//传入file文件2.创建sheet页 WritableSheet sheet workbook.createSheet("记录表&quo…...
springCloudAlibaba之分布式网关组件---gateway
gateway-网关 网关spring cloud gatewaygateway初体验gateway整合nacos简写方式 内置路由断言工厂内置断言工厂 自定义路由断言工厂自定义路由工厂 内置/自定义过滤器典型内置过滤器自定义过滤器 全局过滤器自定义全局过滤器 请求日志记录&跨域处理Gateway跨域配置…...

Springboot项目jar加密
部署的程序进行加密,防止第三方非法拷贝走项目进行二次开发或部署。我们知道java代码编译后生成的以.class结尾的字节码文件或者.jar/.war结尾的可执行文件都是可以反编译生成.java文件的,虽然反编译后生成的.java文件和原本的.java文件有些微差别&#…...

【React】高阶组件
概述 高阶组件并非一个组件,而是增强组件功能的一个函数。 高阶组件的作用是对多个组件公共逻辑进行横向抽离。 高阶组件 – React (reactjs.org) 示例 ChildCom1.jsx import React from react;function ChildCom1(props) {return (<div>这是子组件1<d…...

全面理解-Flutter(万字长文,深度解析)
1、Web 性能差,跟原生 App 存在肉眼可见的差距; 2、React Native 跟 Web 相比,支持的能力非常有限,特定长场景问题,需要三端团队一个一个处理; 3、Web 浏览器的安卓碎片化严重(感谢 X5&#x…...

RabbitMQ实战宝典:从新手到专家的全面探索
前言 在当今分布式系统架构中,消息队列已成为不可或缺的一部分,而RabbitMQ作为其中的佼佼者,凭借其强大的功能和灵活性,广泛应用于各种规模的应用场景中。本文将带你从基础概念出发,深入探讨RabbitMQ的核心特性&#…...

以下是对华为 HarmonyOS NETX 5属性动画(ArkTS)文档的结构化整理,通过层级标题、表格和代码块提升可读性:
一、属性动画概述NETX 作用:实现组件通用属性的渐变过渡效果,提升用户体验。支持属性:width、height、backgroundColor、opacity、scale、rotate、translate等。注意事项: 布局类属性(如宽高)变化时&#…...

基于服务器使用 apt 安装、配置 Nginx
🧾 一、查看可安装的 Nginx 版本 首先,你可以运行以下命令查看可用版本: apt-cache madison nginx-core输出示例: nginx-core | 1.18.0-6ubuntu14.6 | http://archive.ubuntu.com/ubuntu focal-updates/main amd64 Packages ng…...

高频面试之3Zookeeper
高频面试之3Zookeeper 文章目录 高频面试之3Zookeeper3.1 常用命令3.2 选举机制3.3 Zookeeper符合法则中哪两个?3.4 Zookeeper脑裂3.5 Zookeeper用来干嘛了 3.1 常用命令 ls、get、create、delete、deleteall3.2 选举机制 半数机制(过半机制࿰…...

第一篇:Agent2Agent (A2A) 协议——协作式人工智能的黎明
AI 领域的快速发展正在催生一个新时代,智能代理(agents)不再是孤立的个体,而是能够像一个数字团队一样协作。然而,当前 AI 生态系统的碎片化阻碍了这一愿景的实现,导致了“AI 巴别塔问题”——不同代理之间…...

unix/linux,sudo,其发展历程详细时间线、由来、历史背景
sudo 的诞生和演化,本身就是一部 Unix/Linux 系统管理哲学变迁的微缩史。来,让我们拨开时间的迷雾,一同探寻 sudo 那波澜壮阔(也颇为实用主义)的发展历程。 历史背景:su的时代与困境 ( 20 世纪 70 年代 - 80 年代初) 在 sudo 出现之前,Unix 系统管理员和需要特权操作的…...

tree 树组件大数据卡顿问题优化
问题背景 项目中有用到树组件用来做文件目录,但是由于这个树组件的节点越来越多,导致页面在滚动这个树组件的时候浏览器就很容易卡死。这种问题基本上都是因为dom节点太多,导致的浏览器卡顿,这里很明显就需要用到虚拟列表的技术&…...

rnn判断string中第一次出现a的下标
# coding:utf8 import torch import torch.nn as nn import numpy as np import random import json""" 基于pytorch的网络编写 实现一个RNN网络完成多分类任务 判断字符 a 第一次出现在字符串中的位置 """class TorchModel(nn.Module):def __in…...

Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习)
Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习) 一、Aspose.PDF 简介二、说明(⚠️仅供学习与研究使用)三、技术流程总览四、准备工作1. 下载 Jar 包2. Maven 项目依赖配置 五、字节码修改实现代码&#…...

Linux系统部署KES
1、安装准备 1.版本说明V008R006C009B0014 V008:是version产品的大版本。 R006:是release产品特性版本。 C009:是通用版 B0014:是build开发过程中的构建版本2.硬件要求 #安全版和企业版 内存:1GB 以上 硬盘…...

沙箱虚拟化技术虚拟机容器之间的关系详解
问题 沙箱、虚拟化、容器三者分开一一介绍的话我知道他们各自都是什么东西,但是如果把三者放在一起,它们之间到底什么关系?又有什么联系呢?我不是很明白!!! 就比如说: 沙箱&#…...
