图文详解红黑树,还有谁不会?
前言
在MySQL中,无论是Innodb还是MyIsam,都使用了B+树作索引结构(这里不考虑hash等其他索引)。本文将从最普通的二叉查找树开始,逐步说明各种树解决的问题以及面临的新问题,从而说明MySQL为什么选择B+树作为索引结构。
目录
一、二叉查找树(BST):不平衡
二、平衡二叉树(AVL):旋转耗时
三、红黑树:树太高
四、B树:为磁盘而生
五、B+树
六、感受B+树的威力
七、总结
一、二叉查找树(BST):不平衡
二叉查找树(BST,Binary Search Tree),也叫二叉排序树,在二叉树的基础上需要满足:任意节点的左子树上所有节点值不大于根节点的值,任意节点的右子树上所有节点值不小于根节点的值。如下是一颗BST(图片来源)。
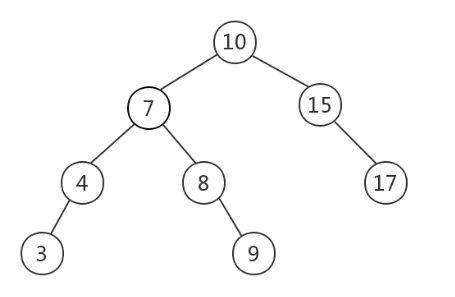
当需要快速查找时,将数据存储在BST是一种常见的选择,因为此时查询时间取决于树高,平均时间复杂度是O(lgn)。然而BST可能长歪而变得不平衡,如下图所示(图片来源),此时BST退化为链表,时间复杂度退化为O(n)。
为了解决这个问题,引入了平衡二叉树。

二、平衡二叉树(AVL):旋转耗时
AVL树是严格的平衡二叉树,所有节点的左右子树高度差不能超过1;AVL树查找、插入和删除在平均和最坏情况下都是O(lgn)。
AVL实现平衡的关键在于旋转操作:插入和删除可能破坏二叉树的平衡,此时需要通过一次或多次树旋转来重新平衡这个树。当插入数据时,最多只需要1次旋转(单旋转或双旋转);但是当删除数据时,会导致树失衡,AVL需要维护从被删除节点到根节点这条路径上所有节点的平衡,旋转的量级为O(lgn)。
由于旋转的耗时,AVL树在删除数据时效率很低;在删除操作较多时,维护平衡所需的代价可能高于其带来的好处,因此AVL实际使用并不广泛。另外,最新 Java 和数据结构面试题整理好了,点击Java面试库小程序在线刷题。
三、红黑树:树太高
与AVL树相比,红黑树并不追求严格的平衡,而是大致的平衡:只是确保从根到叶子的最长的可能路径不多于最短的可能路径的两倍长。从实现来看,红黑树最大的特点是每个节点都属于两种颜色(红色或黑色)之一,且节点颜色的划分需要满足特定的规则(具体规则略)。红黑树示例如下(图片来源):
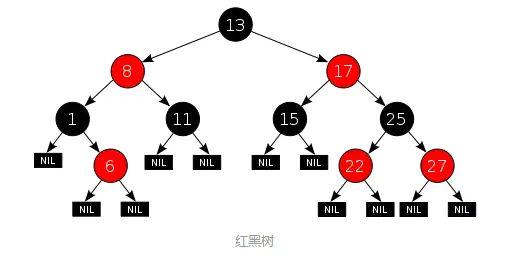
与AVL树相比,红黑树的查询效率会有所下降,这是因为树的平衡性变差,高度更高。但红黑树的删除效率大大提高了,因为红黑树同时引入了颜色,当插入或删除数据时,只需要进行O(1)次数的旋转以及变色就能保证基本的平衡,不需要像AVL树进行O(lgn)次数的旋转。总的来说,红黑树的统计性能高于AVL。
因此,在实际应用中,AVL树的使用相对较少,而红黑树的使用非常广泛。例如,Java中的TreeMap使用红黑树存储排序键值对;Java8中的HashMap使用链表+红黑树解决哈希冲突问题(当冲突节点较少时,使用链表,当冲突节点较多时,使用红黑树)。
对于数据在内存中的情况(如上述的TreeMap和HashMap),红黑树的表现是非常优异的。但是对于数据在磁盘等辅助存储设备中的情况(如MySQL等数据库),红黑树并不擅长,因为红黑树长得还是太高了。当数据在磁盘中时,磁盘IO会成为最大的性能瓶颈,设计的目标应该是尽量减少IO次数;而树的高度越高,增删改查所需要的IO次数也越多,会严重影响性能。
四、B树:为磁盘而生
B树也称B-树(其中-不是减号),是为磁盘等辅存设备设计的多路平衡查找树,与二叉树相比,B树的每个非叶节点可以有多个子树。 因此,当总节点数量相同时,B树的高度远远小于AVL树和红黑树(B树是一颗“矮胖子”),磁盘IO次数大大减少。
定义B树最重要的概念是阶数(Order),对于一颗m阶B树,需要满足以下条件:
每个节点最多包含 m 个子节点。
如果根节点包含子节点,则至少包含 2 个子节点;除根节点外,每个非叶节点至少包含 m/2 个子节点。
拥有 k 个子节点的非叶节点将包含 k - 1 条记录。
所有叶节点都在同一层中。
可以看出,B树的定义,主要是对非叶结点的子节点数量和记录数量的限制
下图是一个3阶B树的例子(图片来源):
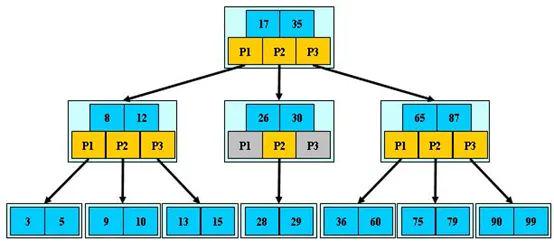
B树的优势除了树高小,还有对访问局部性原理的利用。所谓局部性原理,是指当一个数据被使用时,其附近的数据有较大概率在短时间内被使用。B树将键相近的数据存储在同一个节点,当访问其中某个数据时,数据库会将该整个节点读到缓存中;当它临近的数据紧接着被访问时,可以直接在缓存中读取,无需进行磁盘IO;换句话说,B树的缓存命中率更高。
B树在数据库中有一些应用,如mongodb的索引使用了B树结构。但是在很多数据库应用中,使用了是B树的变种B+树。
五、B+树
B+树也是多路平衡查找树,其与B树的区别主要在于:
B树中每个节点(包括叶节点和非叶节点)都存储真实的数据,B+树中只有叶子节点存储真实的数据,非叶节点只存储键。在MySQL中,这里所说的真实数据,可能是行的全部数据(如Innodb的聚簇索引),也可能只是行的主键(如Innodb的辅助索引),或者是行所在的地址(如MyIsam的非聚簇索引)。
B树中一条记录只会出现一次,不会重复出现,而B+树的键则可能重复重现——一定会在叶节点出现,也可能在非叶节点重复出现。
B+树的叶节点之间通过双向链表链接。
B树中的非叶节点,记录数比子节点个数少1;而B+树中记录数与子节点个数相同。
由此,B+树与B树相比,有以下优势:
更少的IO次数:B+树的非叶节点只包含键,而不包含真实数据,因此每个节点存储的记录个数比B数多很多(即阶m更大),因此B+树的高度更低,访问时所需要的IO次数更少。此外,由于每个节点存储的记录数更多,所以对访问局部性原理的利用更好,缓存命中率更高。
更适于范围查询:在B树中进行范围查询时,首先找到要查找的下限,然后对B树进行中序遍历,直到找到查找的上限;而B+树的范围查询,只需要对链表进行遍历即可。
更稳定的查询效率:B树的查询时间复杂度在1到树高之间(分别对应记录在根节点和叶节点),而B+树的查询复杂度则稳定为树高,因为所有数据都在叶节点。
B+树也存在劣势:由于键会重复出现,因此会占用更多的空间。但是与带来的性能优势相比,空间劣势往往可以接受,因此B+树的在数据库中的使用比B树更加广泛。
六、感受B+树的威力
前面说到,B树/B+树与红黑树等二叉树相比,最大的优势在于树高更小。实际上,对于Innodb的B+索引来说,树的高度一般在2-4层。下面来进行一些具体的估算。
树的高度是由阶数决定的,阶数越大树越矮;而阶数的大小又取决于每个节点可以存储多少条记录。Innodb中每个节点使用一个页(page),页的大小为16KB,其中元数据只占大约128字节左右(包括文件管理头信息、页面头信息等等),大多数空间都用来存储数据。
对于非叶节点,记录只包含索引的键和指向下一层节点的指针。假设每个非叶节点页面存储1000条记录,则每条记录大约占用16字节;当索引是整型或较短的字符串时,这个假设是合理的。延伸一下,我们经常听到建议说索引列长度不应过大,原因就在这里:索引列太长,每个节点包含的记录数太少,会导致树太高,索引的效果会大打折扣,而且索引还会浪费更多的空间。
对于叶节点,记录包含了索引的键和值(值可能是行的主键、一行完整数据等,具体见前文),数据量更大。这里假设每个叶节点页面存储100条记录(实际上,当索引为聚簇索引时,这个数字可能不足100;当索引为辅助索引时,这个数字可能远大于100;可以根据实际情况进行估算)。
对于一颗3层B+树,第一层(根节点)有1个页面,可以存储1000条记录;第二层有1000个页面,可以存储10001000条记录;第三层(叶节点)有10001000个页面,每个页面可以存储100条记录,因此可以存储10001000100条记录,即1亿条。而对于二叉树,存储1亿条记录则需要26层左右。
七、总结
最后,总结一下各种树解决的问题以及面临的新问题:
二叉查找树(BST):解决了排序的基本问题,但是由于无法保证平衡,可能退化为链表;
平衡二叉树(AVL):通过旋转解决了平衡的问题,但是旋转操作效率太低;
红黑树:通过舍弃严格的平衡和引入红黑节点,解决了AVL旋转效率过低的问题,但是在磁盘等场景下,树仍然太高,IO次数太多;
B树:通过将二叉树改为多路平衡查找树,解决了树过高的问题;
B+树:在B树的基础上,将非叶节点改造为不存储数据的纯索引节点,进一步降低了树的高度;此外将叶节点使用指针连接成链表,范围查询更加高效。
相关文章:

图文详解红黑树,还有谁不会?
前言在MySQL中,无论是Innodb还是MyIsam,都使用了B树作索引结构(这里不考虑hash等其他索引)。本文将从最普通的二叉查找树开始,逐步说明各种树解决的问题以及面临的新问题,从而说明MySQL为什么选择B树作为索引结构。目录一、二叉查…...
多目标遗传算法NSGA-II原理详解及算法实现
在接触学习多目标优化的问题上,经常会被提及到多目标遗传算法NSGA-II,网上也看到了很多人对该算法的总结,但真正讲解明白的以及配套用算法实现的文章很少,这里也对该算法进行一次详解与总结。会有侧重点的阐述,不会针对…...

Spark 键值对RDD的操作
键值对RDD(Pair RDD)是指每个RDD元素都是(key,value)键值对类型,是一种常见的RDD类型,可以应用于很多的应用场景。 一、 键值对RDD的创建 键值对RDD的创建主要有两种方式: &#x…...
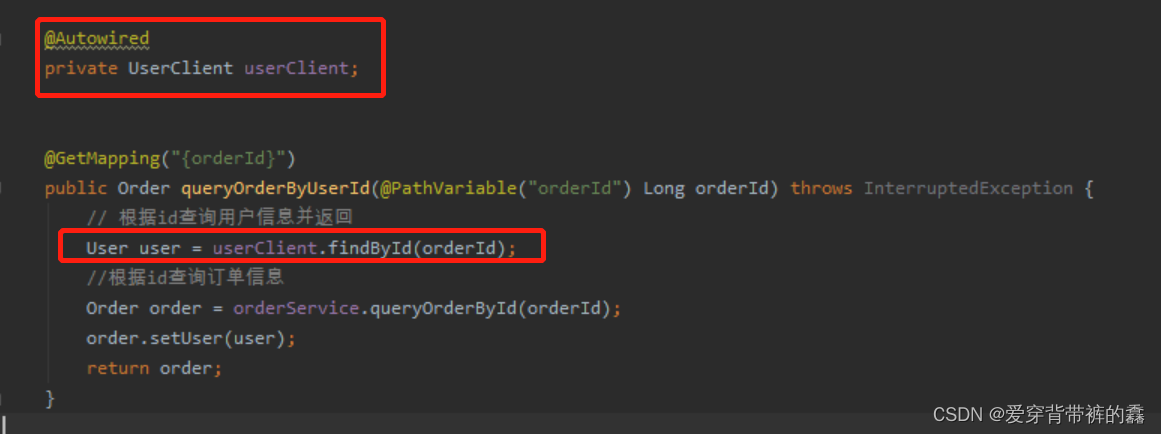
【SpringCloud】SpringCloud详解之Feign远程调用
目录前言SpringCloud Feign远程服务调用一.需求二.两个服务的yml配置和访问路径三.使用RestTemplate远程调用(order服务内编写)四.构建Feign(order服务内配置)五.自定义Feign配置(order服务内配置)六.Feign配置日志(oder服务内配置)七.Feign调优(order服务内配置)八.抽离Feign前…...
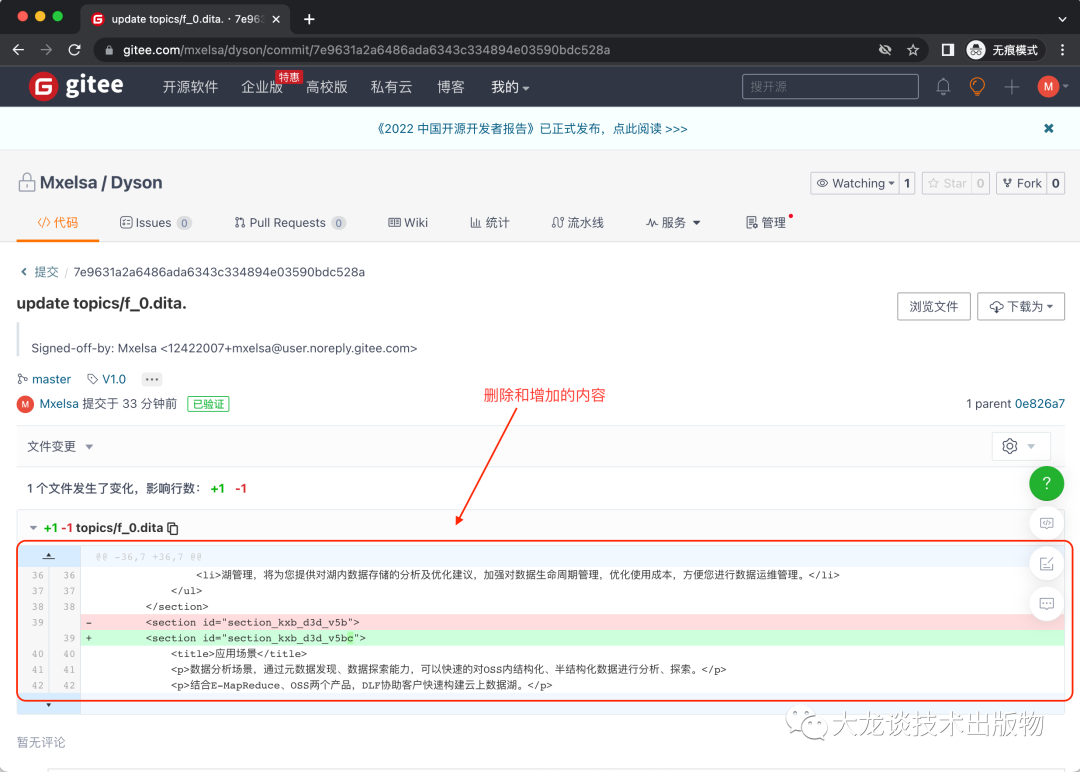
文档团队怎样使用GIT做版本管理
有不少小型文档团队想转结构化写作和发布,但是因为有限的IT技能和IT资源而受阻。本文为这样的小型文档团队而准备,描述怎样使用Git做内容的版本管理。 - 1 - 为什么需要版本管理 当一个团队进行协同创作内容时,有以下需要: 在对…...

【java】Java中-> 是什么意思?
先看一个例子 EventQueue.invokeLater(() -> {JFrame frame new ImageViewerFrame();frame.setTitle("ImageViewer");frame.setDefaultCloseOperation(JFrame.EXIT_ON_CLOSE);frame.setVisible(true);}); // 上面那一段可以看成如下: EventQueue.invokeLater(ne…...
网络类型部分实验
1.实验思路: 首先用DHCP 给四台PC配置上地址,配置成功后 其次底层IP地址的下发完成的同时,进行检测是否可以ping通 接着进行R1和R5之间使用PPP的PAP认证,R5为主认证方 主认证方ISP 被认证方R1 其次进行R2和R5使用PPP的CHAP认证&am…...
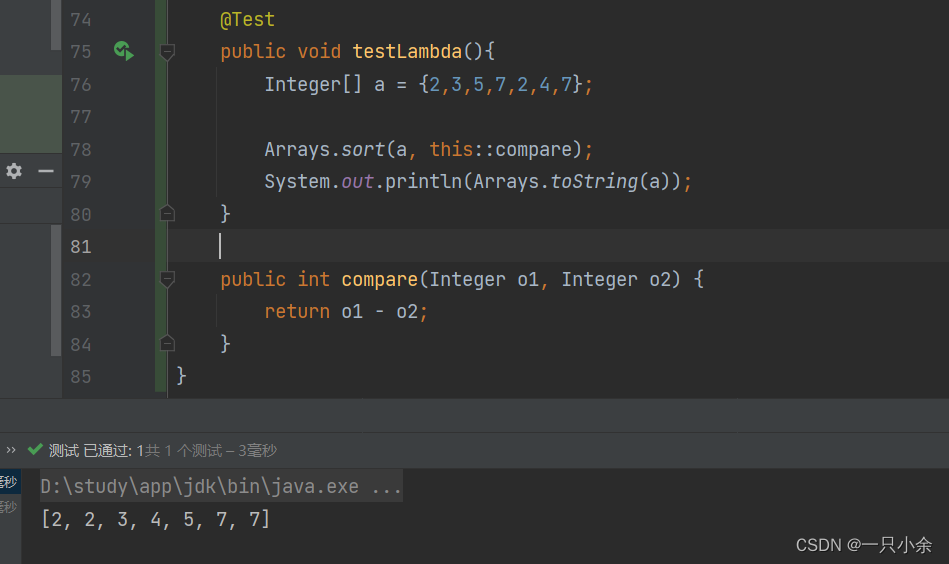
java教程--函数式接口--lambda表达式--方法引用
函数式接口 介绍 jdk8新特性,只有一个抽象方法的接口我们称之为函数接口。 FunctionalInterface JDK的函数式接口都加上了FunctionalInterface 注解进行标识。但是无论是否加上该注解只要接口中只有一个抽象方法,都是函数式接口。 如在Comparato…...
java——代理
什么是代理: 给目标对象一个代理对象,由代理对象控制着对目标对象的引用 为什么使用代理: ①:功能增强:通过代理业务对原有业务进行增强 ②:用户只能同行过代理对象间接访问目标对象,防止用…...

kubernetes中service探讨
文章目录序言kube-proxy代理模型userspace代理模型iptables代理模型ipvs代理模型修改代理模型Service资源类型ClusterIPNodePortLoadBalancerExternalName应用Service资源应用ClusterIP Service资源应用NodePort Service资源应用LoadBalancer Service资源外部IP序言 在Kuberne…...

Python3实现“美颜”功能
导语利用Python实现美颜。。。这是之前在GitHub上下载的一个项目。。。似乎有些日子了。。。所以暂时找不到原项目的链接了。。。今天抽空看了下它源代码的主要思想,似乎挺简单的。。。于是决定用Python3自己复现一下。。。T_T感觉还是挺有趣的。。。Just have a tr…...
【创建“待选项”按钮02计算坐标 Objective-C语言】
一、之前,我们已经把“待选项”按钮,创建好了,但是唯一的问题是,坐标都是一样的,所以都显示在一起了 1.下面,我们来设置一下,这些“待选项”按钮的坐标, 现在,“待选项”按钮的坐标,是不是都在同一个位置啊, 回忆一下,这个待选项按钮,是怎么生成的, 首先,是在…...

自组织( Self-organization),自组织临界性(Self-organized criticality)
文章目录1. 自组织概述原则历史按领域物理化学生物学2. 自组织临界性概述3. 自组织临界性的特征4. 自组织临界模型5. 自然界中的自组织临界6. 自组织临界性和优化7. 自组织临界性的控制7.1 方案7.2 应用1. 自组织 wiki: Self-organization 图 200 C 水热处理过程中微米级 Nb3O…...
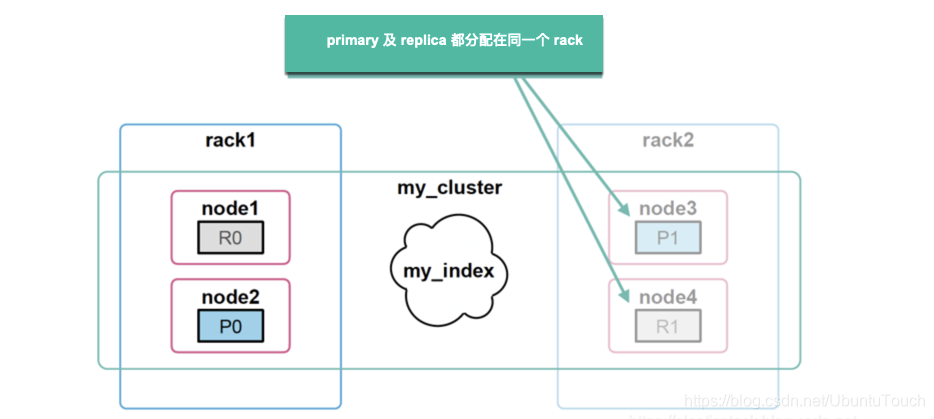
Elasticsearch:集群管理
在今天的文章中,我们应该学习如何管理我们的集群。 备份和分片分配是我们应该能够执行的基本任务。 分片分配过滤 Elasticsearch 将索引配到一个或多个分片中,我们可以将这些分片保存在特定的集群节点中。 例如,假设你有多个数据集群节点&am…...
| 机考必刷)
华为OD机试题 - 非严格递增连续数字序列(JavaScript)| 机考必刷
更多题库,搜索引擎搜 梦想橡皮擦华为OD 👑👑👑 更多华为OD题库,搜 梦想橡皮擦 华为OD 👑👑👑 更多华为机考题库,搜 梦想橡皮擦华为OD 👑👑👑 华为OD机试题 最近更新的博客使用说明本篇题解:非严格递增连续数字序列题目输入输出示例一输入输出说明Code解题…...

lc23. 合并K个升序链表
题目描述给你一个链表数组,每个链表都已经按升序排列。请你将所有链表合并到一个升序链表中,返回合并后的链表。示例 1:输入:lists [[1,4,5],[1,3,4],[2,6]]输出:[1,1,2,3,4,4,5,6]解释:链表数组如下&…...
Java笔记029-泛型
泛型泛型的理解和好处看一个需求请编写程序,在ArrayList中,添加3个Dog对象Dog对象含有name和age,并输出name和age(要求使用getXxx)先用传统的方法来解决->引出泛型package com15.generic;import java.util.ArrayList;/*** author 甲柒* ve…...

港科夜闻|香港科大与中国联通成立联合实验室,推动智慧社会研究发展
关注并星标每周阅读港科夜闻建立新视野 开启新思维1、香港科大与中国联通成立联合实验室,推动智慧社会研究发展。香港科大与中国联通于3月9日签署两份协议以加强战略合作,并成立「香港科技大学 - 中国联通智慧社会联合实验室」,就香港科大建构…...
制作一个简单的信用卡验证表
下载:https://download.csdn.net/download/mo3408/87559584 效果图: 您可以从文章顶部附近的下载按钮获取该项目的完整代码。这些文件的概述如下所示: 我们需要将两个 .css 文件和两个 .js 文件包含在我们的 HTML 中。所有其他资源,例如 Bootstrap 框架、jQuery 和 Web 字…...

牛客小白月赛68
牛客小白月赛68A Tokitsukaze and New OperationB Tokitsukaze and Order Food DeliveryC Tokitsukaze and Average of SubstringD Tokitsukaze and Development TaskE Tokitsukaze and Colorful ChessboardF Tokitsukaze and New RenKinKama题目链接A Tokitsukaze and New Ope…...

超短脉冲激光自聚焦效应
前言与目录 强激光引起自聚焦效应机理 超短脉冲激光在脆性材料内部加工时引起的自聚焦效应,这是一种非线性光学现象,主要涉及光学克尔效应和材料的非线性光学特性。 自聚焦效应可以产生局部的强光场,对材料产生非线性响应,可能…...

linux 错误码总结
1,错误码的概念与作用 在Linux系统中,错误码是系统调用或库函数在执行失败时返回的特定数值,用于指示具体的错误类型。这些错误码通过全局变量errno来存储和传递,errno由操作系统维护,保存最近一次发生的错误信息。值得注意的是,errno的值在每次系统调用或函数调用失败时…...

2021-03-15 iview一些问题
1.iview 在使用tree组件时,发现没有set类的方法,只有get,那么要改变tree值,只能遍历treeData,递归修改treeData的checked,发现无法更改,原因在于check模式下,子元素的勾选状态跟父节…...

SpringBoot+uniapp 的 Champion 俱乐部微信小程序设计与实现,论文初版实现
摘要 本论文旨在设计并实现基于 SpringBoot 和 uniapp 的 Champion 俱乐部微信小程序,以满足俱乐部线上活动推广、会员管理、社交互动等需求。通过 SpringBoot 搭建后端服务,提供稳定高效的数据处理与业务逻辑支持;利用 uniapp 实现跨平台前…...

Cloudflare 从 Nginx 到 Pingora:性能、效率与安全的全面升级
在互联网的快速发展中,高性能、高效率和高安全性的网络服务成为了各大互联网基础设施提供商的核心追求。Cloudflare 作为全球领先的互联网安全和基础设施公司,近期做出了一个重大技术决策:弃用长期使用的 Nginx,转而采用其内部开发…...

ServerTrust 并非唯一
NSURLAuthenticationMethodServerTrust 只是 authenticationMethod 的冰山一角 要理解 NSURLAuthenticationMethodServerTrust, 首先要明白它只是 authenticationMethod 的选项之一, 并非唯一 1 先厘清概念 点说明authenticationMethodURLAuthenticationChallenge.protectionS…...
详解:相对定位 绝对定位 固定定位)
css的定位(position)详解:相对定位 绝对定位 固定定位
在 CSS 中,元素的定位通过 position 属性控制,共有 5 种定位模式:static(静态定位)、relative(相对定位)、absolute(绝对定位)、fixed(固定定位)和…...

Redis数据倾斜问题解决
Redis 数据倾斜问题解析与解决方案 什么是 Redis 数据倾斜 Redis 数据倾斜指的是在 Redis 集群中,部分节点存储的数据量或访问量远高于其他节点,导致这些节点负载过高,影响整体性能。 数据倾斜的主要表现 部分节点内存使用率远高于其他节…...

AI书签管理工具开发全记录(十九):嵌入资源处理
1.前言 📝 在上一篇文章中,我们完成了书签的导入导出功能。本篇文章我们研究如何处理嵌入资源,方便后续将资源打包到一个可执行文件中。 2.embed介绍 🎯 Go 1.16 引入了革命性的 embed 包,彻底改变了静态资源管理的…...

代理篇12|深入理解 Vite中的Proxy接口代理配置
在前端开发中,常常会遇到 跨域请求接口 的情况。为了解决这个问题,Vite 和 Webpack 都提供了 proxy 代理功能,用于将本地开发请求转发到后端服务器。 什么是代理(proxy)? 代理是在开发过程中,前端项目通过开发服务器,将指定的请求“转发”到真实的后端服务器,从而绕…...
