4.1 四个子空间的正交性
一、四个子空间的正交性
如果两个向量的点积为零,则两个向量正交: v ⋅ w = v T w = 0 \boldsymbol v\cdot\boldsymbol w=\boldsymbol v^T\boldsymbol w=0 v⋅w=vTw=0。本章着眼于正交子空间、正交基和正交矩阵。两个子空间的中的向量,一组基中的向量和 Q Q Q 中的列向量,它们所有的配对向量都是正交的。对于直角三角形有 a 2 + b 2 = c 2 a^2+b^2=c^2 a2+b2=c2,两条直角边分别是 v \boldsymbol v v 和 w \boldsymbol w w。
正交向量 v T w = 0 且 ∣ ∣ v ∣ ∣ 2 + ∣ ∣ w ∣ ∣ 2 = ∣ ∣ v − w ∣ ∣ 2 \pmb{正交向量}\kern 35pt\boldsymbol v^T\boldsymbol w=0\,且\,||\boldsymbol v||^2+||\boldsymbol w||^2=||\boldsymbol v-\boldsymbol w||^2 正交向量vTw=0且∣∣v∣∣2+∣∣w∣∣2=∣∣v−w∣∣2
当 v T w = w T v = 0 \boldsymbol v^T\boldsymbol w=\boldsymbol w^T\boldsymbol v=0 vTw=wTv=0 时,右边 ( v + w ) T ( v − w ) = v T v + w T w (\boldsymbol v+\boldsymbol w)^T(\boldsymbol v-\boldsymbol w)=\boldsymbol v^T\boldsymbol v+\boldsymbol w^T\boldsymbol w (v+w)T(v−w)=vTv+wTw。
第三章我们主要是讨论 A x = b A\boldsymbol x=\boldsymbol b Ax=b,我们需要列空间和零空间,然后视线转到 A T A^T AT,会需要另外两个子空间。这四个基本子空间揭示了矩阵实际上在做什么。
矩阵乘向量: A A A 乘 x \boldsymbol x x:第一层只有数字;第二层 A x A\boldsymbol x Ax 表示的是列向量的组合;第三层展示了子空间。在学习 Figure4.2 的大图之后,我们将看到它的全貌。
将子空间放在一起可以显示出 A A A 乘 x \boldsymbol x x 隐藏的一些事实,两个子空间之间的 90 ° 90° 90° 角就是我们将要讨论的新的主题。
行空间垂直于零空间。 A A A 的每一行垂直于 A x = 0 A\boldsymbol x=\boldsymbol 0 Ax=0 的每一个解。得到 Figure 4.2 左侧的 90 ° 90° 90° 角。子空间的垂直性是线性代数基本定理的第二部分。
列空间垂直于 A T A^T AT 的零空间。当 b \boldsymbol b b 不在列空间中,此时将无法求解 A x = b A\boldsymbol x=\boldsymbol b Ax=b,那么 A T A^T AT 的零空间将展现出它的优势。它包含有 “最小二乘” 解法的误差 e = b − A x \boldsymbol e=\boldsymbol b-A\boldsymbol x e=b−Ax。最小二乘法是线性代数在本章的关键应用。
线性代数基本定理的第一部分给出了子空间的维度。行空间与列空间有相同的维度 r r r,剩下两个零空间的维度分别是 n − r n-r n−r 和 m − r m-r m−r。现在我们将证明行空间与零空间是 R n R^n Rn 中的正交子空间。
定义 \kern 10pt 如果向量空间中的两个子空间 V \boldsymbol V V 和 W \boldsymbol W W 有:任意 V \boldsymbol V V 中的向量 v \boldsymbol v v 和任意 W \boldsymbol W W 中的向量 w \boldsymbol w w 都垂直,则 V \boldsymbol V V 和 W \boldsymbol W W 正交:
正交子空间 对于所有 V 中的向量 v 和所有 W 中的向量 w 都有 v T w = 0 \pmb{正交子空间}\kern 30pt对于所有\,\boldsymbol V\,中的向量 \,\boldsymbol v\,和所有\,\boldsymbol W\,中的向量\,\boldsymbol w\,都有\,\boldsymbol v^T\boldsymbol w=0 正交子空间对于所有V中的向量v和所有W中的向量w都有vTw=0
【例1】房间中的地板(延伸到无限远)是一个子空间 V \boldsymbol V V,两面墙的交线是一个子空间 W \boldsymbol W W(一维)。这两个子空间是正交的。两面墙交线上的每个向量与地板上的每个向量都垂直。
【例2】两面墙看起来垂直,但是这两个子空间不是正交的!它们的交线同时位于 V \boldsymbol V V 和 W \boldsymbol W W,这条交线与它自身并不垂直。两个平面( R 3 \pmb{\textrm R}^3 R3 中的两个 2 2 2 维平面)不可能是正交的子空间。
当一个向量同时存在于两个正交的子空间中,那么它一定是零向量,它垂直于它本身,即是 v \boldsymbol v v 也是 w \boldsymbol w w,所以有 v T v = 0 \boldsymbol v^T\boldsymbol v=0 vTv=0,它只能是零向量。

线性代数的重要例子来源于四个基本子空间。零是零空间与行空间的唯一交点,此外, A A A 的零空间与行空间是 90 ° 90° 90° 相交。我们可以直接从 A x = 0 A\boldsymbol x=\boldsymbol 0 Ax=0 得到这个关键事实:
因为 A x = 0 A\boldsymbol x=\boldsymbol 0 Ax=0,所以有 A A A 零空间中的每个向量 x \boldsymbol x x 垂直于 A A A 的每一行。零空间 N ( A ) \pmb N(A) N(A) 和行空间 C ( A T ) \pmb C(A^T) C(AT) 是 R n \pmb {\textrm R}^n Rn 中的正交子空间。
为什么 x \boldsymbol x x 与这些行垂直呢,看 A x = 0 A\boldsymbol x=\boldsymbol 0 Ax=0,每行乘 x \boldsymbol x x:
A x = [ row 1 ⋮ row m ] [ x ] = [ 0 ⋮ 0 ] ← ( row 1 ) ⋅ x 是零 ← ( row m ) ⋅ x 是零 ( 4.1.1 ) A\boldsymbol x=\begin{bmatrix}\pmb{\textrm{row\,\,1}}\\\vdots\\{\pmb{\textrm{row}\,\,m}}\end{bmatrix}\begin{bmatrix}\,\\\boldsymbol x\\\,\end{bmatrix}=\begin{bmatrix}0\\\vdots\\0\end{bmatrix}\kern 10pt\begin{matrix}\leftarrow&(\pmb{\textrm{row\,\,1}})\cdot\boldsymbol x\,是零\\\,\\\leftarrow&(\pmb{\textrm{row}\,\,m})\cdot\boldsymbol x\,是零\end{matrix}\kern 25pt(4.1.1) Ax= row1⋮rowm x = 0⋮0 ←←(row1)⋅x是零(rowm)⋅x是零(4.1.1)
第一个方程表明行 1 1 1 垂直于 x \boldsymbol x x,最后一个方程表明行 m m m 垂直于 x \boldsymbol x x。每一行与 x \boldsymbol x x 的点积都是零,则 x \boldsymbol x x 也垂直于行的每种组合。整个行空间 C ( A T ) \pmb C(A^T) C(AT) 与零空间 N ( A ) \pmb N(A) N(A) 正交。
第二种证明正交的方式使用矩阵的缩写:行空间的向量就是行的线性组合 A T y A^T\boldsymbol y ATy,做 A T y A^T\boldsymbol y ATy 与零空间任意向量 x \boldsymbol x x 的点积,可以得到这些向量是垂直的: 零空间与行空间正交 x T ( A T y ) = ( A x ) T y = 0 T y = 0 ( 4.1.2 ) \pmb{零空间与行空间正交}\kern 15pt\boldsymbol x^T(A^T\boldsymbol y)=(A\boldsymbol x)^T\boldsymbol y=\boldsymbol 0^T\boldsymbol y=0\kern 20pt(4.1.2) 零空间与行空间正交xT(ATy)=(Ax)Ty=0Ty=0(4.1.2)第一个证明很直观,从方程(4.1.1)中可以直接看到 A A A 的这些行乘 x \boldsymbol x x 得到零。第二个证明表示了为什么 A A A 和 A T A^T AT 都在基础定理中。
【例3】 A A A 的行垂直于零空间中的向量 x = ( 1 , 1 , − 1 ) \boldsymbol x=(1,1,-1) x=(1,1,−1): A x = [ 1 3 4 5 2 7 ] [ 1 1 − 1 ] = [ 0 0 ] 得点积 1 + 3 − 4 = 0 5 + 2 − 7 = 0 A\boldsymbol x=\begin{bmatrix}1&3&4\\5&2&7\end{bmatrix}\begin{bmatrix}\kern 7pt1\\\kern 7pt1\\-1\end{bmatrix}=\begin{bmatrix}0\\0\end{bmatrix}\kern 10pt得点积\kern 5pt\begin{matrix}1+3-4=0\\5+2-7=0\end{matrix} Ax=[153247] 11−1 =[00]得点积1+3−4=05+2−7=0现在我们将实现转向另外两个子空间。此例中,列空间是整个 R 2 \boldsymbol {\textrm R}^2 R2, A T A^T AT 的零空间只有零向量(与任意向量正交)。 A A A 的列空间和 A T A^T AT 的零空间总是正交的子空间。
A T A^T AT 零空间中的每个向量 y \boldsymbol y y 垂直于 A A A 的每一列。左零空间 N ( A T ) \pmb N(A^T) N(AT) 和列空间 C ( A ) \pmb C(A) C(A) 是 R m \textrm{\textrm R}^m Rm 中的正交子空间。
因为 A T A^T AT 的零空间与 A T A^T AT 的行空间正交,而 A T A^T AT 的零空间就是 A A A 的左零空间, A T A^T AT 的行空间就是 A A A 的列空间。证毕!
看 A T y = 0 A^T\boldsymbol y=\boldsymbol 0 ATy=0 可以得到一个可视化的证明。 A A A 的每一列乘 y \boldsymbol y y 都得到 0 0 0: C ( A ) ⊥ N ( A T ) A T y = [ ( column 1 ) T ⋯ ( column n ) T ] [ y ] = [ 0 ˙ 0 ] ( 4.2.3 ) \pmb C(A)\perp \pmb N(A^T)\kern 15ptA^T\boldsymbol y=\begin{bmatrix}(\pmb{\textrm{column}\,\,1})^T\\\cdots\\(\pmb{\textrm{column}\,\,n})^T\end{bmatrix}\begin{bmatrix}\\\boldsymbol y\\\,\end{bmatrix}=\begin{bmatrix}0\\\dot\ \\0\end{bmatrix}\kern 25pt(4.2.3) C(A)⊥N(AT)ATy= (column1)T⋯(columnn)T y = 0 ˙0 (4.2.3) y \boldsymbol y y 和 A A A 的每一列点积都是零,则有 A A A 左零空间中的向量 y \boldsymbol y y 垂直于 A A A 的每一列,即垂直于列空间。

二、正交补
重要: 基本子空间不仅仅是正交(成对)而已,它们也要有合适的维度。两条直线可能在 R 3 \textrm{\pmb R}^3 R3 空间中垂直,但是这些直线不可能是 3 × 3 3\times3 3×3 矩阵的行空间和零空间。这两天直线的维度都是 1 1 1,相加起来是 2 2 2,但是正确的维度 r r r 与 n − r n-r n−r 加起来一定是 n = 3 n=3 n=3。
3 × 3 3\times3 3×3 矩阵的基本子空间的维度可能是 2 2 2 和 1 1 1,或 3 3 3 和 0 0 0,这些成对的子空间不仅仅是正交,它们是正交补。
定义: 子空间 V \pmb V V 的正交补包含所有与 V \pmb V V 垂直的向量。这个子空间的正交补写成 V ⊥ \pmb V^{\perp} V⊥(读作 “ V \pmb V V perp”)。
根据这个定义,零空间是行空间的正交补,每个垂直于所有行的向量 x \boldsymbol x x 都满足 A x = 0 A\boldsymbol x=\boldsymbol 0 Ax=0,它也在零空间中。
反过来也是正确的,如果 v \boldsymbol v v 与零空间正交,它一定在行空间中。否则我们可以将 v \boldsymbol v v 加入矩阵当做额外的一行,这样没有改变它的零空间,但是行空间会变大,将违反 r + ( n − r ) = n r+(n-r)=n r+(n−r)=n 的法则。结论是零空间的正交补 N ( A ) ⊥ \pmb N(A)^{\perp} N(A)⊥ 就是行空间 C ( A T ) \pmb C(A^T) C(AT)。
同样的方法,左零空间和列空间是 R m \pmb{\textrm R}^m Rm 的正交补。它们的维度 r r r 和 m − r m-r m−r 加起来得到全维度 m m m。
线性代数基本定理,第二部分 N ( A ) 是行空间 C ( A T ) 的正交补 ( 在 R n 中 ) N ( A T ) 是列空间 C ( A ) 的正交补 ( 在 R m 中 ) \pmb{线性代数基本定理,第二部分}\\{\pmb N(A)\,\pmb{是行空间}\,\pmb C(A^T)\,\pmb{的正交补(在}\,\textrm{\pmb{R}}^n\,\pmb{中)}}\\\pmb N(A^T)\,\pmb{是列空间}\,\pmb C(A)\,\pmb{的正交补(在}\,\textrm{\pmb R}^m\,\pmb{中)} 线性代数基本定理,第二部分N(A)是行空间C(AT)的正交补(在Rn中)N(AT)是列空间C(A)的正交补(在Rm中)
第一部分给出了子空间的维度,第二部分给出了它们之间的 90 ° 90° 90° 角。补充的重点是每一个 x \boldsymbol x x 都可以分成一个行空间分量 x r \boldsymbol x_r xr 和一个零空间分量 x n \boldsymbol x_n xn。Figure 4.3 显示了当 A A A 乘 x = x r + x n \boldsymbol x=\boldsymbol x_r+\boldsymbol x_n x=xr+xn 时发生了什么 A x = A x r + A x n A\boldsymbol x=A\boldsymbol x_r+A\boldsymbol x_n Ax=Axr+Axn: 零空间的分量得到零: A x n = 0 行空间的分量到列空间: A x r = A x 零空间的分量得到零:A\boldsymbol x_n=\boldsymbol 0\\行空间的分量到列空间:A\boldsymbol x_r=A\boldsymbol x 零空间的分量得到零:Axn=0行空间的分量到列空间:Axr=Ax每个向量都到列空间!左乘 A A A 不会做其它的事情,除此之外,列空间的每个向量 b \boldsymbol b b 仅来自一个行空间的唯一向量 x r \boldsymbol x_r xr。证明:如果 A x r = A x r ′ A\boldsymbol x_r=A\boldsymbol x_r' Axr=Axr′,它们的差 x r − x r ′ \boldsymbol x_r-\boldsymbol x_r' xr−xr′ 在零空间中,也会在行空间中,因为 x r \boldsymbol x_r xr 和 x r ′ \boldsymbol x_r' xr′ 都来自与行空间。它们的差必定为零,因为零空间与行空间是垂直的,因此 x r = x r ′ \boldsymbol x_r=\boldsymbol x_r' xr=xr′。
如果我们抛开两个零空间,则 A A A 中会隐藏有一个 r × r r\times r r×r 的可逆矩阵,从行空间到列空间, A A A 是可逆的。
【例4】每个秩 r r r 的矩阵都有一个 r × r r\times r r×r 的可逆子矩阵: A = [ 3 0 0 0 0 0 5 0 0 0 0 0 0 0 0 ] 包含子矩阵 [ 3 0 0 5 ] A=\begin{bmatrix}3&0&0&0&0\\0&5&0&0&0\\0&0&0&0&0\end{bmatrix}\kern 5pt包含子矩阵\kern 5pt\begin{bmatrix}3&0\\0&5\end{bmatrix} A= 300050000000000 包含子矩阵[3005]另外 11 11 11 个 0 0 0 是负责零空间的。 B B B 的秩也为 r = 2 r=2 r=2。 B = [ 1 2 3 4 5 1 2 4 5 6 1 2 4 5 6 ] 包含子矩阵 [ 1 3 1 4 ] 在主元行和主元列 B=\begin{bmatrix}1&2&3&4&5\\1&2&4&5&6\\1&2&4&5&6\end{bmatrix}\kern 5pt包含子矩阵\kern 5pt\begin{bmatrix}1&3\\1&4\end{bmatrix}在主元行和主元列 B= 111222344455566 包含子矩阵[1134]在主元行和主元列当我们选择了正确的 R n \pmb {\textrm R}^n Rn 和 R m \textrm {\pmb R}^m Rm 的基,每个矩阵都可以对角化。这个奇异值分解(Singular Value Decomposition)在应用中已经非常重要。
我们重复下一个事实, A A A 的行不可能在 A A A 的零空间中(除了零向量)。唯一都存在于两个正交子空间的向量是零向量。 如果向量 v 正交于它本身,则 v 是零向量。 \pmb{如果向量\,\boldsymbol v\,正交于它本身,则\,\boldsymbol v\,是零向量。} 如果向量v正交于它本身,则v是零向量。
三、画出大图
大图要显示出这些子空间的正交性。Figure4.4是一条直线与一个平面的正交图,它们是在三维空间中。

四、从子空间中组合基
基是线性无关的向量,它们可以张成向量空间。正常情况下对于基来说我们要检验以下两个性质,当其中一个成立时是可以退出另外一个的:
R n \pmb{\textrm R}^n Rn 中任意 n n n 个无关向量一定可以张成空间 R n \textrm{\pmb R}^n Rn,因此它们是一组基。
任何可以张成空间 R n \textrm{\pmb R}^n Rn 的 n n n 个向量一定是无关的,所以它们是一组基。
如果向量的数量是正确的,那么基的一个性质可以推出另外一个性质,这对于任何向量空间都是成立的,我们更多关注的是 R n \pmb {\textrm R}^n Rn。当这些向量是 n × n n\times n n×n 方阵 A A A 的列时,我们可得到下面两个事实:
如果 A A A 的 n n n 列是无关的,它们张成 R n \pmb{\textrm R}^n Rn,所以 A x = b A\boldsymbol x=\boldsymbol b Ax=b 有解。
如果这 n n n 个列张成 R n \pmb{\textrm R}^n Rn,则它们是无关的, A x = b A\boldsymbol x=\boldsymbol b Ax=b 有唯一解。
唯一性推论到存在性且存在性推论到唯一性, A A A 是可逆的。如果没有自由变量,则解 x \boldsymbol x x 是唯一的,那么一定有 n n n 个主元列,通过回代可以求解 A x = b A\boldsymbol x=\boldsymbol b Ax=b(解存在)。
从反方向开始,假设 A x = b A\boldsymbol x=\boldsymbol b Ax=b 对于任意的 b \boldsymbol b b 都有解(存在解),那么消元后没有零行,有 n n n 个主元没有自由变量。零空间仅包含 x = 0 \boldsymbol x=\boldsymbol 0 x=0(唯一性)。
对于行空间和零空间的基来说,有 r + ( n − r ) = n r+(n-r)=n r+(n−r)=n 个向量,这 n n n 个向量是无关的,它们张成 R n \pmb{\textrm R}^n Rn。
每个 x 都是行空间 x r 和零空间 x n 的和 x r + x n 。 每个\,\boldsymbol x\,都是行空间\,\boldsymbol x_r和零空间\,\boldsymbol x_n的和\,\boldsymbol x_r+\boldsymbol x_n。 每个x都是行空间xr和零空间xn的和xr+xn。
Figure 4.3 画出了正交补的关键点 —— 它们的维度相加是 n n n,所有的向量都可以通过正交补来解释。
【例5】 A = [ 1 2 3 6 ] A=\begin{bmatrix}1&2\\3&6\end{bmatrix} A=[1326] 将 x = [ 4 3 ] \boldsymbol x=\begin{bmatrix}4\\3\end{bmatrix} x=[43] 分成 x r + x n = [ 2 4 ] + [ 2 − 1 ] \boldsymbol x_r+\boldsymbol x_n=\begin{bmatrix}2\\4\end{bmatrix}+\begin{bmatrix}\kern 7pt2\\-1\end{bmatrix} xr+xn=[24]+[2−1]。
向量 [ 2 4 ] \begin{bmatrix}2\\4\end{bmatrix} [24] 在行空间,它的正交向量 [ 2 − 1 ] \begin{bmatrix}\kern 7pt2\\-1\end{bmatrix} [2−1] 在零空间中。
五、主要内容总结
- 如果 V \boldsymbol V V 中的每个向量 v \boldsymbol v v 和 W \boldsymbol W W 中的每个向量 w \boldsymbol w w 都正交,则子空间 V \boldsymbol V V 和 W \boldsymbol W W 正交。
- 如果 W \boldsymbol W W 中包含全部垂直于 V \boldsymbol V V 的向量(反之亦然),则 V \boldsymbol V V 和 W \boldsymbol W W 是正交补。在 R n \textrm {\pmb R}^n Rn 中, V \boldsymbol V V 和 W \boldsymbol W W 的维度相加是 n n n 。
- 零空间 N ( A ) \pmb N(A) N(A) 和行空间 C ( A T ) \pmb C(A^T) C(AT) 是正交补,维度是 ( n − r ) + r = n (n-r)+r=n (n−r)+r=n,相似的,左零空间 N ( A T ) \pmb N(A^T) N(AT) 和列空间 C ( A ) \pmb C(A) C(A) 是正交补,它们的维度是 ( m − r ) + r = m (m-r)+r=m (m−r)+r=m 。
- R n \textrm{\pmb R}^n Rn 中任意 n n n 个无关的向量可以张成 R n \pmb{\textrm R}^n Rn;任意可以张成 R n \pmb{\textrm R}^n Rn 的 n n n 个向量是无关的。
六、例题
【例6】假设 S \pmb S S 是 9 维空间 R 9 \textrm{\pmb R}^9 R9 中的 6 6 6 维子空间:
(a)与 S \pmb S S 正交的子空间的维度可能是多少?
(b) S \pmb S S 的正交补 S ⊥ \pmb S^{\perp} S⊥ 的维度可能是多少?
(c)行空间是 S \pmb S S 的矩阵 A A A 可能的最小形状大小是多少?
(d)零空间是 S ⊥ \pmb S^{\perp} S⊥ 的矩阵 B B B,它的形状可能的最小大小是多少?
解: (a)如果 S \pmb S S 是 R 9 \textrm{\pmb R}^9 R9 中的 6 6 6 维子空间,那么与 S \pmb S S 正交的子空间的维度可能是 0 , 1 , 2 , 3 0,1,2,3 0,1,2,3。
(b)正交补 S ⊥ \pmb S^{\perp} S⊥ 是最大的正交子空间,它的维度是 3 3 3。
(c)最小的矩阵 A A A 形状是 6 × 9 6\times 9 6×9。(它的 6 6 6 行是 S \pmb S S 的一组基)。
(d)最小的矩阵 B B B 形状是 6 × 9 6\times9 6×9。(与(c)答案一样)
如果 B B B 的新行第 7 7 7 行是 A A A 的 6 6 6 行的组合,那么 B B B 与 A A A 有相同的行空间,也有相同的零空间。 A x = 0 A\boldsymbol x=\boldsymbol 0 Ax=0 的特殊解 s 1 , s 2 , s 3 \boldsymbol s_1,\boldsymbol s_2,\boldsymbol s_3 s1,s2,s3 同样也是 B x = 0 B\boldsymbol x=\boldsymbol 0 Bx=0 的特殊解。消元后 B B B 的第 7 7 7 行将会变成零行。
【例7】方程 x − 3 y − 4 z = 0 x-3y-4z=0 x−3y−4z=0 描述了 R 3 \textrm {\pmb R}^3 R3 中的一个平面 P \pmb P P(实际上是一个子空间)。
(a)平面 P \pmb P P 是哪个 1 × 3 1\times3 1×3 的矩阵 A A A 的零空间?
(b)找到 x − 3 y − 4 z = 0 x-3y-4z=0 x−3y−4z=0 特殊解构成的一组基 s 1 , s 2 \boldsymbol s_1,\boldsymbol s_2 s1,s2(它们会是零空间矩阵 N N N 的列)。
(c)找到垂直于 P \pmb P P 的直线 P ⊥ \pmb P^{\perp} P⊥ 的一组基。
解:(a) A = [ 1 − 3 − 4 ] A=\begin{bmatrix}1&-3&-4\end{bmatrix} A=[1−3−4]
(b) s 1 = [ 3 1 0 ] , s 2 = [ 4 0 1 ] \boldsymbol s_1=\begin{bmatrix}3\\1\\0\end{bmatrix},\kern 5pt\boldsymbol s_2=\begin{bmatrix}4\\0\\1\end{bmatrix} s1= 310 ,s2= 401
(c) [ 1 − 3 − 4 ] \begin{bmatrix}\kern 7pt1\\-3\\-4\end{bmatrix} 1−3−4
相关文章:

4.1 四个子空间的正交性
一、四个子空间的正交性 如果两个向量的点积为零,则两个向量正交: v ⋅ w v T w 0 \boldsymbol v\cdot\boldsymbol w\boldsymbol v^T\boldsymbol w0 v⋅wvTw0。本章着眼于正交子空间、正交基和正交矩阵。两个子空间的中的向量,一组基中的向…...
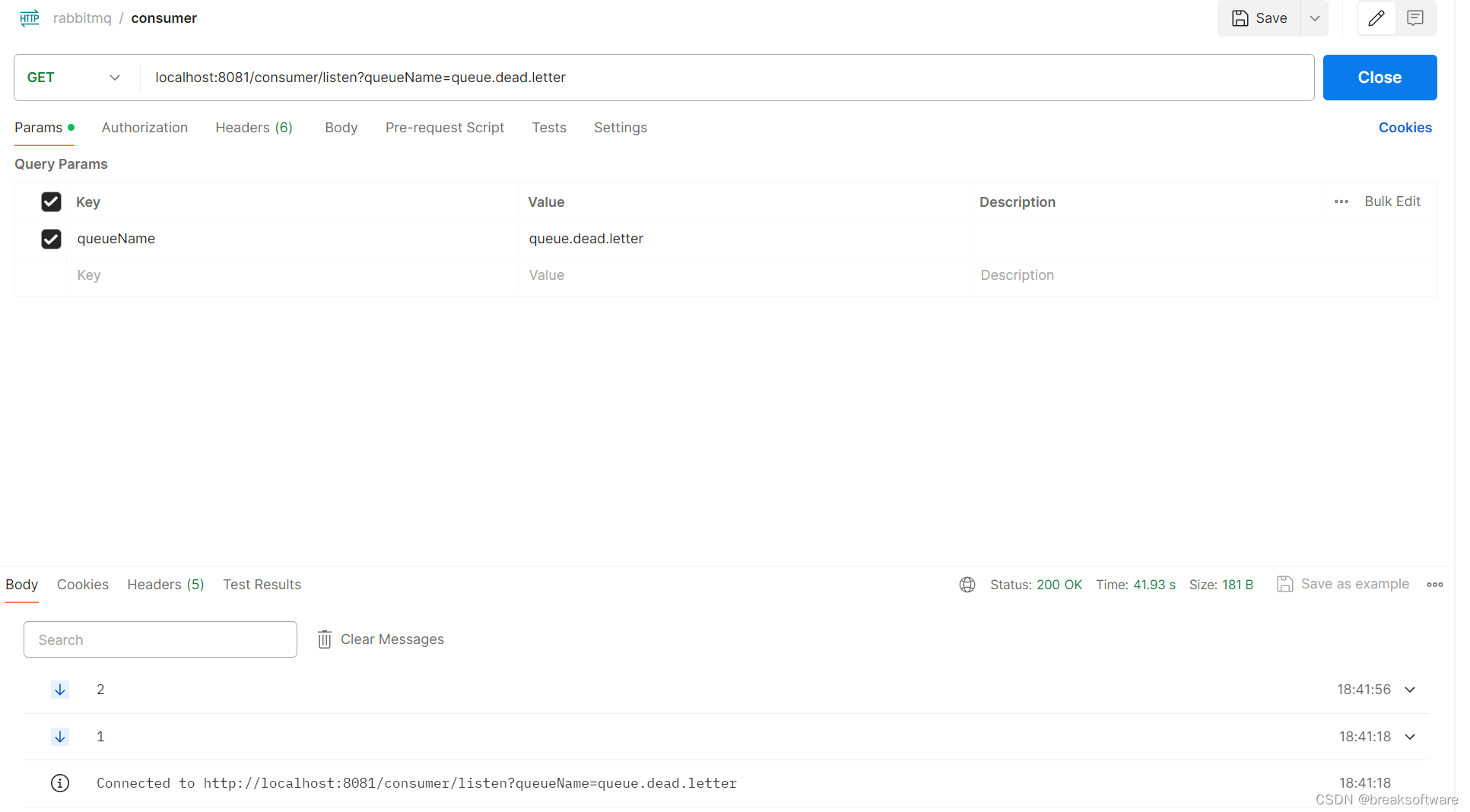
RabbitMQ实践——使用WebFlux响应式方式实时返回队列中消息
大纲 Pom.xml监听队列实时返回消息测试完整代码工程代码 在之前的案例中,我们在管理后台收发消息都是通过短连接的形式。本文我们将探索对队列中消息的实时读取,并通过流式数据返回给客户端。 webflux是反应式Web框架,客户端可以通过一个长连…...

SpringBoot前后端传递数据时常用的JSON格式数据是什么?【讲解JSON概念、语法、以及Java对象互转】
SpringBoot前后端传递数据时常用的JSON格式数据是什么? JSON概念JSON语法JSON的两种结构:JSON字符串和Java对象互转:objectMapper.writeValueAsString(person);objectMapper.readValue(jsonStr,Person.class); 在SpringMVC框架中,…...

mysql学习——SQL中的DQL和DCL
SQL中的DQL和DCL DQL基本查询条件查询聚合函数分组查询排序查询分页查询 DCL管理用户权限控制 学习黑马MySQL课程,记录笔记,用于复习。 DQL DQL英文全称是Data Query Language(数据查询语言),数据查询语言,用来查询数据库中表的记…...
windows系统上nginx搭建文件共享
1、下载windows版nginx 下载地址 2、配置nginx 编辑nginx.conf配置文件 在http模块下添加这个参数 underscores_in_headers on;#修改location内容,共享哪个文件夹,就写哪个文件夹,最后一定要跟上/,否则无法访问 location / {…...
星闪指向遥控,做家电交互的破壁人
“面壁者罗辑,我是你的破壁人。” 科幻小说《三体》中,当人类的基础科学被三体人封锁,变得停步不前,人类启动了自救的面壁计划,通过一次又一次破壁,找到战胜三体人的办法。 现实中,有一点已经成…...
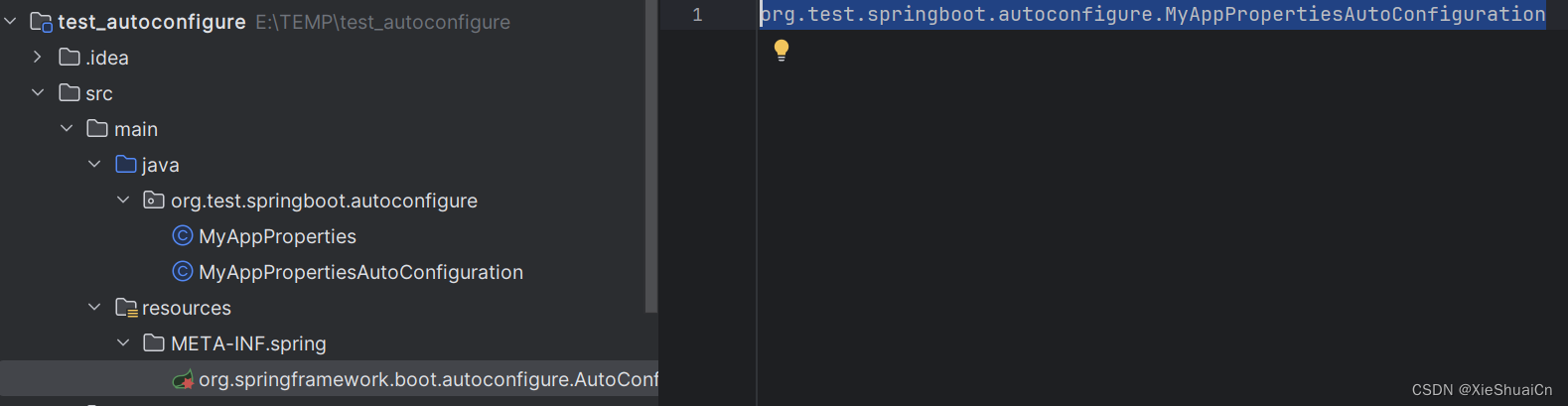
SpringBoot使用AutoConfigure实现依赖库自动导入配置
我们知道导入配置有两种,一种是Value,一种是ConfigurationProperties,将对应的类标记为Component即可导入。但是被注解标识的类创建Bean有一个前提,只对启动类所在的包路径下的所有带有Component等注解的类才会创建Bean。如果我们…...
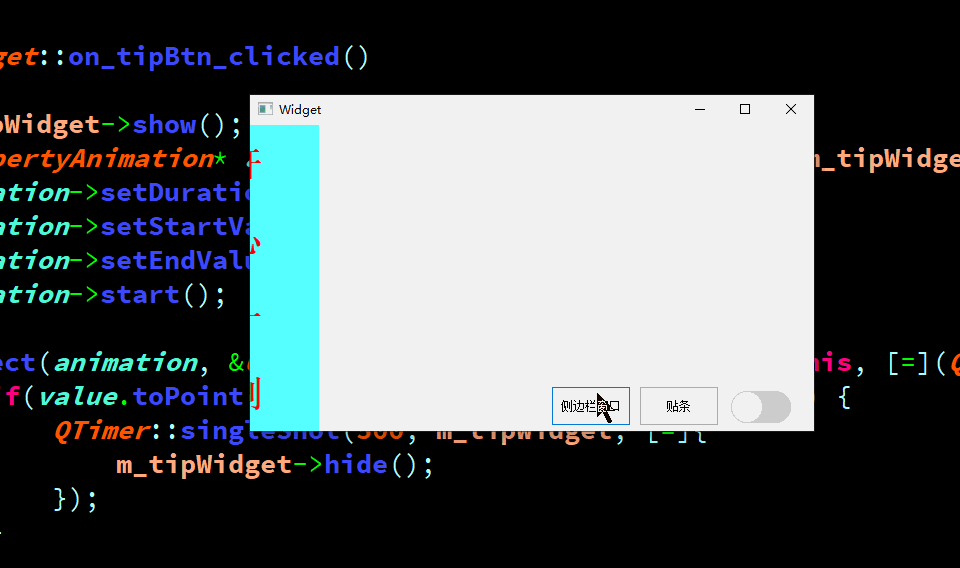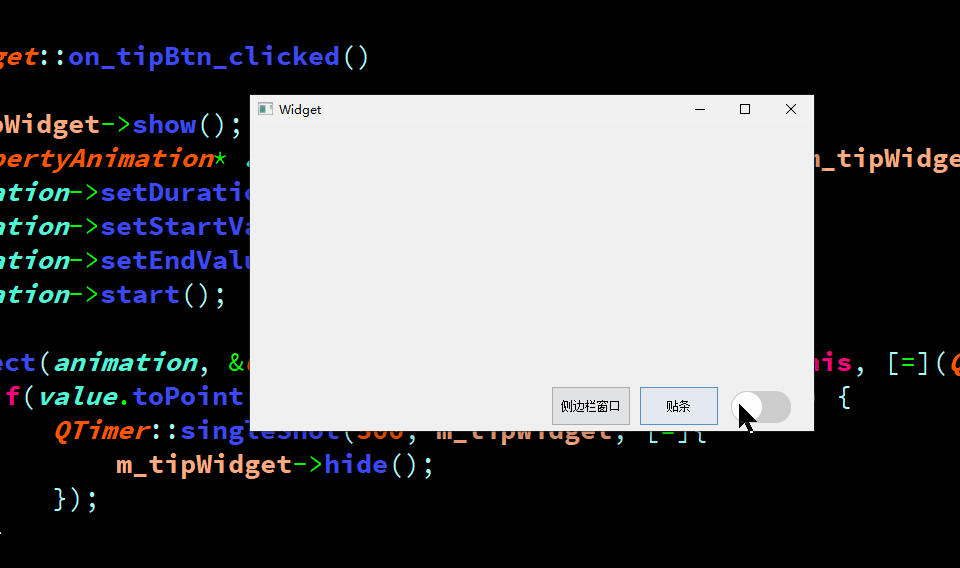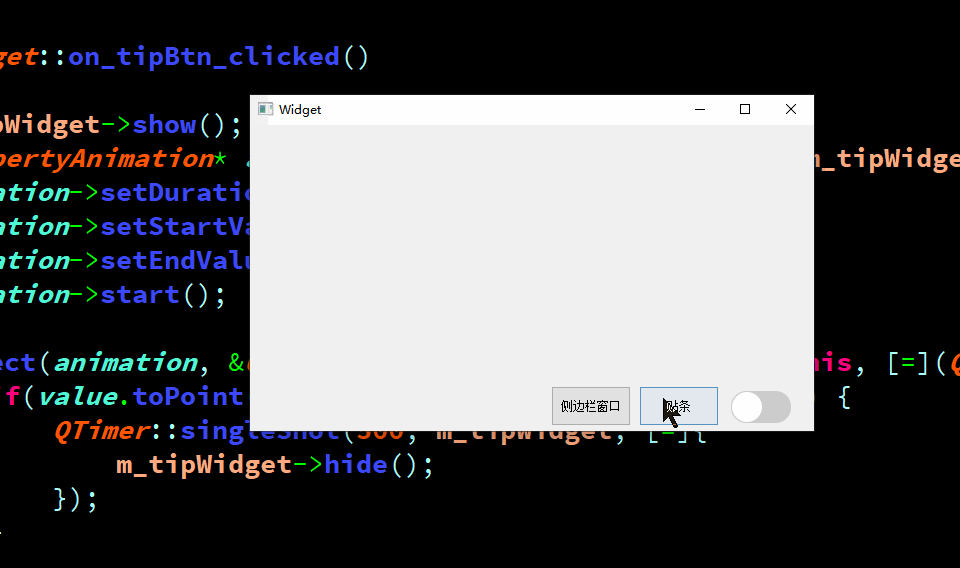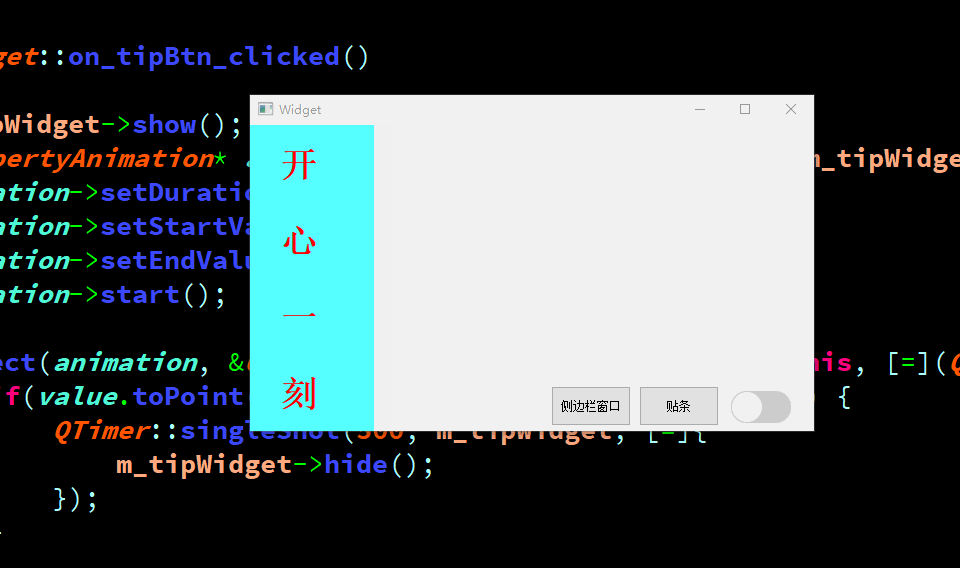
QT中利用动画弄一个侧边栏窗口,以及贴条效果
1、效果 2、关键代码 void Widget::on_sliderBtn_clicked() {m_sliderWidget->show();QPropertyAnimation* animation = new QPropertyAnimation(m...

win10免安装配置MySQL8.4.0
注:此教程基于win10 22H2 版本 1、下载最新版本MySQL压缩包 下载链接:MySQL官网下载地址 点击第二行的 ZIP Archive 后面的Download(当前时间2024-06-19最新版本是8.4.0) 2、解压并添加配置文件 下载完毕后,解压缩…...
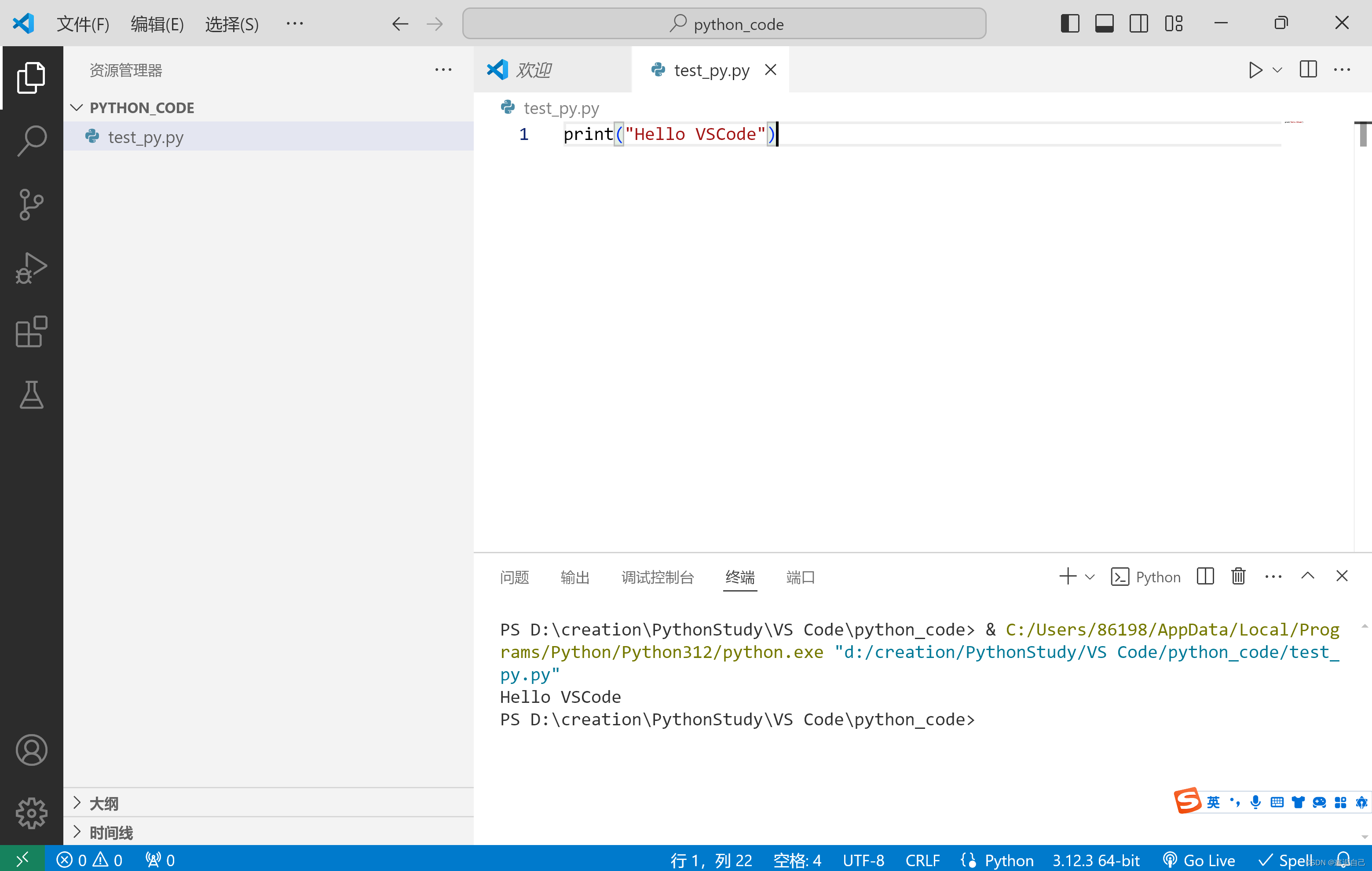
VS Code安装及环境配置(超详细)
VS Code简介 Visual Studio Code(简称 VS Code )是 Microsoft 于2015年4月发布的一款代码编辑器,以界面简洁、轻量著称。 它是一款免费开源的现代化轻量级代码编辑器,支持几乎所有主流开发语言的语法高亮、智能代码补全、自定义…...

shell脚本通过解析日志使用串口开关屏知识点整理
#!/bin/bash #logPath 写日志的存放路径 #logPath/home/workspace/tvs/trainborne logPath/home/firefly tmpFile$$ function getLogName() { #echo "$logPath/LCDController_"date "%Y%m%d000000.log" echo "LCDController_20240424000000.log&quo…...

速盾:视频cdn和网站cdn的相同点与不同点
CDN(Content Delivery Network)是一种分布式网络架构,旨在为用户提供高效、高质量的内容传送服务。CDN主要通过将内容分发到全球各地的边缘节点,并根据用户的地理位置选择最近的节点来提供内容,从而加速内容的传输并降…...

37.自定义协议
自定义协议要素 1.魔数:用来第一时间判定是否是无效数据包。 2.版本号:主持协议升级。 3.序列化算法:消息正文到底采用那种序列化方式,可以由此扩展,例如:json,protobuf(google的序列化算法,基于二进制,虽然可读性不好,但是字节数占用更少),hessian(基于二进制)…...
【React Native】measureInWindow在安卓上无法正确获取View在屏幕上的布局信息
问题描述: 在React Native中,我们可以使用measureInWindow的方式去获取一个View在屏幕中的位置信息: 下面这个Demo中,我们写了一个页面HomePage和一个列表项组件ListItemA,我们期望每过5s监测一次列表中每一项在屏幕中…...

C++ 教程 - 04 类的使用
文章目录 类的定义类定义案例构造函数 类的定义 C 在 C 语言的基础上增加面向对象编程,类是用于指定对象的形式,是一种用户自定义的数据类型,封装了数据和函数。类可以被看作是一种模板,可以用来创建具有相同属性和行为的多个对象…...

excel按模板文件导出多个文件并压缩为ZIP格式返回前端
思路:先准备好模板文件和与之对应的实体类,数据库数据等,还是之前思路,根据查出的数据,填充模板文件,生成一个临时文件,最后将这些个临时文件打包为zip返回前端,并将多个临时文件删除…...

自动驾驶仿真测试用例表格示例 ACC ELK FCW
自动驾驶仿真测试用例表格示例 测试用例概览 本测试用例表格涵盖了自动驾驶系统中多个关键功能和场景的测试,旨在确保系统在不同条件下的表现和稳定性。 用例编号测试项目测试描述预期结果实际结果通过/失败TC-001ACC功能测试在高速公路上启用ACC,测试车…...

数组 (java)
文章目录 一维数组静态初始化动态初始化 二维数组静态初始化动态初始化 数组参数传递可变参数关于 main 方法的形参 argsArray 工具类sort 中的 comparable 和 comparatorcomparator 比较器排序comparable 自然排序 一维数组 线性结构 静态初始化 第一种:int[] a…...
时序预测 | Matlab基于Transformer多变量时间序列多步预测
目录 效果一览基本介绍程序设计参考资料 效果一览 基本介绍 1.Matlab基于Transformer多变量时间序列多步预测; 2.多变量时间序列数据集(负荷数据集),采用前96个时刻预测的特征和负荷数据预测未来96个时刻的负荷数据; 3…...

suuk-s.php.jpg-python 库劫持
做virtualBox的端口映射吧 suukmedim文件白名单绕过、反弹shell、$paht环境变量更改、python 库劫持提权、Reptile提权、sandfly-processdecloak使用 服务扫描 ┌──(kali㉿kali)-[~] └─$ sudo nmap -sV -A -T 4 -p 22,80 192.168.18.238GetSHell 访问80http://192.168.…...

Docker 离线安装指南
参考文章 1、确认操作系统类型及内核版本 Docker依赖于Linux内核的一些特性,不同版本的Docker对内核版本有不同要求。例如,Docker 17.06及之后的版本通常需要Linux内核3.10及以上版本,Docker17.09及更高版本对应Linux内核4.9.x及更高版本。…...

业务系统对接大模型的基础方案:架构设计与关键步骤
业务系统对接大模型:架构设计与关键步骤 在当今数字化转型的浪潮中,大语言模型(LLM)已成为企业提升业务效率和创新能力的关键技术之一。将大模型集成到业务系统中,不仅可以优化用户体验,还能为业务决策提供…...

【杂谈】-递归进化:人工智能的自我改进与监管挑战
递归进化:人工智能的自我改进与监管挑战 文章目录 递归进化:人工智能的自我改进与监管挑战1、自我改进型人工智能的崛起2、人工智能如何挑战人类监管?3、确保人工智能受控的策略4、人类在人工智能发展中的角色5、平衡自主性与控制力6、总结与…...
)
云计算——弹性云计算器(ECS)
弹性云服务器:ECS 概述 云计算重构了ICT系统,云计算平台厂商推出使得厂家能够主要关注应用管理而非平台管理的云平台,包含如下主要概念。 ECS(Elastic Cloud Server):即弹性云服务器,是云计算…...

在四层代理中还原真实客户端ngx_stream_realip_module
一、模块原理与价值 PROXY Protocol 回溯 第三方负载均衡(如 HAProxy、AWS NLB、阿里 SLB)发起上游连接时,将真实客户端 IP/Port 写入 PROXY Protocol v1/v2 头。Stream 层接收到头部后,ngx_stream_realip_module 从中提取原始信息…...

IoT/HCIP实验-3/LiteOS操作系统内核实验(任务、内存、信号量、CMSIS..)
文章目录 概述HelloWorld 工程C/C配置编译器主配置Makefile脚本烧录器主配置运行结果程序调用栈 任务管理实验实验结果osal 系统适配层osal_task_create 其他实验实验源码内存管理实验互斥锁实验信号量实验 CMISIS接口实验还是得JlINKCMSIS 简介LiteOS->CMSIS任务间消息交互…...

Java面试专项一-准备篇
一、企业简历筛选规则 一般企业的简历筛选流程:首先由HR先筛选一部分简历后,在将简历给到对应的项目负责人后再进行下一步的操作。 HR如何筛选简历 例如:Boss直聘(招聘方平台) 直接按照条件进行筛选 例如:…...

JVM 内存结构 详解
内存结构 运行时数据区: Java虚拟机在运行Java程序过程中管理的内存区域。 程序计数器: 线程私有,程序控制流的指示器,分支、循环、跳转、异常处理、线程恢复等基础功能都依赖这个计数器完成。 每个线程都有一个程序计数…...

人工智能(大型语言模型 LLMs)对不同学科的影响以及由此产生的新学习方式
今天是关于AI如何在教学中增强学生的学习体验,我把重要信息标红了。人文学科的价值被低估了 ⬇️ 转型与必要性 人工智能正在深刻地改变教育,这并非炒作,而是已经发生的巨大变革。教育机构和教育者不能忽视它,试图简单地禁止学生使…...

Git常用命令完全指南:从入门到精通
Git常用命令完全指南:从入门到精通 一、基础配置命令 1. 用户信息配置 # 设置全局用户名 git config --global user.name "你的名字"# 设置全局邮箱 git config --global user.email "你的邮箱example.com"# 查看所有配置 git config --list…...
