随想录二刷Day17——二叉树
文章目录
- 二叉树
- 9. 二叉树的最大深度
- 10. 二叉树的最小深度
- 11. 完全二叉树的节点个数
- 12. 平衡二叉树
二叉树
9. 二叉树的最大深度
104. 二叉树的最大深度
思路1:
递归找左右子树的最大深度,选择最深的 + 1(即加上当前层)。
class Solution {
public:int maxDepth(TreeNode* root) {if (root == NULL) return 0;return max(maxDepth(root->left), maxDepth(root->right)) + 1;}
};
思路2:
利用队列层序遍历二叉树,找到最大深度
class Solution {
public:int maxDepth(TreeNode* root) {int depth = 0;if (root == NULL) return depth;queue<TreeNode *> que;que.push(root);while (!que.empty()) {int size = que.size();depth++;while (size--) {TreeNode *cur = que.front(); que.pop();if (cur->left) que.push(cur->left);if (cur->right) que.push(cur->right);}}return depth;}
};
10. 二叉树的最小深度
111. 二叉树的最小深度
思路1: 递归法
要注意只有一个子节点的情况不能统计深度,因为它不是叶子节点。深度是指根节点到叶子节点的距离。
class Solution {
public:int minDepth(TreeNode* root) {if (root == NULL) return 0;// 下面的两个判断避免了非叶子节点的情况if (!root->left && root->right) return minDepth(root->right) + 1;if (root->left && !root->right) return minDepth(root->left) + 1;return min(minDepth(root->left), minDepth(root->right)) + 1;}
};
思路2:
利用迭代法层序遍历,遇到第一个叶子节点返回深度。
class Solution {
public:int minDepth(TreeNode* root) {if (root == NULL) return 0;queue<TreeNode *> que;int depth = 0;que.push(root);while (!que.empty()) {depth++;int size = que.size();while (size--) {TreeNode *cur = que.front(); que.pop();if (!cur->left && !cur->right) return depth;if (cur->left) que.push(cur->left);if (cur->right) que.push(cur->right);}}return depth;}
};
11. 完全二叉树的节点个数
222. 完全二叉树的节点个数
思路:
满二叉树的节点数目等于 2depth−12^{depth} - 12depth−1 ,利用该条件来避免遍历整个满二叉树,只需要遍历其最左最右两分支的深度即可(O(logn)O(logn)O(logn))。遍历二叉树的递归层数 O(logn)O(logn)O(logn) 。时间复杂度是 O(logn∗logn)O(logn*logn)O(logn∗logn)
class Solution {
public:int countNodes(TreeNode* root) {if (root == NULL) return 0;// 利用满二叉树的特性优化时间复杂度TreeNode *curL = root->left;TreeNode *curR = root->right;int depthL = 0;int depthR = 0;while (curL != NULL) {curL = curL->left;depthL++;}while (curR != NULL) {curR = curR->right;depthR++;}if (depthL == depthR) return (2 << depthL) - 1;return countNodes(root->left) + countNodes(root->right) + 1;}
};
12. 平衡二叉树
110. 平衡二叉树
思路1: 递归
后序遍历统计左右子树的高度,比较左右子树高度是否满足条件。
class Solution {
public:bool isBalanced(TreeNode* root) {if (root == NULL) return true;return getHigh(root) == -1 ? false : true;}private:int getHigh(TreeNode *root) {if (root == NULL) return 0;int leftDepth = getHigh(root->left);if (leftDepth == -1) return -1;int rightDepth = getHigh(root->right);if (rightDepth == -1) return -1;if (abs(leftDepth - rightDepth) > 1) return -1; // 如果已经找到不满足底子树,就没必要再遍历了。剪枝return max(leftDepth, rightDepth) + 1;}
};
思路2: 迭代法
用栈模拟递归实现后续遍历统计二叉树深度。
再先序遍历判断左右子树深度是否满足条件。
这里没法剪枝,复杂度并不优秀。
class Solution {
public:bool isBalanced(TreeNode* root) {if (root == NULL) return true;stack<TreeNode *> stk;stk.push(root);while (!stk.empty()) {TreeNode *cur = stk.top(); stk.pop();if (abs(getHigh(cur->left) - getHigh(cur->right)) > 1) return false;if (cur->right) stk.push(cur->right);if (cur->left) stk.push(cur->left);}return true;}private:int getHigh(TreeNode *root) {if (root == NULL) return 0;stack<TreeNode *> stk;int depth = 0, result = 0;stk.push(root);while (!stk.empty()) {TreeNode *cur = stk.top(); stk.pop();if (cur) { // 后序遍历:左右中stk.push(cur); // 中stk.push(NULL);depth++;if (cur->right) stk.push(cur->right); // 右if (cur->left) stk.push(cur->left); // 左} else {cur = stk.top(); stk.pop();depth--; // 回溯}result = result > depth ? result : depth;}return result;}
};
相关文章:

随想录二刷Day17——二叉树
文章目录二叉树9. 二叉树的最大深度10. 二叉树的最小深度11. 完全二叉树的节点个数12. 平衡二叉树二叉树 9. 二叉树的最大深度 104. 二叉树的最大深度 思路1: 递归找左右子树的最大深度,选择最深的 1(即加上当前层)。 class So…...
Weblogic管理控制台未授权远程命令执行漏洞复现(cve-2020-14882/cve-2020-14883)
目录漏洞描述影响版本漏洞复现权限绕过漏洞远程命令执行声明:本文仅供学习参考,其中涉及的一切资源均来源于网络,请勿用于任何非法行为,否则您将自行承担相应后果,本人不承担任何法律及连带责任。 漏洞描述 Weblogic…...
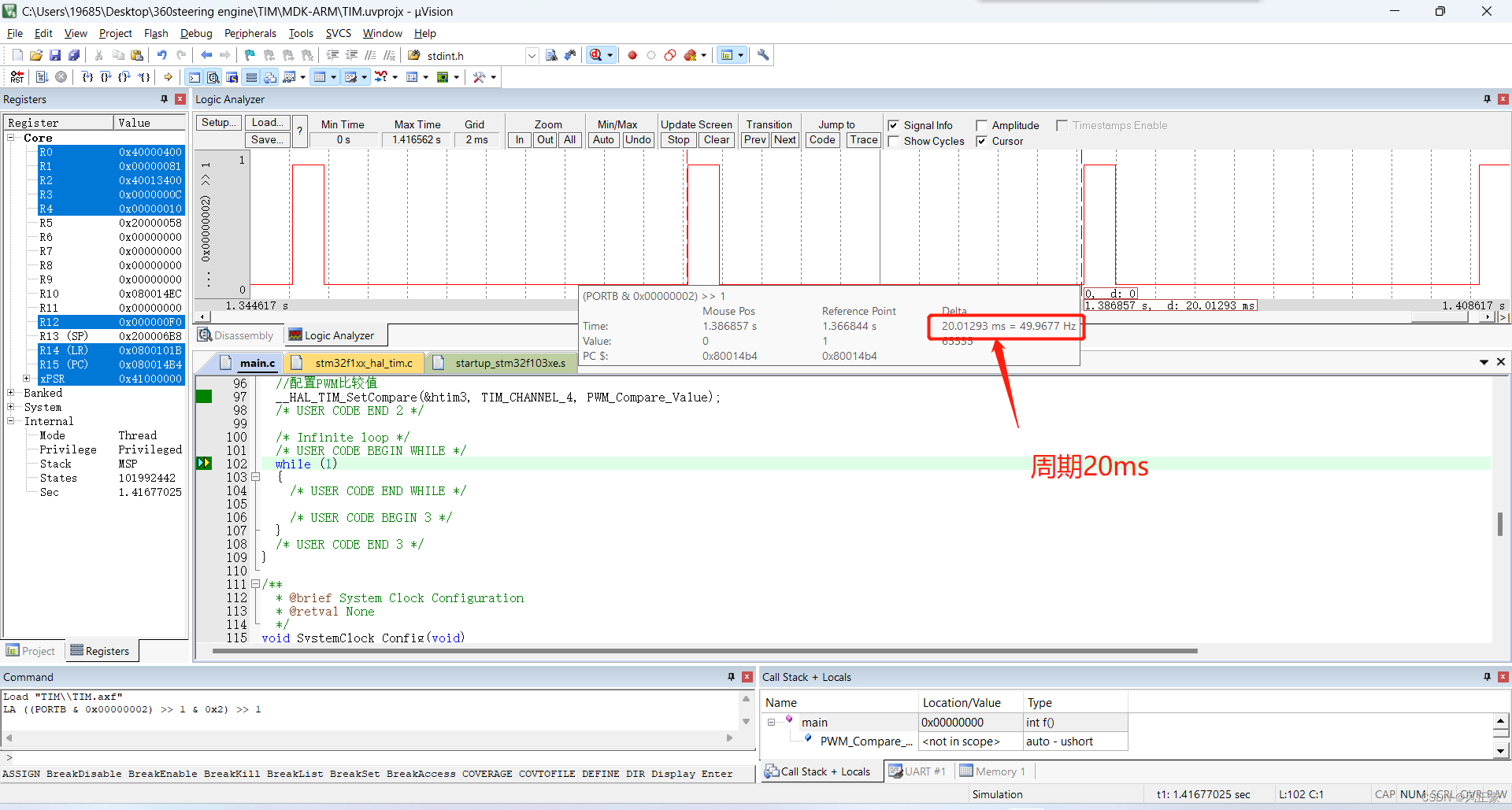
STM32F103CubeMX定时器
前言定时器作为最重要的内容之一,是每一位嵌入式软件工程师必备的能力。STM32F103的定时器是非常强大的。1,他可以用于精准定时,当成延时函数来使用。不过个人不建议这么使用,因为定时器很强大,这么搞太浪费了。如果想…...
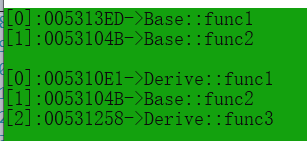
多态且原理
多态 文章目录多态多态的定义和条件协变(父类和子类的返回值类型不同)函数隐藏和虚函数重写的比较析构函数的重写关键字final和override抽象类多态的原理单继承和多继承的虚函数表单继承下的虚函数表多继承下的虚函数表多态的定义和条件 定义࿱…...
 创建动态库)
动态库(二) 创建动态库
文章目录创建动态库设计动态库ABI兼容动态符号的可见性示例控制符号可见性通过-fvisibility通过strip工具删除指定符号创建动态库 在Linux中创建动态库通过如下过程完成: gcc -fPIC -c first.c second.c gcc -shared first.o second.o -o libdynamiclib.so 按照Li…...

opencv加水印
本文介绍opencv给图片加水印的方法。 目录1、添加水印1.1、铺满1.2、在指定区域添加1.3、一比一铺满1、添加水印 添加水印的原理是调低两张图片的透明度,然后叠加起来。公式如下: dst src1 * opacity src2 * (1 - opacity) gamma; opacity是透明度&a…...
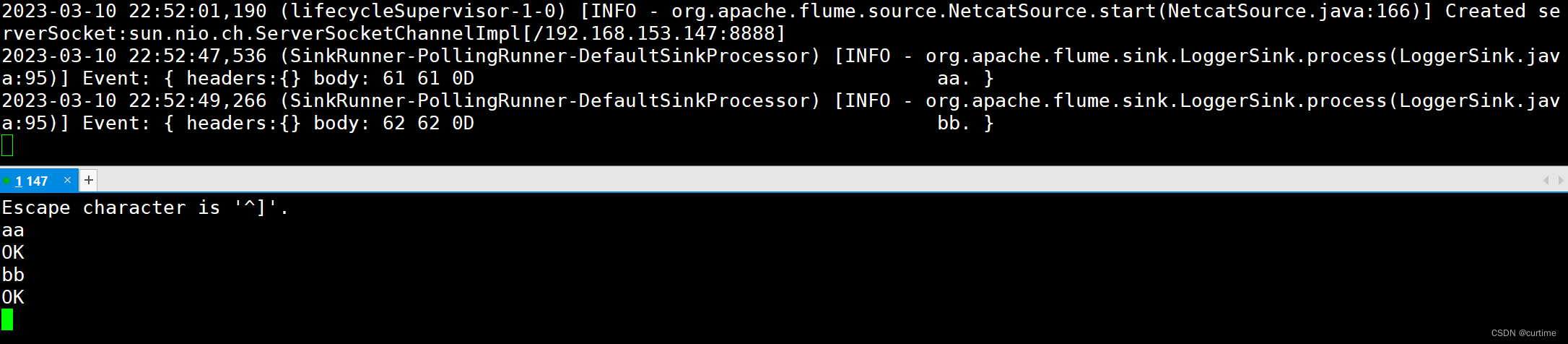
Flume基操
Flume概述 Flume 定义 Flume 是 Cloudera 提供的一个高可用的,高可靠的,分布式的海量日志采集、聚合和传输的系统。Flume 基于流式架构,灵活简单。 Flume最主要的作用就是,实时读取服务器本地磁盘的数据,将数据写入到…...
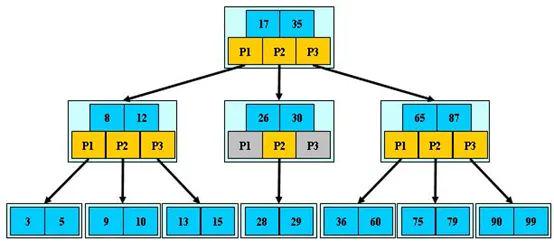
图文详解红黑树,还有谁不会?
前言在MySQL中,无论是Innodb还是MyIsam,都使用了B树作索引结构(这里不考虑hash等其他索引)。本文将从最普通的二叉查找树开始,逐步说明各种树解决的问题以及面临的新问题,从而说明MySQL为什么选择B树作为索引结构。目录一、二叉查…...
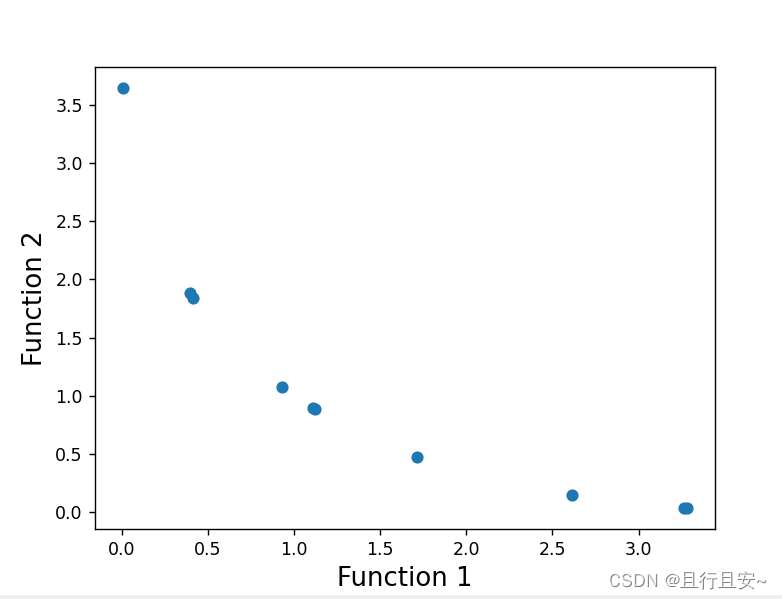
多目标遗传算法NSGA-II原理详解及算法实现
在接触学习多目标优化的问题上,经常会被提及到多目标遗传算法NSGA-II,网上也看到了很多人对该算法的总结,但真正讲解明白的以及配套用算法实现的文章很少,这里也对该算法进行一次详解与总结。会有侧重点的阐述,不会针对…...

Spark 键值对RDD的操作
键值对RDD(Pair RDD)是指每个RDD元素都是(key,value)键值对类型,是一种常见的RDD类型,可以应用于很多的应用场景。 一、 键值对RDD的创建 键值对RDD的创建主要有两种方式: &#x…...
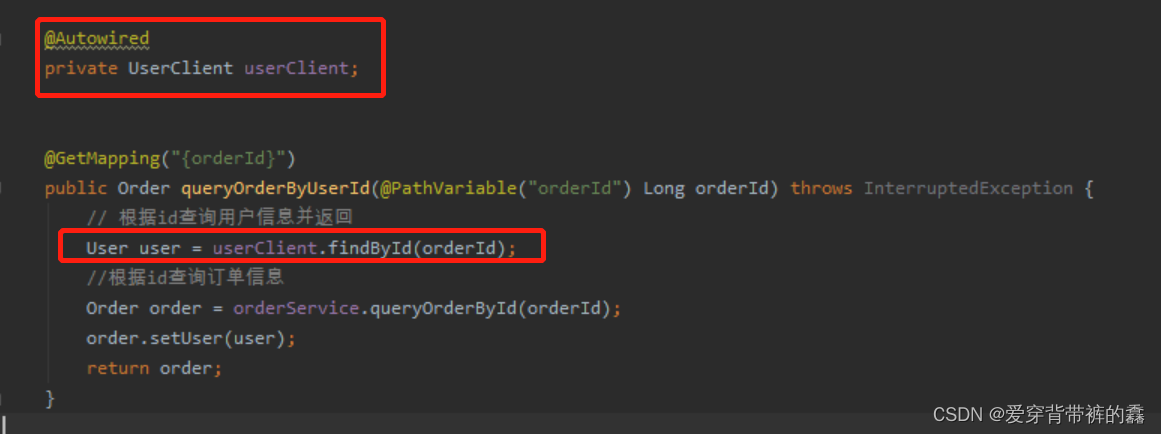
【SpringCloud】SpringCloud详解之Feign远程调用
目录前言SpringCloud Feign远程服务调用一.需求二.两个服务的yml配置和访问路径三.使用RestTemplate远程调用(order服务内编写)四.构建Feign(order服务内配置)五.自定义Feign配置(order服务内配置)六.Feign配置日志(oder服务内配置)七.Feign调优(order服务内配置)八.抽离Feign前…...
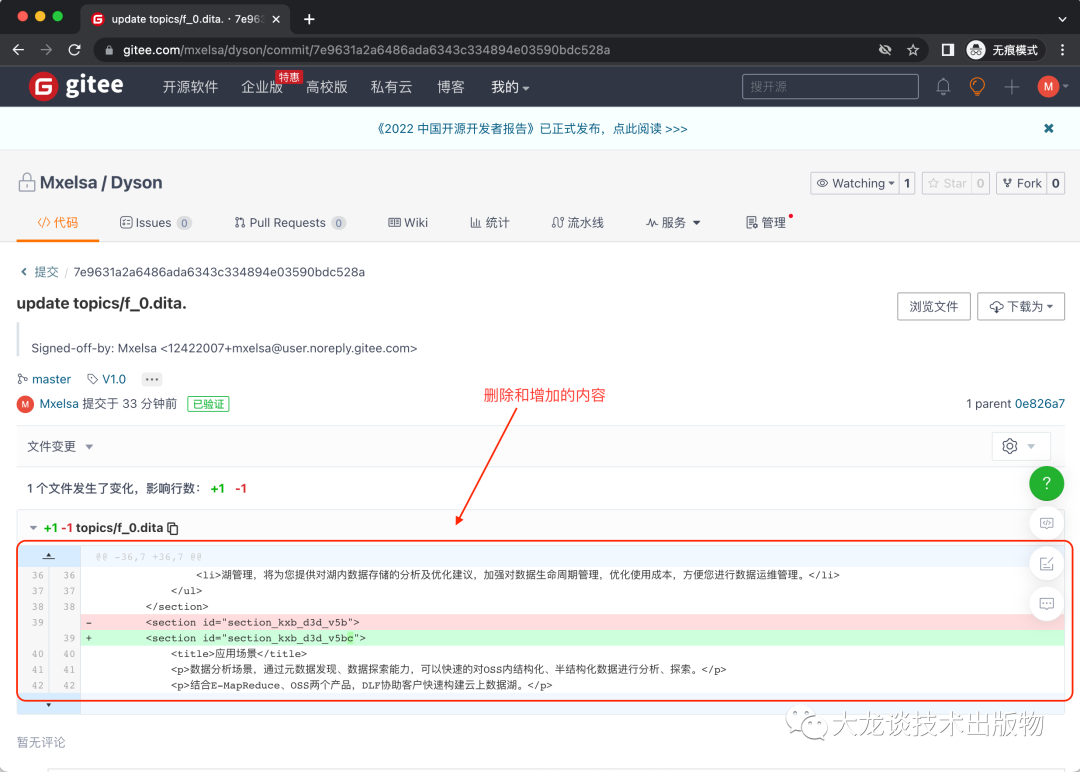
文档团队怎样使用GIT做版本管理
有不少小型文档团队想转结构化写作和发布,但是因为有限的IT技能和IT资源而受阻。本文为这样的小型文档团队而准备,描述怎样使用Git做内容的版本管理。 - 1 - 为什么需要版本管理 当一个团队进行协同创作内容时,有以下需要: 在对…...

【java】Java中-> 是什么意思?
先看一个例子 EventQueue.invokeLater(() -> {JFrame frame new ImageViewerFrame();frame.setTitle("ImageViewer");frame.setDefaultCloseOperation(JFrame.EXIT_ON_CLOSE);frame.setVisible(true);}); // 上面那一段可以看成如下: EventQueue.invokeLater(ne…...
网络类型部分实验
1.实验思路: 首先用DHCP 给四台PC配置上地址,配置成功后 其次底层IP地址的下发完成的同时,进行检测是否可以ping通 接着进行R1和R5之间使用PPP的PAP认证,R5为主认证方 主认证方ISP 被认证方R1 其次进行R2和R5使用PPP的CHAP认证&am…...
java教程--函数式接口--lambda表达式--方法引用
函数式接口 介绍 jdk8新特性,只有一个抽象方法的接口我们称之为函数接口。 FunctionalInterface JDK的函数式接口都加上了FunctionalInterface 注解进行标识。但是无论是否加上该注解只要接口中只有一个抽象方法,都是函数式接口。 如在Comparato…...
java——代理
什么是代理: 给目标对象一个代理对象,由代理对象控制着对目标对象的引用 为什么使用代理: ①:功能增强:通过代理业务对原有业务进行增强 ②:用户只能同行过代理对象间接访问目标对象,防止用…...

kubernetes中service探讨
文章目录序言kube-proxy代理模型userspace代理模型iptables代理模型ipvs代理模型修改代理模型Service资源类型ClusterIPNodePortLoadBalancerExternalName应用Service资源应用ClusterIP Service资源应用NodePort Service资源应用LoadBalancer Service资源外部IP序言 在Kuberne…...

Python3实现“美颜”功能
导语利用Python实现美颜。。。这是之前在GitHub上下载的一个项目。。。似乎有些日子了。。。所以暂时找不到原项目的链接了。。。今天抽空看了下它源代码的主要思想,似乎挺简单的。。。于是决定用Python3自己复现一下。。。T_T感觉还是挺有趣的。。。Just have a tr…...
【创建“待选项”按钮02计算坐标 Objective-C语言】
一、之前,我们已经把“待选项”按钮,创建好了,但是唯一的问题是,坐标都是一样的,所以都显示在一起了 1.下面,我们来设置一下,这些“待选项”按钮的坐标, 现在,“待选项”按钮的坐标,是不是都在同一个位置啊, 回忆一下,这个待选项按钮,是怎么生成的, 首先,是在…...

自组织( Self-organization),自组织临界性(Self-organized criticality)
文章目录1. 自组织概述原则历史按领域物理化学生物学2. 自组织临界性概述3. 自组织临界性的特征4. 自组织临界模型5. 自然界中的自组织临界6. 自组织临界性和优化7. 自组织临界性的控制7.1 方案7.2 应用1. 自组织 wiki: Self-organization 图 200 C 水热处理过程中微米级 Nb3O…...

DockerHub与私有镜像仓库在容器化中的应用与管理
哈喽,大家好,我是左手python! Docker Hub的应用与管理 Docker Hub的基本概念与使用方法 Docker Hub是Docker官方提供的一个公共镜像仓库,用户可以在其中找到各种操作系统、软件和应用的镜像。开发者可以通过Docker Hub轻松获取所…...

React Native在HarmonyOS 5.0阅读类应用开发中的实践
一、技术选型背景 随着HarmonyOS 5.0对Web兼容层的增强,React Native作为跨平台框架可通过重新编译ArkTS组件实现85%以上的代码复用率。阅读类应用具有UI复杂度低、数据流清晰的特点。 二、核心实现方案 1. 环境配置 (1)使用React Native…...
:爬虫完整流程)
Python爬虫(二):爬虫完整流程
爬虫完整流程详解(7大核心步骤实战技巧) 一、爬虫完整工作流程 以下是爬虫开发的完整流程,我将结合具体技术点和实战经验展开说明: 1. 目标分析与前期准备 网站技术分析: 使用浏览器开发者工具(F12&…...

Spring Boot面试题精选汇总
🤟致敬读者 🟩感谢阅读🟦笑口常开🟪生日快乐⬛早点睡觉 📘博主相关 🟧博主信息🟨博客首页🟫专栏推荐🟥活动信息 文章目录 Spring Boot面试题精选汇总⚙️ **一、核心概…...

全面解析各类VPN技术:GRE、IPsec、L2TP、SSL与MPLS VPN对比
目录 引言 VPN技术概述 GRE VPN 3.1 GRE封装结构 3.2 GRE的应用场景 GRE over IPsec 4.1 GRE over IPsec封装结构 4.2 为什么使用GRE over IPsec? IPsec VPN 5.1 IPsec传输模式(Transport Mode) 5.2 IPsec隧道模式(Tunne…...

C# 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

【Go语言基础【12】】指针:声明、取地址、解引用
文章目录 零、概述:指针 vs. 引用(类比其他语言)一、指针基础概念二、指针声明与初始化三、指针操作符1. &:取地址(拿到内存地址)2. *:解引用(拿到值) 四、空指针&am…...

Mysql8 忘记密码重置,以及问题解决
1.使用免密登录 找到配置MySQL文件,我的文件路径是/etc/mysql/my.cnf,有的人的是/etc/mysql/mysql.cnf 在里最后加入 skip-grant-tables重启MySQL服务 service mysql restartShutting down MySQL… SUCCESS! Starting MySQL… SUCCESS! 重启成功 2.登…...

【Linux】Linux 系统默认的目录及作用说明
博主介绍:✌全网粉丝23W,CSDN博客专家、Java领域优质创作者,掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域✌ 技术范围:SpringBoot、SpringCloud、Vue、SSM、HTML、Nodejs、Python、MySQL、PostgreSQL、大数据、物…...

Vue ③-生命周期 || 脚手架
生命周期 思考:什么时候可以发送初始化渲染请求?(越早越好) 什么时候可以开始操作dom?(至少dom得渲染出来) Vue生命周期: 一个Vue实例从 创建 到 销毁 的整个过程。 生命周期四个…...
