Matlab傅里叶谱方法求解一维波动方程
傅里叶谱方法求解基本偏微分方程—一维波动方程
一维波动方程
对于一根两端固定、没有受到任何外力的弦, 若只研究其中的一段, 在不太长的时间 里, 固定端来不及对这段弦产生影响, 则可以认为固定端是不存在的, 弦的长度为无限大。 这种无界 (−∞<x<∞)(-\infty<x<\infty)(−∞<x<∞) 弦的自由振动由式 (1)(1)(1) 描述。
∂2u∂t2=a2∂2u∂x2(1)\frac{\partial^2 u}{\partial t^2}=a^2 \frac{\partial^2 u}{\partial x^2} \tag{1} ∂t2∂2u=a2∂x2∂2u(1)
如果保证数值计算的区间足够大, 在一定时间内, 弦的振动范围始终没有超出计算区间 (或可以近似地这么认为), 那么就能够放心地使用周期性边界条件。取 a=1a=1a=1, 初始 条件为:
uut=0=2sech(x),∂u∂t∣t=0=0(2)u u_{t=0}=2 \operatorname{sech}(x),\left.\quad \frac{\partial u}{\partial t}\right|_{t=0}=0 \tag{2} uut=0=2sech(x),∂t∂ut=0=0(2)
在数学物理方法中, 无界弦的自由振动可由行波法求出解析解, 即达朗贝尔公式。 根据达朗贝尔公式, 从 t=0t=0t=0 开始, uuu 的初始状态 2sech(x)2 \operatorname{sech}(x)2sech(x) 将分裂为两个 sech 形的波, 分别向两边以速度 aaa 传播出去, 即正行波和反行波。下面用傅里叶缙方法求解无界弦 的自由振动问题, 并与达朗贝尔公式的预测进行比较。首先引入函数 vvv 对式 (1)(1)(1) 进行降阶:
{∂u∂t=v∂v∂t=a2∂2u∂x2(3)\left\{\begin{array}{l} \frac{\partial u}{\partial t}=v \\ \frac{\partial v}{\partial t}=a^2 \frac{\partial^2 u}{\partial x^2} \end{array}\right. \tag{3} {∂t∂u=v∂t∂v=a2∂x2∂2u(3)
对上式等号两边做傅里叶变换, 化为偏微分方程组:
{∂u^∂t=v^∂v^∂t=−a2k2u^(4)\left\{\begin{array}{l} \frac{\partial \hat{u}}{\partial t}=\hat{v} \\ \frac{\partial \hat{v}}{\partial t}=-a^2 k^2 \hat{u} \end{array}\right. \tag{4} {∂t∂u^=v^∂t∂v^=−a2k2u^(4)
这样就可以用 ode45 求解了, 详细代码如下:
主程序代码如下:
clear all; close all;L=80;N=256;
x=L/N*[-N/2:N/2-1];
k=(2*pi/L)*[0:N/2-1 -N/2:-1].';
% 初始条件
u=2*sech(x);ut=fft(u);
vt=zeros(1,N);uvt=[ut vt];
% 求解
a=1;t=0:0.5:20;
[t,uvtsol]=ode45('wave1D',t,uvt,[],N,k,a);
usol=ifft(uvtsol(:,1:N),[],2);
% 画图
p=[1 11 21 41];
for n=1:4subplot(5,2,n)plot(x,usol(p(n),:),'k','LineWidth',1.5),xlabel x,ylabel utitle(['t=' num2str(t(p(n)))]),axis([-L/2 L/2 0 2])
end
subplot(5,2,5:10)
waterfall(x,t,usol),view(10,45)
xlabel x,ylabel t,zlabel u,axis([-L/2 L/2 0 t(end) 0 2])文件 wave1D.m 代码如下:
function duvt=wave1D(t,uvt,dummy,N,k,a)
ut=uvt(1:N);vt=uvt(N+[1:N]);
duvt=[vt;-a^2*(k).^2.*ut];
end
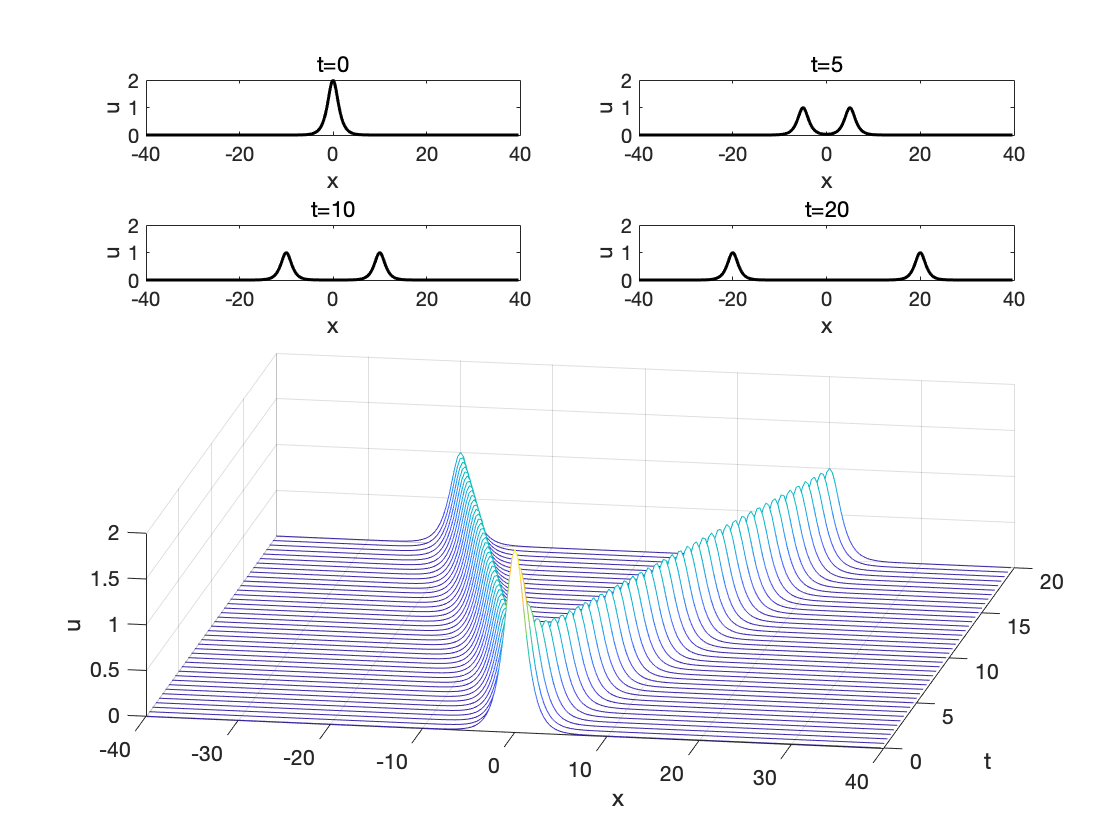
计算结果如图所示, 初始状态的波形分裂成两半, 并分别向 xxx 轴正方向和负方向 以速度 aaa 运动, 这和达朗贝尔公式给出的结论是一致的。
相关文章:

Matlab傅里叶谱方法求解一维波动方程
傅里叶谱方法求解基本偏微分方程—一维波动方程 一维波动方程 对于一根两端固定、没有受到任何外力的弦, 若只研究其中的一段, 在不太长的时间 里, 固定端来不及对这段弦产生影响, 则可以认为固定端是不存在的, 弦的长度为无限大。 这种无界 (−∞<x<∞)(-\infty<x&…...
函数典型例题)
py3中 collections.Counter()函数典型例题
文章目录py3中 collections 的常用STL**Counter()** 函数**defaultdict()** 函数**deque()** 函数**orderedDict()** 函数(缺例题)小结py3中 collections 的常用STL 对于这个工具包非常好用,尤其是其中的 Counter() 函数 使用次数颇为频繁&a…...

Linux部署达梦数据库超详细教程
陈老老老板🦸👨💻本文专栏:国产数据库-达梦数据库👨💻本文简述:本文讲一下达梦数据库的下载与安装教程(Linux版),超级详细。👨💻…...

ctfshow 每周大挑战 极限命令执行
《简单的命令执行题目》 这里感叹一下,g4佬是真好厉害,这次题目十分的难,嗯,对我这种菜鸡来说是这样的,想了一天,最后结束了,也还是没有想明白第五题的解法,我真是fw,到最…...

使用vue3,vite,less,flask,python从零开始学习硅谷外卖(16-40集)
严正声明! 重要的事情说一遍,本文章仅供分享,文章和代码都是开源的,严禁以此牟利,严禁侵犯尚硅谷原作视频的任何权益,我知道学习编程的人各种各样的心思都有,但这不是你对开源社区侵权的理由&am…...

坚持就是胜利
很多朋友,可能坚持了多年的同等学力申硕考试,依然没有通过。如果你感到困惑,感到迷茫,要坚信:坚持就能胜利。有很多人跟你一样,一直坚持在路上,没有停止脚步。 生活没有你想象的那么好ÿ…...
 或者转置 intrinsic (内参)矩阵的原因)
代码中出现转置 pose (c2w,外参矩阵) 或者转置 intrinsic (内参)矩阵的原因
在代码中见到 pose(c2w),intrinsic 矩阵的转置,觉得比较奇怪。 后来想了一下为什么。下面解释一下: 用 c2w 矩阵举例子。理论上,一个 c2w 左乘上 一个相机坐标系下的点 P的坐标,能够得到该点在…...

2023 年腾讯云服务器配置价格表出炉(2核2G/2核4G/4核8G/8核16G、16核32G)
腾讯云轻量应用服务器为轻量级的云服务器,使用门槛低,按套餐形式购买,轻量应用服务器套餐自带的公网带宽较大,4M、6M、7M、10M、14M及20M套餐可选,如果是云服务器CVM这个带宽价格就要贵很多了。 1、轻量应用服务器优惠…...
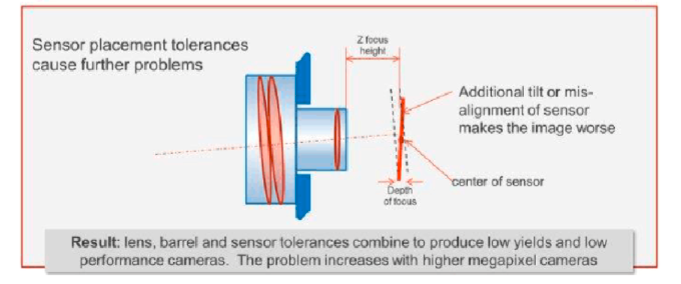
相机出图画面一半清晰,一半模糊的原因是什么?
1、问题背景:在做项目的过程中,有遇到过几次,出图后画面是一半清晰,一半模糊的现象,再重新对焦也是一样。但换了个镜头后就好了,这应该是镜头的质量问题,但导致镜头出现这种问题的具体原因是什么…...
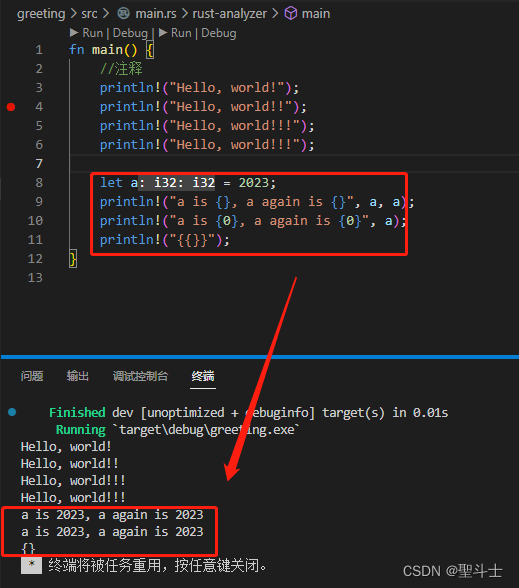
Rust学习入门--【4】Rust 输出到命令行
Rust 语言中的打印“函数” 学习新的编程语言时,大家都喜欢打印“Hello World”。 在Rust中怎样将字符串打印出来呢? Rust 输出文字的方式主要有两种:println!() 和 print!()。 “函数”差异说明: 这两个"函数"都是向…...

Vector刷写方案—vFlash工具介绍
我是穿拖鞋的汉子,魔都中坚持长期主义的工科男! 今天魔都天气是连阴雨,滴滴答答的下个不停,心情也跟着潮湿起来!老规矩分享一段喜欢的文字,避免成为高知识低文化的工程师: 即使在真正的困境里,也一直提示自己,每次自恋不得超过十分钟! 那些看似无法度过得困境,不是…...
》)
【阶段总结】《非结构化信息分析应用与实践(筹)》
《非结构化信息分析应用与实践(筹)》Part 1.知识储备一、机器学习 1.几种常见的有监督学习算法 2.几种常见的无监督学习算法 3.数据挖掘基础知识 30 问 二、神经网络与深度学习 1.MP神经网络模型(附实例代码讲解) 2.图解LST…...
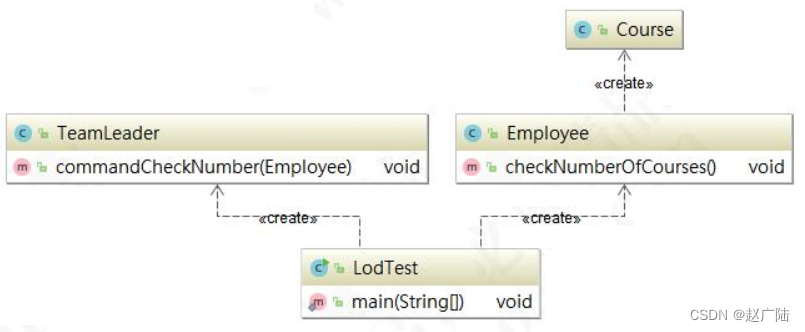
七大设计原则之迪米特法则应用
目录1 迪米特法则介绍2 迪米特法则应用1 迪米特法则介绍 迪米特原则(Law of Demeter LoD)是指一个对象应该对其他对象保持最少的了解,又叫最少知 道原则(Least Knowledge Principle,LKP),尽量降低类与类之…...

curl命令用法精简整理
目录1.GET请求1.1 形式1:1.2 形式2:2.POST请求2.1 无入参:2.2 form传参(文件):2.3 json入参:2.4 json文件入参:3.请求计时3.1 time命令(Linux):3.…...

Fluent Python 笔记 第 5 章 一等函数
在 Python 中,函数是一等对象。编程语言理论家把“一等对象”定义为满足下述条件的程 序实体: 在运行时创建能赋值给变量或数据结构中的元素 • 能作为参数传给函数能作为函数的返回结果 5.1 把函数视作对象 会用 map。 5.2 高阶函数 接受函数为参数࿰…...

卡尔曼滤波器与DSP实现
卡尔曼滤波器是利用系统状态方程,结合测量结果对系统状态进行进行最优估计的算法。本文介绍它的主要公式,并举例在C6000 DSP上实现。 推荐资料 KalmanFilter.NETUnderstanding Kalman Filters卡尔曼滤波与组合导航原理 “If you can’t explain it sim…...

引入QQ邮箱发送验证码进行安全校验
最近想给自己的项目在注册时加点安全校验,本想着使用短信验证码,奈何囊中羞涩只能退而求次改用QQ邮箱验证注册~ 一.需求分析 场景:用户输入自己的邮箱,点击获取验证码,后台会发送一封邮件到对应邮箱中。 分析&#x…...

【c++】数组
文章目录一维数组定义方式数组名案例案例1:元素逆置案例2:冒泡排序二维数组定义方式数组名案例:考试成绩统计数组特点: 1、每个数据元素放在一块连续的内存空间中; 2、数组中每个数据元素都是相同数据类型;…...
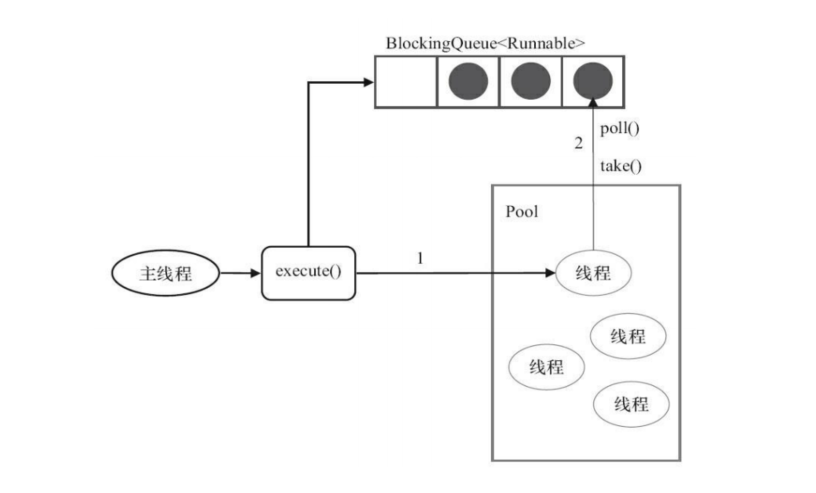
线程池的简单实现:Java线程池初学者必读指南
"作为一名Java开发者,是否曾经遇到过多线程并发的问题?线程数量过多时,会导致资源浪费,应用性能下降,甚至发生线程死锁的情况。那么,有没有一种方法可以有效地管理线程,避免这些问题呢&…...

【C#】[带格式的字符串] 复合格式设置字符串与使用 $ 的字符串内插 | 如何格式化输出字符串
复合格式输出 string name "Fred"; String.Format("Name {0}, hours {1:hh}", name, DateTime.Now);通过指定相同的参数说明符,多个格式项可以引用对象列表中的同一个元素。 例如,通过指定“0x{0:X} {0:E} {0:N}”等复合格式字符…...
)
椭圆曲线密码学(ECC)
一、ECC算法概述 椭圆曲线密码学(Elliptic Curve Cryptography)是基于椭圆曲线数学理论的公钥密码系统,由Neal Koblitz和Victor Miller在1985年独立提出。相比RSA,ECC在相同安全强度下密钥更短(256位ECC ≈ 3072位RSA…...

pam_env.so模块配置解析
在PAM(Pluggable Authentication Modules)配置中, /etc/pam.d/su 文件相关配置含义如下: 配置解析 auth required pam_env.so1. 字段分解 字段值说明模块类型auth认证类模块,负责验证用户身份&am…...

渲染学进阶内容——模型
最近在写模组的时候发现渲染器里面离不开模型的定义,在渲染的第二篇文章中简单的讲解了一下关于模型部分的内容,其实不管是方块还是方块实体,都离不开模型的内容 🧱 一、CubeListBuilder 功能解析 CubeListBuilder 是 Minecraft Java 版模型系统的核心构建器,用于动态创…...

Caliper 配置文件解析:fisco-bcos.json
config.yaml 文件 config.yaml 是 Caliper 的主配置文件,通常包含以下内容: test:name: fisco-bcos-test # 测试名称description: Performance test of FISCO-BCOS # 测试描述workers:type: local # 工作进程类型number: 5 # 工作进程数量monitor:type: - docker- pro…...

为什么要创建 Vue 实例
核心原因:Vue 需要一个「控制中心」来驱动整个应用 你可以把 Vue 实例想象成你应用的**「大脑」或「引擎」。它负责协调模板、数据、逻辑和行为,将它们变成一个活的、可交互的应用**。没有这个实例,你的代码只是一堆静态的 HTML、JavaScript 变量和函数,无法「活」起来。 …...

django blank 与 null的区别
1.blank blank控制表单验证时是否允许字段为空 2.null null控制数据库层面是否为空 但是,要注意以下几点: Django的表单验证与null无关:null参数控制的是数据库层面字段是否可以为NULL,而blank参数控制的是Django表单验证时字…...

Vue ③-生命周期 || 脚手架
生命周期 思考:什么时候可以发送初始化渲染请求?(越早越好) 什么时候可以开始操作dom?(至少dom得渲染出来) Vue生命周期: 一个Vue实例从 创建 到 销毁 的整个过程。 生命周期四个…...

阿里云Ubuntu 22.04 64位搭建Flask流程(亲测)
cd /home 进入home盘 安装虚拟环境: 1、安装virtualenv pip install virtualenv 2.创建新的虚拟环境: virtualenv myenv 3、激活虚拟环境(激活环境可以在当前环境下安装包) source myenv/bin/activate 此时,终端…...

【免费数据】2005-2019年我国272个地级市的旅游竞争力多指标数据(33个指标)
旅游业是一个城市的重要产业构成。旅游竞争力是一个城市竞争力的重要构成部分。一个城市的旅游竞争力反映了其在旅游市场竞争中的比较优势。 今日我们分享的是2005-2019年我国272个地级市的旅游竞争力多指标数据!该数据集源自2025年4月发表于《地理学报》的论文成果…...
EasyRTC音视频实时通话功能在WebRTC与智能硬件整合中的应用与优势
一、WebRTC与智能硬件整合趋势 随着物联网和实时通信需求的爆发式增长,WebRTC作为开源实时通信技术,为浏览器与移动应用提供免插件的音视频通信能力,在智能硬件领域的融合应用已成必然趋势。智能硬件不再局限于单一功能,对实时…...
