LeetCode - 42 接雨水
目录
题目来源
题目描述
示例
提示
题目解析
算法源码
题目来源
42. 接雨水 - 力扣(LeetCode)
题目描述
给定 n 个非负整数表示每个宽度为 1 的柱子的高度图,计算按此排列的柱子,下雨之后能接多少雨水。
示例1
输入:height = [0,1,0,2,1,0,1,3,2,1,2,1]
输出:6
解释:上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图,在这种情况下,可以接 6 个单位的雨水(蓝色部分表示雨水)。
示例2
输入:height = [4,2,0,3,2,5]
输出:9
提示
- n == height.length
- 1 <= n <= 2 * 10^4
- 0 <= height[i] <= 10^5
题目解析
本题要计算所有柱子的储水量之和,而这个和其实可以分解求解每一个柱子的储水量。
而一个柱子要想储存住水,则必然在其左边有一根高柱,在其右边也有一根高柱,因为这样才能形成“凹”,才能在中间的低柱子上存储住水。
并且,中间低柱子的储水量取决于,其左边“最高的”柱子,和其右边“最高的”柱子的较矮者,比如下图中:
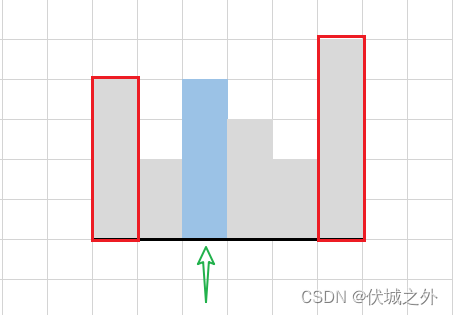
绿色箭头指向的低柱子的储水量取决于:其左边最高柱子,和其右边最高柱子的较矮者。
因此,本题其实是要我们求解每一根柱子的:
- 左边最高柱子高度
- 右边最高柱子高度
这个求解,可以使用动态规划来做:
我们假设第 i 根柱子的高度为 h[i],第 i 根柱子的左边最高柱子高度表示为left[ i ]
则第 i 根柱子的左边的最高柱子高度为:
left[ i ] = max( left[ i - 1 ], h[ i - 1 ] )
什么含义呢?
第 i 根柱子左边的最高柱子:
- 要么是 第 i - 1 根柱子,即h[ i - 1 ]
- 要么是 第 i - 1 根柱子的左边的最高柱子,即 left[ i - 1 ]
我们只要从左到右完成left数组的初始化即可。
同理,可得:
right[ i ] = max( right[ i + 1 ], h[ i + 1 ] )
此时需要从右往左完成right数组的初始化。
这样的话,第 i 根柱子的储水量
取决于其左边最高柱子,和其右边最高柱子的较矮者,即min(left[ i ], right[ i ])
第 i 根柱子的储水量val = min(left[ i ], right[ i ]) - h[ i ]
注意val最小为0,不能为负数。因此最终第 i 根柱子的储水量计算公式为:
max(0, min(left[ i ], right[ i ]) - h[i])
我们只要累加每根柱子的储水量即为题解。
Java算法源码
class Solution {public int trap(int[] h) {int n = h.length;// left[i] 表示 第 i 根柱子的左边的最高的柱子的高度int[] left = new int[n];for(int i=1; i<n; i++) {// 第 i 根柱子左边最高的柱子要么是h[i-1],即第i-1根柱子的高度,要么是left[i-1],即第i-1根柱子的左边的最高的柱子的高度left[i] = Math.max(left[i-1], h[i-1]);}// right[i] 表示 第 i 根柱子的右边的最高的柱子的高度int[] right = new int[n];for(int i=n-2; i>=0; i--) {// 第 i 根柱子右边最高的柱子要么是h[i+1],即第i+1根柱子的高度,要么是right[i+1],即第i+1根柱子的右边的最高的柱子的高度right[i] = Math.max(right[i+1], h[i+1]);}int ans = 0;for(int i=1; i<n-1; i++) {// 第i根柱子最多能蓄水的量,取决于其左边最高的柱子和右边最高的柱子的较矮的那个,且较矮的那根柱子 - 第i根柱子的高度就是第i根柱子的蓄水量,注意蓄水量最少为0ans += Math.max(0, Math.min(left[i], right[i]) - h[i]);}return ans;}
}
JS算法源码
/*** @param {number[]} height* @return {number}*/
var trap = function(h) {const n = h.length// left[i] 表示 第 i 根柱子的左边的最高的柱子的高度const left = new Array(n).fill(0)for(let i=1; i<n; i++) {// 第 i 根柱子左边最高的柱子要么是h[i-1],即第i-1根柱子的高度,要么是left[i-1],即第i-1根柱子的左边的最高的柱子的高度left[i] = Math.max(left[i-1], h[i-1])}// right[i] 表示 第 i 根柱子的右边的最高的柱子的高度const right = new Array(n).fill(0)for(let i=n-2; i>=0; i--) {// 第 i 根柱子右边最高的柱子要么是h[i+1],即第i+1根柱子的高度,要么是right[i+1],即第i+1根柱子的右边的最高的柱子的高度right[i] = Math.max(right[i+1], h[i+1])}let ans = 0for(let i=1; i<n-1; i++) {// 第i根柱子最多能蓄水的量,取决于其左边最高的柱子和右边最高的柱子的较矮的那个,且较矮的那根柱子 - 第i根柱子的高度就是第i根柱子的蓄水量,注意蓄水量最少为0ans += Math.max(0, Math.min(left[i], right[i]) - h[i])}return ans
};
Python算法源码
class Solution(object):def trap(self, h):""":type height: List[int]:rtype: int"""n = len(h)# left[i] 表示 第 i 根柱子的左边的最高的柱子的高度left = [0]*nfor i in range(1, n):# 第 i 根柱子左边最高的柱子要么是h[i-1],即第i-1根柱子的高度,要么是left[i-1],即第i-1根柱子的左边的最高的柱子的高度left[i] = max(left[i-1], h[i-1])# right[i] 表示 第 i 根柱子的右边的最高的柱子的高度right = [0]*nfor i in range(n-2,0,-1):# 第 i 根柱子右边最高的柱子要么是h[i+1],即第i+1根柱子的高度,要么是right[i+1],即第i+1根柱子的右边的最高的柱子的高度right[i] = max(right[i+1], h[i+1])ans = 0for i in range(1, n-1):# 第i根柱子最多能蓄水的量,取决于其左边最高的柱子和右边最高的柱子的较矮的那个,且较矮的那根柱子 - 第i根柱子的高度就是第i根柱子的蓄水量,注意蓄水量最少为0ans += max(0, min(left[i], right[i]) - h[i])return ans
相关文章:

LeetCode - 42 接雨水
目录 题目来源 题目描述 示例 提示 题目解析 算法源码 题目来源 42. 接雨水 - 力扣(LeetCode) 题目描述 给定 n 个非负整数表示每个宽度为 1 的柱子的高度图,计算按此排列的柱子,下雨之后能接多少雨水。 示例1 输入&…...
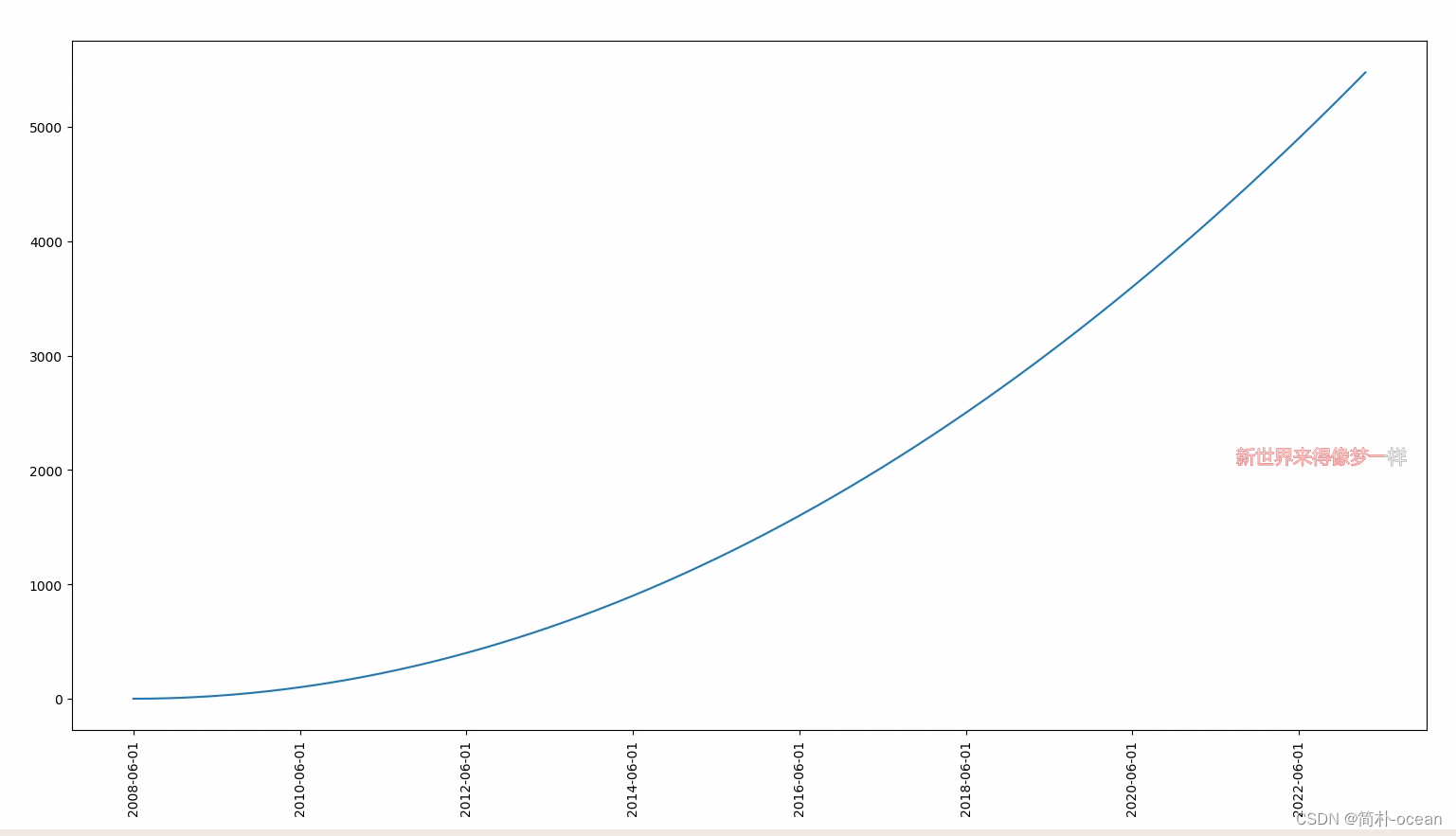
python --生成时间序列,作为横轴的标签。时间跨越2008-2022年,生成每年的6-10月的第一天作为时间序列
python 生成制定的时间序列作为绘图时x轴的标签 问题需求 在绘图时,需要对于x轴的标签进行专门的设置,整体时间跨越2008年-2022年,将每年的6-10月的第一天生成一条时间序列,绘制成图。 解决思路 对于时间序列的生成࿰…...

【Unity VR开发】结合VRTK4.0:创建一个按钮(Togglr Button)
语录: 有人感激过你的善良吗,貌似他们只会得寸进尺。 前言: Toggle按钮是提供简单空间 UI 选项的另一种方式,在该选项中,按钮将保持其状态,直到再次单击它。这允许按钮处于激活状态或停用状态的情况&#…...
lottie-miniprogram在taro+vue的小程序中怎么使用
把一个json的动图展示在页面上。使用的是插件lottie-miniprogramhttps://blog.csdn.net/qq_33769914/article/details/128705922之前介绍过。但是发现使用在taro使用的时候他会报错。那可能是因为我们 wx.createSelectorQuery().select(#canvas).node(res > {console.log(re…...
C++回顾(二十二)—— stack容器 与 queue容器
22.1 stack容器 (1) stack容器简介 stack是堆栈容器,是一种“先进后出”的容器。stack是简单地装饰deque容器而成为另外的一种容器。添加头文件:#include <stack> (2)stack对象的默认构造 stack…...
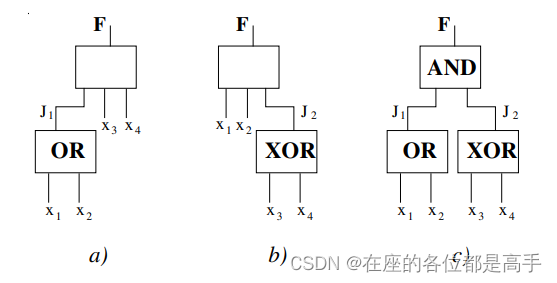
逻辑优化基础-disjoint support decomposition
先遣兵 在了解 disjoint support decomposition 之前,先学习两个基本的概念。 disjoint 数学含义上的两个集合交集,所谓非相交,即交集为空集。 A∩BC⊘A \cap B C \oslash A∩BC⊘ support 逻辑综合中的 supportsupportsupport 概念是…...

保姆级使用PyTorch训练与评估自己的DaViT网络教程
文章目录前言0. 环境搭建&快速开始1. 数据集制作1.1 标签文件制作1.2 数据集划分1.3 数据集信息文件制作2. 修改参数文件3. 训练4. 评估5. 其他教程前言 项目地址:https://github.com/Fafa-DL/Awesome-Backbones 操作教程:https://www.bilibili.co…...

Java8新特性:Stream流处理使用总结
一. 概述 Stream流是Java8推出的、批量处理数据集合的新特性,在java.util.stream包下。结合着Java8同期推出的另一项新技术:行为参数化(包括函数式接口、Lambda表达式、方法引用等),Java语言吸收了函数式编程的语法特…...

Java基准测试工具JMH高级使用
去年,我们写过一篇关于JMH的入门使用的文章:Java基准测试工具JMH使用,今天我们再来聊一下关于JMH的高阶使用。主要我们会围绕着以下几点来讲: 对称并发测试非对称并发测试阻塞并发测试Map并发测试 关键词 State 在很多时候我们…...
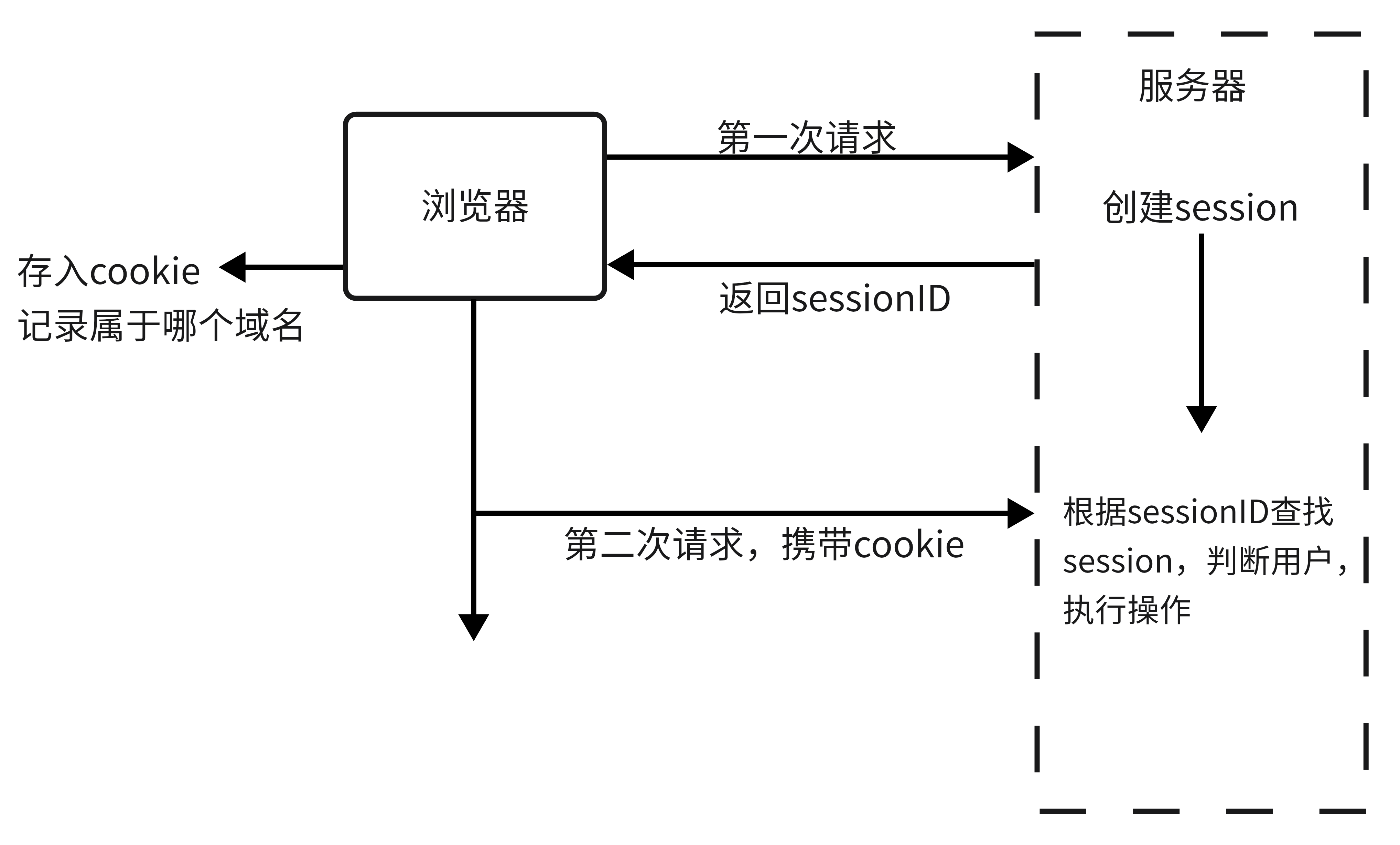
问心 | 再看token、session和cookie
什么是cookie HTTP Cookie(也叫 Web Cookie或浏览器 Cookie)是服务器发送到用户浏览器并保存在本地的一小块数据,它会在浏览器下次向同一服务器再发起请求时被携带并发送到服务器上。 什么是session Session 代表着服务器和客户端一次会话…...

Ubuntu 安装 CUDA and Cudnn
文章目录0 查看 nvidia驱动版本1 下载Cuda2 下载cudnn参考:0 查看 nvidia驱动版本 nvidia-smi1 下载Cuda 安装之前先安装 gcc g gdb 官方:https://developer.nvidia.com/cuda-toolkit-archive,与驱动版本进行对应,我这里是12.0…...
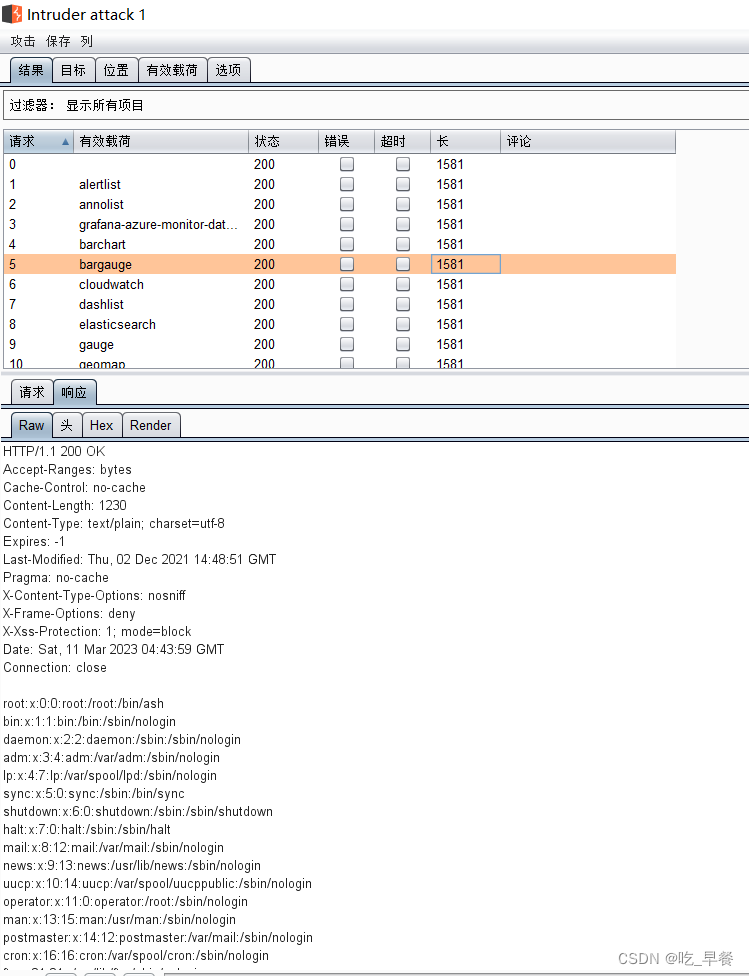
【漏洞复现】Grafana任意文件读取(CVE-2021-43798)
docker环境搭建 #进入环境 cd vulhub/grafana/CVE-2021-43798#启动环境,这个过程可能会有点慢,保持网络通畅 docker-compose up -d#查看环境 docker-compose ps直接访问虚拟机 IP地址:3000 目录遍历原理 目录遍历原理:攻击者可以通过将包含…...

磨金石教育摄影技能干货分享|春之旅拍
春天来一次短暂的旅行,你会选择哪里呢?春天的照片又该如何拍呢?看看下面的照片,或许能给你答案。照片的构图很巧妙,画面被分成两部分,一半湖泊,一半绿色树林。分开这些的是一条斜向的公路&#…...
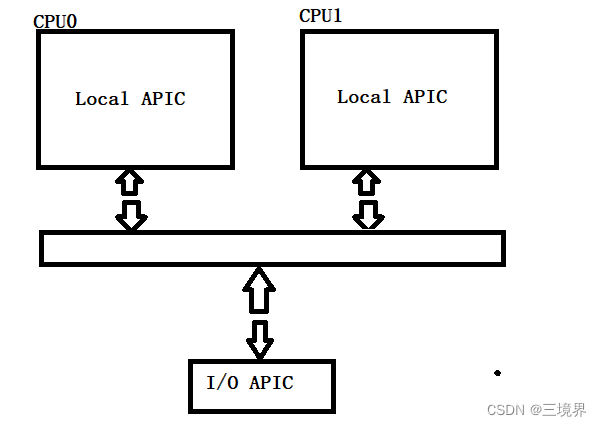
中断以及 PIC可编程中断控制器
1 中断分为同步中断(中断)和异步中断(异常) 1.1 中断和异常的不同 中断由IO设备和定时器产生,用户的一次按键会引起中断。异步。 异常一般由程序错误产生或者由内核必须处理的异常条件产生。同步。缺页异常ÿ…...
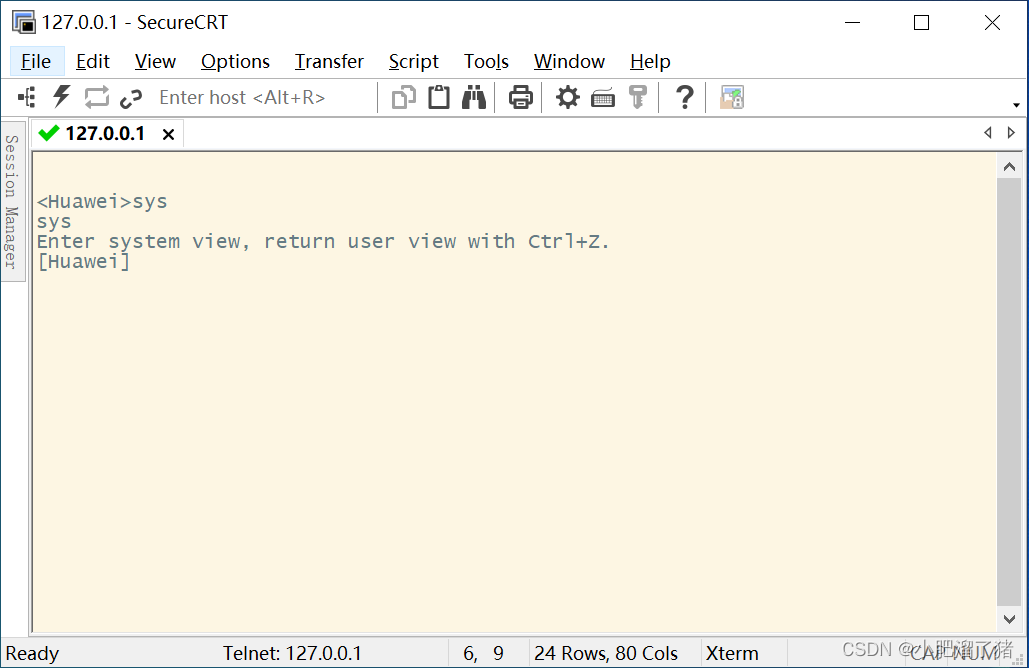
SecureCRT 安装并绑定ENSP设备终端
软件下载链接链接:https://pan.baidu.com/s/1WFxmQgaO9bIiUTwBLSR4OA?pwd2023 提取码:2023 CRT安装:软件可以从上面链接进行下载,下载完成后解压如下:首先双击运行scrt-x64.8.5.4 软件,进行安装点击NEXT选…...

ESP32设备驱动-TCS3200颜色传感器驱动
TCS3200颜色传感器驱动 1、TCS3200介绍 TCS3200 和 TCS3210 可编程彩色光频率转换器在单个单片 CMOS 集成电路上结合了可配置的硅光电二极管和电流频率转换器。 输出是方波(50% 占空比),其频率与光强度(辐照度)成正比。 满量程输出频率可以通过两个控制输入引脚按三个预…...
< JavaScript小技巧:Array构造函数妙用 >
文章目录👉 Array构造函数 - 基本概念👉 Array函数技巧用法1. Array.of()2. Array.from()3. Array.reduce()4. (Array | String).includes()5. Array.at()6. Array.flat()7. Array.findIndex()📃 参考文献往期内容 💨今天这篇文章…...
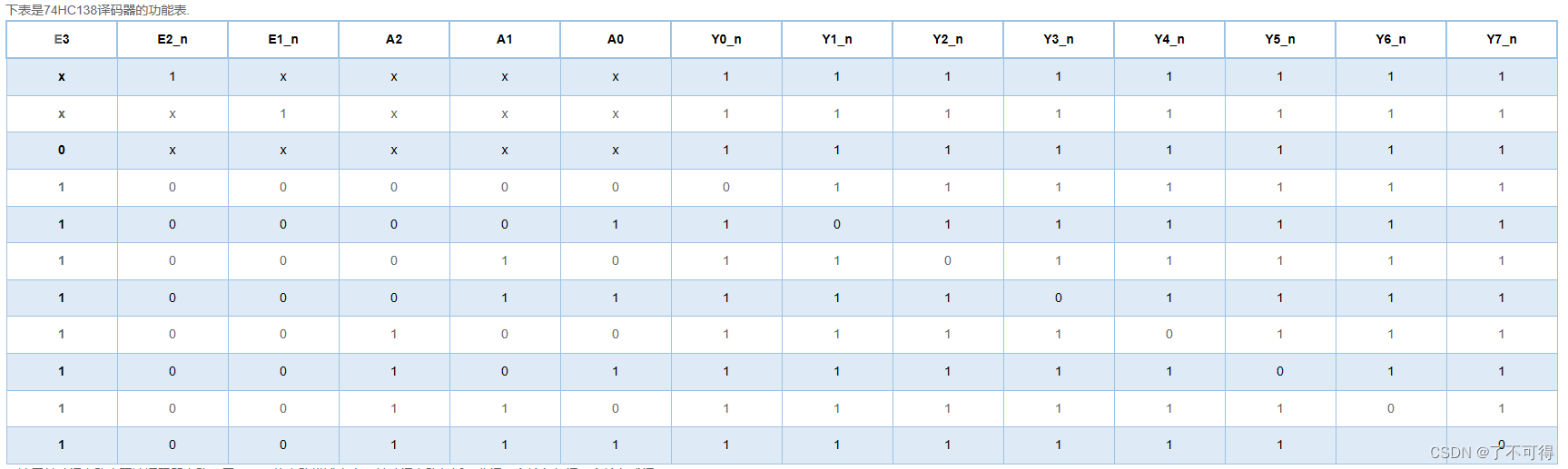
【17】组合逻辑 - VL17/VL19/VL20 用3-8译码器 或 4选1多路选择器 实现逻辑函数
VL17 用3-8译码器实现全减器 【本题我的也是绝境】 因为把握到了题目的本质要求【用3-8译码器】来实现全减器。 其实我对全减器也是不大清楚,但是仿照对全加器的理解,全减器就是低位不够减来自低位的借位 和 本单元位不够减向后面一位索要的借位。如此而已,也没有很难理解…...

2023年全国最新二级建造师精选真题及答案19
百分百题库提供二级建造师考试试题、二建考试预测题、二级建造师考试真题、二建证考试题库等,提供在线做题刷题,在线模拟考试,助你考试轻松过关。 37.下列纠纷中,属于劳动争议范围的有()。 A.因劳动保护发生的纠纷 B.家庭与家政…...
Java中的 this 和 super
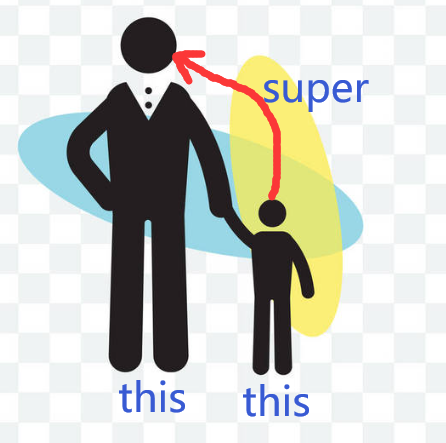
1 this 关键字 1.1 this 访问本类属性 this 代表对当前对象的一个引用 所谓当前对象,指的是调用当前类中方法或属性的那个对象this只能在方法内部使用,表示对“调用方法的那个对象”的引用this.属性名,表示本对象自己的属性 当对象的属性和…...

多云管理“拦路虎”:深入解析网络互联、身份同步与成本可视化的技术复杂度
一、引言:多云环境的技术复杂性本质 企业采用多云策略已从技术选型升维至生存刚需。当业务系统分散部署在多个云平台时,基础设施的技术债呈现指数级积累。网络连接、身份认证、成本管理这三大核心挑战相互嵌套:跨云网络构建数据…...

设计模式和设计原则回顾
设计模式和设计原则回顾 23种设计模式是设计原则的完美体现,设计原则设计原则是设计模式的理论基石, 设计模式 在经典的设计模式分类中(如《设计模式:可复用面向对象软件的基础》一书中),总共有23种设计模式,分为三大类: 一、创建型模式(5种) 1. 单例模式(Sing…...

在rocky linux 9.5上在线安装 docker
前面是指南,后面是日志 sudo dnf config-manager --add-repo https://download.docker.com/linux/centos/docker-ce.repo sudo dnf install docker-ce docker-ce-cli containerd.io -y docker version sudo systemctl start docker sudo systemctl status docker …...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院挂号小程序
一、开发准备 环境搭建: 安装DevEco Studio 3.0或更高版本配置HarmonyOS SDK申请开发者账号 项目创建: File > New > Create Project > Application (选择"Empty Ability") 二、核心功能实现 1. 医院科室展示 /…...

基础测试工具使用经验
背景 vtune,perf, nsight system等基础测试工具,都是用过的,但是没有记录,都逐渐忘了。所以写这篇博客总结记录一下,只要以后发现新的用法,就记得来编辑补充一下 perf 比较基础的用法: 先改这…...

从零开始打造 OpenSTLinux 6.6 Yocto 系统(基于STM32CubeMX)(九)
设备树移植 和uboot设备树修改的内容同步到kernel将设备树stm32mp157d-stm32mp157daa1-mx.dts复制到内核源码目录下 源码修改及编译 修改arch/arm/boot/dts/st/Makefile,新增设备树编译 stm32mp157f-ev1-m4-examples.dtb \stm32mp157d-stm32mp157daa1-mx.dtb修改…...

Spring Boot面试题精选汇总
🤟致敬读者 🟩感谢阅读🟦笑口常开🟪生日快乐⬛早点睡觉 📘博主相关 🟧博主信息🟨博客首页🟫专栏推荐🟥活动信息 文章目录 Spring Boot面试题精选汇总⚙️ **一、核心概…...

C++ Visual Studio 2017厂商给的源码没有.sln文件 易兆微芯片下载工具加开机动画下载。
1.先用Visual Studio 2017打开Yichip YC31xx loader.vcxproj,再用Visual Studio 2022打开。再保侟就有.sln文件了。 易兆微芯片下载工具加开机动画下载 ExtraDownloadFile1Info.\logo.bin|0|0|10D2000|0 MFC应用兼容CMD 在BOOL CYichipYC31xxloaderDlg::OnIni…...

CMake控制VS2022项目文件分组
我们可以通过 CMake 控制源文件的组织结构,使它们在 VS 解决方案资源管理器中以“组”(Filter)的形式进行分类展示。 🎯 目标 通过 CMake 脚本将 .cpp、.h 等源文件分组显示在 Visual Studio 2022 的解决方案资源管理器中。 ✅ 支持的方法汇总(共4种) 方法描述是否推荐…...

算法岗面试经验分享-大模型篇
文章目录 A 基础语言模型A.1 TransformerA.2 Bert B 大语言模型结构B.1 GPTB.2 LLamaB.3 ChatGLMB.4 Qwen C 大语言模型微调C.1 Fine-tuningC.2 Adapter-tuningC.3 Prefix-tuningC.4 P-tuningC.5 LoRA A 基础语言模型 A.1 Transformer (1)资源 论文&a…...
